基于预防性维修的汽车质保服务策略优化
2018-09-06董方岐
门 峰,董方岐
(1.中国汽车技术研究中心有限公司,天津 300300 2.天津大学 管理与经济学部,天津 300072)
汽车质保服务属于典型的二维产品质保策略,其质保期通过使用时间与使用里程的组合进行确定,如我国常见的汽车质保服务为3年或6万km,以先到者为准[1-2]。在汽车质保服务中,厂商必须为处于质保期内发生故障的汽车提供维修服务,或者赔偿产品故障给消费者带来的损失[3]。随着汽车市场竞争的逐渐加剧,汽车质保服务逐渐成为汽车制造商提高产品服务质量与增强产品市场竞争力的重要战略组成部分[4]。在汽车质保中维修策略的优化对于降低产品保证服务成本,提高消费者满意度及制造商利润具有重要作用,如合理的维修策略优化能使产品保证服务成本降低5%~20%[5]。
目前常见的维修策略主要分为修正性维修和预防性维修策略两类,其中修正性维修是指在产品出现故障后进行修复或更换等处理[6]。预防性维修是在产品未出现故障时采取的一种计划性维修策略,以降低产品故障率的发生,提高产品使用可靠性水平。目前,预防性维修作为一种能够有效提高产品可靠性水平、降低产品保证期望服务成本的维修策略目前得到了广泛的研究[7-8]。非完美维修是将产品可靠性恢复到初始状态和当前状态之间的一个水准,该方法由于费用合理而更多地被采用。为了衡量非完美预防维修对产品可靠性的影响效果,专家和学者通常采用产品役龄比例减少和故障率降低两种方式对其进行建模[9-10]。
当前预防性维修策略在产品质保中的应用研究以固定时间间隔的定期维修为主,如CHUN[11]将预防性维修策略与产品质保策略相结合,对免费质保服务中预防性维修的固定时间间隔进行了优化研究。YEH等[12]对可修产品的定期预防性维修策略进行了优化研究,通过算法研究指出存在唯一的最优时间间隔,使产品质保服务成本最小化。文献[4]在假定质保期内产品采用最小维修策略的前提下,在二维基本保证期和延伸保证期内,构建了基于固定时间的预防性维修策略,并以整体保证期内期望成本最小化为目标,对预防性维修的固定时间价格和维修程度进行了优化研究。徐德凯等[13-14]针对二维延伸质保服务,构建了基于可靠性水平的非定期预防性维修策略,并以质保期内整体期望成本最小化为目标,对预防性维修进行了优化研究,该策略可以有效降低质保服务成本。戴安舒等[15]针对以汽车产品为主的二维产品质保服务,根据产品使用率的大小将消费者分为两类,同样以质保期内期望成本最小化为目标,首次为消费者构建了基于固定时间和固定里程组合的预防性维修策略,有效降低了二维质保服务的期望成本。综上所述,在汽车二维质保服务内,设计和优化预防性维修策略可以有效降低质保期内的期望维修成本,进而提高制造商的利润。
当前产品质保中关于预防性维修策略的研究以固定时间间隔为主,在汽车质保服务中,由于使用时间与使用里程共同影响着汽车故障率函数,设计和优化基于固定使用里程的预防性维修策略,能够作为定期预防性维修策略的有效补充,对汽车质保服务策略的优化进行有效指导。基于以上分析,笔者首次提出了以固定使用里程为间隔的预防性维修策略,并将其在不同汽车服务质保期组合中的应用进行了优化研究,最后通过算例对比了采用定期预防性维修策略与基于固定使用里程预防性维修策略的期望成本大小,对所构建维修策略的有效性和适用性进行了有效分析。
1 模型构建
1.1 基本假设
(1)汽车属于可修产品,汽车故障率在整个质保期内随着使用时间和使用里程的增加而增加。
(2) 不同消费者的汽车产品使用率不同,而同一个消费者的使用习惯不变,在整个汽车质保期内的使用率维持不变。
(3)汽车在质保期内失效采用最小维修,最小维修与预防性维修的时间可忽略不计。
1.2 汽车故障率函数与预防性维修模型
在质保期内,消费者的产品使用率是影响预防性维修策略优化设计的关键因素[16-17]。目前已有较多专家和学者对汽车质保中的故障率函数拟合进行了研究,主要分为: 二元失效分布法(bivariate)、复合标度法(composite)和边际方法(marginal approach)3种[18-19],笔者沿用边际分析方法对汽车产品故障率进行有效建模。 设x、u分别为汽车的使用时间和累计使用量,对于给定的汽车产品使用率r,有u=rx,设g(r)、G(r)分别为消费者产品使用率的密度函数和累计分布函数,可通过历史数据分析拟合获取。根据ISKANDAR等的研究成果[20],汽车产品在寿命时间为x时的故障率函数可表示为x、r的多项式函数:
h0(x|r)=θ0+θ1r+(θ2+θ3r)x
(1)
其中,参数θ0、θ1、θ2、θ3均大于0,可以根据汽车历史维修数据、质保索赔数据通过多元线性回归的方法估计求得。对于所有故障都采用最小维修方式且维修时间可忽略不计,在整个汽车质保期内产品失效服从非均匀泊松分布,且强度函数服从λ0(x|r)=h0(x|r)。这里沿用文献[21]中产品役龄比例减少模型对预防性维修进行了有效建模。设τj为基于里程的第j次预防性维修的维修时间,并令τ0=0。与以往研究不同,基于固定使用里程的预防性维修策略对于所有消费者而言,每当汽车使用里程到达某一数值时便对汽车进行预防性维修。设预防性维修的固定里程间隔为S,对于汽车产品使用率为r的消费者而言,其预防性维修的时间间隔为:
(2)
由此可见,不同消费者的预防性维修时间间隔不同,与消费者的产品使用率直接相关。在预防性维修中第j次预防性维修仅对在第j-1次预防性维修到第j次预防性维修之间降低的产品故障率进行了弥补,产品在第j次预防性维修后的虚拟寿命为:
vj=vj-1+δ(m)(τj-τj-1)
(3)
式中:vj为第j次预防性维修之后汽车的虚拟寿命;τj为第j次预防性维修的时间;m为预防性维修的程度,m=0,1,2,…,M;δ(m)为第m类预防性维修的虚拟寿命降低因子。m=0表示没有进行预防性维修,此时δ(0)=1;m=M表示完美的预防性维修,此时δ(M)=0。笔者取δ(m)=(1+m)×e-m。通过迭代计算可以得出:
vj=v0+δ(m)(τj-τ0)=
(4)
其中,v0为汽车的初始实际使用寿命,通常取其值为0。
1.3 汽车质保维修成本优化建模
设(W,U)为汽车产品的二维质保期组合,W为质保时间,U为质保里程,(S,m)为拟采用的预防性维修固定使用里程间隔与维修程度组合,Cpm(m)为第m类预防性维修成本,Cmin为最小维修成本,Q1=U/W,是汽车质保里程与时间之比,rmax、rmin分别为消费者最高使用率与最低使用率。
(1)当消费者产品使用率rmax>r>Q1时,消费者在整个质保期内的预防性维修次数和产品的修正性维修成本期望分别为:
npm1=[U/S]
(5)
(6)
其中,[]为取整符号。
产品的预防性维修成本期望为:
ECpm1=[U/S]×Cpm(m)
(7)
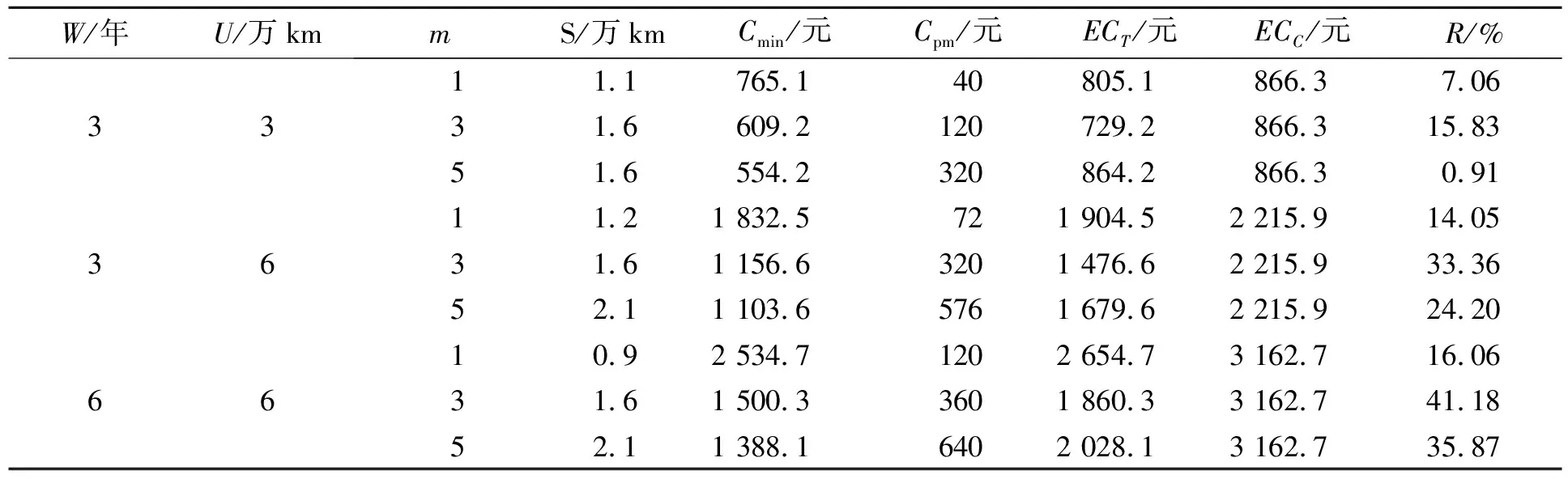
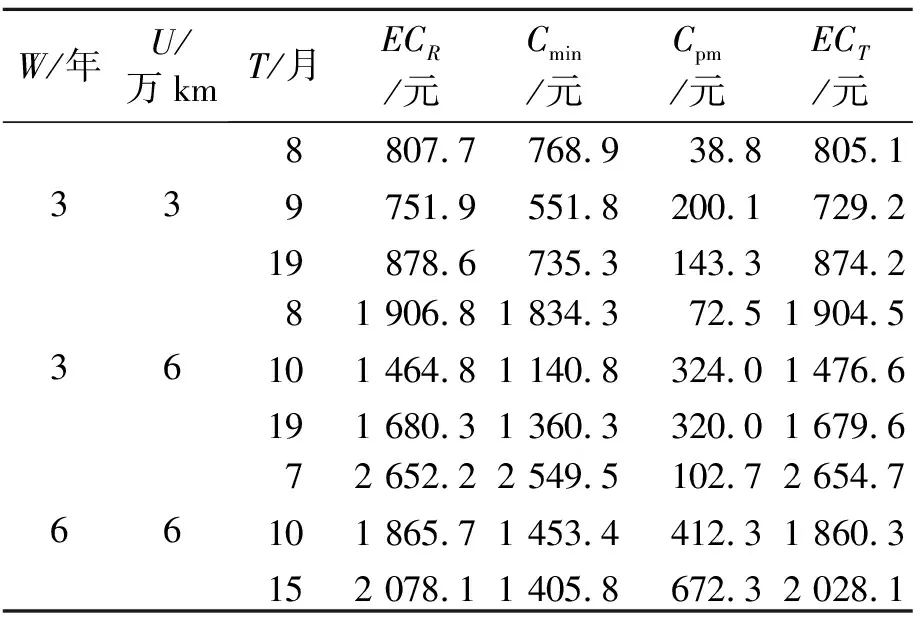
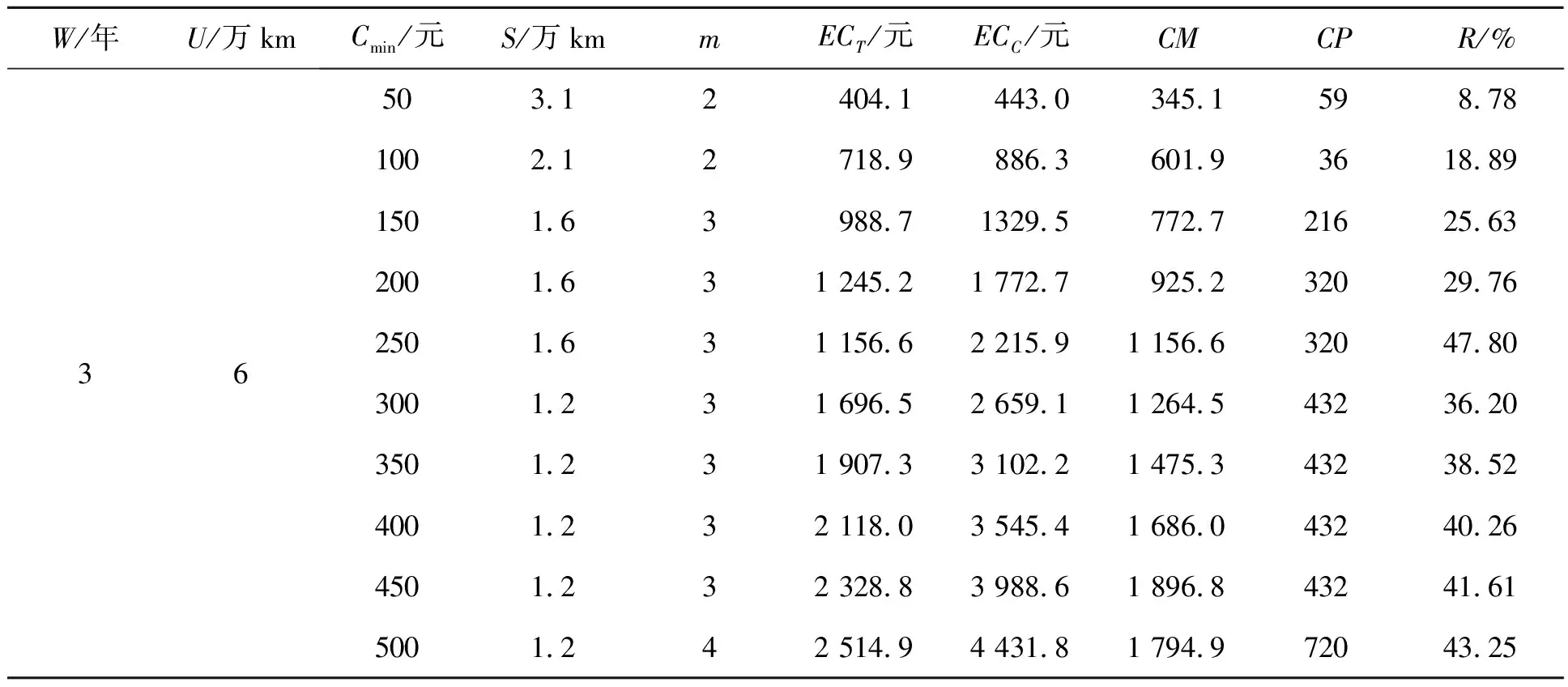
(2)当消费者产品使用率rmin npm2=[Wr/S] (8) 产品的预防性维修成本期望为: ECpm2=[Wr/S]×Cpm(m) (9) 若消费者产品使用率分布的密度函数为g(r),则所有消费者在整个质保期内的期望成本为: (10) 在汽车质保服务中,基于预防性维修的质保策略优化是以总成本最小化为目标的规划问题: minECT(S,m) s.t.0 0≤m≤M 为了检验基于里程的预防性维修策略优化对于降低产品质保期维修成本的具体效果,笔者对3类不同汽车质保期组合中的预防性维修策略进行了优化研究,分别是(3,3),(3,6),(6,6),其中(3,3)代表质保时间为3年,质保里程为3万km。分析了不同质保期组合下采用该预防性维修策略对质保成本的影响,并对关键参数的敏感度进行了有效分析。汽车故障率中相关参数为θ0=0.1,θ1=0.2,θ3=0.7,θ4=0.7。汽车产品使用率在[0.5,3.5]内服从均匀分布,有g(r)=1/(rmax-rmin)。预防性维修的维修程度m=0,1,…,5,对应的预防性维修成本分别为Cpm=(0,10,30,60,100,160),平均最小维修费用Cmin=250元。 笔者对3种不同汽车质保期组合下基于固定里程的预防性维修策略进行了优化研究,并计算了不同预防性维修程度下使汽车质保期内成本达到最小化的最优固定里程,以及相应的修正性维修成本和预防性维修成本,如表1所示。研究结果表明,预防性维修的实施能够有效降低修正性维修的期望成本,在不同质保期组合下实施预防性维修策略都能够有效降低汽车质保期内的期望成本。当保证期组合越长时,实施预防性维修对成本降低起到的作用越明显,如质保期组合为(6,6)时,实施基于里程的预防性维修策略能够使得质保服务成本最高降低41.18%。 表1 预防性维修策略模型的优化分析 注:ECT为实施固定里程预防维修的期望质保成本;ECC为未实施预防维修的期望质保成本;R为实施预防性维修策略后期望质保成本的降低比率 为了进一步说明该预防性维修策略的有效性,笔者还对比了采用固定使用里程和固定时间间隔预防性维修策略时汽车质保期内整体期望成本的大小。在3种不同汽车质保期组合下,分别对采用固定里程的预防性维修策略和定期预防性维修策略进行了优化研究,如表2所示。 表2 定期预防性维修与基于固定里程预防性维修优化结果对比分析 注:T为维修时间间隔;ECR为实施定期预防性维修的期望质保成本 研究结果表明,两种不同的预防性维修策略在不同情境下各有优劣,部分情况下采用定期预防性维修能够使质保服务成本最小化,而部分情况下采用基于固定里程的预防性维修策略能够使质保成本最小化。两种方案各自有不同的适用环境,与产品故障率函数、消费者产品使用率分布等密切相关。因此,构建基于使用里程的预防性维修策略,可以作为基于时间定期预防性维修策略的有效补充,其设计和优化研究具有非常重要的理论意义与实践价值。 以汽车质保期为例,笔者对最小维修成本期望值在不同取值情况下的预防性维修策略进行了优化研究,获得了使质保成本最小化的最优预防性维修程度与固定使用里程。研究结果如表3所示,结果表明单位修正性维修与单位预防性维修成本之比对于维修策略具有重要影响。如随着单位最小维修成本的逐渐增高,所需预防性维修的程度越来越高,预防性维修的固定里程间隔则越来越短,意味着当修正性维修费用较高时,需要更多、更高程度的预防性维修服务来降低整体质保服务成本。一般情况下,当修正性成本相对于预防性维修成本较大时,采取预防性维修服务对于整体成本降低就越为明显。当修正性维修成本相对较高时,减小预防性维修的固定使用里程间隔,提高预防性维修次数能够有效降低质保成本;相反,当修正性维修的期望成本相对较小时,可以通过增加预防性维修的固定使用里程间隔来减少预防性维修次数,从而使得质保成本最小化。 表3 预防性维修敏感度分析 注:CM为质保内最小维修成本;CP为质保内预防维修成本 通过总结与对比国内外关于汽车质保维修策略的最新研究成果,在已有研究基础上提出了基于固定使用里程的预防性维修策略,将其有效应用到了汽车二维质保服务中并进行了优化研究。结果表明,该维修策略作为基于固定时间的定期预防性维修策略的有效补充,同样可以有效地降低汽车质保期内的整体维修成本,其在理论和实践应用中都具有重要意义。当前研究还可以在以下几个方面进行补充与完善。 (1)当前研究中最小维修和预防性维修在汽车质保期不同阶段的期望成本是固定不变的,而在实际中相应维修成本可能会随着产品使用时间或使用里程的不断增长而增长。因此,分析和拟合质保期内不同阶段的修正性维修成本和预防性维修成本,设计基于变动维修成本的质保期内维修策略优化值得进一步研究。 (2)针对当前多采用定期预防性维修策略的研究现状,笔者构建了基于固定使用里程的预防性维修策略,并将其有效应用到了汽车质保维修中。如何在预防性维修策略中同时考虑使用时间和使用里程,设计基于时间、里程的二维预防性维修策略同样值得进一步深入研究。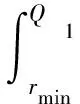
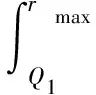
2 算例分析
2.1 预防性维修策略的优化分析
2.2 参数敏感度分析
3 结论
