基于结构优化技术的顶盖结构设计方法研究
2018-09-06罗慧娟苏晓宇付广
罗慧娟,苏晓宇,付广
(上汽通用五菱汽车股份有限公司技术中心,广西柳州 545007)
0 引言
汽车顶盖主要由顶盖外板和顶盖横梁组成。顶盖由于外板刚度较低,且具有较大的声辐射面积,其固有频率容易与车内空腔和发动机的二阶振动耦合,激发车内噪声。此外,顶盖外板在日常使用过程中常会受到外载荷的作用,如人为的触摸按压、积雪的静载荷及碎石冲击等,使顶盖发生外板凹陷及结构失稳等现象。因此,在设计时,需要兼顾模态、抗雪压性及抗凹性的要求。
目前,对于单一性能的影响因素及性能提升方法研究已较深入,但各因素对模态、抗雪压及抗凹性的影响却存在相互制约的现象。例如:顶盖外板加筋条在提升抗雪压性及抗凹性的同时,却降低了模态。在轻量化设计成为必然的大环境下,顶盖的覆盖件及横梁已越来越薄。如何在兼顾轻量化同时,设计出满足顶盖模态、抗雪压及抗凹性的顶盖结构,成为困扰设计人员的问题。
结构优化技术是当前CAE(Computer Aided Engineering)技术发展的一个热点,通过优化技术可以在质量最小的前提下,使结构的性能达到最优。目前,在工业界的应用已逐渐成熟。文中主要探讨在顶盖结构的设计过程中,如何利用结构优化技术,在兼顾轻量化设计的前提下,使顶盖各性能满足设计要求。
1 结构优化技术
优化设计有三要素,即设计变量、目标函数和约束条件。设计变量是发生改变从而提高性能的一组参数;目标函数要求最优的设计性能,是关于设计变量的函数;约束条件是对设计的限制,是对设计变量和其他性能的要求。优化数学模型可表述为:
Minimize:f(X)=f(x1,x2,……,xn)
Subject to:g(X)≤0j=1,……,m
hk(X)≤0k=1,……,mh
其中:X=(x1,x2,……,xn)是设计变量,如产品的结构尺寸等;f(X)是设计目标,如各种力学性能或者质量;g(X)和h(X)是需要进行约束的设计响应,如对产品工作时的变形和应力水平进行约束。
1.1 基于OptiStruct的优化方法
OptiStruct是一个面向产品设计、分析和优化的有限元和结构优化求解器,它提供拓扑优化、形貌优化、尺寸优化、形状优化及自由尺寸和自由形状优化,这些方法被广泛应用于产品开发过程的各个阶段。此研究涉及其中3种优化设计方法:形状优化、形貌优化与尺寸优化。
在形貌优化中,设计空间由大量的节点波动向量组成,这些节点波动向量按照一定的模式进行组合以满足设计约束,并最终生成优化后的最佳形貌。此优化方法适用于在钣金件上找出最佳的加强筋位置和形状。在形状优化中,通过将网格节点移动到新的位置,改变零件的形状,从而提高零部件的性能。此种优化方法常用于优化零件的位移和几何形状。OptiStruct形状优化采用非参数化的优化方法,将设计空间分成若干控制区域, 每个区域的形状简化为关键控制节点位置, 通过移动这些关键节点, 产生边界形状的变化。形状设计变量为关键节点的位置。在尺寸优化中,网格模型保持不变,只改变模型的参数,可以对有限元模型的各种参数,如板件厚度、材料特性等进行优化。
1.2 汽车顶盖结构优化设计技术路线
以结构优化结果为指导,进行顶盖结构设计。首先,对影响顶盖各性能的因素进行分析,并将其转变为可参数化的设计变量;其次,进行顶盖结构初步设计,并针对不同的设计变量选择适合的优化方法;最后,依据优化后的设计变量进行顶盖的详细结构设计,并校核其性能是否满足设计要求。
影响顶盖性能的因素可分为两类:一类为顶盖外板,另一类为顶盖横梁。顶盖外板因素一般包括顶盖外板曲率分布、有无筋条、筋条数量、筋条形状等,顶盖横梁变量一般包括横梁数量、横梁位置、横梁的形状及厚度。顶盖外板为双曲率大平面,曲率是不易优化的变量,为此,将顶盖曲率转变为顶盖弦高进行处理。
优化外板变量不需要增加质量,且对各性能的影响较大,因此先优化外板变量,再优化横梁变量。由于外板变量对各性能的影响规律不一,按先确定顶盖外板曲率分布、再确定筋条数量、最后确定筋条形状的设计思路,进行外板变量的优化。以需要对顶盖全部的影响因素进行优化为例,顶盖结构的优化设计路线如图1所示。
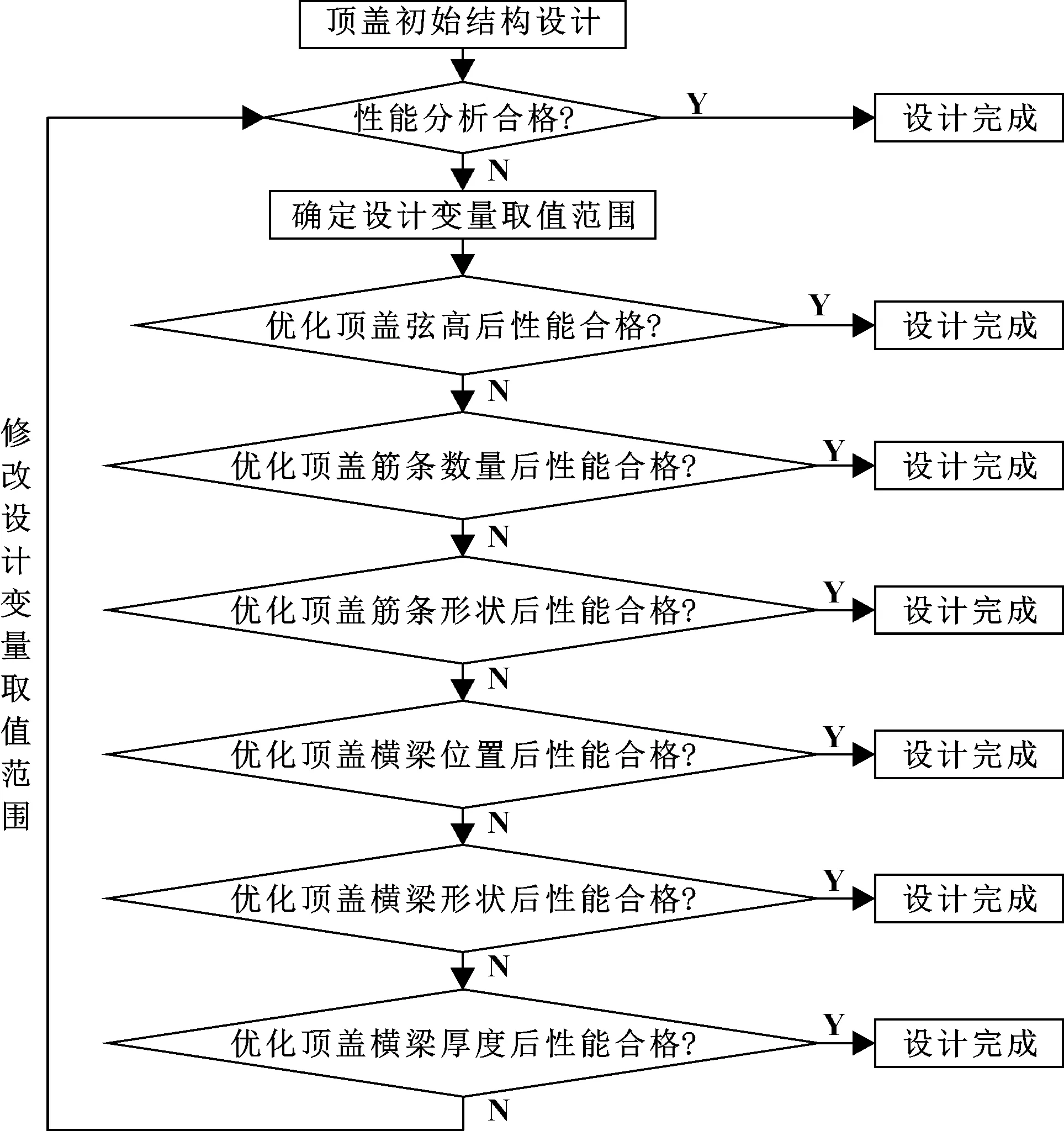
图1 顶盖结构优化设计技术路线
2 顶盖初始结构设计
文中以某车型顶盖结构为例,进行结构优化设计。首先进行顶盖初始结构设计,并分析其各项性能。
2.1 初始结构设计方案
顶盖初始结构设计在满足总布置要求及侧碰等关键约束要求的基础上进行,主要遵循以下几条原则:(1)根据造型A面设计顶盖外板;(2)根据侧碰性能要求及顶盖安装等总布置要求确定横梁的数量及布置;(3)在满足前两项要求的前提下,按照质量最轻的轻量化原则进行顶盖结构设计。
顶盖结构的初始设计方案如图2所示,顶盖总成各零件的初始设计厚度如表1所示。
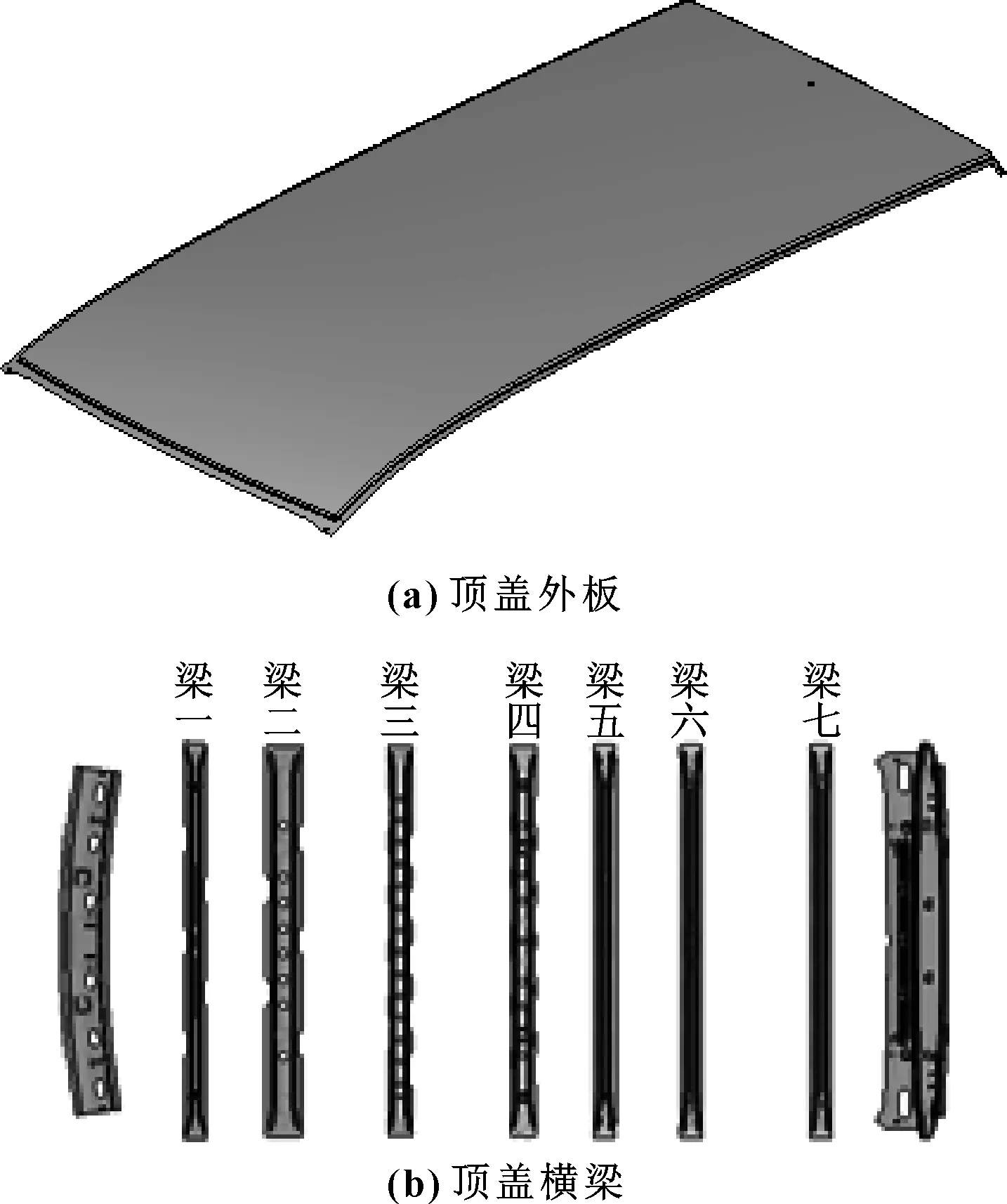
图2 顶盖初始结构设计方案
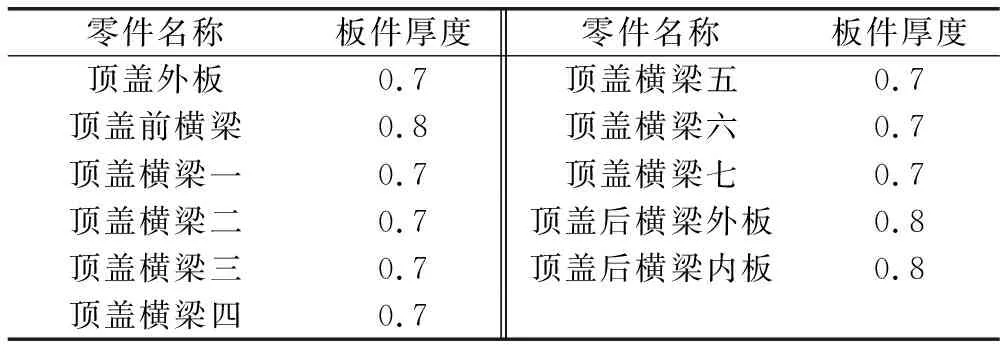
表1 顶盖零件设计厚度mm
2.2 初始结构性能分析
对初始设计方案的各性能进行有限元分析。为模拟顶盖的边界条件,分析模型截取一部分的白车身结构,并在阶段处约束全部自由度,顶盖结构性能分析有限元模型如图3所示,各性能指标及分析方法如表2所示。
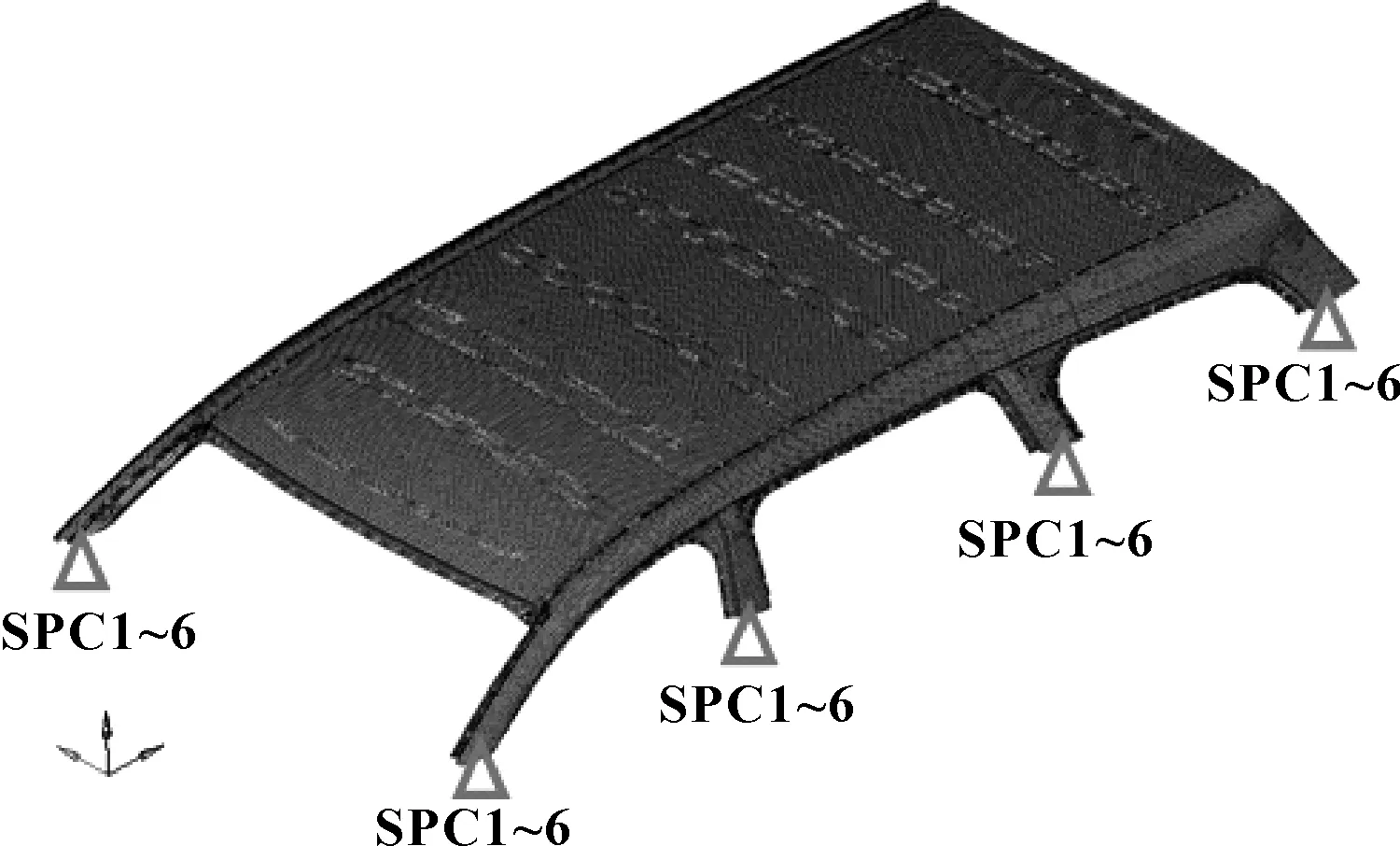
图3 顶盖结构性能分析模型

分析项初始设计结构分析值目标值分析方法质量/kg22.4323———模态/Hz47.8945模态分析,一阶模态抗凹初始刚度/(N·mm-1)17(最弱处)>20非线性分析,初始刚度抗雪压/cm33>70屈曲分析,一阶屈曲因子
从初始结构的性能分析结果来看,除了模态结果达标外,其他的性能均不达标,需要进行优化设计。
3 顶盖结构优化设计
根据总布置、造型及质量等要求,在初始结构的基础上,可优化的设计变量为顶盖弦高、加4~6根筋条、筋条形状,及优化横梁五、横梁六、横梁七的截面尺寸。设计变量的取值范围及优化方法如表3所示。

表3 某车型顶盖设计变量、取值范围及优化方法
3.1 顶盖弦高优化
选择顶盖外板的弦高作为形状设计变量,使用HyperMorph创建包含顶盖外板和横梁的控制块,合理划分控制块,将模型分成多个域。通过移动控制块的控制柄使顶盖的弦高发生变化。设置优化问题描述如下:(1)设计变量为顶盖最高点处的控制柄位置,取值范围:Z正向移动0~17 mm;(2)设计约束为一阶模态频率大于45 Hz;(3)设计目标为一阶屈曲因子最大。
运行OptiStruct 软件对顶盖的弦高进行优化计算,优化结果如图4(a) 所示,当设计变量取最大值时,一阶模态大于45 Hz,一阶屈曲因子最大。根据优化结果,将顶盖弦高提高17 mm,优化后的顶盖外板如图4(b)所示。对优化后结构进行性能校核,一阶模态61.02 Hz;一阶屈曲因子0.86(对应抗雪压厚度60 cm);抗凹性能最弱点初始刚度17.5 N/mm。
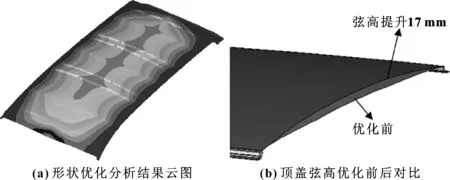
图4 顶盖弦高优化——形状优化
顶盖弦高优化后,模态满足要求,抗雪压厚度由33 cm提升至60 cm,抗凹初始刚度提升不大。抗雪压性与抗凹性仍不满足目标值的要求,需进一步优化。
3.2 筋条数量优化
设置顶盖横梁二与顶盖后横梁间的顶盖外板区域为优化区域,优化区域X向长度1 680 mm。起筋的参数定义:起筋的最小宽度67 mm,起筋角度60°,起筋高度5 mm。沿X向设置线性起筋约束,设置优化问题描述如下:(1)设计变量为优化区域内节点相对壳单元中性面法向的扰动;(2)设计约束为一阶模态频率大于42 Hz,一阶屈曲因子大于1;(3)设计目标为在顶盖大面上施加均布力对应的工况柔度最小。
运行OptiStruct 软件对后地板加强筋布局进行优化计算,顶盖外板起筋形式如图5(a)所示。根据分析结果,在顶盖外板上起4根长1 680 mm、宽77 mm、高5 mm的筋条,结构如图5(b)所示。对优化后结构进行性能校核:一阶模态42 Hz,一阶屈曲因子1.2(对应抗雪压厚度84 cm),抗凹初始刚度21.5 N/mm。
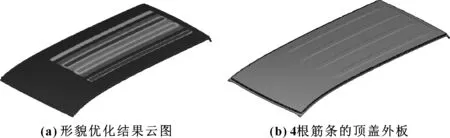
图5 筋条数量优化——形貌优化
增加筋条后,虽然抗雪压性能与抗凹性能满足要求,但模态由61.02 Hz下降至42 Hz,需进一步优化筋条的形状。
3.3 筋条形状优化
根据造型区域设计,选择筋条长度作为形状设计变量,使用HyperMorph在筋条末端(即靠近车尾端)创建域和控制柄。通过移动控制柄使筋条的长度发生变化。设置优化问题描述如下:(1)设计变量为筋条末端的控制柄位置,取值范围:X正向移动0~300 mm;(2)设计约束为一阶屈曲因子大于0.9;(3)设计目标为模态最大。
运行OptiStruct 软件对筋条的长度进行优化计算,优化结果如图6(a) 所示,筋条长度缩短290 mm。结合造型区域的要求,优化后的筋条如图6(b)所示。对优化后结构进行性能校核:一阶模态45.3 Hz,一阶屈曲因子0.9(对应抗雪压厚度63 cm),抗凹初始刚度20.4 N/mm。
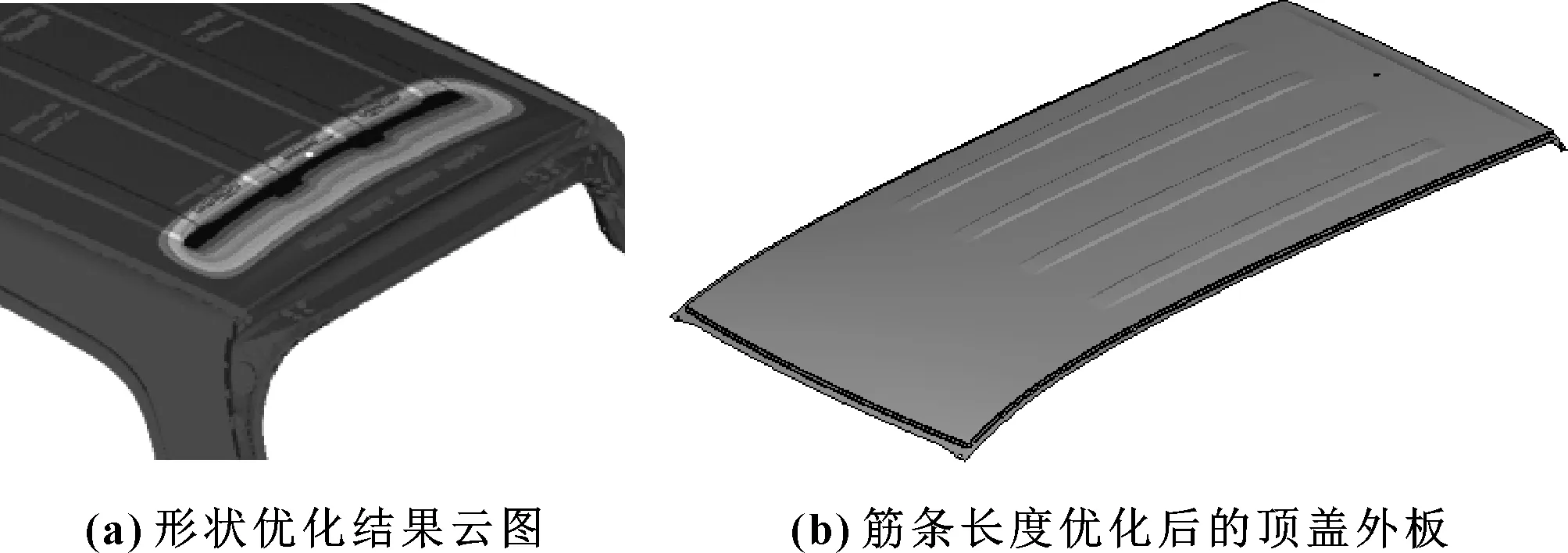
图6 筋条形状优化
筋条的长度从尾端起缩短290 mm后,模态提升的同时,抗雪压性能下降,抗凹初始刚度变化不大。从分析结果看,模态与抗雪压性能虽然都不满足设计目标,但离目标值很近,需进一步优化顶盖横梁的设计变量。
3.4 横梁形状优化
选择横梁五、横梁六、横梁七的宽和高作为形状设计变量,使用HyperMorph创建横梁宽度尺寸和高度尺寸的域和控制柄。通过移动控制柄使横梁的截面形状发生变化。设置优化问题描述如下:(1)设计变量为横梁截面的控制柄位置,取值范围:X正负向移动0~15 mm;Z负向移动0~5 mm;(2)设计约束为一阶模态大于45 Hz、一阶屈曲因子大于1;(3)设计目标为质量最小。
运行OptiStruct 软件对横梁的截面形状进行优化计算,优化结果如图7(a) 所示,当横梁的Z向尺寸沿负Z向增加10 mm,横梁五、六、七的X向尺寸以梁中心位置扩宽5 mm,一阶模态大于45 Hz,一阶屈曲因子大于1。根据优化结果,以宽27 mm、高27 mm设计横梁五、六、七截面,优化后的截面尺寸如图7(b)所示。对优化后结构进行性能校核:一阶模态46.2 Hz;一阶屈曲因子1.3(对应抗雪压厚度91 cm);抗凹初始刚度20.4 N/mm。由于截面变大,质量增加0.35 kg。
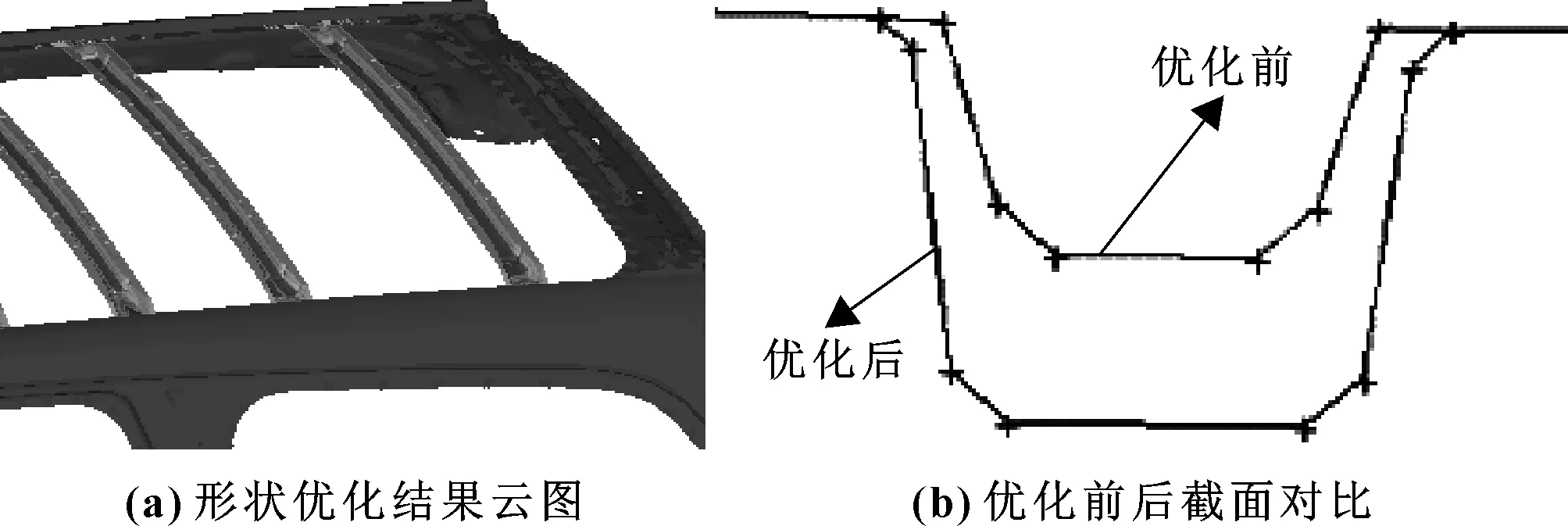
图7 横梁形状优化
横梁截面形状优化后,顶盖的各项性能均满足设计目标要求,不需要再进行优化。
3.5 顶盖结构优化设计
经过以上结构优化,顶盖的各项性能指标已满足设计目标要求。根据优化过程中各设计变量的最优值进行顶盖结构设计,最终的顶盖结构如图8所示。

图8 顶盖优化设计结构
由优化过程可知:在顶盖初始结构的基础上,经过优化设计,仅增重0.355 kg,即使顶盖各项性能满足设计目标要求。增重后,顶盖质量为22.785 kg,比目标值低,满足轻量化的设计要求。
4 结论
(1)基于结构优化技术的顶盖设计方法,在满足总布置要求及侧碰等关键约束要求的基础上,以质量最轻为原则进行顶盖初始结构设计,在优化过程中优先优化不增重的设计变量,保证了顶盖结构的轻量化设计;
(2)在运用结构优化技术对设计变量进行优化的过程中,通过合理选择优化方法、设置优化目标和约束,在变量的取值范围内找到最优化值,为设计出满足顶盖模态、抗雪压及抗凹性的顶盖结构提供了指导,避免了设计反复。
