不同诱导结构对折叠式压溃管动态吸能影响

梁玉，姚松，许平，周志鹏

不同诱导结构对折叠式压溃管动态吸能影响

梁玉，姚松，许平，周志鹏

(中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙 410075)

建立带预压结构的折叠式压溃管有限元模型，得到其动态冲击下轴对称变形模式和撞击力−位移曲线，对折叠压溃管进行动态冲击实验，有限元仿真结果与实验结果的变形模式和撞击力−位移曲线吻合良好，验证了有限元模型的准确性。通过仿真分析发现预压缩能减小圆管在动态冲击下的第1个褶皱波长，但对整体变形模式和撞击平台力大小基本无影响。在此基础上，对无预压圆管开设4种不同的诱导结构：外表面开槽诱导和内外表面交替开槽诱导、外波纹诱导、内外表面波纹管诱导，分析发现内外表面交替开槽和内外波纹管诱导结构能控制圆管的变形模式，外表面开槽诱导对圆管的褶皱波瓣形状有一定影响，外表面波纹诱导会让圆管呈现一定的非对称变形。与初始圆管相比，4种诱导圆管中，只有外部开槽诱导下的圆管比吸能增大，同时载荷波动系数减小29.4%，撞击平台力与初始圆管基本相当。本文可为折叠式压溃管吸能特性优化提供参考。

折叠式压溃管；预压缩；诱导结构；载荷波动系数

折叠式压溃管以其经济、轻质和高效的优点被广泛应用于高速列车、汽车等被动吸能装置。从Alexander[1]率先提出轴向压缩下圆管的圆环变形假设模型，Wierzbicki等[2]建立考虑褶皱弧度的圆管变形模型，以及Singace等[3]考虑偏心率的圆管轴对称变形模型以来，越来越多的学者通过理论、实验和数值分析的方法对薄壁圆管的动态吸能特性进行了探究和改进。关于薄壁圆管结构本身诱导结构的改进，Daneshi等[4−6]通过实验探究了轴向准静态压缩下，圆管薄壁结构内外表面开设交替刻槽可以控制其变形顺序，开槽距离对撞击峰值力、平台力和吸能量有一定影响，同时对撞击峰值力和平台力进行了理论分析和预测。WEI等[7]研究了在薄壁圆管内外表面开设变厚度刻槽，通过理论分析、落锤实验和数值仿真得出了影响结构变形和吸能特性的3个重要的无量纲参数。YANG等[8]通过激光熔化金属3D打印技术制造出管壁内部有刻槽的薄壁结构，并通过实验和数值仿真发现这种新型结构同时具有屈曲和撕裂两种变形模式，为工程应用提供了一种新型结构。与在薄壁结构表面或内部开设刻槽的诱导结构相对应，Salehghaffari等[9]研究了在结构外部增设增厚环的薄壁圆管，发现增厚环的尺寸和位置对准静态下结构的比吸能和峰值力有很大影响，并通过响应面法对增厚坏参数进行了单目标和多目标优化得到比吸能最大化峰值力最小化的增厚环结构。SUN等[10]研究了轴向变厚度的阶梯管，发现变厚度梯度指数对阶梯管的比吸能和峰值力有很大影响。Rajabiehfard等[11]用冲击实验和数值仿真对比了均匀管、变厚度阶梯管和圆锥管的吸能特性，发现变厚度阶梯管的动态吸能特性与圆锥管类似。近年来，另外一种薄壁诱导结构的波纹管引起了国内外大多学者的广泛兴趣。CHEN等[12]研究了轴向压缩下，波纹管相对于普通圆管而言变形模式更加可控，压缩力−位移曲线的振荡更小，波纹波长和幅值对波纹管的变形模式和吸能特性有显著影响。Eyvazian等[13]通过准静态压缩实验探究了轴向外表面波纹诱导薄壁铝管的变形模式和吸能特性。LIU等[14]通过理论和数值仿真探究了波纹管的变形机理，得到冲击速度和径厚比对变形模式和吸能特性的影响。WU等[15]探究了波纹管的波长、幅值、径厚比对其初始峰值力、载荷曲线、吸能特性的影响，并用响应面方法优化了波纹管结构。本文研究的折叠式压溃管亦属于薄壁圆管，通过以上分析发现以往的研究基本上都是在准静态工况下，研究诱导结构对薄壁圆管性能的影响，在动态冲击载荷下，不同诱导结构对薄壁圆管的影响还需进行深入的研究。基于此，本文通过基于LS- DYNA的数值仿真和动态冲击实验研究折叠式压溃管的吸能特性，并在其基础上开设4种不同的诱导结构：外表面开槽诱导、内外表面交替开槽诱导、外波纹诱导、内外表面波纹管诱导，分析在动态冲击条件下，不同诱导结构对折叠式压溃管的变形模式和吸能特性的影响。

1 折叠式压溃管有限元仿真

1.1 有限元模型的建立

为了研究折叠式压溃管动态冲击下的吸能性能，参照现有机车折叠式压溃管的结构和尺寸建立有限元碰撞仿真模型，如图1所示，由折叠式压溃管组成的吸能结构主要由4部分构成：2内衬(连接上下部分，起定位作用)，底板(处于底部，起支撑作用)，以及吸能圆管(中间带梯度厚度和过渡圆弧，主要起吸能作用)。圆管中间变形部分的内外直径分别为60 mm和70 mm，下部阶梯加厚部分的外径为73 mm，内径同变形部分内径尺寸相同为60 mm。在进行碰撞之前对试件进行12 mm的准静态压缩，带预压缩量的试件总长为180 mm。

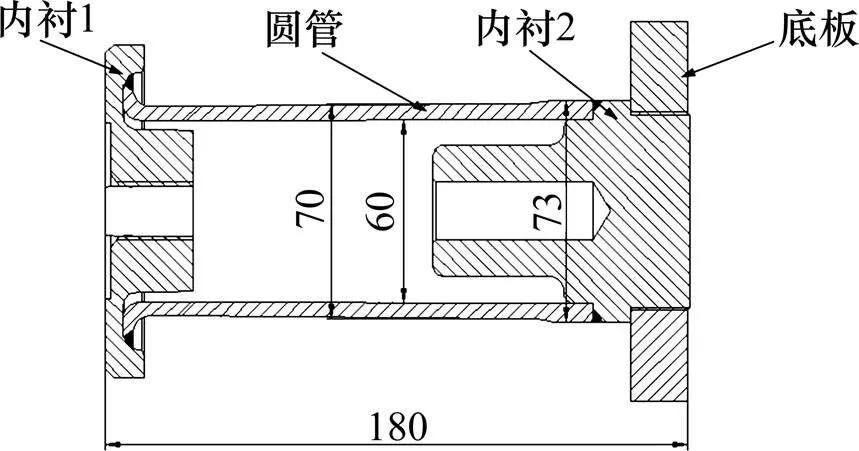
图1 折叠式压溃管结构示意图

基于Hypermesh建立折叠压溃管的有限元模型，如图2所示，忽略对变形影响不大的非撞击端内衬结构和底板，右端设为刚性墙，左端具有一定质量的钢板用来给定初始动能。为了保证计算精度，进行网格敏感度分析，结果表明，1 mm的单元尺寸收敛性比较好，且整个模型采用全积分算法实体单元。

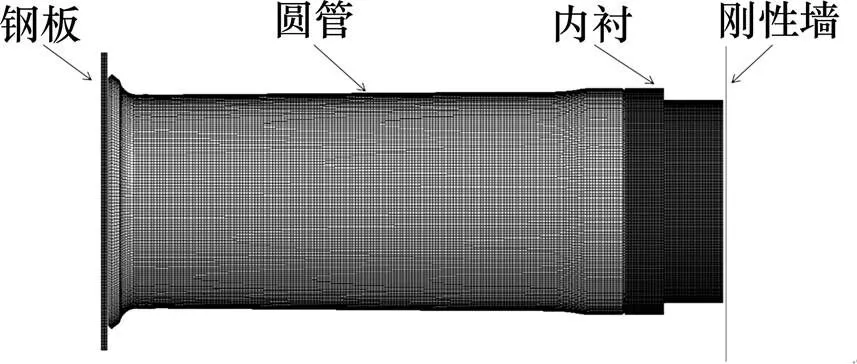
图2 简化有限元模型

用自动单面接触算法来模拟圆管自身由于屈曲变形而产生的接触，动、静摩擦因数分别设为0.025和0.03，钢板和内衬都视为刚性体，用刚体与弹性体之间的连接*constrained_extra_node_set接触分别来模拟吸能圆管与内衬、吸能圆管与钢板的接触。

吸能结构的吸能圆管材料为高级低合金钢，其材料的有效应力−应变曲线见图3，在LS-DYNA中用24号材料*MAT_PIECEWISE_LINEAR_PLAS- TIC来模拟，忽略应变率影响。内衬和钢板视为刚性体，用20号材料*MAT_RIGID来模拟。材料具体参数见表1。

根据文献[16]建立折叠式压溃管的准静态预压缩模型，由于准静态数值模拟所用的时间很长，如果吸能结构在变形过程中的动能占内能百分比小于5%，可用显式数值计算代替准静态压缩的隐式计算来提高计算效率。为了实现吸能圆管结构的预压缩，如图4(a)所示，约束钢板的自由度，给刚性墙输入一定初始能量对圆管进行动态预压缩12 mm，添加控制卡片*INTERFACE_ SPRINGBACK_ LSDYAN_ NOTHICKNESS，生成一个dynain文件，此文件储存了模型最后时间步的应力应变及网格数据。动态预压缩过程中圆管的动能与内能变化趋势见图4(b)所示，圆管的最大内能为4 996.1 J，最大动能为2.742 J，动能与内能的比值为0.5%，小于5%，可以将此动态预压缩过程视为对圆管的准静态压缩模拟。

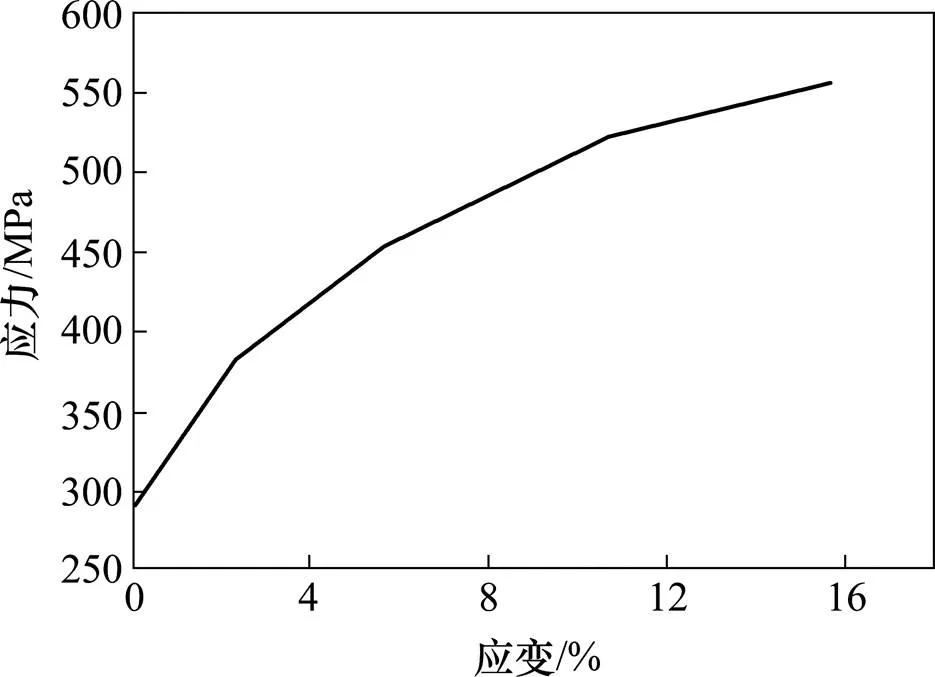
图3 吸能圆管有效应力-应变曲线

表1 具体材料参数

1.2 有限元结果分析

根据实验台车的总质量，为保证有限元模型与之后的实验验证条件尽量一致，将钢板的质量与台车的质量一致设为12.65 t，给定模型初速度为2.7 m/s进行动态冲击仿真，得到数值真变形结果及撞击力位移曲线如图5所示。

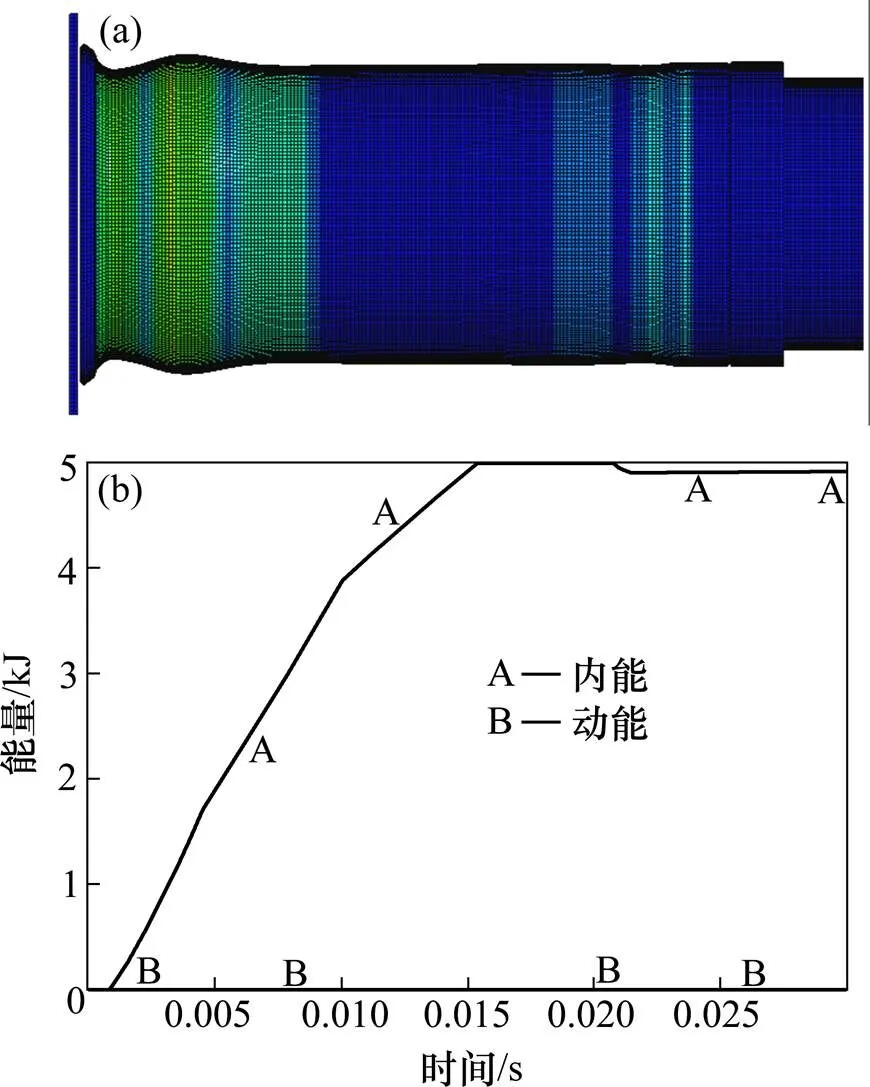
图4 预压缩模型和圆管动能与内能变化趋势

(a) 变形结果；(b) 撞击力位移曲线

由图5可知，折叠式压溃管共形成了3个吸能褶皱，与撞击力−位移曲线的3个波峰波谷一一对应。在初始峰值力出现之后，整体撞击力在300~600 kN之间波动，在冲击速度为2.7 m/s时，压溃管 的有效撞击行程和有效吸能量为分别为93 mm 和47 kJ。

折叠式压溃管的变形模式为轴对称模式，但是撞击力波动比较剧烈。为了能更加优化折叠式压溃管的吸能特性，本文展开诱导结构对折叠式压溃管的吸能特性研究。在此之前，先进行折叠式压溃管的动态冲击实验以验证有限元模型的准确性。

2 折叠式压溃管实验验证

冲击实验在中南大学轨道交通安全教育部重点实验室的碰撞实验台上进行。实验用到的测试系统主要包括速度触发系统、12.65 t台车、测力刚性墙、撞击力采集系统、速度测试系统和高速摄影系统。实验现场的总体布置如图6所示。

图6 折叠式压溃管冲击实验总体布置

将折叠压溃管固定在冲击台车前端，台车及试件的总质量约为12.65 t。台车通过空气炮得到触发速度=2.7 m/s，速度测试系统可以记录台车及试件撞击刚性墙时的瞬时速度，试件与刚性墙的撞击力由固定在刚性墙上的4个力传感器采集，传感器的采样频率为20 k，同时高速摄影系统以10 k的频率捕捉试件的变形形态以及压缩过程。

将同等速度下的有限元模型结果与实验结果进行对比，分析两者之间变形模式、撞击力和能量吸收的差异，验证折叠式压溃管有限元模型的准确性。有限元仿真与实验结果的变形模式和撞击力−位移对比见图7。

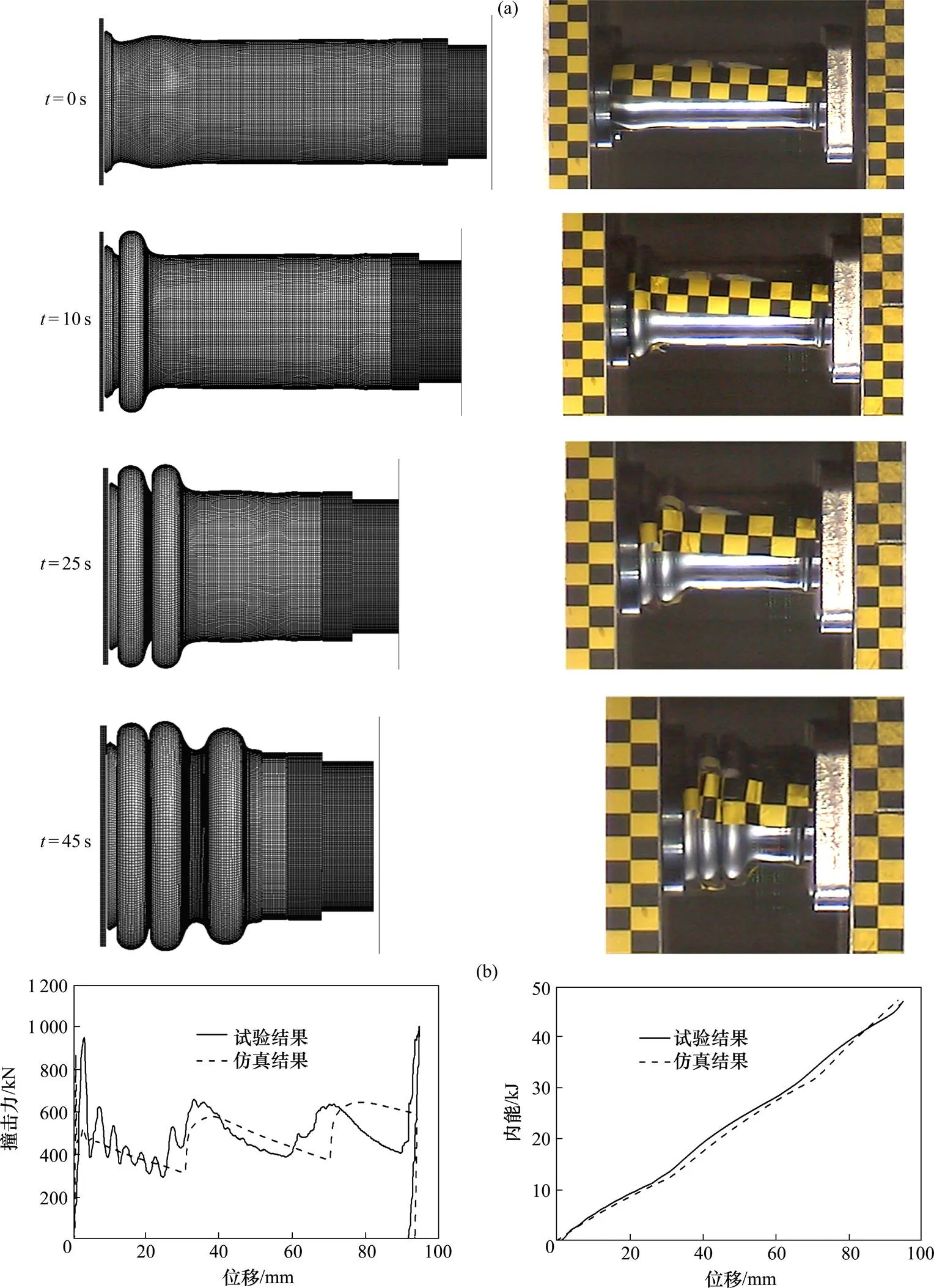
(a) 变形模式；(b) 撞击力−位移和内能趋势曲线

由图7(a)可知，有限元仿真结果的变形模式和实验结果基本一致，产生的褶皱数目相同，由图7(b)可知，有限元仿真撞击力−位移曲线变化趋势与实验结果基本相同，内能变化趋势一致，吸能量相近。最后实验结果的撞击力−位移曲线出现骤升现象是由于吸能圆管完全压实后2内衬相互接触，由于2内衬刚度较大，导致撞击力骤升。而仿真模型省略了非撞击端内衬，因此吸能圆管压实后没有产生刚体与刚体之间相互碰撞的撞击力。通过图7变形模式和撞击力−位移以及内能变化趋势曲线对比验证了本文有限元模型的准确性。

3 不同诱导结构对折叠式压溃管吸能特性的影响

3.1 预压缩对折叠式压溃管的影响

为了探究吸能圆管在动态冲击前的预压对变形模式和吸能性能的影响，在LS-DYNA中将无预压缩的模型进行动态冲击模拟，无预压缩和有预压缩结构变形模式和撞击力−位移曲线对比结果见 图8。

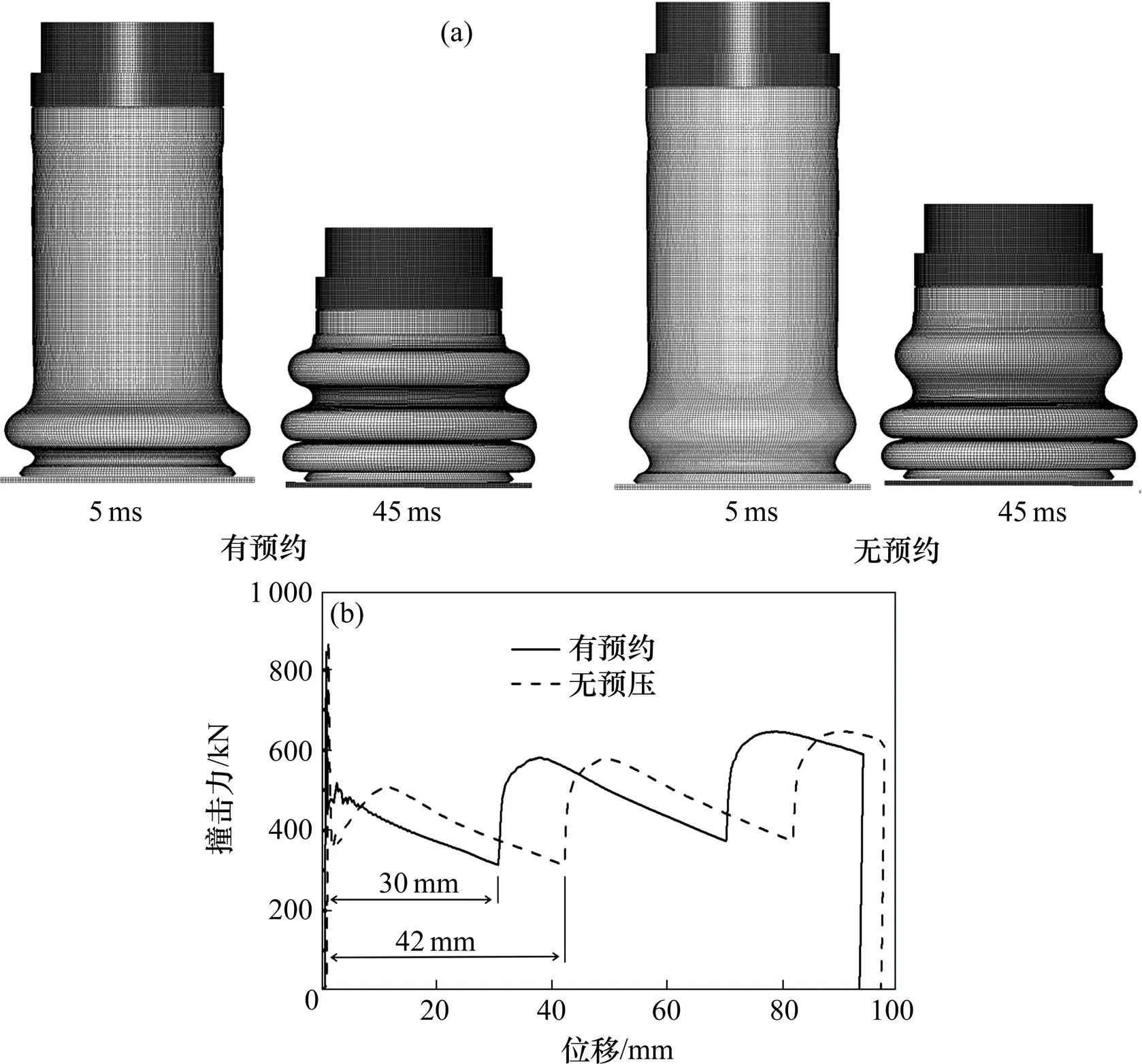
(a) 变形模式；(b) 撞击力−位移曲线

从图8(a)和8(b)可以看出，在5 ms时刻，有预压结构的圆管基本完成了第1个褶皱的形成，但是无预压结构的圆管第1个褶皱才形成一半，所以预压能够让圆管的第1个褶皱更早形成，在45 ms时刻，2圆管都完成折叠压缩，变形模式基本相同，但由于预压缩的存在，吸能结构的压缩量变大。从图8(c)可以看出，有预压结构的第1个褶皱波峰波谷距离为30 mm，无预压结构的第1个褶皱波峰波谷距离为42 mm，但两者平台力相差不大。所以预压缩能减小吸能结构第1个褶皱的波长，但对结构的总体吸能和变形模式无影响。为了缩短计算时间，后文探究圆管表面诱导结构对结构变形模式和吸能特性的影响应用无预压的有限元模型来进行有限元仿真。

3.2 圆管表面诱导结构对折叠式压溃管的影响

为了探究圆管表面不同诱导结构对折叠式压溃管变形模式和吸能特性的影响，对吸能结构圆管表面开设4种不同诱导结构。如图9所示，方式1是在圆管外表面等距离开设1 mm深的矩形槽，槽宽6 mm，槽间距为20 mm，槽数量为6个。方式2是在圆管内外表面等距间隔开设1 mm深的矩形槽，槽的尺寸、位置和间距同方式1保持一致。方式3是在圆管外部开设正弦波纹形状，波纹数为6个，正弦波的波长为20 mm，幅值为1.5 mm。方式4为圆周内外都为正弦波纹的波纹管，波纹数为6个，和方式3一样，正弦波波长为20 mm，幅值为1.5 mm。以上4种模型平均直径和原圆管一样为68 mm，刚性墙压以10 m/s的恒定速度压缩圆管90 mm，以探究4种诱导结构下圆管的变形模式和吸能特性。

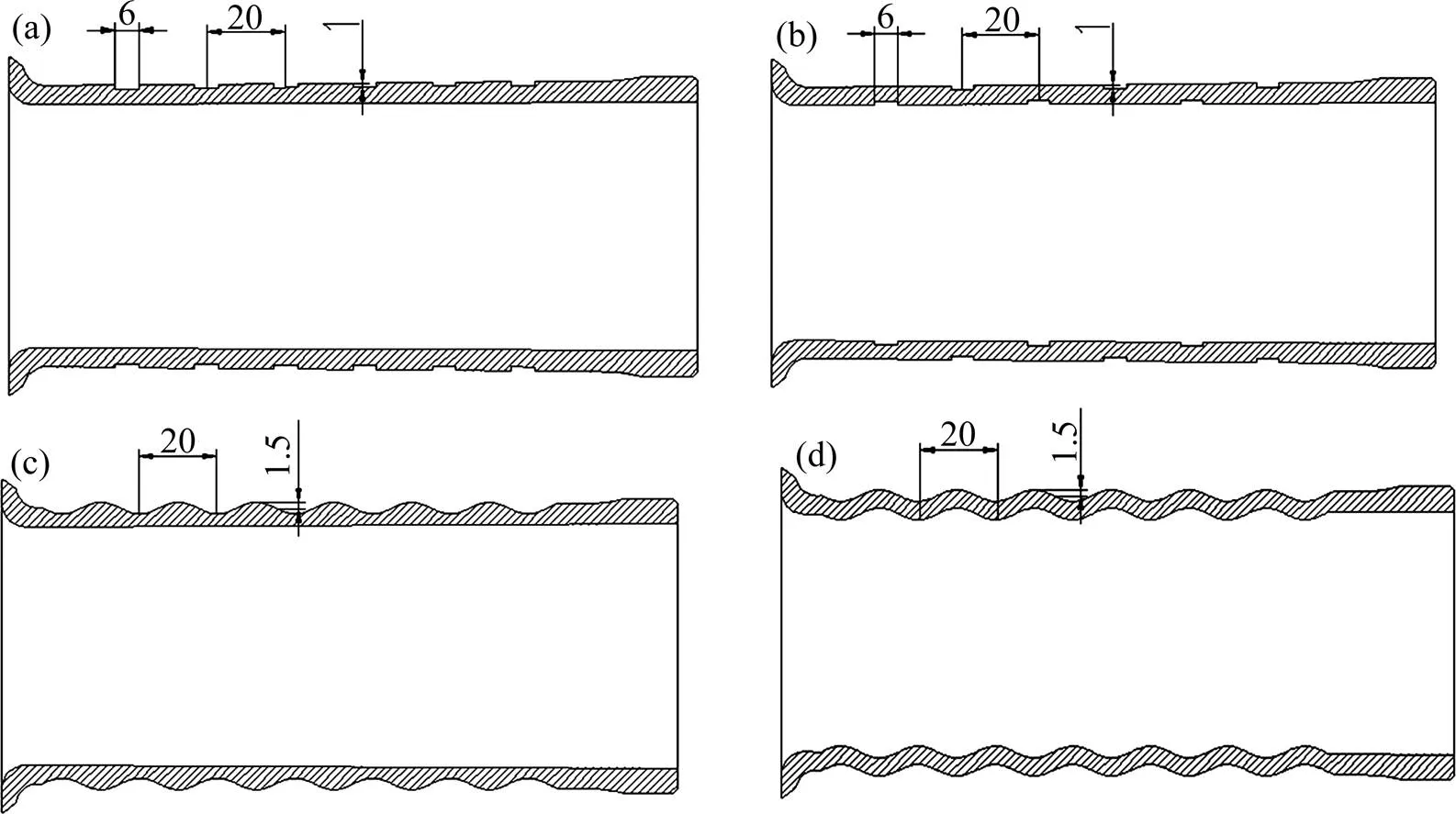
(a) 方式1；(b) 方式2；(c) 方式3；(d) 方式4

3.2.1 诱导结构对变形模式的影响

每种诱导结构均对圆管的变形模式产生了一定的影响。图10为初始圆管和4种诱导结构下圆管动态冲击下的变形过程，图11为对应的不同诱导结构圆管的撞击力−位移曲线。

由于有内衬的存在，撞击开始的峰值力是内衬与刚性墙的接触力，所以由图11可知，原圆管和4种诱导结构下的圆管的峰值力基本没变。由图10(a)和11(a)可知，初始圆管共形成了2个半褶皱，每个褶皱对应地产生了波峰与波谷，波峰波谷浮动比较大，但整个过程撞击力都稳定在300~600 kN。由图10(b)和图11(b)可知，方式1的外部开槽对圆管内外褶皱波瓣的形状形成有一定影响，方式1的诱导结构第1个褶皱形成的位置和撞击力曲线和初始圆管相似，之后的变形由于圆周外部开槽的存在，影响了第2和第3个褶皱波瓣的形状，从而影响撞击力曲线，撞击力曲线波动比初始圆管更小。由图10(c)和图11(c)可知，方式2的诱导完全改变了圆管褶皱的固有形成方式，褶皱的内外波瓣都恰好出现在内外开槽处，说明在一定条件下内外交替开槽方式可控制圆管的变形模式，在3个褶皱形成过程中，撞击力相对稳定，在褶皱形成完成后，圆管进入压实阶段，撞击力迅速地上升。由图10(d)和图11(d)可知，方式3的外波纹诱导使圆管形成了较差的变形模式，这可能是由于波纹诱导的波长为20 mm，圆管固有波长为40 mm，在形成褶皱的过程中，内外表面屈曲不一致导致整个圆管圆周褶皱形成混乱，在上下2个褶皱形成后，中间褶皱挤压力变大，撞击力上升较大。由图10(e)和图11(e)可知，方式4的诱导结构也改变了圆管褶皱波长，圆管塑性铰的形成位置在正弦波纹的波峰波谷处，褶皱数量同波纹数一致为6个，波纹管经历了3个阶段的变形，初始峰值力阶段，稳定折叠变形阶段和密实化阶段[14]。在稳定折叠变形阶段，撞击力基本趋向于理想矩形形状，但在密实话阶段，撞击力上升较大。

(a) 初始圆管；(b) 方式1；(c) 方式2；(d) 方式3；(e) 方式4

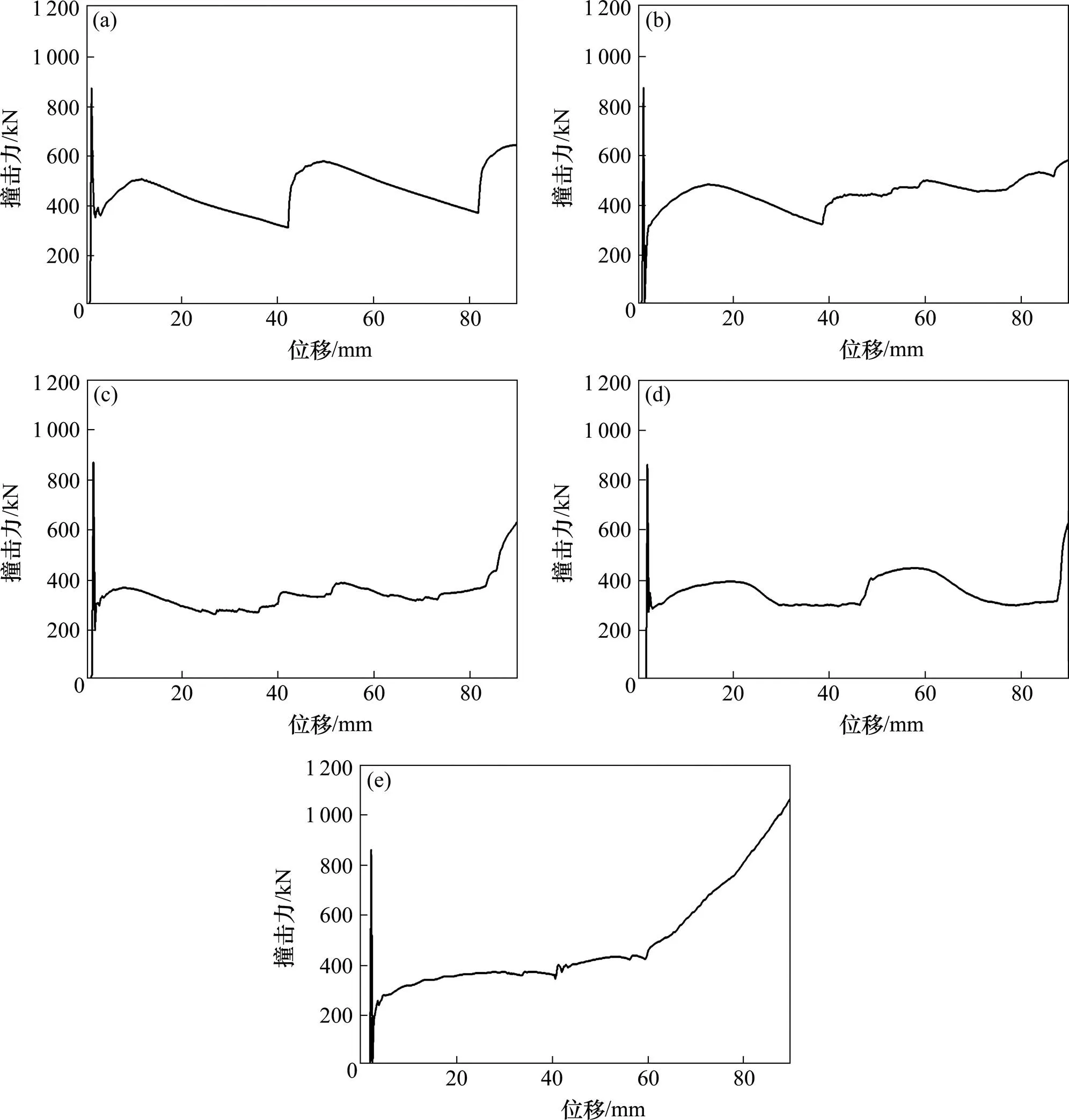
(a) 初始圆管；(b) 方式1；(c) 方式2；(d) 方式3；(e) 方式4

3.2.2 诱导结构对吸能特性的影响

在动态冲击条件下，折叠式压溃管的有效压缩量和有效吸能量为撞击力急剧上升之前的压缩量和吸能量，为量化不同诱导结构下圆管的吸能特性，以下评价系数都为各个圆管撞击力急剧上升之前的有效系数。本文选取有效比吸能SEA (Specific Energy Absorption)、有效平均撞击力m(Mean Crushing Force)和有效载荷波动系数ULC(undula- tion of load-carrying capacity)。比吸能的定义为：

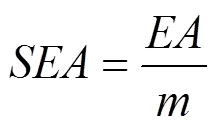
式(1)中：为撞击过程中的总吸能量；e为撞击力急剧上升之前的有效变形压缩量；为圆管质量，圆管比吸能越大说明其吸能性能越好。有效平均撞击力的定义为：

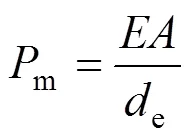
有效平均撞击力体现了圆管单位长度的吸能量，m越大，说明压溃圆管单位长度吸能效率越高。根据文献[17]，有效载荷波动系数的计算公式如下：

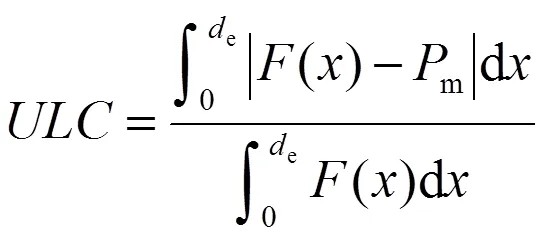
ULC越小，说明撞击力−位移曲线的撞击波动越小，曲线越接近理想的矩形曲线，圆管越接近理想的吸能结构。根据图11初始圆管和4种不同表面诱导结构下圆管的撞击力−位移曲线比较，表2为不同诱导结构下的压溃圆管的各个有效吸能评价参数值。

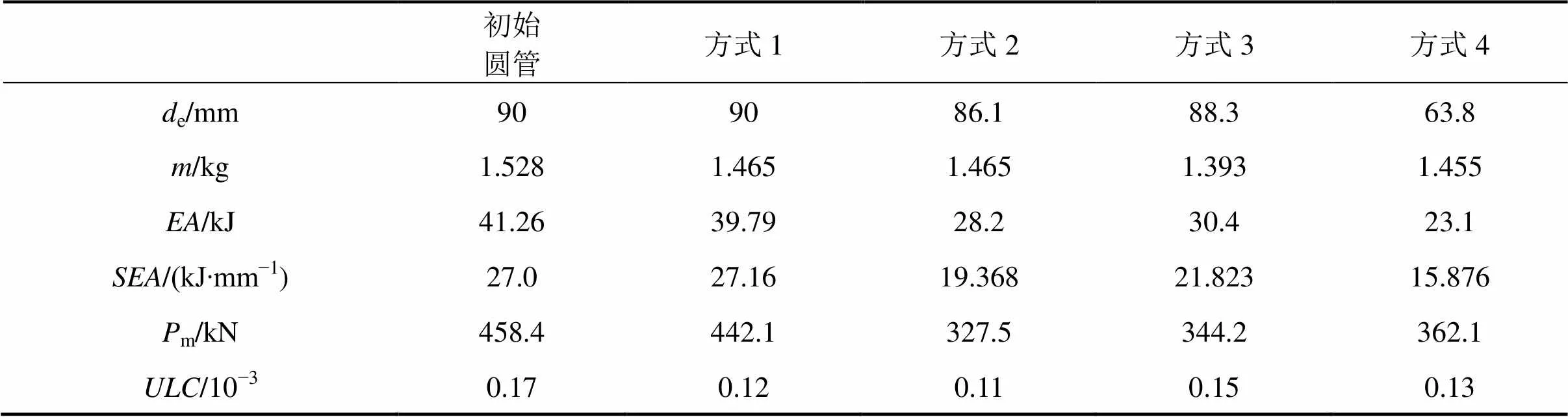
表2 原圆管和4种不同诱导结构下圆管的吸能特性参数值

由图12和表3可知，初始圆管和方式1诱导结构下的圆管的有效压缩距离为圆管的实际压缩距离，方式2，方式3和方式4诱导结构下的圆管，由于压实有撞击力骤升阶段，所以有效压缩量小于圆管实际压缩距离。5种圆管中，诱导结构1的圆管有效比吸能最大，方式2，3和4下的圆管由于诱导结构的存在，有效比吸能和有效平台力都下降很多，这也解释了它们压缩完一定距离后，撞击力迅速上升现象。就有效载荷波动系数而言，4种诱导结构下的ULC与初始圆管相比分别减少了29.4%，35.3%，11.8%和23.5%，说明在折叠阶段，4种诱导结构都能使圆管撞击力-位移曲线变平稳。但是方式2，3和4诱导结构下的圆管由于折叠阶段之后的撞击力骤升，整体载荷波动系数会比初始圆管大很多。

由以上分析可知，诱导结构1外部开槽诱导能提高圆管的比吸能，减小撞击力−位移曲线波动系数，同时撞击平台力与初始圆管基本相当，此诱导结构可为折叠式压溃管的吸能特性优化提供参考。

4 结论

1) 在冲击速度为2.7 m/s的工况下，通过非线性有限元软件LS-DYNA对折叠式压溃管进行有限元仿真，探究折叠式压溃管的变形模式和吸能特性，进行与有限元仿真相对应的动态冲击实验，实验结果与有限元仿真的变形模式和撞击力−位移曲线基本吻合。

2) 通过有限元仿真可以发现，吸能结构动态冲击前的预压缩能够有效缩短吸能圆管的褶皱波长，但对其变形模式和撞击平台力大小基本没有影响。圆管表面诱导结构对吸能结构的变形模式和吸能特性有一定影响。内外表面交替刻槽和内外波纹管诱导结构能完全改变和控制吸能圆管的变形模式，外表面开槽诱导对吸能圆管的褶皱波瓣形状有一定影响，外表面波纹诱导会使吸能圆管呈现一定的非对称变形。在撞击力上升之前的折叠阶段，以上4种诱导结构分别能使撞击力−位移曲线的波动系数减少了29.4%，35.3%，11.8%和23.5%。

3) 整体而言，与初始圆管相比，只有外部开槽诱导下的圆管比吸能增大，载荷波动系数减小29.4%，撞击平台力与初始圆管基本相当。此诱导结构可为折叠式压溃管吸能特性优化提供基础。

[1] Alexander J M. An approximate analysis of the collapse of thin cylindrical shells under axial loading[J]. The Quarterly Journal of Mechanics and Applied Mathematics, 1960, 13(1): 10−15.

[2] Wierzbicki T, Bhat S U, Abramowicz W. Alexander revisited-a two folding elements model for progressive crushing of tubes[J]. International Journal of Solids & Structures, 1992, 29(24): 3269−3288.

[3] Singace A A, Elsobky H, Reddy T Y. On the eccentricity factor in the progressive crushing of tubes[J]. International Journal of Solids & Structures, 1995, 32(24): 3589−3602.

[4] Daneshi G H, Hosseinipour S J. Elastic–plastic theory for initial buckling load of thin-walled grooved tubes under axial compression[J]. Journal of Materials Processing Technology, 2002, 125−126(36): 826−832.

[5] Hosseinipour S J, Daneshi G H. Energy absorption and mean crushing load of thin-walled grooved tubes under axial compression[J]. Thin-Walled Structures, 2003, 41(1): 31−46.

[6] Hosseinipour S J. Mathematical model for thin-walled grooved tubes under axial compression[J]. Materials & Design, 2003, 24(6): 463−469.

[7] WEI Y, YANG Z, YAN H, et al. Proactive regulation of axial crushing behavior of thin-walled circular tube by gradient grooves[J]. International Journal of Mechanical Sciences, 2016, 108−109: 49−60.

[8] YANG Z, YU Y, WEI Y, et al. Crushing behavior of a thin-walled circular tube with internal gradient grooves fabricated by SLM 3D printing[J]. Thin-Walled Structures, 2017, 111: 1−8.

[9] Salehghaffari S, Rais-Rohani M, Najafi A. Analysis and optimization of externally stiffened crush tubes[J]. Thin-Walled Structures, 2013, 49(3): 397−408.

[10] SUN G, XU F, LI G, et al. Crashing analysis and multi-objective optimization for thin-walled structures with functionally graded thickness[J]. International Journal of Impact Engineering, 2014, 64(64): 62−74.

[11] Rajabiehfard R, Darvizeh A, Alitavoli M, et al. Experimental and numerical investigation of dynamic plastic behavior of tube with different thickness distribution under axial impact[J]. Thin–Walled Structures, 2016, 109: 174−184.

[12] CHEN D H, Ozaki S. Numerical study of axially crushed cylindrical tubes with corrugated surface[J]. Thin-Walled Structures, 2009, 47(11): 1387−1396.

[13] Eyvazian A, Habibi M K, Hamouda A M, et al. Axial crushing behavior and energy absorption efficiency of corrugated tubes[J]. Materials & Design, 2014, 54(2): 1028−1038.

[14] LIU Z, HAO W, XIE J, et al. Axial-impact buckling modes and energy absorption properties of thin-walled corrugated tubes with sinusoidal patterns[J]. Thin-Walled Structures, 2015, 94: 410−423.

[15] WU S, LI G, SUN G, et al. Crashworthiness analysis and optimization of sinusoidal corrugation tube[J]. Thin-Walled Structures, 2016, 105: 121−134.

[16] 王青春, 范子杰. 利用Ls-dyna计算结构准静态压溃的改进方法[J]. 力学与实践, 2003, 25(3): 20−23. WANG Qinchun, FAN Zijie. The way to improve structure’s quasi-static compression with Ls-dyna[J]. Mechanics and Practice, 2003, 25(3): 20−22.

[17] XIANG Yanfei, WANG Min, YU Tongxi, et al. Key performance indicators of tube and foam-filled tubes used as energy absorbers[J]. International Journal of Applied Mechanics, 2015, 7 (4): 1550060.

(编辑 阳丽霞)

Dynamic crashworthiness analysis of fold-collapse tube with different induced structures

LIANG Yu, YAO Song, XU Ping, ZHOU Zhipeng

(Key Laboratory of Traffic Safety on Track of Ministry of Education, School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China)

The FE model of fold-collapse tube with pre-compressing structure was established in this paper. The deformation mode of tube was axisymmetric and the crushing force curve was obtained. Dynamic impact experiment was conducted and the result of FE simulation and experiment are in good agreement, which validates the correctness of FE model. It is found that the pre-compressing structure can reduce the first wrinkle’s wavelength but have little influence on deformation mode and crushing force. Four different induced structures were set on the circular tube, which are grooves on external surface, grooves on internal and external surface, corrugation on external surface, and corrugation on internal and external surface. The induced structures with grooves on internal and external surface and corrugation on internal and external surface can change and control deformation modes of circular tube. The grooves on external surface affect the shape of wrinkle lobes and the corrugation on external surface makes the deformation mode asymmetric. In whole fold process, compared with the initial tube, only the induced structures with grooves on external surface can increase the SEA (Specific Energy Absorption), decrease the ULC(undulation of load-carrying capacity) by 29.4% and maintain the fairly mean crushing force at the same time. Therefore, it can be the optimization foundation of the fold-collapse circular tube to realize better crashworthiness characteristics.

fold-collapse tube; pre-compressing; induced structure; undulation of load-carrying capacity

10.19713/j.cnki.43−1423/u.2018.08.022

U270

A

1672 − 7029(2018)08 − 2072 − 11

2017−05−20

国家自然科学基金资助项目(51275532，U1334208)；“十二五”国家科技支撑计划项目(2015BAG13B01)；“十三五”国家重点研发计划项目(2016YFB1200602-33)

姚松(1975−)，男，湖北公安人，教授，从事轨道交通安全研究；E−mail：song_yao@csu.edu.cn