寓数于形以形解数—谈小学数学中的数形结合教学

吴秀敏

（山西省繁峙县实验小学，山西繁峙 034300）

引 言

纵观2011年版的小学数学课程改革标准的要求可以发现，该标准首次将数学思想方法的渗透作为小学数学教学活动开展的基本目标。所谓的数学思想方法，主要是指学生在数学教学活动参与中能在已有的数学认知基础之上总结概括出的一种观点，并借助该观点来自主地解决数学问题的途径或策略。数学思想方法所包含的内容多种多样；其中，数形结合这一思想方法是最常用的。因为数学本身就是一门以抽象的数和直观的形为基础的学科。在小学数学教学活动开展中，对于数学认知能力有限的小学生来说，抽象的数字、概念等是难以理解的，此时教师可以借助直观的形来帮助学生理解；此外，教师还可以借助具体的数赋予“抽象的”形以实际意义，借此加深学生对图形的理解。由此可以看出，在小学数学教学活动开展中，教师借助数形结合这一思想方法有助于学生理解数学、应用数学，为他们数学学习能力的提升打下坚实的基础[1]。在本文中，笔者主要从以形解数、寓数于形这两个方面来分析如何在小学数学教学活动开展中实现数学结合思想方法的渗透。

一、以形解数

（一）巧用实物

通过对心理学的有关研究加以分析，并结合对所执教班级的小学生进行观察，笔者发现，大部分学生的思维在小学阶段正处于由形象向抽象过渡的阶段；且其形象思维发挥着主要的作用。数学本身就是一门极具抽象性的学科，这一点是毋庸置疑的。在小学数学教学活动开展中，量与量之间的关系问题大量存在，抽象的数、数量关系等使得以形象思维为主的小学生难以对其有深刻的理解，甚至在大量抽象知识的堆积下，学生会对数学学习丧失兴趣。对此，教师在组织教学活动的时候，可以立足教学实际内容，借助多样化的手段将抽象的数、数量关系等转化为直观的符号或图形，使学生在直观的观察中加深对这些抽象的数的理解。

笔者在组织数学教学活动的时候，发现大部分学生在教师的讲解下，对体积的概念有一定的理解，并能对其进行熟练的识记；但是，在具体的实物判断过程中，却无法灵活地将所学到的与体积有关的内容应用其中。造成这一问题的原因主要是教师在教学活动开展中没有将“体积单位”与具体的实物建立一个直观的联系。对于数学认知有限的小学生来说，多大的物体是lcm3是无从可知的。针对这一情况，为了加深学生对“体积单位”的认知，笔者在组织教学活动的时候，会先利用多媒体向学生播放乌鸦喝水的画面，他们在直观的画面观看中，会不自觉地建立起与体积有关的表象认知；在此基础之上，笔者会引导学生调动已有的知识经验，结合所观看的画面自主地探究出体积的概念，实现由具体到抽象的过渡。在学生自主探究体积概念的过程中，笔者会给予指导，帮助他们建立深刻的体积认知；最后，笔者立足学生所建立的体积认知，向他们呈现生活中常见的物品，使他们在实物的观察下，建立起1cm3，1dm3和1m3表象。

（二）巧用线段

通过上文对数形结合思想方法的介绍可以看到，该思想方法最大的特点就是实现抽象问题的简单化。数学问题的简单化得以实现的前提则是借助简单的图形将抽象的数学知识直观地呈现在学生面前，使他们在简单图形的辅助下有效地把握概念的本质。数学简单图形的类型多样，其中笔者最常使用的当属线段图，尤其在应用题解决中，线段图的使用可以有效地帮助学生解决问题。

以小学数学中最常见的“植树问题”为例：现在有一条长度为100m的小路，要在该小路的一旁种上树，每棵树之间间隔5m（路的两端也需要栽上树），试问这条路上一共要栽种多少棵树？这一问题看似很简单，但是其中却蕴藏着一个较为重要的数学知识，即两端都要栽树，所栽树的棵数比间隔数多1。对于这一数学模型，学生在有限的数学思维能力的作用下难以探究出来。此时，笔者则引导学生借助线段图的方式直观地探究该模型，如图1所示：

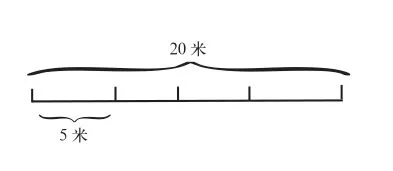
图1

在直观的线段图的作用下，学生可以准确地找出题目中所给出的数量关系；甚至可以在图形和数量关系的双重作用下自主地探究出数学模型。在加深学生对该类问题理解的基础上，为其灵活地运用模型解决其他问题打下坚实的基础。

二、寓数于形

寓数于形其实就是教师通常所说的以数解形，即在数学教学活动开展中，引导学生借助代数知识来解决较为复杂的几何问题。在实现以数解形的过程中，笔者一般会采取借助数的特点，渗透模型思想这一方法。

2011年版的小学数学课程标准中新增了模型思想这一内容。所谓的数学模型主要是指立足特定的研究问题，借助形式化的数学语言对所要研究的内容加以抽象、概括，将其主要的特征、关系等以数学结构的方式呈现出来。在数学教学活动开展中，教师一般会利用字母、数字等来建立关系式、表达式等，这些式子、图形等其实就是平时所说的数学模型。

在组织《长方体与正方体体积》这一内容教学的时候，在传统的以照本宣科为主的教学方式下，大部分教师会直接将长方体、正方体的体积公式呈现在学生面前；而学生只能借助死记硬背的方式来识记这些公式，对这些公式的来源知之甚少。这就限制了学生对其进行灵活的运用。对此，笔者在组织该内容教学的时候，会先让学生自主地选择几个体积为1cm3的正方体实物，然后将所选择的正方体摆成长方体，并以表格的形式将所选择的正方体的个数以及其体积进行记录。学生可以在对体积概念及其意义理解的基础上，通过简单的计算来实现记录，在明确的数字观察下，学生会发现：正方体的个数其实就是长方体的体积。在学生发现1cm3正方体的体积与长方体体积关系的基础之上，笔者再次对其加以引导，计算所摆成的长方体的长、宽、高，以及三者之间的乘积与其体积之间的关系。在这样的引导下，学生可以自主地探究出长方体的体积公式。在这样的数学体验过程中，学生经过亲身的探究自然会加深对长方体、正方体体积公式的理解，为其灵活地运用公式解决实际问题打下了坚实的基础。

除了以上所提及的借助数的特点，渗透模型思想方法之外，教师还可以灵活地运用数学公式、定理等，帮助学生掌握图形结构之间的关系。

结 语

总之，在小学数学教学活动开展中，教师除了将基础的数学知识呈现在学生面前之外，还要将数学思想方法渗透其中，使他们在数形结合思想方法的作用下，加深对基础知识的理解，掌握数学学习的方法，从而为他们灵活地运用所学奠定坚实的基础。