一种计算机无线通信信号调制识别方法*

杨雯迪

（辽宁师范大学 计算机与信息技术学院，辽宁 沈阳 110200）

0 引 言

如今，将计算机技术与无线通信技术结合的计算机通信技术广泛应用在军事、民用等领域，在现代通信中有着重要作用。与传统的通信技术相比，计算机无线通信技术通信能力较强、包含信息量大且适应时空转换，在实现智能通信、实时检测等应用方面前景广阔[1]。在计算机无线通信体系中，结合计算机技术，对无线通信信号的检测及其调制类型的自动识别是当前的研究热点，而以计算机技术为基础的无线通信信号自动识别研究意义重大。

为实现无线通信信号迅速、精确的识别，针对信号特征提取，部分研究人员提出了基于信号瞬时相位和频率、小波变换、希尔伯特黄变换等计算机技术的特征提取方法[2]，而针对计算机分类器的设计，为改善调制识别的效率和准确率，提出了选择树分类器、人工神经网络分类器和支持向量机分类器[3]等。

本文拟基于一种GA-LSSVM的计算机调制识别技术，构造一种新的无线通信信号分类器，以使调制信号的识别分类更加准确、高效。

1 模式识别

1.1 遗传算法

遗传算法（GA）是一种进化算法，基本原理是仿照自然界中“物竞天择、适者生存”原则，将问题参数进行编码，采用迭代方式对染色体进行选择、交叉以及变异等操作，通过交换不同染色体信息，实现对目标参数的优化选择[4]。

采用遗传算法对最小支持向量机参数[5-6]进行优化，算法基本步骤如下：

（1）随机产生搜索空间内100个个体s1,s2,…,s100组成初始种群S，置代数计数器t=1；

（2）计算S中每一个个体si的适应度fi=f (si)；

（3）计算概率：

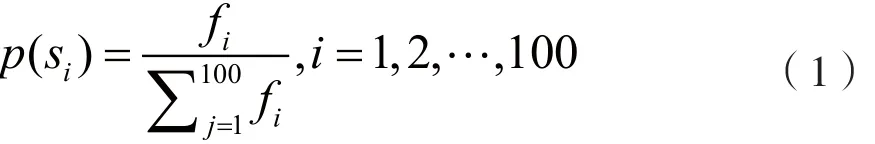
根据上述概率分布公式，依次从S中随机选取个体并进行染色体复制，复制100次，使用新的染色体群体代替原来群体，得到新群体S2。

（4）根据交叉率Pc选择参加交叉的染色体数C，从S2中随机选出C个染色体配对进行交叉操作，使用新的染色体代替原染色体群体，得到群体S3。

（5）根据变异率Pm、变异次数m，从S3中随机选出m个染色体进行变异操作，并使用新的染色体代替原染色体群体，得到群体S4。

（6）重复上述步骤，直至得到最优解。

图1为遗传算法实现流程。

1.2 支持向量机

最小二乘支持向量机（LSSVM）主要针对二分类问题，基本思想是采用结构风险最小化原则，构造满足条件的分类平面，通过将次平面作为决策面，保证分类正确的同时，使得两类样本之间的间距最大化。

LSSVM具有以下优点：

（1）有效性：是最好的解决实际问题的方法之一；

（2）鲁棒性：不需要微调；

（3）计算简单：方法实现利用简单的优化技术；

（4）理论完善：基于VC推广性理论的框架。

图1 遗传算法实现流程

在支持向量机x(i)和输入空间抽取的向量x之间的内积核概念是算法的关键，其体系机构如图2所示。

图2 支持向量机架构

K为核函数，向量机的复杂度因核函数的不同存在差异。经常使用的核函数有以下几种[7]：

（1）多项式核函数

（2）径向基核函数

（3）多层神经网络正切双曲线核函数

式（1）、式（2）和式（3）中：

式（3）中，q、δ、v、c都是核函数参数。

核函数广泛应用于目标预测等众多领域，其优势表现如下[8]：

（1）在进行非线性变换时，φ(x)参数值、形式可未知；

（2）空间样本数据映射至高维特征空间的方式取决于核函数，不同类型的核函数和对应参数，对分类性能有不同的影响；

（3）核函数矩阵不受空间维数限制，可用于解决高维数据输入问题，有效解决维数灾难问题，降低计算复杂度；

（4）核函数方式兼容性较好，可与不同方法进行融合生成混合方法。

本文设D={(xk, yk)|k=1,2,…,N}。其中，xk∈R为不同位置任务选取最优半径时对应的竞争度取值，yk∈R是最优半径对应的最低定价。在权值ω空间中，最小二乘支持向量机解目标函数如下：

约束条件为：

定义拉格朗日函数为：

式中，拉格朗日乘子αk∈R。对式（8）进行优化，即对w、b、ek、αk求偏导，令结果等于0，则最终可得到矩阵方程如下：

式中：

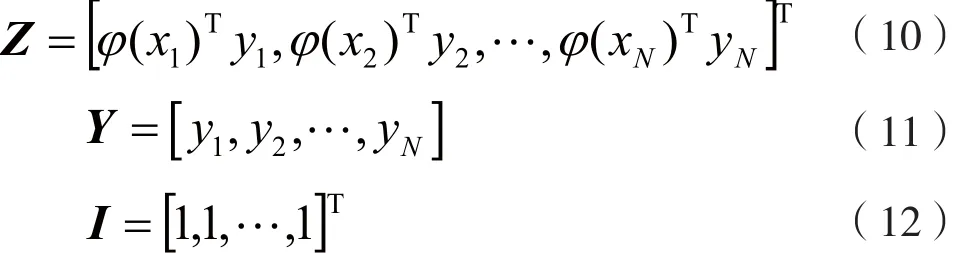
将Mercer条件带入Ω=ZZT中，有：

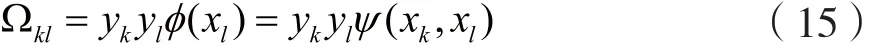
进而可实现对式（7）和式（8）的求解。此外，本文选取最小二乘支持向量机的决策函数：

2 数字信号调制识别模型

2.1 特征参数提取

在对通信信号进行识别时，通过对待识别样本信号进行特征参数提取，可有效降低数据量对信号识别的影响，通过将高维样本数据转换至低维空间，可有效降低数据的空间维数[9]。特性参数的选择方法不同、估计方法不同，分类算法性能也不同。

对不同特征参数的评价可从以下方面进行：特征参数是否对调制信号的特点进行显著表征，特征参数可否对噪声干扰进行有效抑制。本文从待识别信号的频谱、信号复杂度以及瞬时信息等中选择不同特征参数，构成样本信号的特征集。

（1）零中心归一化顺势幅度谱密度最大值γmax：

式中，Ns表示信号采样点数目，a(i)为信号瞬时幅度，ma为瞬时幅度取平均值，an(i)表示采用归一化处理之后的瞬时幅度，acn(i)表示采用中心归一化处理后的瞬时幅度。通过对瞬时幅度进行归一化处理，可消除信道增益对特征参数的干扰。信号的特征参数γmax表征幅度变化信息，可用来区分（FSK、4PSK）和（ASK、2PSK、16QAM）。

（2）零中心归一化瞬时幅度绝对值标准差：

2PSK信号调制过程中，振幅并非完全对称。特征参数δaa表征信号幅值绝对值的变化程度，可区分2ASK和2PSK信号。

（3）振幅包络的标准差E：

4PSK、16QAM载波幅度有较多的取值，与2ASK和2PSK信号相比，拥有较大的瞬时幅度波动和幅度包络方差。采用特征参数E对信号瞬时幅度的波动程度进行说明，可有效识别2ASK、4ASK、2PSK和16QAM。

（4）特征参数R：

其中，μ表示信号振幅包络平均值，δ表示信号振幅包络平方标准差。特征参数体现了信号振幅包络的波动情况，区分16QAM和4ASK。

（5）非弱信号段中心归一化瞬时频率绝对值标准差 σaf：

式中，at表示信号幅度的阈值，常用来对非弱信号段进行判别，取值1；C为采用点中处于非弱信号段的样本数目；fN(i)表示非弱信号段归一化处理后的瞬时频率。特征参数σaf表征信号中的绝对频率信息状态，可用于判别2FSK和4FSK。

（6）信号盒维数DB：

盒维数起源于分形理论，可对信号的不规则程度、复杂度以及几何尺寸作出准确描述。数字调制信号是一个随时间依次变化的规则序列，特征参数可用来区分4PSK与2FSK、4FSK。

2.2 基于GA-LSSVM调制识别

利用GA-LSSVM分类器对调制识别的样本信号特征集合进行识别分类，具体显示步骤如下。

步骤1：按照特征提取公式，分别提取7种数字调制信号的相关特征参数，选择调制识别样本信号特征集合为LSSVM分类器输入数据。

步骤2：选择合适的核函数。

步骤3：采用遗传算法对SVM分类器参数C和σ进行寻优，找到最优解后带入SVM模型，构成GA-LSSVM分类器。

步骤4：将训练样本数据输入GA-LSSVM分类器，实现分类器训练过程，定位最优分类超平面，构建GA-LSSVM分类模型；将样本数据集带入训练完成的分类模型，输出结果是各调制信号的类型。

3 仿真结果与分析

在分布高斯噪声的信号中，选择2ASK、4ASK、2FSK、4FSK、2PSK、4PSK和 16QAM等 待识别信号，提取对应的特征参数构建样本集，利用GA-LSSVM分类模型对不同数字信号进行识别分类。

调制信号参数设置如下：符号速率ra=1，采样频率fs=200 kHz，载波频率fc=20 kHz，FSK信号的频偏df=10 kHz，在信噪比-5～10 dB内，每隔5 dB取样一次，每次取样数目为400，每个样本包含50个码元。

设置GA算法的参数如下：搜索空间范围[0.001，1 000]，种群规模100，迭代次数为100，交叉概率为0.4，变异概率为0.2。为进一步验证本文算法识别性能，不同算法测试相关结果如图3所示。

图3 不同算法准确度对比

可见，在核函数相同的条件下，将本文测试结果与粒子群优化算法（PSO-LSSVM）、扩展蜂群优化算法（EPSAB-LSSVM）以及最小二乘支持向量机（LSSVM）对比，发现在方正的各信噪比点上，基于遗传算法的最小二乘支持向量机分类误差均小于10%，分类准确性达到90%以上，分类优势明显。

4 结 语

构建新型的计算机无线通信分类器，为无线电数字信号调制识别提供了新的方法。首先通过GALSSVM算法优化选取了SVM分类惩罚因子和核函数参数，提升分类器效率，在不同信噪条件下，评估GA-LSSVM识别分类器的性能。对七种数字调制信号进行计算机识别仿真结果显示，噪声环境不同时，与其它识别分类器相比，GA-LSSVM分类器性能更优，且当信噪比大于0 dB时，分类器的分类误差可控制在10%以下。