两种概率分析方法的混凝土疲劳寿命模型比较

(郑州工业应用技术学院 河南 新郑 451100)

引言

自从1829年德国采矿工师W.A.J.Albert提出第一个疲劳问题研究报告以来，人们对疲劳问题的研究已经持续将近两个世纪，但仍有许多问题困扰着人们。其中，因混凝土自身为非均质多相材料，在静力作用下其相关性质的离散度就较大，而且在疲劳荷载等动力作用下，其相关性质的离散度就更大，由此产生一系列难题。如试件制备方法、试验方法、试验数据处理方法等。针对混凝土疲劳问题，主要对一定强度等级的混凝土，在一定疲劳应力水平下的S-N曲线、ε-N曲线、σ-ε曲线等特征参数进行试验研究，然后再针对试验数据进行相关理论分析。在对材料诸多疲劳行为的研究中，材料的疲劳寿命曲线是预测结构疲劳寿命和进行结构抗疲劳设计的基础。目前，常用的材料疲劳寿命曲线有两类：应力-寿命(S-N)曲线和应变-寿命(ε-N)曲线。材料的疲劳寿命曲线的表述形式可采用表格形式或表达式形式，而在理论研究和工程应用中，为准确反映物理规律以及使用方便，通常采用表达式形式。譬如，因混凝土试件静载强度的离散性导致疲劳应力水平S的离散性加大，又进一步导致疲劳寿命N的离散性更大；类似的参数还有应变、弹性模量等，其离散性均为逐步放大。因此，S-N等曲线的这种固有缺陷是无法从根本上消除的，这就需要利用相关数学手段对试验数据进行有效分析，来提高混凝土疲劳寿命的预测精度。在1939年之前，对混凝土疲劳寿命的概率分析，基本上都是采用对数分布[1-3]或对数正态分布[4]。但在1939年，瑞典人Weibull提出了一种描述材料疲劳强度的分布模型，即Weibull分布模型[5,6]。该模型参数能较好地反映随机荷载下机械产品及其零件的疲劳寿命和疲劳强度。而在1956年，Leiblein和Zenlen在对滚珠轴承的疲劳试验分析时即用到了Weibull分布。此后，Weibull分布便被广泛应用于零部件的疲劳分析，以及后来的可靠性分析之中。经过多年来国内外广大学者[7-9]的深入系统地研究，不仅证明了混凝土疲劳寿命既服从对数正态分布又服从两参数Weibull分布，并通过概率函数研究了这两种函数的逼近性；而且基于工程可靠性的Weibull分布模型，对混凝土的疲劳寿命预测更加合理。为此，本文通过相关文献中的试验数据，对提高疲劳寿命预测精度的方法进行了系统分析，结果证明该方法是正确的。

一、结构可靠度理论[10-12]

结构的可靠性是指结构在规定的时间内，在规定的条件下，完成预定功能的能力。假设结构或构件能完成预定功能(Z≥0)的概率称为可靠概率，亦称为可靠度(ps)，而不能完成预定功能的概率(Z<0)，则称之为失效概率(Pf)。又假设功能函数(Z)仅与作用效应(S)和结构抗力(R)两个基本变量有关，则结构功能函数即为

Z=g(R，S)=R-S

(1)

当R、S均服从正态分布，且相互独立时，则结构的失效概率为

(2)

失效概率为

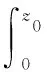
(3)

其中，z0表示结构的极限功能，如强度、挠度、裂缝极限宽度等极限状态。

(一)对数正态分布统计理论

在疲劳理论中，常用的对数正态分布分布形式为Y=lg(X)，其对数正态分布分为

基本变量X的概率密度函数为

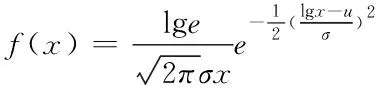
(4)

对数正态分布的累积分布函数为

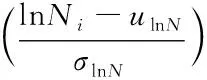
(5)

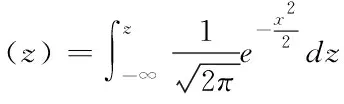
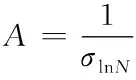
则Y1=AX-C

(6)

(二)Weibull分布统计理论

在某一特定循环荷载作用下，混凝土疲劳寿命N服从一定的分布规律，用Weibull函数可表示为

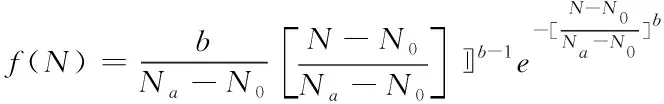
(7)

其中，N0—最小寿命参数；Na—特征寿命参数，36.8%存活率下的安全寿命；b—Weibull形状参数。

可得

(8)

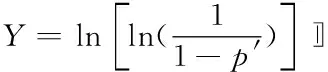
可得:Y=bX-α

(9)

式(9)即为可检验试验数据是否符合两参数的Weibull分布判断标准。若试验数据线性回归表明Y与X之间线性关系良好，则说明数据符合两参数威布尔分布。

二、混凝土疲劳寿命的概率分析

以文献[13]中的试验数据为例，利用上文推导结果对混凝土疲劳寿命进行概率分析结果并以Xi=lnNi为横坐标，Y=φ-1(F(lnNi))为纵坐标，则其线性回归检验结果分别如图1中各分图所示。

(a1)Smax=0.85

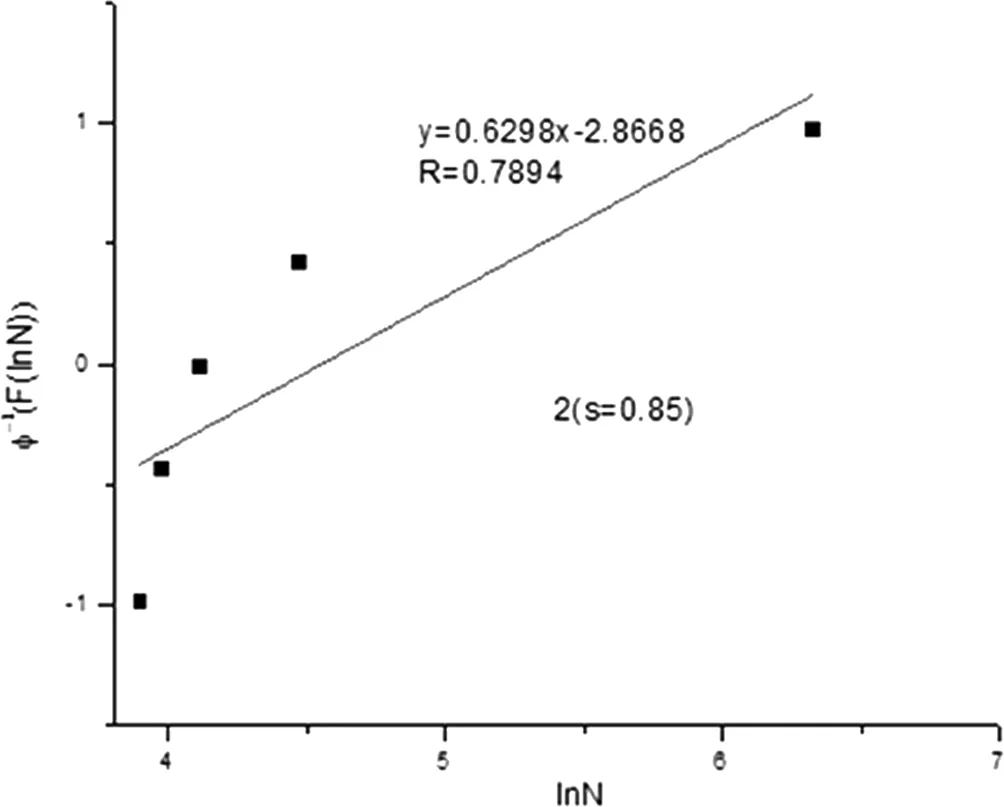
图1 混凝土疲劳寿命的对数正态分布线性回归检验

三、结果分析

由图1的对数正态分布线性回归结果可知，函数Y=φ-1(F(lnNi))和Xi=lnNi在各应力水平下均存在良好的线性关系。并在失效概率p=50%的条件下，按文献[14]等所给出的疲劳寿命N的方程形式。

lgS=lg0.89443-0.0431lgN，

(10)

同样，由图2也可以看出，变量和变量Xi=lnNi在各应力水平下存在良好的线性关系，并在失效概率p=50%的条件下，其疲劳方程为：

lgS=lg1.0998-0.0436lgN，

(11)

由以上分析可知，混凝土疲劳寿命既服从双对数正态分布，又服从双对数的双参数Weibull分布。但对于较低应力水平条件下，混凝土疲劳寿命数据离散性较小；而在应力水平较高时，混凝土疲劳寿命数据离散性则较大；反映在不同回归结果分析中，则Weibull分布更敏感于对数正态分布，即离散性越小，则Weibull分布回归系数越大；离散性越大，则Weibull分布回归系数越小。这说明，Weibull分布能够同步反映混凝土疲劳寿命数据的可靠性，因此也更加适合对混凝土疲劳寿命分析。另一方面，在较高的应力水平下，混凝土疲劳寿命数据离散性大，反映在试验中，则需要尽力避免干扰因素，如提高配合比设计水平，提高试件成型与养护工艺，试验步骤严格遵照相关规范和规定执行等技术保障措施，努力提高试验精度；而反映在工程评估中，则需要给出较保守的评价才较为可靠。

四、结论

对数正态分布和双参数Weibull分布都可以用来描述混凝土疲劳寿命S-N方程，但后者更敏感于前者对离散数据的变化。其中，具体地用上述两种分析方法的相关系数进行评价时发现，当应力水平较高时，混凝土疲劳寿命数据离散性较大；而当应力水平较低时，混凝土疲劳寿命数据离散性则较小。因此，对于较高应力水平时，在试验过程中，应努力提高试验精度；而在工程评估中，则需偏于保守评价，否则易突发结构安全隐患。