合理转换图形，巧解线段最值——对一道中考题的解法分析与探究

☉江苏省沛县教师发展中心 甘 磊

一、考题再现及思路突破

1.考题再现

（1）试证明AC是⊙O的切线；

（2）如果点F是线段AO的中点，OE=3，试求图1中阴影的面积；

（3）在条件（2）成立的情况下，已知点P是BC边上的一个动点，当PE+PF取得最小值时，请直接写出BP的长.

图1

2.思路突破

分析：本题目为常见的几何问题，涉及到圆和三角形等基本图形，求解需结合基本的几何知识.（1）证明切线可以过点O作AC边上的垂线，如垂线为OM时，只需证明OM与圆的半径相等即可；（2）阴影部分的图形不规则，可以将其视为△AOE中切去扇形OEF获得的，即S阴影=S△AOE-S扇形OEF，然后分别利用面积公式求出△AOE和扇形OEF的面积即可完成求解；（3）在（2）的条件下求PE+PF的最小值时的BP长，实际上就是求点P的具体位置，可以作关于线段BC，点E的对称点G，连接FG，则此时FG的长度就是PE+PF的最小值，FG与BC的交点就是满足条件的点P的位置，即可求出BP的长.

解：（1）过点O作AC边上的垂线，垂足为点M，如图2.因为AB=AC，AO⊥BC，则∠BAO=∠CAO，又知OE⊥AB，OM ⊥AC， 则 △AEO≅△AMO，故OE=OM.因为OE为⊙O的半径，所以OM同为⊙O的半径，则AC是⊙O的切线.

（2）S阴影=S△AOE-S扇形OEF，其中

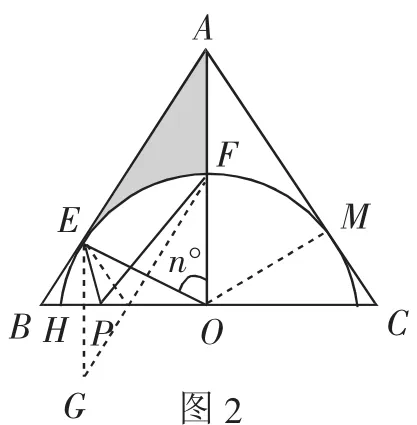
图2

（3）作点E关于线段BC的对称点G，连接EG交BC于点H，连接FG交BC于点P，可知EP=GP，由于点G、P、F处于同一直线上，则此时的PE+PF最小.在Rt△EHO中，EH=EOsin∠EOH=，BH=，△EHP～△FOP，则2HP=OP.又因为HO=HP+OP，可得HP=，所以BP=BH+HP=.

执行难，一直是司法实践中的困扰。生效的裁判文书得不到执行，法院判决就成了一纸空文。“用两到三年时间基本解决执行难问题”，最高人民法院铿锵有力的承诺不断转化为人民法院向执行难宣战的切实行动。探索审判权和执行权分离，改革执行体制机制，联合多部门对“老赖”进行信用惩戒，“法律白条”不断被兑现为“真金白银”。

3.考题评析

题目中是中考典型的几何综合题，图形由三角形和半圆综合而成，前两问是常规的证明和阴影面积求值问题，分别利用垂线段与圆半径相等和面积的割补法来完成，难度适中.问题第（3）问求PE+PF取得最小值时BP的长，需要确定点P的位置，属于三点之间线段的最值问题，求解时将位于不同直线上的两条线段通过轴对称的方式转化到同一直线上，从而确立了线段和的最小值，问题中隐含着研究线段和的最值模型，下面将深入探究.

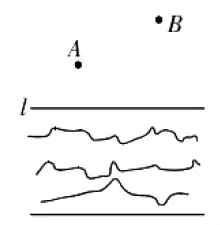
图3

二、最值研究模型的探究

1.教材模型

考题第（3）问基于几何转化思想，利用轴对称变换的方式来解决线段和的最值，其利用的理论依据是：两点之间，线段最短.该问题模型与教材中常见的水厂选址问题相类同：如图3,在一条小河的同一侧有两个村庄A和B，现要在小河边建一座自来水厂为两个村庄供水，如果要使厂址到两个村庄的供水管道最短，那么厂址应选在什么位置，试说明理由？

教材问题需要确定厂址的位置，若设厂址为P，则需要确保AP+BP的值最小，与考题在本质上是相同的，即有着同样的问题模型，具体的做法是：将小河抽象为一条直线，作点A关于线段l的对称点A1，连接A1B，与直线l相交于点P，如图4，此时AP+PB取得最小值，则点P就为自来水厂的最佳选址.

图4

2.思路分析

通过轴对称转化的方式可以确定AP+PB取最小值时点P的具体位置，可以在直线l上构造异于点P的一点M来分析：取一点M，同样连接AM和MB，在△BMA1中，BM+A1M＞A1B.因为A1B=A1P+PB，则BM+A1M＞A1P+PB，根据轴对称的特性可知，AM=A1M，AP=A1P，则有BM+MA＞AP+PB，因此异于点P的一点M获得的线段和大于点P获得的线段和，可知轴对称转化的方式可以获得线段和的最小值.

三、线段和最值问题的探究

考题的线段和问题可以等效为固定直线上一动点P，求定点E、F与动点P之间的距离和PE+PF的最小值，属于三点之间的线段和的最值问题，在动点形式和解法上都具有一定的代表性，同时近几年的中考题也都基于上述两点来进行考查，现结合2018年中考题分别从问题条件和问题解法两个方面进行变式探究.

1.问题条件变式

中考题中关于线段和的最值问题具有多种形式，上述考题中的三点具体为两点固定、一点移动，也可以将其变为一点固定，两点运动，同样求解线段和的最值，现结合考题分析.

（2018年广东广州市中考卷第23题）如图5所示，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD.

（1）利用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）.

（2）在（1）的条件下，①证明：AE⊥DE；②如果CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值.

分析：主要分析第（2）问的②，问题中的点M，N分别是AE，AB上的动点，求其最小值同样可以利用轴对称转化的方式，作点B关于线AE的对称点F，当点F、M和N位于同一直线，且FN⊥AB时，如图6，BM+MN可取得最小值，只需求得相关线段即可.

解：（2）②过点D作DP⊥AB，垂足为点P，作AD上取一点F，使得CD=DF，由1可知此时AF=AB，即点B、F关于直线AE对称，过点F作AB的垂线，垂足为N，令FN交AE于点M，连接BM，此时BM=FM，点F、M和N位于同一直线，且FN⊥AB，此时BM+MN有最小值，且BM+MN=FM+MN，分析可知，△AFN～△ADP，则=，其中AF=4，AD=6.在Rt△APD中，可以求得DP=4，则FN=，即BM+MN的最小值为

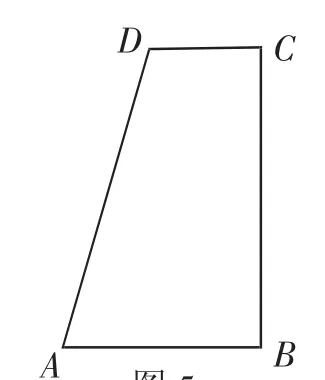
图5

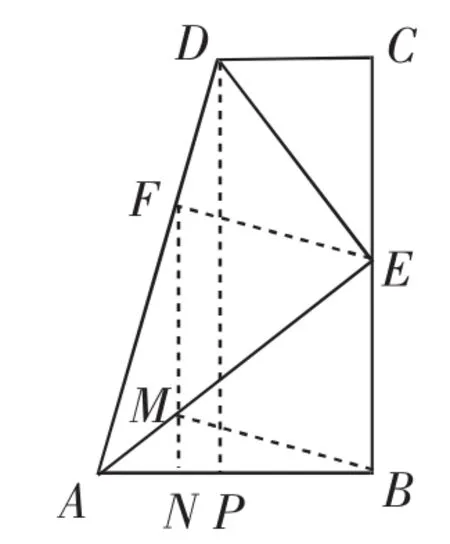
图6

上述考题同样是求三点之间线段和的最值，所不同的是存在两个动点，但同样可以依据“两点之间，线段最短”的原理，通过轴对称转换的方式来求解.在细节处理上首先选定其中一动点所在直线为顶点与另一动点的对称轴，并确定其中一动点的位置，然后连接两点确定对称轴上的另一动点的位置，从而使三点位于同一直线上，进而确定线段和的最小值.该种思路可以用于存在两动点的线段和最值求解.

2.最值解法上的拓展

对于线段和的最值问题，除了可以采用轴对称转换的方式还可以采用等效转换的方式，即通过线段长度等效的方式，将位于不同直线上的线段在同一直线上进行长度等效，转化为两点之间的距离，然后依据条件来确定线段和的最值，该种解法在考题中也有体现，下面结合考题详细讲解.

（2018年江苏无锡市中考卷第18题）如图7所示，已知∠XOY=60°，点A位于边OX上，且OA=2，过点A作AC⊥OY于点C，以AC为一边在∠XOY内作等边三角形ABC，点P是△ABC围成区域（包括各边）内的一点，过点P作PD∥OY，交OX于点D，作PE∥OX，交OY于点E，设OD=a，OE=b，则a+2b的取值范围是__________.

分析：求a+2b的取值范围，就是求EP+2DP的最值，其中点P是△ABC围成区成内的一动点，可以先对a+2b进行变形，即a+2b=2 （a +b），可以在OC的延长线上取一点H，使得EH=a，则a+b=EH+OE=OH，且三点均位于同一直线上，由于点O固定，则可以通过研究点H距O点的距离来确定线段和的取值范围.

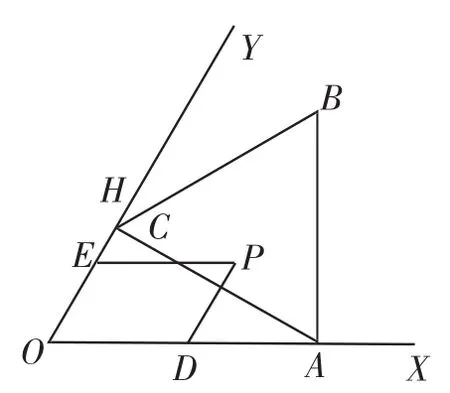
图7

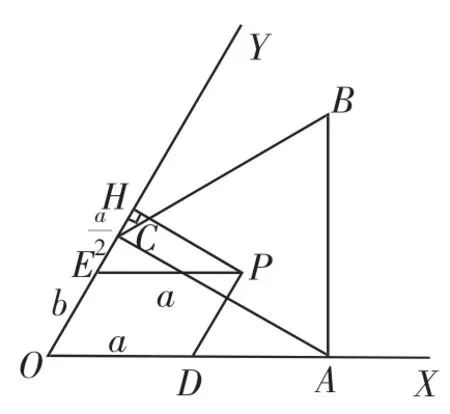
图8

解：过点P作OY的垂线PH，垂足为点H，如图8，在Rt△EHP中，∠PEH=60°，EP=a，则EH=a，a+2b=2（a+b）=2（EH+OE）=2OH，由于点P位于△ABC围城区域内，则当点P运动到C点时，OH的长度最短，即a+2b取得最小值，2OHmin=2OC=2，当点P运动到B点时，2OH的长度最长，即a+2b取得最大值，此时2OHmax=2（OE+EH）=2×（1+）=5.所以a+2b的取值范围为2≤a+2b≤5.

上述考题采用的是对线段长度的等效转化，即在同一直线上取截问题研究的两线段长，将其合并为同一线段，实现三点共线，利用的是同一直线上研究两点之间距离最值的便利性，同时在求解时对线段和进行了一定的变形处理，并用点距离来表示，使得分析问题更为直观.

四、解后思考，学习建议

线段和的最值问题，实际上几何中的动点问题，由于进行求和的两条线段位于不同的直线上，因此无论是轴对称变换法，还是长度等效转换法.实际上都是为了将两条线段转换到同一直线上，虽转换形式不同，但都是数学转化思想的利用.学习使用上述两种方式时首先需要透彻理解方法的实质，如轴对称转换，建立关于直线的对称点仅是解题的表面形式，实质上利用的是轴对称所构成的三角形全等性质；而长度等效转换则更为直接，就是在同一直线上进行的等长截取，方法的核心要素是长度等效，利用的是几何性质来完成.

对于线段的求和问题，数形结合思想贯穿解题始终，具有两种思想方法作指导：一是利用几何图形为导向直接建立问题求解的具体思路，然后利用代数方法来计算求解，即以形助数；二是基于代数对线段长度的精准表达意义来进行等效转换，该种方式主要体现在长度等效转换上，即以数解形.合理采用数形结合的解题方式，可以从抽象问题中提炼基本的模型，实现问题模型的准确分析.另外对于线段和的求值问题教材习题中有较为详细的实例，合理抽象模型往往可以获得丰富的解题经验，利于考题的分析求解.

了解问题的基本模型，理解方法的核心思想，掌握解法的求解思路是求解线段和最值问题的关键，在平时的学习中除了需要学习方法，还需要巩固基本的几何知识，灵活运用，巧妙求解.