颗粒农产品连续非淹没式水射流振动清洗过程数值模拟
2018-08-31赵章风余承彦黄剑虹
赵章风 余承彦 钟 江 黄剑虹 张 宪
(1.浙江工业大学机械工程学院, 杭州 310014; 2.浙江上洋机械股份有限公司, 衢州 324000)
0 引言
清洗是农产品加工的重要环节,不同的清洗技术将影响农产品的洗净率、清洗成本和能耗。李洪昌等[1]、蒋恩臣等[2]和韩丹丹等[3]分别利用气固两相流耦合(CFD-DEM)对风筛式清选装置振动筛分过程、内充气吹式排种器进行了数值模拟,并验证了仿真结果的准确性。刘立意等[4]利用计算流体动力学和颗粒离散元耦合的方法(FLUENT-EDEM)对稻谷通风阻力进行了数值模拟与试验。GEBREHIWOT等[5]和韩启龙等[6]分别利用CFD对风清选装置中的风场和圆柱形清洗喷嘴内外流场进行了数值模拟,通过试验验证了模拟结果的正确性。COETZEE等[7-8]通过离散元方法对挖掘机进行了数值模拟,准确预测了拉铲工作时的运动轨迹。廖庆喜等[9-10]通过离散元方法对离心式排种器进行了数值模拟、优化和验证。HONG等[11-12]对喷丸工艺进行了离散元数值模拟,得出了喷丸工艺参数和工作效果的关系。彭三河[13]研制了移动射流式莲藕清洗设备,李东[14]研制了滚筒式果蔬清洗机,孙卓等[15]研制了超声波龙胆草清洗设备。
上述研究均未涉及基于CFD-DEM对振动输送水射流连续清洗颗粒型农产品的研究。本文在理论分析基础上,通过对颗粒型农产品采用连续非淹没式水射流振动清洗过程进行CFD-DEM数值模拟,研究振动频率、振动初始角、喷嘴入口压力和方向角对洗净率的影响,从而实现高效、低耗的清洗目标。
1 颗粒和水射流的力学分析
在连续非淹没式水射流振动清洗过程中,带土颗粒型农产品在振动输送装置的作用下旋转和跳跃前进,在水射流的冲击和与振动槽的碰撞联合作用下,实现表面清洗。清洗设备如图1所示,主要由振动输送装置、水射流装置和水循环装置等组成,其中水射流装置中的喷嘴采用实心锥型结构[16],清洗系统主要参数:孔板式振动槽(长4 000 mm×宽800 mm)、清洗靶距300 mm、喷嘴间距100 mm、驱动轮偏心距10 mm、喷嘴为实心锥型结构。

图1 清洗试验平台 Fig.1 Cleaning test platform 1.振动槽 2.射流喷嘴 3.水射流系统 4.喷嘴支架 5.底座
1.1 颗粒型农产品运动分析
振动输送装置可简化为由振动槽EF和摇杆CE、HF组成的四边形机构,如图2所示。在曲柄AB和连杆BC的驱动下,绕固定支点D、G往复摆动。其中ED和FG的长度是CD和HG的2倍;AB长度为驱动轮偏心距r,驱动角速度为ω,BC与AB的长度比大于10。位于振动输送装置中的颗粒型农产品主要受重力mg、振动槽反作用力Fc、质心惯性力Fμ和摩擦转矩M等作用,ε为初始振动角。
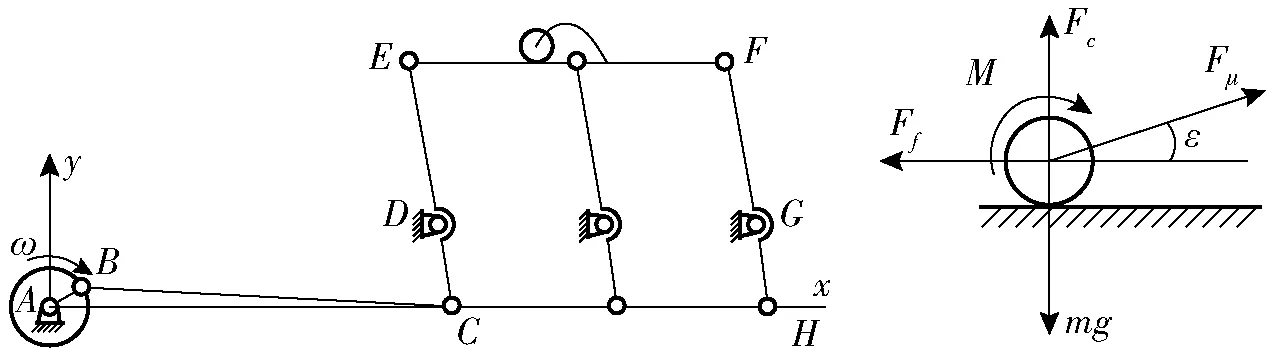
图2 振动输送机构与农产品颗粒受力图 Fig.2 Vibration conveying mechanism and agricultural product force diagram
经分析,颗粒的自转角速度ωk计算公式为
(1)
其中
(2)
式中μ——颗粒与振动槽间的摩擦因数
R——颗粒截面半径,mm
δ——颗粒滚动摩擦因数
颗粒抛离振动槽时的质心运动速度为
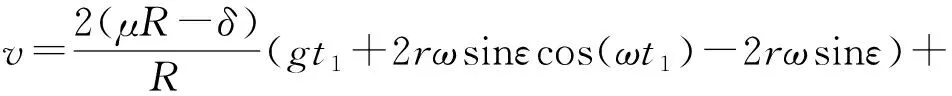
(3)
颗粒完成一次跳跃的时间t为
(4)
分析式(1)~(4)可知,颗粒抛离振动槽时的颗粒自转速度ωk,质心速度v和完成一次跳跃的时间t,与驱动轮偏心距r、振动频率f(f=2π/ω)及初始振动角ε有关。在清洗过程中,农产品被抛离振动槽时的质心速度和自转角速度越大,在空中停留的时间越长,越有利于清洗。
1.2 水射流冲击力分析
合理的喷嘴布置不仅能使水射流全面覆盖被清洗物,提高清洗质量和效率,还能减少喷嘴的数量,使清洗过程更加节水。清洗喷嘴采用横向交错布置,如图1所示,以消除清洗死角。
水射流对农产品颗粒的作用主要表现为射流冲击力FD,使土壤从颗粒表面剥离。由于水射流的雷诺数Re>103,有
(5)
v0=v-v1
(6)
FD=0.22ρA|v0|v0
(7)
式中ρ——射流液体密度,kg/m3
A——在水射流方向上农产品的投影面积,m2
v0——颗粒型农产品在水射流方向上与射流的相对速度,m/s
v1——水射流速度,m/s
p1——喷嘴入口压力,Pa
p2——喷嘴出口压力,Pa
d1——喷嘴入口孔径,m
d2——喷嘴出口孔径,m
从式(6)、(7)可以看出,水射流冲击力与相对速度v0呈正相关,当喷嘴选定以后,相对速度v0与颗粒型农产品运动速度v、喷嘴入口压力p1有关,且p1越大v0越大,射流冲击力FD越大。
除水射流冲击力FD以外,清洗效果还与水射流方向角α(水射流与振动槽平面的夹角)有关。水射流冲击力FD可以分解为正向冲击力和切向冲击力,其中正向冲击力决定了颗粒型产品表面土块能否清除,而切向冲击力决定了清洗的速度。
在连续非淹没式水射流振动清洗过程数值模拟中,颗粒型农产品(固相)与水射流(流体相)可以通过颗粒型农产品在射流方向上单位面积上的动量汇S进行耦合,即
(8)
式中FDi——第i颗粒受到射流冲击力,N
V——网格单元体积,m3
n——总颗粒数
1.3 颗粒型农产品接触力学分析
清洗过程中,带土颗粒、清洁颗粒和振动槽板相互间进行接触与碰撞,其接触力学模型如图3所示[17]。
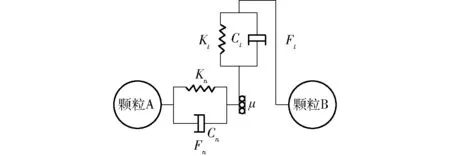
图3 接触力学模型 Fig.3 Model of contact forces
接触所产生的法向力Fn、法向阻尼力Fn,d、切向力Ft及切向阻尼力Ft,d表达式为[18]
(9)
(10)
Ft=-Stδt
(11)
(12)
式中E*——当量弹性模量,Pa
R*——当量接触半径,m
e——恢复系数
δn——法向重叠量,m
δt——切向重叠量,m
Sn——法向刚度,N/m
St——切向刚度,N/m
m*——当量质量,kg
vn——相对速度的法向分量,m/s
vt——相对速度的切向分量,m/s
由于土壤及农产品和振动槽的本构参数不同,因此在清洗过程中,各颗粒间的接触力与变形不同。
2 清洗过程数值模拟与分析
2.1 模型构建与参数设置
在农产品颗粒清洗前,一般需要经过筛分和浸泡工艺,颗粒表面大尺寸土壤破碎为小颗粒,基于生产实践,经筛分工艺后土壤颗粒最大直径一般为5 mm左右。对振动输送及清洗系统和颗粒型农产品分别建模。如图4、5所示,被清洗的带土颗粒型农产品采用农产品颗粒和土壤颗粒粘连而成,其中农产品颗粒简化为直径20 mm、长度50 mm的圆柱体,颗粒表面的土壤则可简化为直径5 mm土壤颗粒单元粘结而成,考虑到计算量及待清洗农产品实际状况,假设每个农产品颗粒表面平均粘结10个土壤颗粒。

图4 振动输送装置与水射流模型 Fig.4 Vibration conveying device and water jet model
两种颗粒模型和振动槽板的力学特性参数如表1所示。颗粒间黏结参数:切向刚度1×108N/m、法向刚度5×107N/m、切向最大应力5 000 Pa、法向最大应力2 500 Pa、接触半径2.5 mm。其他参数初始值:振动频率3 Hz、振动初始角π/5、喷嘴入口压力0.3 MPa、喷嘴方向角π/3。

图5 土壤和农产品颗粒模型 Fig.5 Models of soil particle and agricultural product

参数农产品颗粒土壤颗粒振动槽板泊松比0.40.350.3剪切模量/MPa2.616.7700密度/(kg·m-3)138026807900
2.2 洗净率的计算
随着清洗过程的进行,在振动力和水射流冲击力的共同作用下,农产品颗粒和土壤颗粒间的粘连切向力、法向力、切向力矩、法向力矩逐步叠加,当法向应力和切向应力达到最大值时,颗粒之间的黏结键被破坏,土壤颗粒与农产品颗粒分离。当附着在农产品颗粒表面的土壤颗粒全部脱离则认为该农产品颗粒清洗干净。分别统计清洗后的干净颗粒数和带土颗粒数来计算洗净率,公式为
(13)
式中a——干净颗粒数
b——带土颗粒数
2.3 数值模拟与分析
颗粒工厂设置于振动筛网入口的上方,假设颗粒工厂产生农产品颗粒数量100个、尘土颗粒1 000个,产生时间均为2 s,总仿真时间为10 s,颗粒下降速度为1 m/s,振动槽的振动方向角为π/5,振动频率为3 Hz;喷嘴水射流入射角为π/3,喷嘴入口压力为0.5 MPa。
在进行清洗过程数值模拟前,利用ICEM对水射流区域进行非结构体网格划分,然后将网格导入FLUENT中进行仿真计算,选用标准的k-ε湍流模型计算,并使得射流流场达到收敛状态,所得水射流流场速度矢量图和振动槽所受压力分布云图如图6、7所示。

图6 射流流场速度分布矢量图 Fig.6 Jet flow velocity distribution vector graph

图7 振动槽上的压力分布云图 Fig.7 Pressure distribution cloud chart on vibratory groove
分析图7可知,清洗流场呈现出典型的多股冲击射流,在振动槽表面即水射流冲击区流线发生显著弯曲,存在较大压力梯度,而且水射流速度与振动槽呈一定角度,使得水射流对被清洗颗粒同时具有正向力和切向力。从图8可以看出,振动槽表面被射流流场覆盖,无死角存在,压力基本均匀,说明喷嘴布局较为合理。经数据整理可得水射流场横截面压力和流速分布。

图8 水射流场横截面压力和流速分布 Fig.8 Cross section pressure and velocity distribution of water jet field
分析图8可知,在振动槽表面水射流场的压力与速度分布具有一定的相似性,并在喷嘴阵列外侧达到最大,而在喷嘴之间其值会有小幅下降,这是由于在离开喷嘴后的水射流具发散趋势,相邻喷嘴产生的水射流相互间存在轻微干扰,影响了压力和流速的均匀性,说明喷嘴阵列中的喷嘴并非越多越好,合理地设计喷嘴阵列,不仅有利于提高压力和流速的均匀性,使得处于不同位置的农产品颗粒受力近似相等,而且使得清洗均匀,成本和资源消耗降低。
将颗粒和振动槽模型导入EDEM进行颗粒运动模拟。由于振动槽的作用,农产品颗粒向前跳动的同时绕质心轴转动,可以使得颗粒外表面均能受水射流的作用,提高洗净率。根据模拟获得的数据,可得颗粒在输送过程中的自转角速度变化,如图9所示。

图9 输送过程中的颗粒自转角速度 Fig.9 Particle rotation angular velocity during transportation
分析图9可知,颗粒自转角速度呈周期性变化,其变化周期与振动频率一致,速度的变化由颗粒间及颗粒与振动槽的接触碰撞引起,颗粒间的接触将导致颗粒自转角速度下降,而颗粒在与振动槽的碰撞过程中,获取了能量,将提高自转角速度。这也说明在清洗过程中,过多颗粒同时清洗会提高颗粒间碰撞概率,削弱了颗粒自转角速度,将影响洗净率。
基于FLUENT-EDEM的固液耦合清洗过程数值模拟采用欧拉-欧拉法算法进行,图10分别为2、6.1、7.8、10 s时农产品颗粒(蓝色大颗粒)及土壤颗粒(红色小颗粒)随时间运动轨迹及分离状况,模型左端为清洗入口,右端为出口。

图10 清洗过程数值模拟 Fig.10 Numerical simulation of cleaning process
3 影响洗净率的因素分析
根据上文可知,影响洗净率η的主要因素有驱动轮偏心距r、振动频率f、初始振动角ε、清洗靶距、喷嘴入口压力p1和喷嘴方向角α。在驱动轮偏心距r和清洗靶距确定的前提下,基于FLUENT-EDEM多相流耦合技术通过正交试验和极差分析[19-20],研究其他因素对洗净率的影响。
3.1 方案设计与试验
试验在四因素三水平基础上进行,试验因素和水平如表2所示。
根据试验因素和水平,设计了9组试验并进行了FLUENT-EDEM清洗过程数值模拟,并基于式(13)用EDEM离散元仿真软件,对清洗后的颗粒进行比较分析并计算出对应试验方案的农产品洗净率。试验方案与模拟试验结果如表3所示。

表2 试验因素与水平 Tab.2 Test factors and levels

表3 正交试验方案及模拟试验结果分析 Tab.3 Orthogonal test program and simulation test results analysis
3.2 试验结果分析
对上述模拟试验数据进行统计分析,求出每个因素各水平的洗净率均值,得到各因素的极差如表3所示。
综合分析表3,根据极差可以得到各因素对颗粒型农产品洗净率影响:
(1)在所分析的因素中,喷嘴入口压力的极差为15,说明对洗净率最为敏感。根据各水平均值可知:随着喷嘴入口压力的增加,农产品的洗净率逐步提高。其中喷嘴入口压力为0.3 MPa时,作用在振动槽上的水射流冲击力过小,清洗效果较差;而当喷嘴入口压力为0.7 MPa时,清洗效果较好。
(2)喷嘴方向角极差为8,在诸影响因素中对洗净率敏感性仅次于喷嘴入口压力。分析各水平的均值可知存在最佳方向角,当喷嘴方向角为π/3时,满足模拟颗粒材料清洗所需的正向临界压力条件,同时具有较大的切向压力分量,所以洗净率较高且清洗效果最佳。
(3)振动槽振动频率极差为3.7,对洗净率的敏感性较小。分析各水平的均值可知,同样存在最佳值。这是因为颗粒在振动力作用下进行周期性跳跃,当跳跃周期与振动频率一致时,颗粒吸收的动能最大,跳跃次数最多,颗粒绕质心旋转快,水射流能够对颗粒外表面进行充分的清洗,有利于洗净率的提高。
(4)振动槽振动初始角的极差最小,说明对洗净率的敏感性最小。分析各水平的均值可知,也存在最佳值。振动槽振动初始角虽然对洗净率影响不大,但如果振动初始角过大,颗粒跳跃高度高,每次跳跃前进距离短,颗粒在振动槽上运动时间长,清洗效率将降低;反之洗净率将降低,因此在进行振动初始角的确定时,需对产能和洗净率综合考虑。
综合分析,各影响因素中,水射流系统相关因素对洗净率影响较大,针对与模拟颗粒相似的农产品颗粒清洗,清洗效果较佳的参数组合为:喷嘴入口压力为0.7 MPa,喷嘴方向角为π/3,振动槽振动频率为3 Hz(数值模拟结果较佳值是2 Hz,后经样机试验,较佳参数是3 Hz),振动初始角为π/5。
4 试验验证
根据上述理论研究结果,设计了相应的颗粒型农产品清洗试验台,试验清洗对象为带土干燥花生,如图11所示(实际生产过程中,清洗对象为刚出土的湿花生,并在清洗前进行筛分,去除大块土壤颗粒,本试验清洗对象为干燥花生,是因为干花生相对于刚出土的湿花生更难于清洗,试验结果的差异性将更显著。考虑到不同农产品颗粒表面尘土形状不一,数值模拟颗粒模型简化为球体,与实际颗粒略有差异)。

图11 待清洗的干燥花生 Fig.11 Dry peanuts to be cleaned
试验采用4组不同参数组合对带土花生进行清洗,参考中华人民共和国农业行业标准《蔬菜清洗机洗净度测试方法》中规定的洗净率计算方法,分别统计出经清洗机清洗且沥干后洗净的质量和未洗净的质量,再计算洗净率。试验后首先对清洗后的花生颗粒进行清洗效果评价,其中,清洗干净的颗粒必须为清洗后肉眼观察颗粒表面、夹缝内无泥沙及腐质等杂质。检验时观察每个花生单元的所有表面,颗粒表面有1处污渍面积小于1 mm2或有2处以上及5处以下污渍且污渍面积小于0.5 mm2的定义为洗净颗粒,否则为未洗净颗粒。为了提高试验可信度,每组试验分别进行3次独立试验,最后计算出平均洗净率,相关参数组合和洗净率如表4所示。
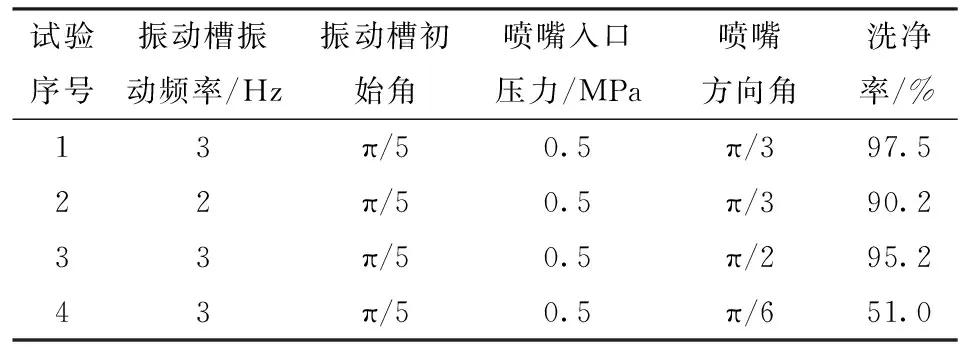
表4 试验参数与洗净率 Tab.4 Experimental parameters and cleaning rate
各组参数清洗效果如图12所示。试验结果较好地验证了理论分析结果。

图12 不同参数组合清洗效果 Fig.12 Cleaning results under different conditions
5 结论
(1)通过力学分析与FLUENT-EDEM固液耦合模拟相结合,对连续非淹没式水射流振动清洗颗粒型农产品进行研究,分析了振动槽振动频率、振动槽振动初始角、喷嘴入口压力和喷嘴方向角等因素对洗净率的敏感性,并进行了试验验证。
(2)在颗粒型农产品连续非淹没式水射流振动清洗过程中,喷嘴入口压力、喷嘴方向角对洗净率的敏感性最大,振动槽振动频率和振动初始角对洗净率的敏感性相对较小。同时发现,在清洗过程中,存在最佳的喷嘴方向角和振动槽振动频率,在清洗设备设计中,喷嘴方向角和振动槽振动频率可调,将有利于洗净率的提高。
(3)试验结果与理论分析结果具有较高的一致性。
