30m波形钢腹板箱梁桥设计与计算

钱玉宝，钱雪松，罗熙

（1.安徽省路港工程有限责任公司，安徽 合肥 230022；2.合肥工业大学，安徽 合肥 230022）

波形钢腹板组合箱梁桥是一种新型的组合梁桥，它使用波形钢腹板代替原来的混凝土腹板。相比混凝土腹板，它具有以下优点：①因为取代了混凝土腹板，且钢腹板的重量和厚度相较于混凝土腹板都要小，所以箱梁的自重得到减小，从而使恒载内力减小；②根据波形钢腹板的特点，它具有手风琴效应，这一效应会使预应力效率得到提升；③由于波形钢腹板组合箱梁桥省去了PC钢材配置、混凝土腹板钢筋、混凝土灌注等工序，使施工步骤得以简化；④波形钢腹板组合箱梁桥的出现，有效解决了传统预应力混凝土梁桥根部混凝土腹板开裂和跨中部持续下挠两大工程病害。

本文研究的是30m跨径的波形钢腹板组合箱梁桥的设计，采用midas软件进行桥梁建模设计，再利用模型，通过midas软件的分析功能对其进行力学性能分析，研究该模型桥梁的可行性。通过对这一桥梁的设计研究，使其对以后的研究工作起到技术支持作用，也对波形钢腹板组合箱梁桥在以后的应用和研究起到推动作用。

1 桥梁结构设计及参数确定

本文针对某30m波形钢腹板预应力混凝土箱形简支梁桥进行设计，桥梁计算跨径30m，桥面全宽12m（0.5m护栏+1.75m路肩+3.75m左车行道+3.75m右车行道+1.75m路肩+0.5m护栏=12m），桥梁横坡：1.5%，公路-II级，两车道，采用满堂支架法施工。主梁高度为1.75m；桥梁主梁两边翼缘宽度都为2.8m；主梁间隔每7.5m设置一块混凝土横隔板，横隔板厚度为20cm；桥梁主梁顶板厚度为22cm,底板厚度为25cm；箱梁腹板采用1000型波形钢腹板直腹板；采用体内体外相结合的预应力钢束布置形式，体内顶板3束、底板5束，体外束为5束，φ15.2Strand1860钢绞线；均为桥面铺装：上层采用8cm的沥青混凝土层，下层采用防水混凝土10cm。

桥梁采用的材料：主梁的上下顶底板采用C50混凝土；横隔板，横隔梁均采用C50混凝土；波形钢腹板采用Q345钢材（屈服应力345MPa；设计荷载作用下允许剪应力为120MPa）；预应力钢束采用φ15.2高强度低松弛钢绞线（抗拉强度标准值为fpk=1860MPa，正常允许拉应力ftk=1209MPa，抗拉强度设计值ftk=1260MPa）；防撞护栏不参与受力，采用C30混凝土。

桥梁横断面图和一般构造图如图1、图2。

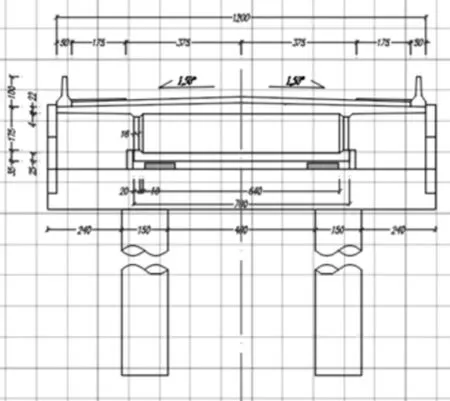
图1 桥梁横断面图

图2 桥梁上部结构平面图

2 数值建模

采用Midas软件对第一节中设计的桥梁进行数值建模，利用软件中自带的波形钢腹板箱型截面进行截面数据的输入。全桥共建立33个节点，形成32个单元，如图3所示，简支梁约束见图4。

图3 主梁斜截面视图

图4 边界条件示意图

桥梁荷载除了移动荷载（单独考虑），考虑了自重（包含节点荷载）、二期荷载、预应力和温度荷载。首先，在Midas中，定义静力荷载工况，分别添加自重（施工阶段荷载）、二期荷载（施工阶段荷载）、预应力（施工阶段荷载）和温度荷载（温度荷载定义不考虑温度梯度的影响，只采用系统温，采用整体升温20℃和降温20℃相结合的温度荷载）。

本桥梁采用满堂支架现浇施工，施工方法明确，支架一次整体落架，其中没有体系转换。施工方法可以分为3步：第一步为现浇PC组合箱梁（90d），激活结构组1、边界组1和2以及自重荷载组；第二步为锚固预应力钢束（30d），激活预应力荷载组；第三步为桥面铺装以及桥梁收缩徐变过程（3650d），激活二期荷载组和温度荷载组。

3 计算结果分析

3.1 支撑反力

①施工阶段：本桥梁采用了满堂支架施工方法，所以施工阶段的成桥阶段包括：加载自重，布设预应力钢束以及桥面铺装，加载二期恒载。所以，考虑自重、预应力和二期荷载桥梁的支座反力可以由Midas得到（反力只有竖向的），施工阶段结束之后，桥梁的支座反力Fz=1870.8kN。

②成桥阶段：成桥之后，根据规范《公路桥涵设计通用规范》（JTG D60-2015），基本组合为：1.2×箱梁自重+1.2×预应力+1.2×二期荷载+1.0×徐变+1.4×移动荷载+1.4×温度荷载，成桥之后的基本组合的支座反力Fz=3677.3kN。

3.2 内力组合

3.2.1 承载能力极限状态下的作用效应组合

作用基本组合的效应设计值可按式（1）或（2）计算：

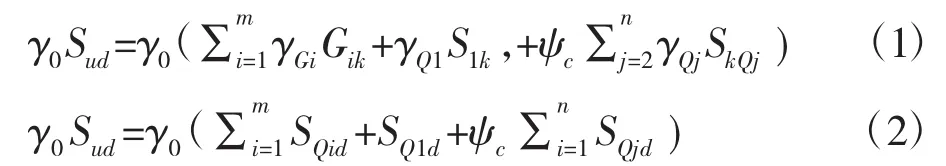
由上得知，基本组合为1.2×箱梁自重+1.2×预应力+1.2×二期荷载+1.0×徐变+1.4×移动荷载+1.4×温度荷载的效应组合。根据Midas可得，如图3.1所示，基本组合效应作用下产生的最大剪力位于右支座处，最大值为2722.5N。

图5 基本组合作用效应下的剪力包络图

3.2.2 正常使用极限状态下的作用效应组合

按正常使用极限状态设计时，根据不同的设计要求，采用两种作用效应组合分别是作用短期效应组合和作用长期效应组合。

①作用短期效应组合

永久作用标准值效应与可变作用频率值效应相组合，其效应组合表达式为：

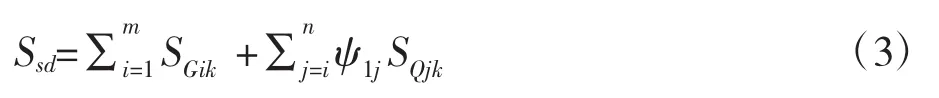
由Midas可得，作用短期效应组合产生的最大剪力产生在右支座处，最大值为1640.1kN。如图6所示。

图6 作用短期效应组合下的剪力包络图

②作用长期效应组合

永久作用标准值效应与可变作用准永久值效应相组合，其效应组合表达式为：

由Midas可得，作用标准效应组合产生的最大剪力在右支座处，最大值为1947.0kN。如图7所示。

图7 作用标准效应组合下的剪力包络图

3.3 应力验算

3.3.1 施工阶段的应力验算

由于波形钢腹板组合箱梁桥所承受的剪力近似由波形钢腹板承担，所以只进行正截面应力验算。通过Midas,下面对施工阶段结束之后的应力进行验算，如图8、图9所示。

图8 施工阶段结束后主梁上缘位置1的正应力图

图9 施工阶段结束后主梁下缘位置4的正应力图

在施工阶段结束之后，主梁截面上缘处全面受压，最大压应力出现在左右支座位置，最大值为5.82MPa，满足公路桥规的要求：5.82≤0.70fck=0.70×32.4=22.68MPa。

在主梁截面下缘处未出现拉应力，截面全面受压，最大压应力出现在支座位置，最大值为3.66MPa，满足公路桥规的要求：3.66≤0.70fck=0.70×32.4=22.68MPa。

3.3.2 使用阶段的应力验算

在《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2012）中，第7.1.1条要求，在使用阶段，应采用标准组合计算，即：1.0×自重+1.0×预应力+1.0×二期荷载+1.0×温度荷载+1.0×移动荷载+1.0×徐变+1.0×收缩。由Midas可以得到标准组合的应力图，如图 10、图 11。

图10 标准组合下的上缘处应力图

图11 标准组合下的下缘处应力图

在桥梁使用阶段，标准组合作用下主梁截面处全面受压，最大压应力出现在跨中处，最大值为7.51MPa,满足公路桥规的要求：7.51≤0.60fck=0.60×32.4=19.44MPa。

在主梁截面处未出现拉应力，截面全面受压，最大压应力出现在支座处，最大压应力为3.50MPa，最小压应力出现在跨中，其值为0.45MPa。满足公路桥规的要求：3.50≤0.60fck=0.60×32.4=19.44MPa。

3.3.3 正截面抗裂验算

①作用效应短期组合

根据《公路桥涵设计通用规范》(JTG D60-2004)，采用作用效应短期组合进行计算，即：1.0×自重+1.0×预应力+1.0×二期荷载+1.0×徐变+1.0×收缩+1.0×移动荷载+0.8×温度荷载。由Midas可以得到在作用效短期组合下的应力图，如图12、图13所示。

图12 作用效应短期组合下的上缘1点处的应力图

图13 作用效应短期组合下的下缘4点处的应力图

在作用效应短期组合下，主梁截面处全面受压，最大压应力出现在跨中处，最大值为6.95MPa，满足公 路 桥 规 的 要 求 ：6.95≤0.70fck=0.70×32.4=22.68MPa。

在主梁截面处未出现拉应力，截面全面受压，最大压应力出现在支座处，最大值为3.50MPa,最小压应力出现在跨中处，其值为1.09MPa。满足公路桥规的要求：3.50≤0.70fck=0.7×32.4=22.68MPa。

②作用效应长期组合

根据《公路桥涵设计通用规范》(JTG D60-2004)，采用作用效应长期组合进行计算，即：1.0×自重+1.0×预应力+1.0×二期荷载+1.0×徐变+1.0×收缩+0.4×移动荷载+0.8×温度荷载。由Midas可以得到在作用效应长期组合下的应力图，如图14、图15所示。

图14 作用效应长期组合下的上缘1点处的应力图

图15 作用效应长期组合下的下缘4点处的应力图

在作用效应长期组合下，主梁截面全面受压，最大压应力出现在跨中处，最大值为6.38MPa，满足公路桥规的要求：6.38≤0.70fck=0.70×32.4=22.68MPa。

在主梁截面未出现拉应力，截面全面受压，最大压应力出现在支座处，最大值为3.50MPa,最小压应力出现在跨中处，最小压应力为2.26MPa。满足公路桥规的要求：3.50≤0.70fck=0.7×32.4=22.68MPa。

根据以上结果分析，该桥梁的正应力，正截面承载能力正截面抗裂验算都合格，所以满足规范标准，接下来需要进行的是抗剪承载力验算。

3.4 波形钢腹板抗剪承载力计算

3.4.1 腹板剪切屈曲稳点性验算

本桥梁采用的波形钢腹板是1000型，厚度是10mm。根据波形钢腹板组合箱梁的性质，其剪力主要由波形钢腹板承受，所以需要对腹板的抗剪强度进行抗剪验算。

①局部屈曲强度：波形钢腹板弹性局部屈曲强度可按式（5）计算。

计算得到：τcr,l=884.38MPa。

②整体屈曲强度：波形钢腹板弹性整体屈曲强度由式（6）计算。

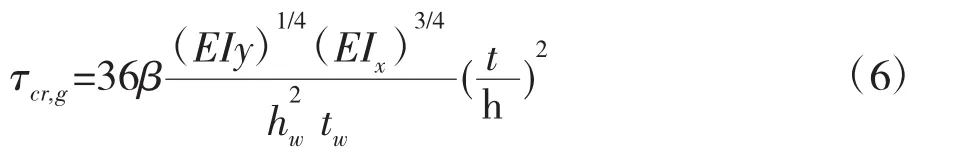
在荷载组合的最不利状态下，即上面得到的基本组合作用效应的最大剪力值，梁的最大剪力Q=2722.5kN。

每侧腹板所受的剪力：T=Q/2=1361.25kN。

计算得到：τcr,g=2355.14MPa。

③合成屈曲强度

波形钢腹板的合成屈曲强度由式（7）计算。

将每侧腹板所受的剪应力与局部屈曲强度、整体屈曲强度以及合成屈曲强度进行比较，得到每侧腹板所受的剪应力比它们的值都小很多，这就表明了剪力屈曲不会导致破坏。桥梁的抗剪承载力满足规范要求。

5 结论

本文针对30m波形钢腹板组合箱梁桥进行设计，利用Midas软件对桥梁进行建模，并且利用建立好的模型在Midas中进行力学性能分析，比如：剪力、弯矩、挠度以及应力；得到了桥梁模型的力学特性，并将其与规范相比较，确定设计桥梁模型的可行性；并对桥梁模型的截面正应力在不同施工阶段，作用效应下的验算，其结果均满足桥梁规范要求的；此外，还对桥梁的波形钢腹板抗剪承载力进行了验算，即计算桥梁的局部屈曲强度、整体屈曲强度以及组合屈曲强度，并将三者与桥梁在荷载组合最不利情况下的波形钢腹板所受的剪力进行比对，发现三者都远大于最不利剪力，满足规范要求。通过本次设计，证实了波形钢腹板组合箱梁桥相比于传统桥梁的优势，其刚度、施工效率、强度、抗震性等性质充分的得到了发挥，预计在不久的将来，波形钢腹板组合箱梁桥一定会得到广泛的应用。