一种基于改进的HHT短期风电功率预测方法*

宁康，廖晓辉

(郑州大学 电气工程学院, 郑州 450001)

0 引 言

随着风力发电在中国日益兴起，风电并网功率不断增加，兼之，风力发电随机、波动以及间歇性的变动特征，风电并网对电力系统要求的安全、可靠以及经济性的影响也日益显著[1]。因此，对于风电功率的预测，要求也更加精准。

因为风电的这些特点，文章挑选HHT(Hilbert-Huang Transform)作为主要的预测方法。HHT算法与傅里叶变换、小波变换等传统方法的优势之处在于：HHT算法不需要基函数，且自适应性强，不仅能够处理平稳信号，对于非平稳信号的处理也有着非常好的效果。HHT算法能够获得信号中各次分量的瞬时参数信息，可以完整地表现出信号随时间变化频率、能量分布的关系[2]。最初风电功率的短期预测，方法大部分基于较为单一的数据预测模型，例如卡尔曼滤波法、时间序列法、人工神经网络法、支持向量机、模糊逻辑法等[3]。近些年，究人员提出综合利用多种预测方法组合的方式，一定程度上提高了精度[4]。

文献[5]在考虑到风机尾流及环境等因素的基础上，将RBF子网和BP神经网络子网两种预测方法有效地结合在一起，从而对风电功率进行预测，此方法环境原因的限制较大。文献[6]利用CFD模型对于条件离散化的风电场来流进行预计算，以中尺度数值天气预报数据插值对风电功率进行预测。此方法对于数值天气预报数据本身的误差十分敏感，对于数据的依赖性较强。文献[7]在风电场四周建设测风点，由于不同方位风速具有关联性，对风电进行预测。可是在实际应用中，该方法投资额较大，不适合大范围推广。

文章采用一种基于HHT的组合预测法。该方法首先通过改进的镜像延拓方法对端点效应进行抑制，然后利用EMD(Empirical Mode Decomposition)分解数据。对得到的数据进行希尔伯特变换并分析样本中各个成分的特点，在此基础上分别搭建不同的预测模型。最后，对风电功率进行预测。文章使用该方法测试了河南某风场，结果证明该法对于风电功率短期预测有着良好的成效。

1 HHT理论

1.1 HHT原理

Hilbert-Huang是N.E.Huang等在1998年提出的对非平稳数据信号的处理有着特有优势的方法[8]。Hilbert-Huang变换可分释为经验模态分解、Hilbert变换两部分[9]。对于任意一个给定的复杂信号进行HHT变换，首先要满足两个条件：过零点、极值点的数量相当或相差1；原始信号极大、极小值决定的两条包络线均值为0。其EMD分解流程图如图1所示。

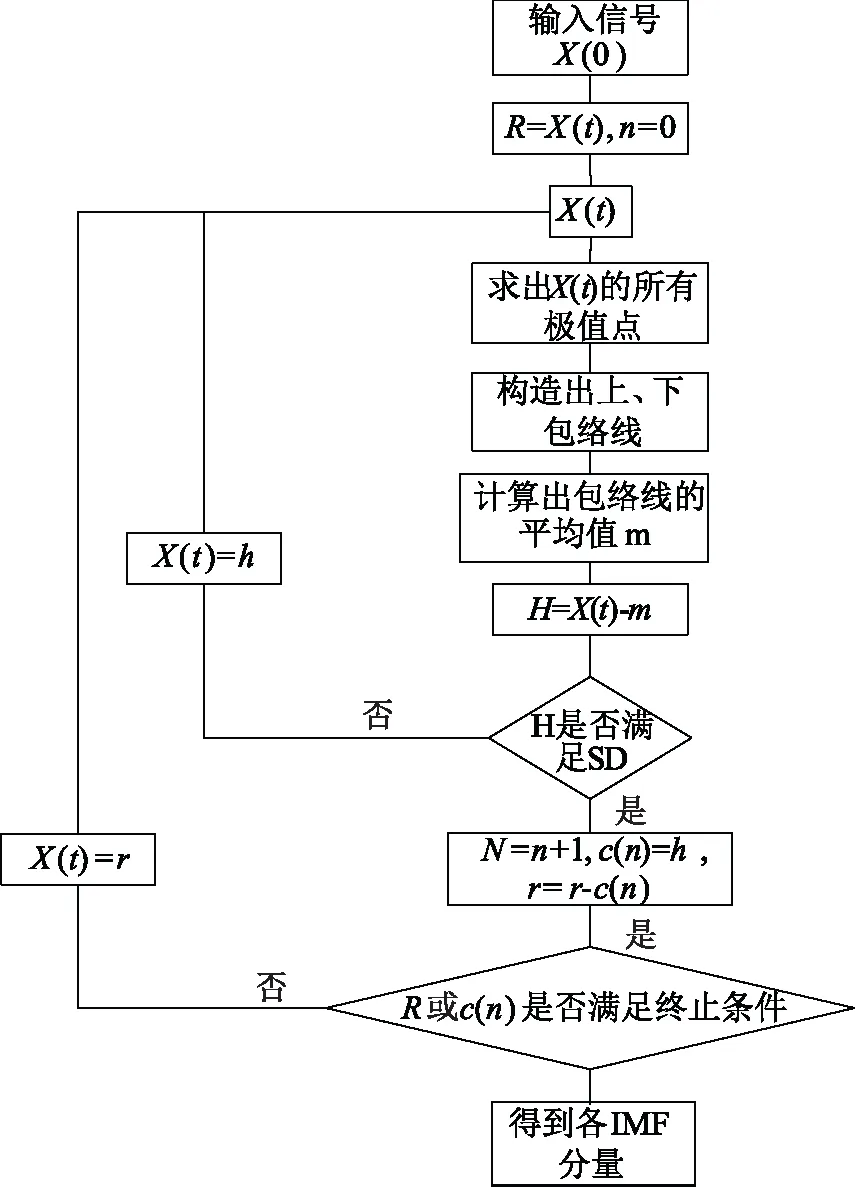
图1 EMD分解流程

EMD分解的终止条件：当cn(t)或rn(t)趋于单调，或小于终止值，分解过程结束。文章选用Gabriel Rilling提出的方法为经验模态结束的条件：

(1)

原始数据数据为IMF以及残余分量之和，即：

(2)

一个经过EMD分解的IMF数据进行Hilbert变换：

(3)

可以得出数据瞬时频率如下 ：

(4)

瞬时幅值如下：

(5)

相位函数如下：

(6)

用Hilbert变换所得出的数据，对于分析了解数据局部特征及变化规律，具有优异的效果。

1.2 端点效应问题

尽管在实际使用中HHT变换有其独特优势，可是因为端点效应影响而产生的问题却更加显著。

HHT的端点效应原因可以分为2部分: 第1部分，EMD在分解过程中[10]，要依据极大值、极小值点经过三次样条插值法取得信号包络线，并计算其平均值。包络线准确与否，关系到分解的完整程度。第2部分，对不完整取样的周期信号进行傅里叶变换求共轭，会出现频谱泄露，这种现象在信号两端出现，造成了Hilbert变换的端点效应[11]。

2 基于改进HHT的风电功率预测

2.1 基于BP神经网络的镜像对称延拓法

由于文章采用HHT的方法分析短时间内的风电功率历史数据，因此，在EMD分析中存在着端点效应问题。一般可以通过对信号两端添加一些数据点从而延拓数据，此时端点效应的影响就转移到了数据延拓后的两端，这样可以有效的对信号内的端点效应进行抑制。镜像对称延拓法时常用以处理分解中的端点效应问题。为了更好的抑制这个问题，采用一种基于BP神经网络改进的镜像对称延拓法。

对于BP(Back Propagation)神经网络，它模仿人类脑神经元，产生对外部刺激信号的反映，按照误差逆传播算法进行学习和训练的，其不须要领会表达映射关系的数学方程式，就可以训练并且储存大量的输入、输出以及映射关系，具有很强的自学习和自适应性[12]。文章选择基于此方法对端点效应进行改进。

2.2 组合预测

J.M. Bates[13]等提出了在经济科学领域的组合预测方法，通过一系列的模型进行复合预测，经过组合预测模型的结果，取加权平均值，以此改进预测效果[14]。组合预测是综合不一样的预测模型，提高准确度，增强可靠性，理论上是对各方法的最优求解。接下来，对文章采用的两种模型进行介绍。

时间序列是采样同距时间信息参数而取得的一组有序的数据，以过去时刻数值作为基石，用以推测将来某时刻值，文章选择AIC准则作为自回归模型。对于周期性较强的数据，该方法分析能力较好。

RBF(Radial Basis Function)亦是前馈型网络，其利用差值法，求取最佳逼近函数。RBF对单个输入参数，仅有少量的非零值，并且有着优秀的泛化能力，RBF神经网络具有局部逼近的性质。

2.3 预测步骤

文章提出的改进方法如下：

(1)归一化预处理原始数据；

(2)利用BP神经网络预测强而有效的数据容错性和泛化性，对已拥有的原始信号数据进行预测，即分别向左、右预测一定数量的数据；

(3)在此基础上，利用镜像对称延拓的方法对已加预测数据的信号进行延拓，经验模态分解已经经过镜像延拓的数据；

(4)在经验模态分解后，最终抛弃之上两端延拓的数据，截取中间部分，即与原始数据数量一致的经过模态分解的数据参数，作为最终的经验模态分解结果；

(5)进行希尔伯特黄变换，并分析不同特征的IMF分量；

(6)选择BP、RBF、时间序列方法处理不同特点模态分量，预测数据；

(7)综合上述各方法，取得最后的结果。

文章对不进行延拓的风电数据和进行延拓的数据进行了仿真对比，实验结果表明提出的镜像对称延拓方法具有很好的抑制效果。在BP神经网络向数据左、右端进行预测的过程中，过长或者过短的预测对于端点效应的影响不尽相同，选择适当的预测信号数量对端点效应有一定的影响。在风电功率预测的过程中，一般选择一天作为一个参数周期，所以文章选择24个点作为预测数对原始数据进行延拓。

2.4 评价指标

对于结果进行标准评价，是校验预测模型准确度卓有成效的方法。文章采用平均绝对百分误差，最大绝对误差，最小绝对误差三个不同的指标对预测结果进行客观评价。

平均绝对百分误差：

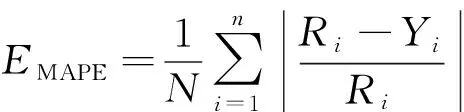
(7)

最大、最小绝对误差：

Eimax/min=Ri-Yi

(8)

3 仿真算例分析

文章使用河南某风电场4月的数据。通过对4月1日～4月29日功率数据进行建模，在已知数据的基础上再对未来三小时的的风电功率进行预测，滚动使用上述方法24次，最终取得未来三天的预测风电功率数据。

EMD分解已知风电功率数据，获得各模态分量波形图于图2。采用提出的改进镜像对称延拓来抑制EMD中的端点效应，在此基础上获得各IMF分量以及剩余分量波形图，如图3所示。

图中可以看到IMF2分量端点效应明显，而IMF3分量的端点效应有所好转。在图3的IMF2分量中，末端幅值激增受到一定的抑制，尽管出现了一定的端点效应，但其幅值范围已经基本稳定。IMF3分量在两头的端点效应显著弱于图2中对应的IMF分量,其幅值激增范围在一定程度有所下降。图3的IMF4分量相较图2相应的IMF4两端，分解效果更佳。

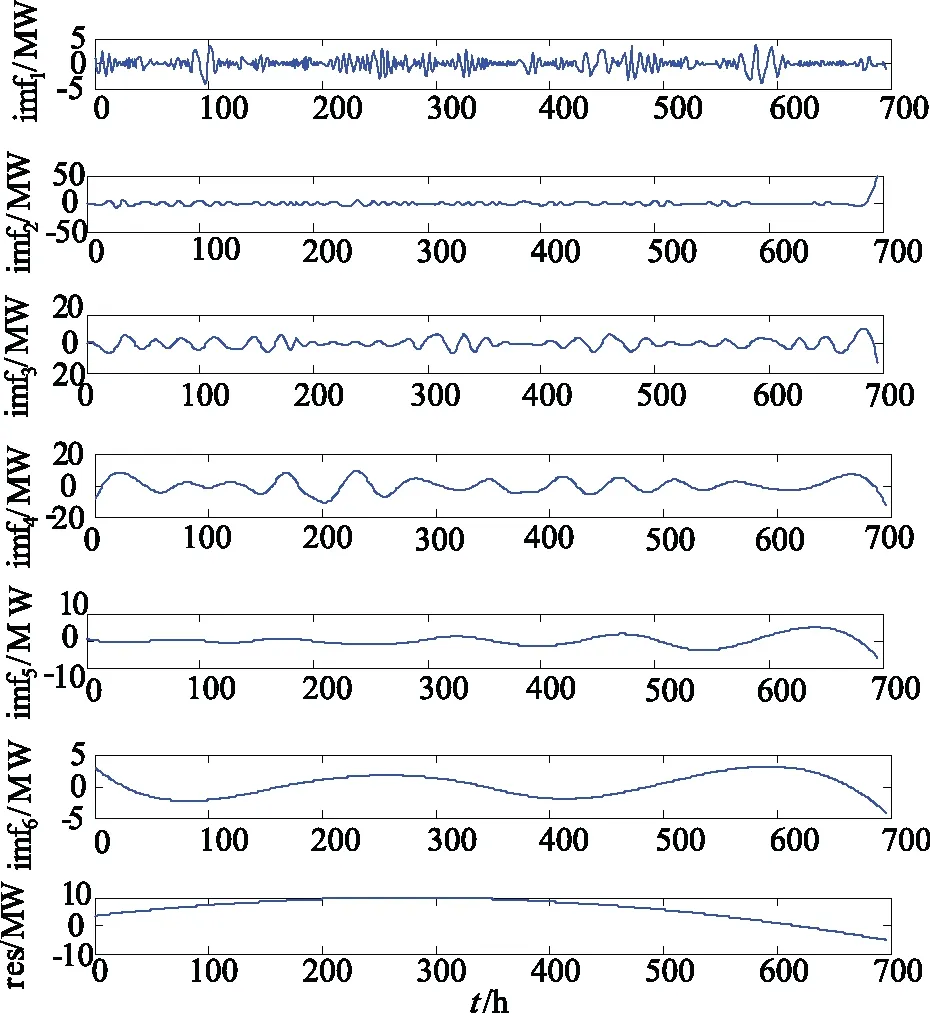
图2 直接对历史功率数据进行经验模态分解

图3 改进镜像对称延拓的经验模态分解

改进方法抑制端点效应，HHT进行变换后，IMF功率分量相应的瞬时频率如图4所示。

图4 六个分量对应的瞬时频率

为了直观了解模态分量的情况，算取每个IMF分量的瞬时频率的平均值。表1记录下六个模态分量的频率平均值。

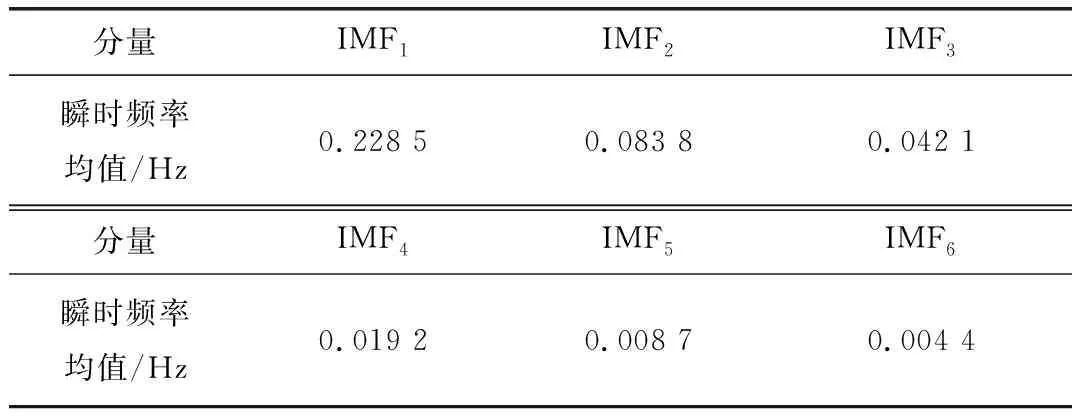
表1 六个IMF分量的平均瞬时频率

从表1可总结出，瞬时频率均值渐渐下降。EMD分解之后，通过分析各IMF不同的变化特征，最终比较选择RBF神经网络预测方法，对IMF1进行建模；以BP神经网络方法，对IMF2和IMF3进行预测；采用时间序列模型的方法预测其他模态分量以及剩余分量r。

依照模态分量的不同特征，采取不同的预测方法建模，取得其预测值，叠加几种预测方法取得的数据，最终得到风电功率预测数据。以此方法对未来3天(72小时、总计24次)滚动预测，即可得出未来3天，即72个风电功率预测值。

为了比较，分别单独采用BP神经网络、RBF神经网络两种模型，对原始数据建模，并将取得结果与文章提出方法结果比较于图5中。

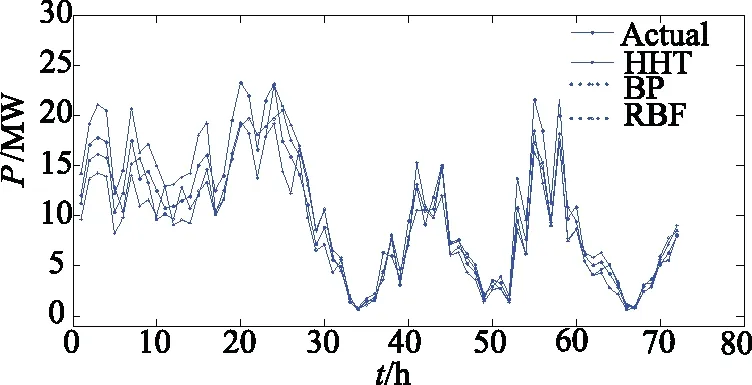
图5 模型预测结果对比

为了更好对比各预测模型结果，文章选取3个不同指标，描述各模型误差，如表2所示。

表2 评价指标结果

从表2得出，文章所采用组合模型方法比之两种单一方法更具优势。该方法数据结果较单一方法的最大、最小绝对误和平均绝对误差更小。

4 结束语

采用了一种基于BP神经网络的EMD分解方法，此方法在处理EMD端点效应的问题上具有一定的现实意义。该法以改进的模态分解法将河南某风电场功率数据加以分解处理，再使用希尔伯特变换，得到各IMF功率分量的瞬时频率，在此基础上分析数据并选择适合的预测模型，将预测结果组合叠加取得最终结果。通过与单一的BP神经网络、RBF神经网络相比，该方法具有更高的预测准确度。