单相电源法测量单回不对称线路阻抗参数的误差分析与改善措施

董清，邵鹏程

(华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引 言

随着电力系统规模的扩大，电网的结构日益复杂，线路走廊日趋紧张，为了节省线路走廊占地面积，减少线路建设成本，大多数的输电线路采用了不换位的架设方式，因此三相线路的参数会产生一定的不对称[1]，准确测量出每相线路的参数成为了研究的热点，线路参数对潮流计算、短路计算和继电保护整定有很大的影响，直接影响计算的准确性[2-5]，线路参数的准确测量与计算对电力系统的稳定运行具有积极的意义，新建高压输电线路在投运前[6-8]，除检查线路绝缘、核对相序、测量直流电阻外，还需要测量各种工频参数[9-14]，其中线路的三相阻抗参数[15]就是之一，目前现有的线路参数测量方法[16]，如异频法、工频法、扫频法和带电测量法，这些方法都是假定线路参数对称的情况下使用的，而对于单回不对称线路参数的测量方法很少，基于三相阻抗参数不对称的基本原理，目前提出了单相电源多变换接入方式的不对称输电线路参数分相解耦测量方法，这种方法的实质是一种单端测量[17]的方法，但是此种方法由于电流矩阵的求逆运算，在计算单回不换位线路三相阻抗参数时存在一定的误差，该文对此误差进行了定量的分析，并且提出了采用双端测量的方法在计算单回不换位线路三相阻抗参数时可以减小误差，由于测量电路当中考虑了大地电阻[18]对单回不换位线路三相阻抗参数计算的影响，该文提出了一种新的测量大地电阻的方法，这样能够更加准确的计算单回不换位线路三相阻抗的参数，最后以一条500 kV单回不换位线路验证了双端测量方法减小误差的可行性。

1 常规测量线路阻抗参数方法的误差分析

单回不换位线路三相阻抗参数分相解耦测量方法是通过在单相与地之间施加单相工频测试电源，线路末端三相短路然后与大地构成回路，在线路首端A相与地之间施加单相工频测试电源，同理，还可在B相与地之间、C相与地之间施加单相工频测试电源，根据测量得到的数据建立数学模型，得到一系列约束方程，将方程求解得到线路参数，测量电路图如图1所示。

图1 单回不对称线路参数测量电路

RA=RB=RC，XA≠XB≠XC

根据电路原理和测量数据，可以得到如下方程：

(1)

(2)

(3)

(4)

联立式(1)～式(3)，将测量结果写成矩阵形式，表达式如下：

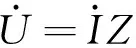
(5)

其中：

(6)

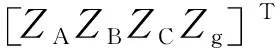
(7)

(8)

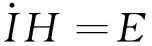
(9)

(10)

其中单位矩阵E表示如下：

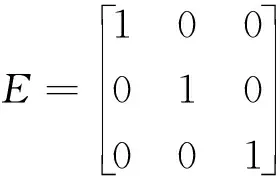
(11)

(12)

由式(12)可知，根据测量得到的电压、电流量可以求出各相阻抗参数和大地电阻的大小。当线路参数有很小的不对称性时，由于电流矩阵的求逆运算，最后会导致计算出的各相阻抗参数和大地电阻产生很大的误差，具体误差推导如下：

(13)

(14)

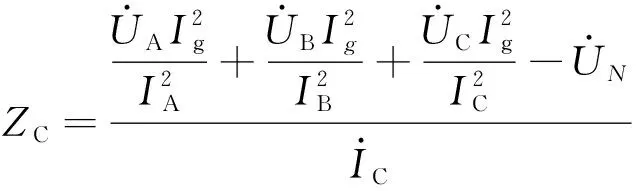
(15)

2 双端同步测量线路阻抗参数的方法

由于大地电阻的测量受到土壤电阻率、干扰信号等因素的影响，在测量当中会出现误差，因此本文提出了采用双端测量求大地电阻的方法，双端测量方法采用全球卫星定位系统可以测出线路首、末端电压和电流，测量的电路如图2所示。

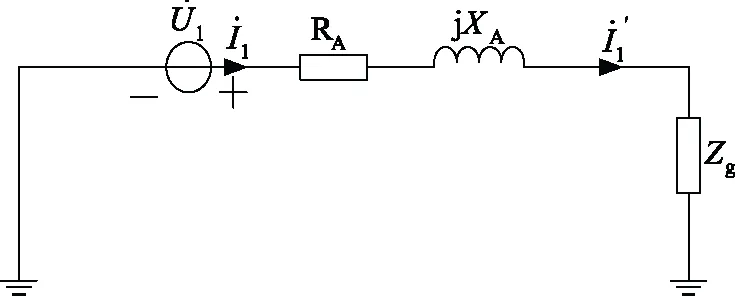
图2 大地电阻测量电路

图2的大地电阻测量电路当中，以A相线路为例，在线路首端施加单相工频测试电源，利用双端测量的方法可以测出首端的电压、电流和末端的电流，由KVL可得：

(16)

联立式(1)与式(16)可以求解得到大地电阻：

(17)

下面介绍利用双端测量求不对称三相阻抗参数的方法，由图1可知，对节点N列节点电压方程：

从而可得节点N的电压表达式：

(18)

利用双端测量方法可以测得大地电阻的大小，在图1当中三相不对称线路首端分别施加了单相工频电源，线路首端的电压、电流都可以测量得到，节点N的电压又可以表示如下:

(19)

(20)

(21)

(22)

3 单回不对称三相阻抗参数单端测量的误差分析

针对单回不对称三相阻抗参数的测量问题，在前文介绍了分相解耦测量方法，实际上是一种单端测量的方法，此方法是通过在单相与地之间施加单相工频测试电源，根据各相分别施加单相工频测试电源测到的线路首端电压、电流数据建立数学模型，得到一系列约束方程，将方程求解得到不对称三相阻抗参数和大地电阻的值，当单回输电线路的三相阻抗参数不对称时，电流矩阵的求逆运算会对参数的求解造成一定的误差，联立式(12)、式(20)～式(22)求得各相阻抗参数的误差大小分别如下：

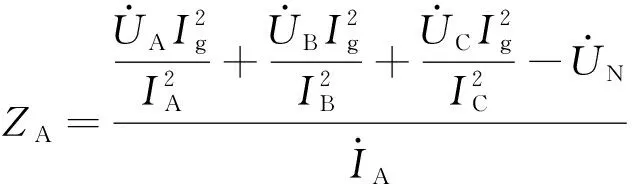
(23)

(24)

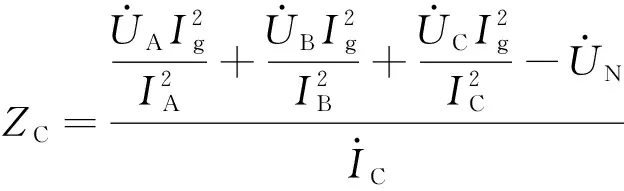
(25)

相对于双端测量方法计算单回不对称三相阻抗参数而言，ΔZA、ΔZB、ΔZC分别为采用分相解耦测量方法计算A、B、C三相阻抗所产生的误差，在实际测量中，为了减小测量误差，采用双端测量方法计算单回不对称三相阻抗参数更加准确。

4 单回不对称线路算例分析

由于高压线路不换位的现象日益增多，因此选取电压等级为500 kV的单回不对称线路进行计算分析，根据《电力系统设计手册》可知，选择500 kV架空输电线路的型号为4×LGJ-400/50，导线参数详见表1。

表1 4×LGJ-400/50导线参数

测量用的单回不对称输电线路的长度l=100 km，输电线路的各个参数的计算过程如下：

R=rl=0.018 08×100=1.808 Ω,X=Ll=

0.277 47×100=27.747 Ω

由于各相线路阻抗参数的关系如下：

RA=RB=RC，XA≠XB≠XC。

因此可令单回不对称线路各相阻抗参数如下：

RA=RB=RC=1.808 Ω，XA=27.747 Ω，

XB=30.5217 Ω，XC=33.296 4 Ω。

根据卡尔逊的推导[19]，大地电阻的公式可以表示为Zg=9.869×10-4f(Ω/km)，在工频50 Hz的情况下，Zg=0.05 Ω/km，因此当单回不对称输电线路的长度为100 km时，利用双端测量求大地电阻的方法可以令大地电阻的值Zg=5 Ω，A、B、C三相与地之间施加的单相工频电压大小分别如下：

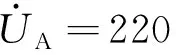
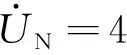
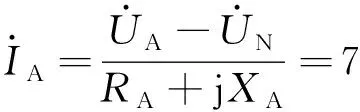
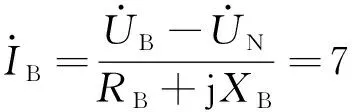
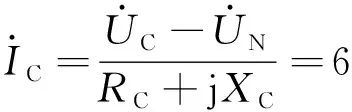
又由式(5)，联合式(10)，从而求得阻抗矩阵：

根据前面推导出的不对称三相阻抗的误差公式(23)～式(25)可得各相阻抗的误差：

ΔZA=(0.690 5+j0.133 5) Ω

ΔZB=(-0.534 5+j0.576 9) Ω

ΔZC=(-0.237-j0.779 1) Ω

根据分相解耦测量方法求得的大地电阻Zg=(-0.458 2-j1.001 5) Ω，对于100 km输电线路利用双端测量求大地电阻的方法把大地电阻的值取为5 Ω，由此可以看出采用分相解耦方法求单回不对称线路三相阻抗参数和大地电阻参数会产生很大的误差，从而对输电线路的运行计算产生很大的影响，因此采用双端测量的方法求大地电阻和三相阻抗参数更为准确，有利于输电线路的设计。

5 结束语

本文针对高压单回不对称线路阻抗参数的分相解耦测量方法进行了分析，并且针对此种方法计算阻抗参数和大地电阻产生误差的原因进行了分析，由于电流矩阵的求逆运算，在使用分相解耦方法求解阻抗参数和大地电阻时会产生很大的误差，经过分析得到了各相阻抗由于电流矩阵求逆产生误差的大小，为了减小误差，该文提出了双端测量的方法求解阻抗参数和大地电阻，最后以一条500 kV单回不对称线路为例，验证了使用双端测量的方法更能准确的测出实际的阻抗参数和大地电阻的大小，准确的测量线路参数对潮流计算和电力系统的安全稳定运行具有重要的意义。