基于图论矩阵的南水电厂配电网故障判定

,

(南水发电有限责任公司，广东 韶关 512600)

1 引言

配电网设备复杂，用户多，覆盖范围广，地理条件多样，因此需要使用更长的时间来判断故障点的位置。随着经济社会的发展和人们的物质文化生活水平的提高，对于电源质量和供电可靠性，用户的要求也越来越高，甚至不能承受瞬时中断的电力供应。在电力系统发电，变电，送电和配电的所有的环节中，对于用户电源的使用，配电网是最后一个环节。因此，全面实施配电网自动化是一项迫在眉睫的任务。在配电网发生事故的情况下，可以在配电网中尽快找到故障线段是配电网自动化的关键任务之一，即配电网的故障位置[1]。

目前，在配电网中实现故障定位的方法有两种。一种是基于分段器和重合器的配电网故障定[2-4]。当配电网发生故障，通过对重合器和分段器运行特性的记录和分析，然后设定时间和行动来确定故障的位置，数量，但故障位置的确定需要反复打开和关闭开关，这将导致励磁涌流，以及该方法要求大量的电力从配电网被提取，不利于电力供应的稳定。因此，基于分段式和离合器的配电网故障诊断方法不能满足电力系统发展的需要。另一种是基于馈线终端(FTU)配电网故障定位，主要分为两类：一类是基于人工智能算法的故障定位算法[5-6]。如专家系统算法和人工神经网络算法，模糊理论和遗传算法，然而，这种算法有很长的计算时间，在实践中，很难实现实时故障判断和处理的要求。另一类基于图论理论，通过分析配电网的拓扑结构，分析了故障的位置。典型的算法有一个矩阵算法，该算法简单直观，应用更多。

配电网故障的准确定位及快速隔离故障和恢复供电的措施是馈线自动化的重要功能之一。随着电网和配电自动化项目的广泛开展，大量的FTU在配电系统中的应用，为配电网络的馈线自动化功能的实现提供了保障。在这种情况下，文献[7]讨论了电气部件，例如部件，继电器和开关的动作序列之间的因果关系的故障位置。

文献[8-9]提出了一种用于故障定位的矩阵算法，解决了单电源中的环形配电网(开环运行)或径向配电网的故障定位问题，然而，该算法的缺陷在于没有一个统一的故障定位算法和矩阵，用于描述分布网络运行逻辑矩阵和故障信息矩阵，包括该算法中每个检测点的整个系统的所有位置信息，，使算法占用更多的存储空间，计算复杂度和计算时间。文献[10]提出了基于现场监测终端的解决复杂配电网故障定位问题而建立一个统一的故障定位算法，如在双电源、多电源并联供电系统中，提高定位算法的效率，但其定位结果受局部结构和故障位置影响。

考虑到上述算法的缺点，本文提出了一种基于图论的矩阵配电网故障定位算法的改进方法。该算法假定多电源馈线的正方向，简化了矩阵的生成条件和方法，并增加了位置矩阵的稀疏性，同时避免了复杂的矩阵乘法，降低了计算的复杂性，从而降低了矩阵的计算复杂度，节省计算时间。该算法还可用于确定多电源节点故障，故障终端等，并且可以实现快速故障定位，也适用于在缺省条件下对具有不完整故障信息的配电网故障进行定位。最后，故障定位测试在南水电站的工厂配电网中进行。南水水电站位于广东省乳源瑶族自治县东坪镇(原龙南镇)鸡公岐附近的南水河，是一座原以发电为主，结合改善防洪和灌溉等综合利用的枢纽工程，南水电厂厂区配电网由3个电源供电，分别是南水主机组，南源小机组为备用厂区电源，以及从市电接线引入厂区供电。

2 基于图论的网络拓扑描述

2.1 图论相关定义

定义1 由有限个不同顶点与连接其中某些顶点的边组成的图形称之为图。

一般可将图表示为G=(V，E)，V是其所有顶点的集合，V=[v1,v2,…,vn]；E是其所有边的集合，E=[e1,e2,…,en]。 在图论中，将点称作顶点，边是顶点的有序偶对。假设两个顶点之间当且仅当由一条边连接,则称这两个顶点具有相邻关系。

定义2 设G=(V,E)为一无重边的有向网，其中V=[v1,v2,…,vn]，那么NxN矩阵D=[dy]称为G图的邻接矩阵，记为D[G]。显然，邻接矩阵是表示顶点之间相邻关系的矩阵。其中

(1)

定义3 若a∈V及b∈V，则当且仅当aHb时，才有(a,b)∈V。若aHb等价于bHa，即(a,b)=(b，a)，则G=(V,E)是个无向图。反之G=(V,E)是个有向图。

显然，上述定义是指如果图G中的各条边具有方向性称之为有向图，反之则为无向图。

2.2 图论与配电网的逻辑关系

对配电网结构进行分析，不难发现：配电网结构通常有三个，即树状网络、散射状网络和开环运行状态的环网。但无论是什么样的网络结构，它由配电馈线，开关和配电变压器组成。因此，基于上述图论定义，可以简化配电网的组成，并且可以满足配电网拓扑的图论定义。

依据定义1，可以把开关看作是配电网的一个顶点，配电线路和配电变压器和其他综合看做边，然后将配电网抽象为一个数学逻辑图，因此图的定义是用来描述开关在配电网中与配电馈线的链接关系。然后，配电网的拓扑结构可以通过定义2的邻接矩阵来描述。

2.3 配电网的有向图拓扑描述

考虑到配电馈线的电流方向，而这个方向也是电路的电流方向，由定义3可以看作是一个有方向的边。如果在配电网络中有N个节点，则可以通过N阶邻接矩阵D来描述配电网络(以下称为网络拓扑矩阵)。如果在节点i和j之间只存在一条边(假设由i指向j)，矩阵D中元素dy=1，其余情况下矩阵中的其他元素和末端节点均为0。

有向图的拓扑矩阵D描述了当前配电网的实际运行情况。在单电源供电网络的供电模式下，馈线的正方向是电源线的功率流出方向；在多电网供电模式中，首先必须假定电源，且只由一个电源供电，电源到配电网络的功率流出方向是馈线的方向。以南水电厂配电网举例说明，可将南水电厂的配电网假设为3电源供电、8节点的FTU故障监测终端。

在图1中，节点1～8为柱上开关，每个节点处配备有FTU，W1，W2，W3为供电电源(南水电厂发电机、南源电厂发电机、市电电源)。如果W1假定为供电电源(也可以认为是W2和W3)，则该电源的功率流出方向是馈线的正方向(如图1中的箭头)。在实际应用中，选择电源线最短的电源作为假定电源。由图1可得：d12=d15=d23=d24=d56=d58=d67=1，其他元素都是0，生成8维网络拓扑矩阵。

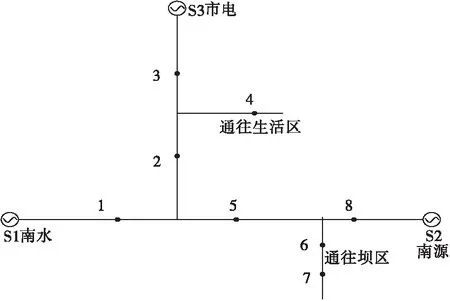
图1 南水电厂配电网拓扑

(2)

使用由该算法生成的网络拓扑矩阵，忽略反向连接中的-1元素，因此，当逻辑元素被确定时，矩阵生成更快；同时，由于只有0，1的两个元素，可以生成更好的稀疏矩阵，随后的矩阵运算速度会更快。

3 改进矩阵定位算法

本文提出了基于图论理论的故障定位算法。首先，根据配电网本身的物理结构(有向拓扑结构)，可以生成网络拓扑矩阵D，该矩阵包含了配电网络的拓扑信息。然后，当配电网发生故障，FTU上传故障信息到配电主站产生故障信息矩阵T；接着网络拓扑矩阵D和故障信息矩阵T作算术加法运算，获得故障判断矩阵Z;最后根据具体的故障定位判断条件对矩阵Z进行逐一判定，判断配电网发生故障的区间。

3.1 故障判断与故障检测

运行班组的监控中心可以实时监控总线电压，并确定配电网络是否有故障。当发生故障时，安装在每个开关处的FTU将收集并发送故障电流信息到监控中心。根据故障前后故障电流波动的特点，监控中心生成相应的故障信息矩阵T。目前我国配电网主要采用小电流接地形式，在发生单相接地故障时，故障电流瞬态分量具有较大的幅值，不受电弧抑制线圈补偿影响特性的影响。单相接地故障检测的特点是在配电网中出现相位故障时，附加阻抗零序阻抗效应减小，T频降低，产生较大故障电流，其幅值大，可不考虑负载电流的影响。据此可检测相间故障。

3.2 故障判定矩阵的生成

故障信息矩阵T是一个对角矩阵，对角线上的元素的值的含义表示每个开关是否发生故障。假设第i个开关发生了故障，并且开关的故障电流方向与配电网中的馈线的故障电流方向相同，则第i行第i列元素为“1”，即fii=1，否则为“0”。仍然以图1中南电厂的配电网为例，如果在配电网中节点6和7之间，节点8末端发生故障(图2)，则故障电流流过节点1，5，6，8，即有f11=1，f55=1，f66=1，f88=1，得到故障信息矩阵T。最后，故障判断矩阵Z是通过D+F相加所得。

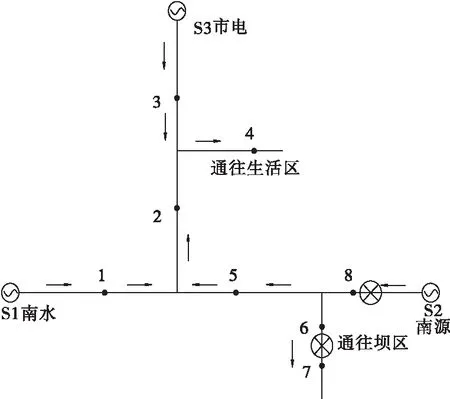
图2 多电源配电网络故障模型

T=diag[10001101]

(3)

(4)

相比文献[11-15]，当形成故障信息矩阵并形成故障判断矩阵时，可以以两种方式改进该算法：

(1)将配电网的网络拓扑矩阵和故障信息矩阵直接相加，以避免由矩阵乘法导致的计算复杂度过大，而且更加简洁快捷；

(2)该算法生成的故障信息矩阵是一个只有0和1个元素的高度稀疏矩阵，它可以大大降低计算成本，提高了计算效率，忽略了反向故障电流的-1存储。同时，配电网节点的故障值是相反的，使故障信息更直观。

3.3 配电网故障区段判据

(1)配电网节点末梢馈线段故障。若故障判定矩阵Z中元素满足：Zii=1，且对j(j≠i)均有Zij=0，即i行除列j外均为0，则判定节点i末梢馈线段有故障。由式(4)可得：Z88=1，而第8行其他元素为0，进而判定8节点末端馈线段发生故障。

(2)配电网节点之间的馈线段故障。若故障判定矩阵Z中元素满足：Zii=1且对Zij=1时都有Zjj=1，其中j(j≠i)，则判定节点i和j之间为馈线故障区间。由式(4)可得：Z66=1，Z67=1，Z77=1，由此判定故障发生在节点6和7之间。

采用该算法的判定原理清晰，避免了随着配电网中的用电节点或电源数量的增加，造成故障判定算法计算繁琐，实用性变差的缺点。

4 不完备故障信息的定位方案

在实践中，由于对安装在室外的栏目更多的配网开关，在外部环境因素(包括温度变化的同时，雷电电磁干扰等)对配电网的影响下，可能会导致辅助开关触点接触而导致失败或误报，即FTU采集到错误故障信息和报告错误故障信息。FTU故障信息报告不完整，这将严重影响电厂员工的对配电网故障的定位、隔离和恢复配电网网络。因此，为了保证配电网的可靠性，配电网的故障定位必须是准确可靠的，因此其故障定位算法也应具有较高的系统容错能力。

针对上述问题，该算法采用了对不完全故障信息的节点删除的方法。当节点i故障信息丢失时，生成相应的网络拓扑矩阵和配电网故障信息矩阵，该算法不考虑此节点，但故障判断矩阵的最终形式仍然可以使用故障判据原则来确定故障区域或位置。

仍以图1为例，若配电网上的6、7节点之间发生故障，而节点6故障信息缺失，则形成网络拓扑矩阵和故障信息矩阵分别为

(5)

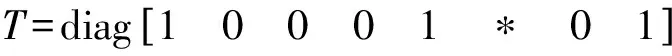
(6)

由D+T可得故障判断矩阵Z，

(7)

根据前述内部节点失效判据的方法可以确定节点，节点在5和7之间的配电网络之间发生故障，故故障区段确定，虽然一些故障区段有所扩大，但故障点而不会因为不完整的故障信息系统被覆盖，导致信息丢失或判断错误。

5 算例测试与比较

与其他算法相比，可以解释该故障定位算法简单有效。此方法还使用了无向图的逻辑抽象的配电网络的拓扑结构，基于网络拓扑和故障信息矩阵矩阵乘法，网络拓扑矩阵和故障信息矩阵相乘和归一化后，异或运算是用来判断故障区间。假设在图2中配电网馈线故障模式相同，并且馈线的正方向仍然是被提供为电源S1的功率流出方向，网络拓扑矩阵D是对称的。

(8)

故障信息矩阵T取值与本文方向相反，如果节点i检测出有故障，则fii=0，否则为1；

T=diag[01110010]

(9)

将D与T矩阵相乘，得到预制矩阵Q，

(10)

对Q进行规格化处理，具体流程不再赘述。由式(8)和式(9)可得：f22=1，d12=d32=d42=d52=1，f11=f55=0，故将Q的第2行和第2列的元素全部置换为0，得到故障判断矩阵P。

(11)

由式(11)可得，p67⊕p76=1，可判断配电网上的节点6、7之间存在故障，但无法该算法判断节点8末梢有故障。

由于本算法生成的故障信息矩阵为8阶的对角矩阵，通过该算法需要8×8 =64逻辑运算和一系列的规范化操作得到的决策矩阵。在本文中，该方法只需要修改D矩阵的对角元素，只有8个基本的逻辑或操作即可，而且还可以正确地确定终端故障。图2为程序设计实例，故障诊断程序流程图如图3所示，故障定位程序的实例，用于测试结果如表1所示。

表1 算例测试对比结果

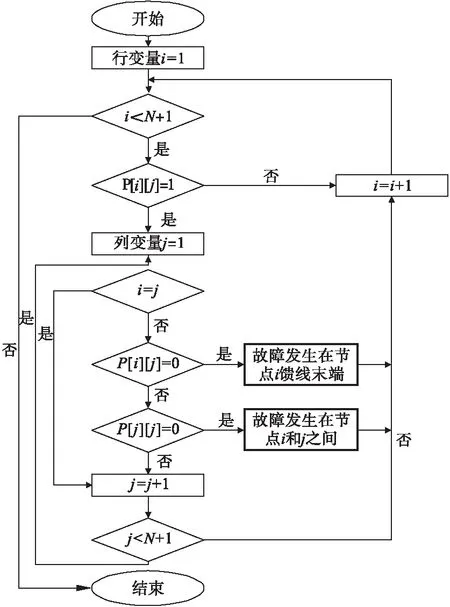
图3 故障判定程序算法

5 结语

本文提出了一种改进的基于图论的矩阵故障定位算法。在生成网络拓扑矩阵的配电网故障信息矩阵，算法假定多电源网络条件下的配电网馈线的正方向，同时忽略以往算法中由于反向电流造成的-1元素，只有0和1元素，提高位置矩阵的稀疏性，避免矩阵复乘，降低了计算复杂度，从而降低了矩阵的计算复杂度，节省了计算时间。

此算法不仅能够用于终端发生故障及故障定位的条件下的快速检测和定位节点的配电网故障，而且由于FTU故障导致配电网故障的问题从而产生不完整的故障信息也是适合的。以粤电集团南水发电厂为例，测试结果表明故障定位算法简单实用，通过直观的判断，大大缩短了故障判断的时长，也可以实现配电网故障区域的快速定位，方便维修人员进行维修抢修。