基于内点法的最优潮流计算及算例分析
2018-08-30,
,
(广西大学电气工程学院,广西 南宁 530004)
1 引言
最优化方法形成的历史较短,它主要采用数学手段提出各种系统的优化途径及方案,为电力系统运行提供科学决策的依据。最优潮流问题要求算法具有收敛速度快的同时还要求算法简介,计算量少,以便其应用计算机求解。其求解常用的方法有:线性规划法、二次规划法、梯度及牛顿类算法、内点法和智能方法等[1]。
2 最优潮流模型及内点法
2.1 最优潮流模型
最优潮流模型的假设有:
(1)投入运行的火电机组的数量和运行情况已知。
(2)水电机组的出力已定。
(3)已知电网结构并且无变动。
数学意义上,最优潮流就是在一定约束条件下寻求最优状况的问题。其中主要包含各种变量、约束条件和目标函数。现在对已上三个方面做简单的介绍。
常见的模型中,变量主要分为两大类。一类是控制变量;另一类是状态变量。
最优潮流考虑的系统约束条件有:
(1)各节点功率平衡约束(细分为有功和无功两种)。
(2)各有功电源有功出力上下界约束。
(3)各无功电源无功出力上下界约束。
(4)系统中所能提供无功功率约束。
(5)移相器抽头位置约束。
(6)可调变压器抽头位置约束。
(7)各节点电压幅值上下界约束。
(8)各支路传输功率约束。
其中(1)约束为等式约束,其余约束为不等式约束。
最优潮流的目标函数根据实际情况不同有很多,最常用通常为以下两种:
(1)系统运行成本最小。该目标函数一般表示为火电厂煤耗量最少,即费用最低。由于其他成本变动不大,所以不考虑发电机组启动、停机和维护等费用,即认为发电成本为煤耗成本。其中发电厂的成本耗费特性是求解最优问题的关键,它决定了最终求解是否最优,还影响求解过程所用方法和最优模型的建立。其耗量特性通常用一个阶数少于3的多项式表示。若不满足该条件,目标函数将呈现非凸性,造成OPF收敛困难[2]。
(2)有功功率损耗最小。
实际调度运行中模型的目标函数主要是满足系统耗量最小,即耗费最低。其函数如下:
目标函数:
(1)
式中PGi表示系统中发电机的有功功率;a0i、a1i、a2i为其耗量特性曲线参数。
约束条件:
(i∈SB)
(2)
(3)
(4)
(5)
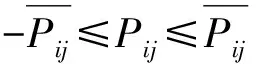
(6)
以上函数中式(2)为等式约束,即节点功率平衡方程;式(3)~(6)为不等式约束,依次为有功功率约束条件,无功功率约束条件,节点电压约束条件,复功率约束条件。在所建立模型之中用极坐标来表示节点电压。
2.2 最优潮流问题的内点法
最初,内点法的思路是通过在可行域内反复迭代最终得到最优解。因此,应在可行域内取目标变量的初值。并在求解过程中目标变量接近设定的边界时与之对应的目标函数会迅速增加,由此得到的解均在设定的边界以内[3]。可是在规模较大实际问题中,难以找到符合条件的初始点。本模型中使用跟踪中心轨迹内点法,其优势在与迭代计算中松弛变量和拉格朗日乘子满足不等式约束条件(通常与零比较)即可,简化了模型迭代过程。
为了便于分析,可做如下假设:把 [(1)~(6)]简化为一般非线性函数:
obj. min.f(x)
(7)
s.t.h(x)=0
(8)
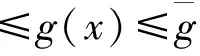
(9)
其中:式(7)为目标函数,对应于普通模型中式(1),为非线性函数。式(8)对应于普通模型中式(2),是非线性的;式(9)中的不等式约束也是非线性函数。在该模型中采用的基本思路如下。
首先,将不等式转化为等式约束:
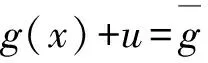
(10)

(11)
其中松弛变量l=[l1,…,lr]T,u=[u1,…,ur]T,应满足
u>0,l>0
(12)
这样,原问题变为优化问题A:
obj. min.f(x)
s.t.h(x)=0


u>0,l>0
由此,所求函数经过变换后,可以满足可行域范围内与原函数f(x)接近,而在接近边缘时则差异很大。因此可得到优化问题B:
s.t.h(x)=0

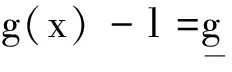
其中扰动因子(或称障碍常数)μ>0。
变换之后的拉格朗日函数为:
(13)
式中:y=[y1,…,ym],z=[z1,…,zr],w=[w1,…,wr]为拉格朗日乘子。目标函数存在极小值的必要条件是拉格朗日函数对所有变量及乘子的偏导数为0[4]:
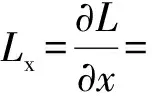
(14)
(15)
(16)
(17)
(18)
(19)
式中:L=diag(l1,…,lr),U=diag(u1,…,ur),Z=diag(z1,…,zr),W=diag(w1,…,wr)。由式(18)和式(19)可以解得:
定义
Gap=lTz-uTw
(20)
可得
(21)
式中:Gap称为对偶间隙。但是,上式中参数μ所取值会导致计算过程中收敛效果较差。实际中采用
(22)
式中:σ∈(0,1))称为中心参数。为取得较好收敛特性,通常取0.1。由于μ>0,u>0,l>0,由式(18)和式(19)可知道z>0,w<0。
对[(14)~(19)]线性化后得到修正方程组为:
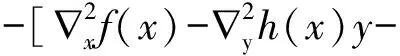
(23)
(24)
(25)
(26)
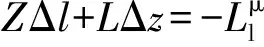
(27)
(28)
写成矩阵形式
(29)
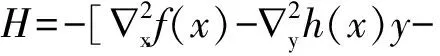
由于其系数矩阵是个(4r+m+n)×(4r+m+n)的方阵,因此迭代过程将变的非常复杂。需对其进行适当的简化:
(30)
现在,我们只需对一个相对较小的(m+n)×(m+n)对称矩阵进行LDLT分解,在求出结果后回代即可。这样,不仅减少计算量,同时简化了算法[5]。
方程(30)可以求解出第次迭代的修正量,由此可求出下次计算的新变量:
x(k+1)=x(k)+αpΔx
(31)
l(k+1)=l(k)+αpΔl
(32)
u(k+1)=u(k)+αpΔu
(33)
y(k+1)=y(k)+αdΔy
(34)
z(k+1)=z(k)+αdΔz
(35)
w(k+1)=w(k)+αdΔw
(36)
式中:αp和αd为步长。
程序算例的流程图如图1所示。其中初始化部分包括:
(1)设置松弛变量l、u,保证[l,u]T>0。
(2)设置拉格朗日乘子z、w、y,保证[z>0,w<0,y≠0]T。
(3)设优化问题各变量的初值。
(4)设置中心参数σ∈(0,1),并设置计算精度ε=10-6,迭代次数初值是k=0,最大迭代次数kmax=50。
3 算例计算
本文中采用内点法对9节点系统进行最优潮流计算,9节点系统具体参数数据见表1~表3。
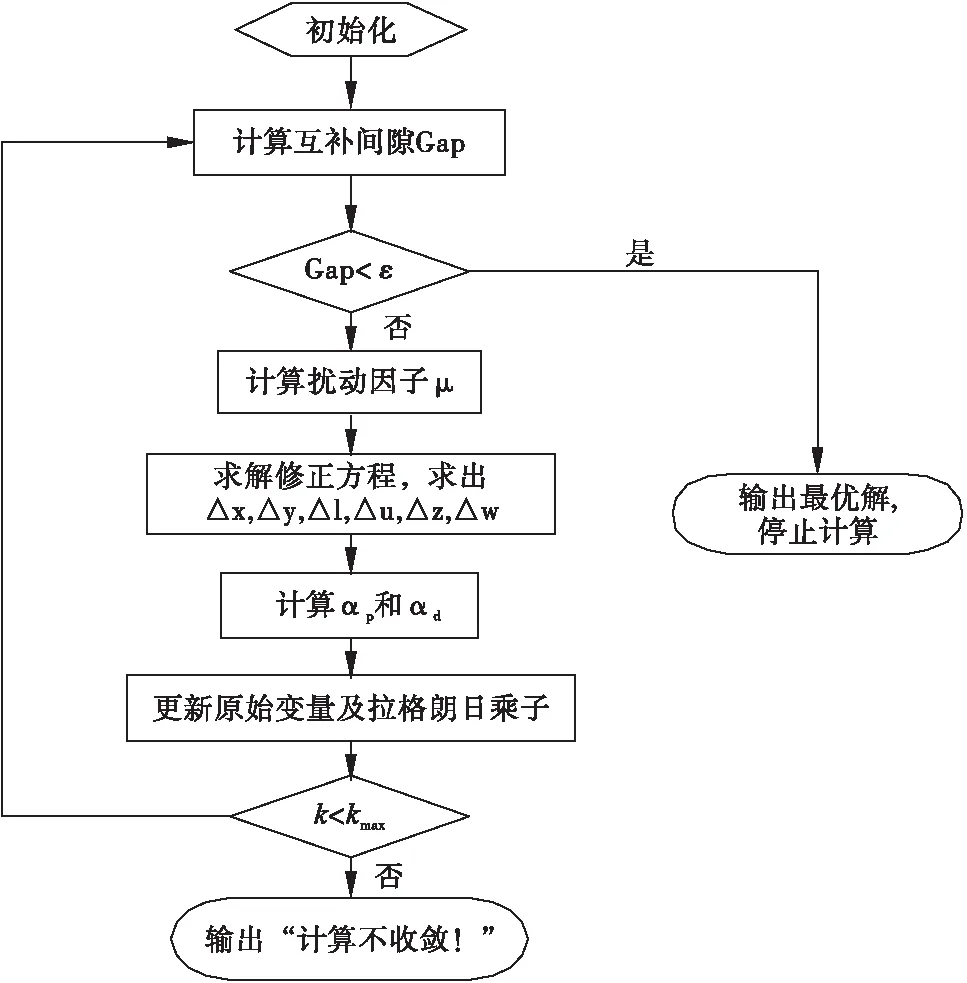
图1 基于内点法的潮流算法流程图。
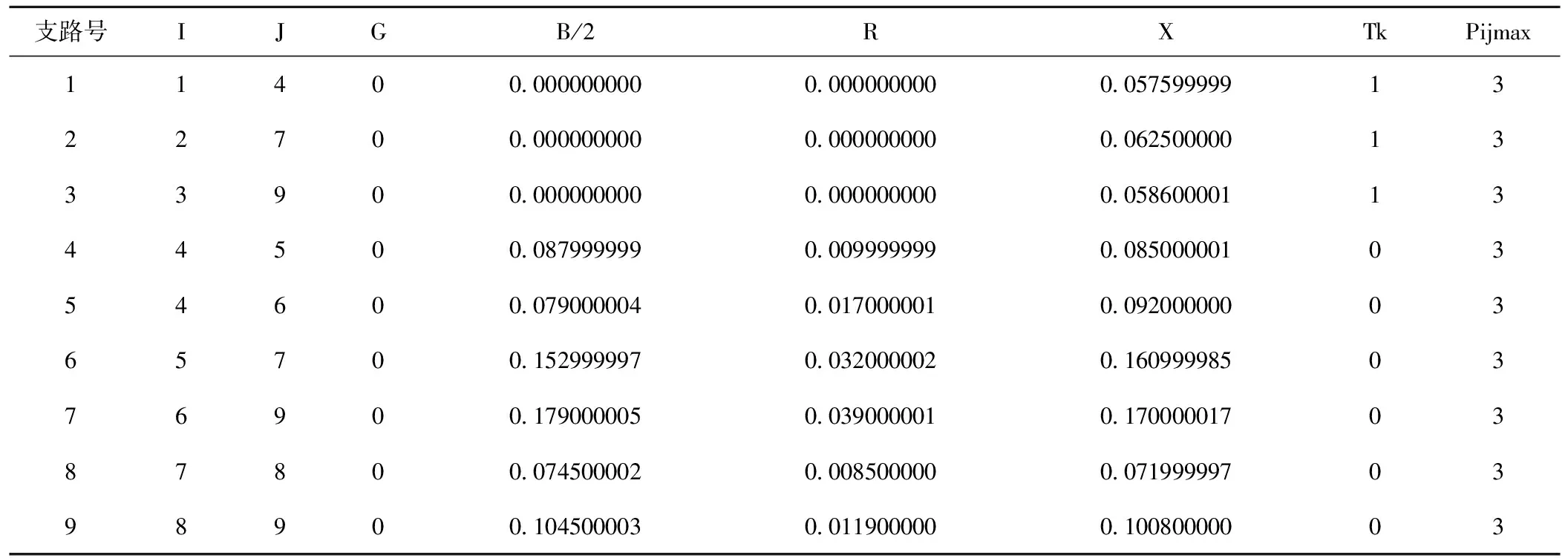
表1 9节点系统支路数据

表2 9节点系统发电机数据

表3 9节点系统负荷数据
在初始化时,各变量初值可以根据不同情况而设置。本计算中,各节点电压初值均为1,相角初值均取0,电压上界取1.06,电压下界取0.94[6];松弛变量,li=1,ui=1;拉格朗日乘子zi=1,wi=-0.5。按图1所示的模型计算,当程序收敛时,需要进行12次迭代。计算结果如下:

表4 发电机出力
计算所得整个系统的燃料费用为5303.629。

表5 各节点电压相量

表6 支路有功功率
4 结语
通过计算可以发现,采用内点法进行的寻优求解有效的简化了计算过程,减少迭代次数,提高实践应用的效率。
本文对最优潮流的内点法求解进行了深入的研究,构建了考虑稳定约束的最优潮流模型,并详细推导了其内点法求解过程。通过算例分析经行验证,有效简化了最优潮流的计算过程。
