NLOS环境中的拉格朗日乘子改进约束最小二乘定位算法*

李溯南,华惊宇*,王东明,周 凯,陈芳妮,余旭涛

(1.浙江工业大学通信网技术应用研究重点实验室,杭州 310023;2.东南大学移动通信国家重点实验室,南京 210096)

在无线传感器网络以及物联网领域,无线定位技术与基于位置的服务比如车载移动通信服务已经受到了广泛的关注。实际的无线传感器网络包括至少3个固定节点SN(Static Node)以及若干移动节点MN(Mobile Node),其中固定节点的位置信息已知而移动节点的位置需要根据得到的测量信息进行估计[1]。传统的定位算法通常采用一个或几个定位参量,根据算法采用的定位参量可以将算法分类为到达时间(TOA)[2]、到达时间差(TDOA)[3-4]、接收信号强度(RSS)[5]、信号到达角(AOA)[6]以及其他一些混合参数[1,7-8],并使用所选参量构建符合节点间几何关系的方程组。通过求解所列方程组得到移动节点的位置估计。

在实际的定位过程中,测量噪声是对传统定位算法定位精度造成显著影响的误差,其通常建模零均值的高斯变量[9]。除此之外,信号传播往往遭受障碍物遮挡导致非视距误差,这一类误差的概率分布模型往往无法准确建模。但在非视距NLOS(Non-Line Of Sight)传输环境中,非视距误差通常远大于测量噪声[10],信号到达角的测量值也显著偏离其真实值,因此对定位算法精度的影响非常显著[11]。鉴于此,针对非视距传输环境,研究人员提出了许多算法尝试抑制非视距误差的影响。例如NLOS误差识别算法。这一类方法就是对大量SN进行非视距误差检测分析,而后根据检测结果仅使用视距LOS(Line Of Sight)传输的SN进行定位[12],但是这类方法首先要求在通信网络中有足够数量的SN,同时必须有至少3个SN满足视距内传输的条件,对于NLOS误差影响比较严重的环境并不适用。另一类方法,例如残差加权算法(RWGH)以及约束最小二乘算法(CLS),就是从SN与MN之间的关系出发,以得到的距离测量值为基础构建最优化问题,通过求解最优化问题改善MN位置估计[13-16]。

本文在原始CLS算法基础上提出了一种改进定位算法,利用拉格朗日乘子法结合CLS算法的代价函数和约束条件来构建新的代价函数,并以此为基础得到新的最优化问题。进一步我们提出了分组定位组合的思路以进一步改善定位性能。仿真分析表明,在消除非视距误差对于定位精度的影响上,本文提出的算法优于对比算法。对仿真结果的分析还发现在NLOS误差较大时本文提出的算法将有更好的性能,同时本文提出的算法的性能也会随着SN数量的增加而进一步提升。

1 原始CLS定位算法

MS与BS之间的测量距离可以表示为:

ri=di+ni+δi,i=1,2,…,M

(1)

式中:ri为锚节点i与移动节点之间的测量距离,di为真实距离,ni为测量噪声,δi为NLOS误差。其中非视距误差通常是由障碍物阻碍信号的直线传播而增加信号的传播距离而产生的,而测量噪声的大小又远小于NLOS误差。则距离的测量值通常会大于真实值,即ri>di。

为了获得移动节点的位置估计,我们可以根据距离关系构建等式:

(2)

式中:(xi,yi)表示第i个SN的位置,而(x,y)表示需要定位的MN的位置。将公式两边取平方并移项,则可以得到

(3)

由于在NLOS环境中距离的真实值一定会小于等于测量值所以必有:

(4)

将其写成矩阵形式可以得到:

Y≥AX

(5)

因为在无误差环境下式(5)应取等号,则可以以等式两边的差值为参数构建代价函数,即

(Y-AX)TΨ-1(Y-AX)

(6)

根据以上推导,可以构建最优化问题:

min(Y-AX)TΨ-1(Y-AX)subject toAX≤Y

(7)

2 运用拉格朗日乘子法的改进CLS算法

2.1 最优化模型的改进

考虑到式(5)中矩阵X的元素x,y,R是相关的,即应满足:

x2+y2=R

(8)

然而为了求解的简便性,在原始CLS算法中没有考虑他们之间的相关性。实际上,由于受到测量噪声和非视距误差的影响,x,y,R之间必然有x2+y2≠R。因此以式(8)为基础构建新的目标表达式

XTpX+qX

(9)

我们可以将该目标以拉格朗日乘子方式融合到代价函数中,构建新的代价函数(Y-AX)TΨ-1(Y-AX)+λ(XTpX+qX),则改进CLS算法的最优化问题如下:

min(Y-AX)TΨ-1(Y-AX)+λ(XTpX+qX)

subject toAX≤Y

(10)

考虑到拉格朗日乘子法需要线性约束条件,因此使用加权最小二乘估计(ATΨ-1A)-1ATΨ-1YT替换最左侧的XT可以将式(9)转化为:

(ATΨ-1A)-1ATΨ-1YTpX+qX

(11)

再以式(11)为基础利用拉格朗乘子法构建拉格朗日函数:

(12)

式中:B=(ATΨ-1A)-1ATΨ-1YT+q,而H与c是原始代价函数中二次项与一次项的系数,在本文中H=2AΨ-1A,c=2YTΨ-1A。

令式(12)关于X,λ的偏导数等于0,即XL(X,λ)=0λL(X,λ)=0。

可以得到方程组:

HX+c-BTλ=0-BX=0

(13)

及其矩阵形式:

(14)

从上述方程组易解得λ=Rc-Sb,其中R=(BH-1BT)-1BH-1以及S=-(BH-1BT)-1。将他们代入(10)即可得到最终拉格朗日乘兹改进CLS定位模型。

2.2 分组定位方案

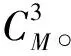
min(Yi-AiX)TΨ-1(Yi-AiX)+λ(XTpX+qX)

subject toAiX≤Yi

(15)

上述分组方法使得每一组节点组合均可以得到一个位置估计Xj,对这些位置估计的融合处理将得到更准确的位置估计。最简单的方式就是求所有Xj的质心:

(16)

现有仿真表明简单求质心可以一定程度提高改进CLS算法的性能,但是改进效果并不稳定,原因在于部分性能较差的节点组合显著影响了最终位置估计的性能。进一步分析后发现,这些所谓差的节点组合都无法覆盖移动节点可能存在的区域。因此论文采用了选择性的求质心方法,即先通过分组简单求质心得到MN初始位置估计,而后选择节点分组中能够覆盖MN存在区域的组合,并利用这些节点分组及其位置估计求质心:

(17)

这里N1是覆盖了初步估计位置的SN组合数量。最终的拉格朗日乘子改进CLS算法描述如下:

步骤1 将所有SN分组,每组3个SN;

步骤2 每一组SN基于式(14)获取位置估计Xj;

步骤3 所有Xj求质心获得初始MN位置估计;

步骤4 对每一组SN构成的三角形区域检测是否包含步骤3的初始位置估计,并选择具有包含性的SN组;

步骤5 对选中的SN组根据式(17)求质心获的最终的MN位置估计。

3 仿真结果

3.1 测距噪声与NLOS误差强度的影响

图1给出非视距误差在15 m～40 m上均匀分布时的定位误差累计分布函数(CDF),可以看出即使是表现最好的TOA CLS算法其误差也要大于本文算法。在CDF为0.9时,本文算法的定位误差相比其他算法至少小20%。

图2给出NLOS误差最大值不同取值对于定位性能的影响,其中MIN固定为15 m。从图中可以发现本文算法具有最小的平均定位误差,且定位误差差距大于0.5 m。这表明本文算法对于NLOS误差的适应性优于对比算法。

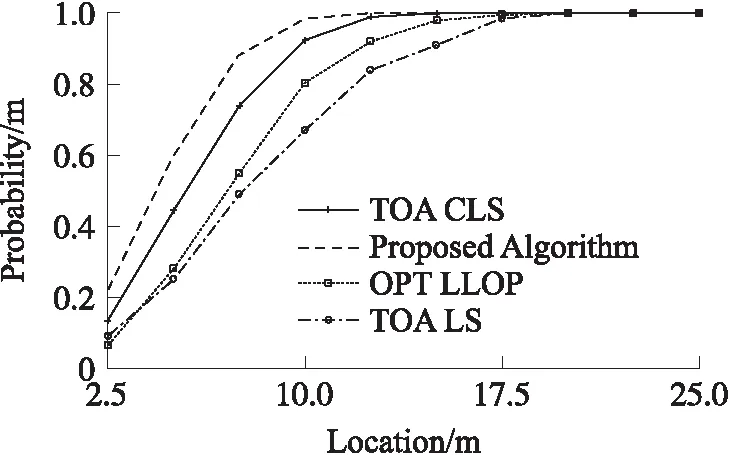
图1 NLOS误差服从15 m～40 m均匀分布时的累积分布函数

图2 不同MAX值对性能的影响

图3给出测距噪声标准差不同取值对于定位性能的影响,其中MAX=40 m。可以看到所有算法对于测距噪声标准差的敏感性都不强,但是本文算法具有最小的平均定位误差,定位误差的性能优势超过1 m。

图3 不同噪声标准差对性能的影响

3.2 SN数目对定位精度的影响

仿真中NLOS误差为15 m～40 m范围上的均匀分布随机变量,测距噪声标准差为1 m。考虑两个不同的SN数目:

增加两个SN,使得变成9基站分布,9个SN分别位于(0,0)(R,0)(R,R)(0,R)(-R,R)(-R,0)(-R,-R)(0,-R)(R,-R),CDF性能如图5所示。

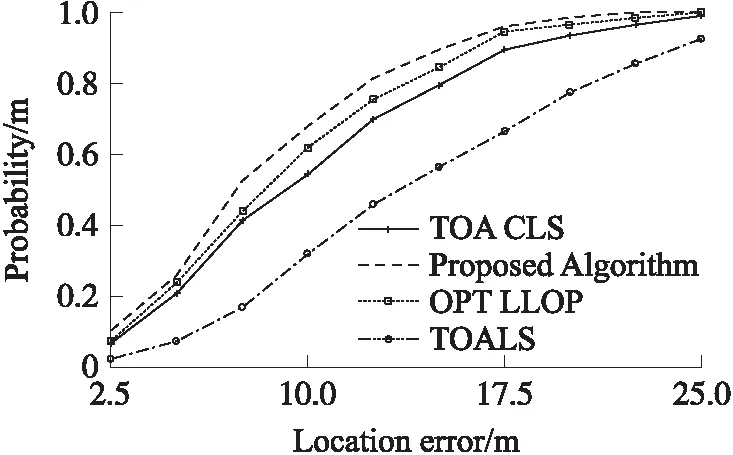
图4 5个SN时的算法性能对比

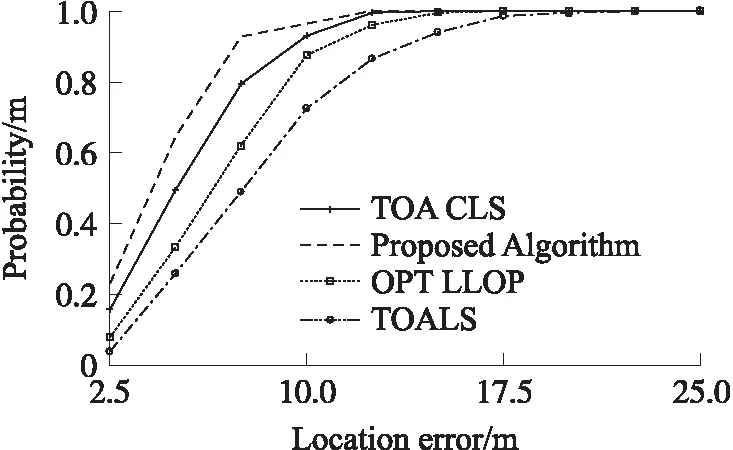
图5 9个SN时的算法性能对比

综合图1、图4和图5,可以发现本文算法在不同数目的SN情况下均具有最好的性能,且结果表明随着SN数目的增加,本文算法相较于对比算法的性能优势也会增加,从而可知本文算法适合工作于SN数目较多情形。

4 结论

非视距误差是影响无线定位算法精度的一个重要因素,它显著降低了定位算法的精确性。因此本文在传统约束最小二乘算法的基础上,利用拉格朗日乘子法构建了新的代价函数,并结合分组定位方案进一步改进定位精度。仿真结果表明,在不同强度的非视距误差和测距噪声下,文中所提出的算法都要优于对比算法,且本文算法随着SN数目的增加,可以提升相对于其他算法的优势。