水稻田面水氨氮的随机动力学模型探讨

王泽华 ，张一丁，孙颖娜

(1.哈尔滨市灌区管理处，哈尔滨 150020； 2.黑龙江大学 水利电力学院，哈尔滨 150086)

氨氮是重要的生命元素，是促进农业可持续发展的根本要素[1]。随着农业系统中大量使用化肥，在有效地增加粮食产量的同时，也增加了土壤中的氨氮含量。同时农田氨氮的流失量也在不断增加，从而带来环境风险问题[2-4]。我国水稻生产是主要农业生产之一，水稻田径流流失的氨氮在农业非点源污染中占有非常重要的地位。因此，研究水稻田中氨氮的迁移转化对于非点源污染控制具有重要的意义。人工湿地等生态工程被认为是控制非点源污染的有效措施，并被国内外广泛采用[5-8]。本文以人工湿地一级动力学模型为基础[9]，对水稻田面水氨氮的随机变化规律进行分析探讨。

1 随机模型的建立

1.1 基本原理

研究人员在对人工湿地去除氨氮等污染物的研究中，引入了一级动力学模型，该模型在人工湿地去污系统中得到广泛应用。本文在原有一级动力学模型的基础上，考虑其参数ke具有一定的随机性，在此基础上建立随机动力学模型，用以进行水稻田面水氨氮的衰减变化过程模拟。模型的数学表达式如下：

C(t)=aC0e-ket

(1)

式中：C(t)为氨氮、随时间t的衰减，mg/L；ke为反应速率常数，L/d；C0为营养物初始浓度，mg/L。

对式(1)两边取对数，则式(1)变为：

(2)

1.2 水稻田面水氨氮随机动力学模型的求解

将动力学模型中的反应速率ke看作一个随机变量，将利用各次试验的实测数据算得的ke作为随机变量的样本值，则式(1)是一个含有随机变量的动力学模型，可用来描述氨氮衰减浓度的随机变化过程。若随机变量k服从正态分布，则其概率密度函数为：

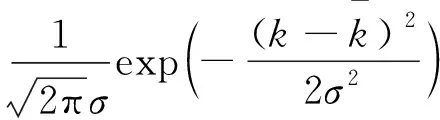
k∈(-,)

(3)

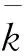
利用概率论和随机微分方程理论解得出流浓度的均值E(Ci)和方差D(Ci)过程为：

(4)

(5)

2 实例应用

2.1 数据来源

以黑龙江省绥化北林区秦家灌区试验区为研究区，应用随机动力学模型对实验数据进行分析，研究水稻田面水中氨氮的迁移转化规律。试验方式为通过对该试验区的3个小区进行氨氮浓度变化过程监测，试验数据为2007～2010年总计4年共12次施肥后实测得到的面水中氨氮变化过程数据。

2.2 水稻田面水中氨氮的速率参数率定

利用实测资料推求模型参数ke的样本值，实测资料采用2007～2009年的试验成果。参数ke值见图1及表1。

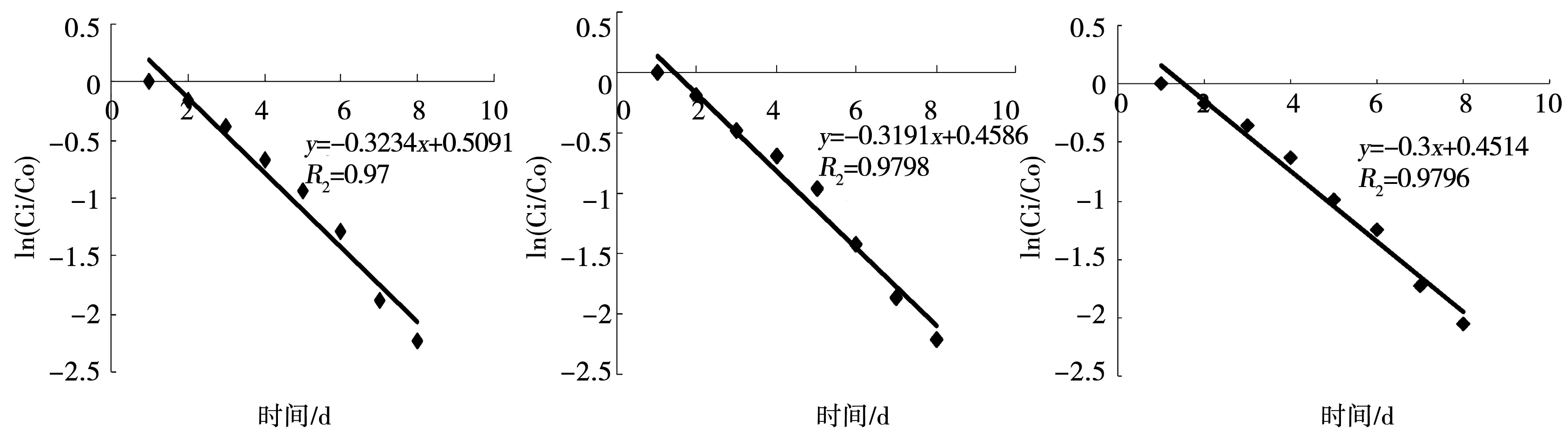
图1 水稻田面水中营养物反应速率参数(部分)

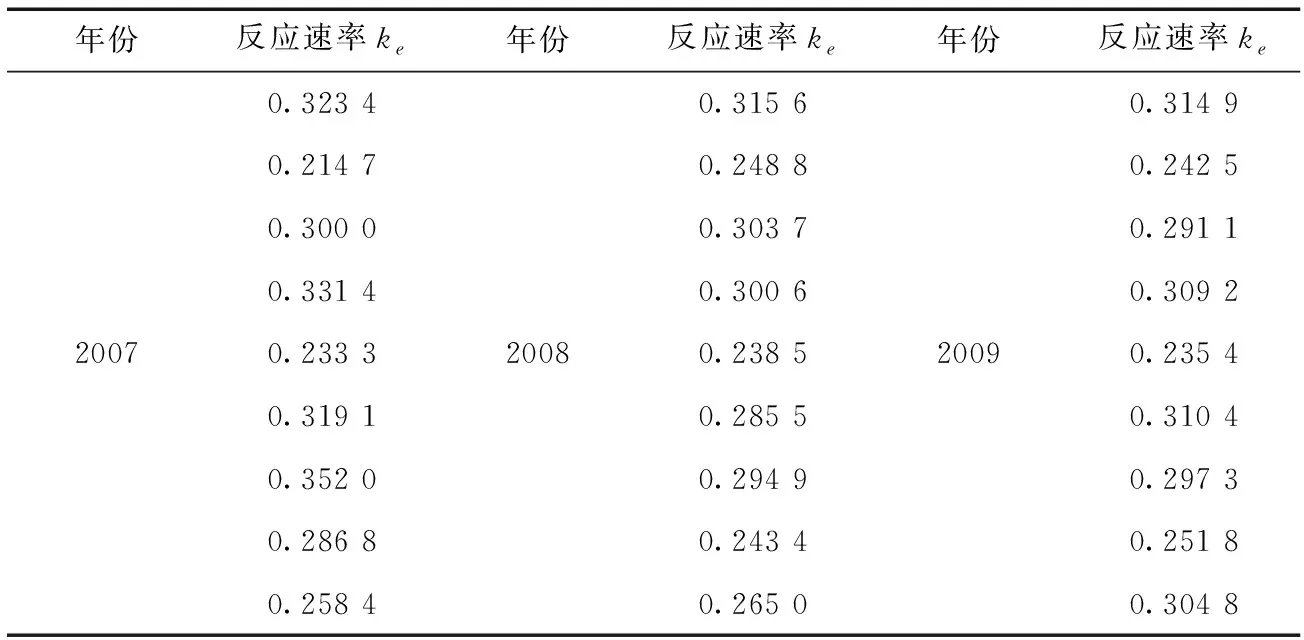
年份反应速率ke年份反应速率ke年份反应速率ke0.323 40.315 60.314 90.214 70.248 80.242 50.300 00.303 70.291 10.331 40.300 60.309 220070.233 320080.238 520090.235 40.319 10.285 50.310 40.352 00.294 90.297 30.286 80.243 40.251 80.258 40.265 00.304 8

对参数k采用χ2-优度拟合检验的方法进行假设检验，样本容量为n=27。结果表明，参数k服从正态分布。因此，考虑反应速率参数k为正态分布的随机变量是可行的，则可用式(4)、式(5)求解营养物浓度衰减的均值E(Ci)和方差D(Ci)过程。

2.3 水稻田水面氨氮模拟计算

图2 氨氮模拟计算与实测数值比较

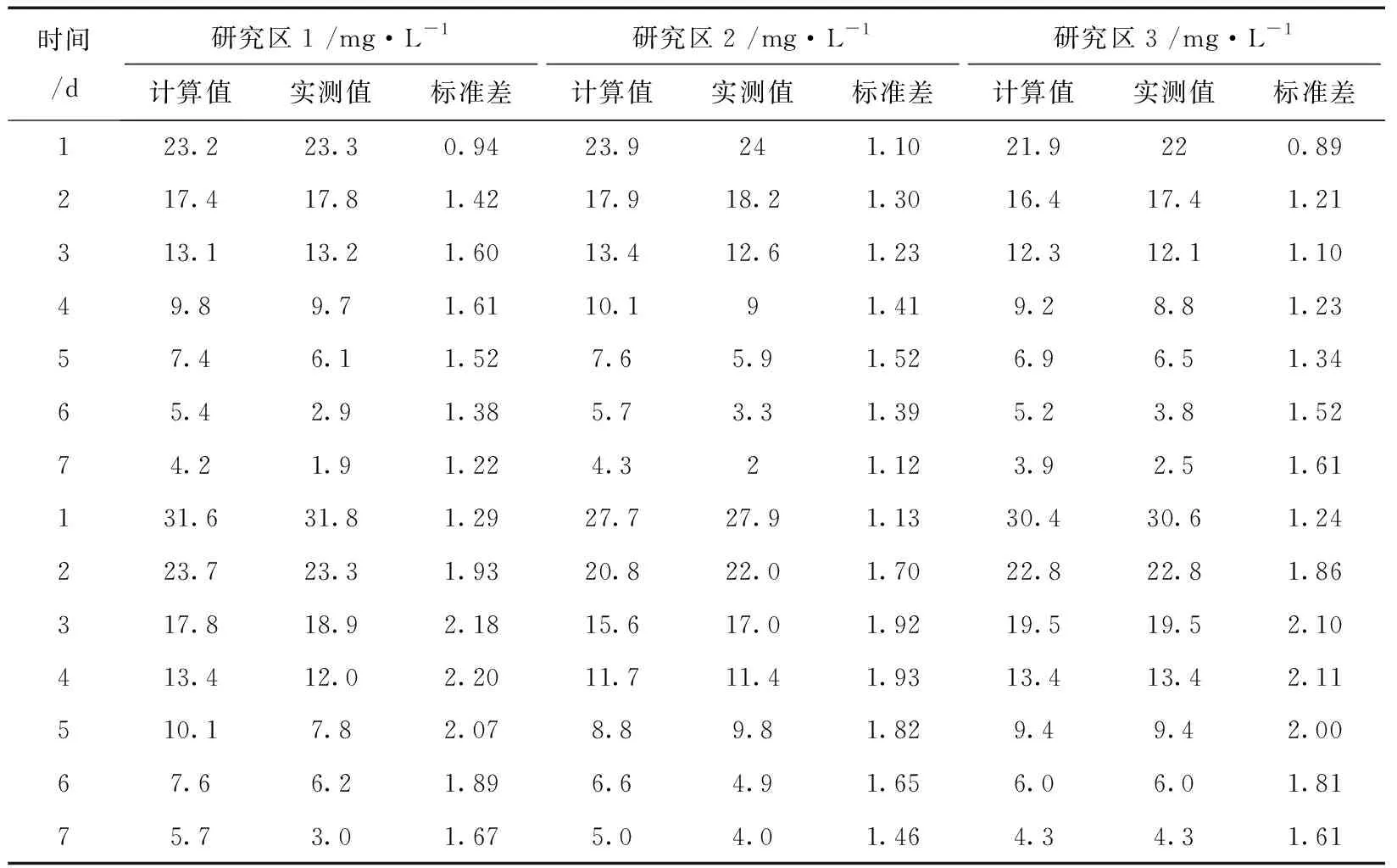
时间/d研究区1 /mg·L-1研究区2 /mg·L-1研究区3 /mg·L-1计算值实测值标准差计算值实测值标准差计算值实测值标准差123.223.30.9423.9241.1021.9220.89217.417.81.4217.918.21.3016.417.41.21313.113.21.6013.412.61.2312.312.11.1049.89.71.6110.191.419.28.81.2357.46.11.527.65.91.526.96.51.3465.42.91.385.73.31.395.23.81.5274.21.91.224.321.123.92.51.61131.631.81.2927.727.91.1330.430.61.24223.723.31.9320.822.01.7022.822.81.86317.818.92.1815.617.01.9219.519.52.10413.412.02.2011.711.41.9313.413.42.11510.17.82.078.89.81.829.49.42.0067.66.21.896.64.91.656.06.01.8175.73.01.675.04.01.464.34.31.61

3 结 论

本文以反应速率为随机变量，建立氨氮浓度衰减过程的随机动力学模型，应用试验数据，考虑反应速率为正态分布情况下对氨氮在水田施肥后一周内的衰减过程进行模拟。结果表明，应用该模型对氨氮在水稻田面水中的衰减过程进行计算，模拟过程符合实际规律，给出不同时刻的计算方差，可反映各时刻氨氮浓度的分布情况，进而反映模拟误差的分布规律，为农田面源污染控制提供科学依据，具有重要意义。