基于奇异谱分析法的GPS时间序列周期项探测
2018-08-30汤文娟
汤文娟
(1.广州市房地产测绘院,广东 广州 510030; 2.广州市测绘产品质量检验中心,广东 广州 510030)
1 引 言
高精度、实时的非线性运动特性研究和监测是大地测量学科的热门研究课题。只有在采用更完善的非线性运动模型的基础上,才能构建更高精度参考框架。
GPS参考框架点坐标变化具有复杂的非线性特征,很多经典的时间序列分析方法并不能有效地分离出不同尺度的周期运动特性,从而无法对所得结果给出合理的地球物理解释。奇异谱分析已经被证明为分解时间序列的有力工具,能弥补常用谱分析的不足。奇异谱分析方法的优越性主要在于①不需要预先给定滤波周期,只需根据资料自身确定,具有较强的自适应性。②对原始序列要求比较宽松,不需要对统计分布和平稳性做假设[1]。奇异谱分析方法根据序列自身的时间相关特性可以对序列进行动力重构,进行不同振荡频率的信号分离,在测绘领域中广泛用于序列插值、滤波去噪、趋势识别、周期项提取以及预报模型的建立。按照时间序列分析理论,每一个时间序列经过合理的变换后都可以分解为趋势项、周期项和随机噪声三个部分[2]。本文在时域和频域内,应用奇异谱分析对GPS连续观测站的位置变化情况进行分解,提取不同尺度的周期项,并与经典GPS时间序列模型最小二乘拟合结果进行对比。
2 奇异谱分析原理及周期项探测方法
2.1 奇异谱分析的基本原理
奇异谱分析(Singular-Spectrum Analysis,SSA)是时间序列中常用的分析与预测技术,组合了经典时间序列分析、多元几何、多元统计、动态系统和信号处理等多种元素。奇异谱分析将原始序列分解为缓慢变化趋势、周期项、噪声序列,基于时间序列的动力重构出发、与经验正交函数相联系,从事先未知物理本质的、包含噪声的有限长观测序列中,滤去非周期性的异常现象,对方差谱信号有强化和放大,将频域信号分解为时频信号加以识别和估计,提取尽可能多的可靠信息[3]。
应用奇异谱分析法研究分析框架非线性变化的特征,从框架点坐标序列中提取其周年运动、半周年运动等多时间、多尺度的非线性运动,从而构建非线性运动参考框架。对于长度N(N>2)的时间序列X=XN=(x1,…,xN),取窗体长度为L(1 (1)嵌入(Embedding) 嵌入过程是将一个一维的时间序列X=(x1,…,xN)转换为多维序列X1,…,XK,即将原时间序列映射为K=N-L+1个L滞后向量,时间序列X的L滞后轨迹矩阵X为: (1) 其中Xi=(xi,xi+1,…,xi+L-1)。 (2)轨迹矩阵的奇异值分解(SVD) 定义矩阵S=XXT,XT为X的转置矩阵。计算矩阵S的特征值λi和特征向量Ui,并将特征值按从大到小排列,其特征值依次为λ1≥…≥λL≥0,对应的特征向量为U1,…,UL。记Vi=XTUi(i=1,…,L)。其中Ui是矩阵的左特征向量,又称为时间经验正交函数(Temporal Empirical Orthogonal Function,T-EOF);Vi是矩阵的右特征向量,又称为时间主成分(Temporal Principal Components,T-PC),轨迹矩阵X可以由初等矩阵合成X=X1+…+Xd。初等矩阵为: (2) (3)特征值三要素分组 将初等矩阵Xi的下标{1,2,…,d}分成p个不相交的子集I1,I2,…,Ip,设I={i1,i2,…,im},那么合成矩阵XI=Xi1+Xi2+…+Xim,计算集合I=I1,I2,…,Ip的每个合成矩阵,那么序列的分解式可写为: X=XI1+XI2+…+XIp (3) 其中,选取集合I1,I2,…,Ip的过程称为分组。 (4)通过对角平均重构时间序列 奇异谱分析将序列分离成各种单一频率的振荡信号以及噪声项,利用时间主成分和时间经验正交函数展开各分量,可以获得对应于各频率振荡信号的重构分量序列,从而达到提取有用信息、过滤噪声的目的。将分组后的矩阵XIj重构为长度为N的新序列。设Y是一个L×K的矩阵,其元素为yij,其中1≤i≤L,1≤j≤K,L*=min(L,K),K*=max(L,K)且N=L+K-1,根据对角平均公式将矩阵Y转换为y1,…,yN的时间序列,对角平均公式为: (4) (5) (1)对应特征值接近相等; 以美国西北部阿拉斯加州观测质量好、精度高且稳定性强的GPS连续观测台站AV06为例,对其周期性运动特性进行分析,测站位置如图1所示。 图1 AV06观测台站位置分布图 根据实际分析处理经验所知,在周期项探测的过程中,用于分析的时间序列跨度和窗口长度L的选取对于分析结果有着很大的影响。如果需要分析序列中的年周期项或者更大尺度的周期项,则需要较长的时间序列,并且嵌入维数最好设置为周期的整数倍,这样可以获得较为精确的周期项信号。 对AV06观测台站的日观测坐标序列进行预处理,采用奇异谱插值法得到2005年~2016年12年间连续的3 902组日观测坐标序列,如图2所示。 图2 AV06台站日观测坐标序列 基于分析年周期的需要,在构造轨迹矩阵时,将嵌入维数设置为 1 500。分析特征值的分布情况,发现有几组明显成对的特征值,分别对前三对分量进行周期分析。周期探测结果如表1所示。 AV06-N主要成对RC的检验参数和周期 表1 综合三对RC分量的奇异谱分析结果,可以得出测站AV06在北方向上存在显著的年周期、半年周期信号。其他的RC成分在分析过程中并不满足周期波动成分检验的三条判别标准,暂时无法探测出其他周期成分。 (1)将第3、4主分量进行序列重构得到年周期项,并与最小二成拟合所得年周期进行对比,如图3所示。 图3 AV06-N年周期项对比图 其中,蓝色曲线为SSA分析所得年周期,绿色曲线为最小二乘拟合所得年周期信号。从图3中可以看出,经SSA分析,GPS时间序列中存在370天的周期项,即年周期项(由于频率设置的原因,如果频率之间的颗粒度更小,可以获得更精确的周期)。经SSA探测出的周期项与最小二乘拟合的周期项大体一致,但是最小二乘拟合结果为振幅恒定的周期振幅,而SSA所探测到的周期项振幅有随时间而增大的倾向。这对于框架的非线性运动特性研究有很好的指导意义,并且振幅逐年增大的趋势也可以反过来配合一些地球物理因素的解释,本文就不做进一步探讨。 (2)将第5、6主分量进行序列重构得到半年周期信号,并与最小二成拟合所得半年周期进行对比,如图4所示。 图4 AV06-N半年周期项对比图 通过周期图可以看出,GPS时间序列中存在175天的周期信号,即半年周期信号。半年周期对比图与年周期对比图相比,区别要更明显,这是因为SSA探测出的周期与半年有一定差距,随着时间的推移,两者半年周期信号开始出现峰值偏移。另外,奇异谱分析所得的半年周期信号的振幅除了有着明显随时间增大的趋势,其中也暗含着大约2.5年的周期项。这个现象有待进一步讨论。 对于AV06测站E、U方向2005年~2016年12年间的日观测坐标序列(共3 902组数据),构造嵌入维数为1 500的轨迹矩阵。分析特征值的分布情况,分别对前四对、前三对特征值明显成对的分量进行周期分析,分析结果如表2、表3所示。 AV06-E主要成对RC的检验参数和周期 表2 AV06-U主要成对RC的检验参数和周期 表3 从表2、表3中结果可以看出,测站AV06在E、U方向的分量坐标序列,除了常见的半年周期和年周期,还有1.5年周期、3年周期等等。由此可见,同一测站不同方向上坐标序列的周期性也不尽相同,但都含有近似年周期、半年周期项。 综合测站AV06三个坐标分量上的SSA周期探测结果,有以下两条结论: ①各分量序列中都含有半年周期、年周期项,除此之外,各坐标分量的周期性还有细小差别,即不同方向上的坐标序列可能还包含1.5年周期、3年周期,具体情形又略有不同。 ②跟最小二乘拟合结果有差异。奇异谱探测到的周期项并非振幅恒定,周期信号的振幅有随时间增大的趋势,并且在总体增大趋势中还暗含周期变化。 通过奇异谱分析方法提取出的周期项可知,不同测站的不同方向上的周期项也不尽相同,也不是严格的周年、半周年周期项,这些相近的周期项可能由同一个物理因素所引起,由于受分析方法的分辨率和定位精度所限,而表现出略微的差异[5]。下面对于周期性变化的几个主要影响因素进行分析。 (1)非模型化的地壳周期运动。奇异谱分析提取出的近似年周期、半年周期就属于地壳周期运动的结果。实验结果表明,GPS三个方向上时间序列并不存在严格的周年、半周年运动,而且不同测站之间的周期项具体周期值也互不相同。这种情况是由地壳运动的复杂性所致,也是严格的地壳周期运动与局部人类活动叠加的结果。 (2)测站周期变化。各种地球物理参数会对GPS测站时间序列中坐标有所影响,未模型化的固体潮、海洋潮汐以及大气质量负荷所引起的荷载会使测站表现出周期性变化。Amiri-Simkooei等[6]通过谐波估计,提取出很多介于170天~180天之间的周期项,刘伟、李昭等[5]也通过功率谱分析方法获得相似的结论,这恰好与Penna等给出的未模型化S2海洋潮汐荷载效应相吻合。 (3)多路径效应。由于GPS星座几何形状呈周期性变化,这导致多路径效应也呈周期性变化,而GPS星座周期性变化与计算GPS测站坐标所基于的太阳日之间存在约 247 s的差异,因此会产生350天的周期项[7]。因为本文中计算频率的精度在±0.000 1,因此提取出的周期项应该在338天~363天之间。 (4)周期性变化的潜在因素。SSA所探测出的长周期项没有物理背景所对应,可能是由其他很多潜在的影响因素所导致的,比如台站下基岩的热膨胀、天线相位中心模型误差、对流程湿分量影响、轨道模型误差等等[8]。 关于所探测出的周期结果,本文并未做进一步探讨,但是可为参考框架点的非线性运动研究提供一定的数据支持。同时,这样的周期变化特性又该如何结合实际的地球物理因素给出模型化的改正,这也是有待解决的问题。



2.2 基于SSA的周期项探测
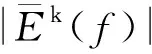
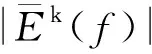

3 GPS坐标序列中周期项探测


3.1 AV06测站N方向的周期项探测



3.2 AV06测站E、U方向的周期项探测


4 周期项影响因素分析
