基于特征价格理论和神经网络的武汉二手房价自动评估

陈敏，李英冰

(1.武汉大学测绘学院，湖北 武汉 430079； 2.武汉大学测绘学院时空大数据研究中心，湖北 武汉 430079)

1 引 言

在房地产税制改革和大数据的背景下，我国的房地产评估行业面临新的挑战[1]。许军等指出我国房地产评估行业的目标应由“以房为本”、“服务开发”的模式转变为“以人为本”、“服务两端”的模式[2]。“以人为本”要求从消费者需求的角度出发考察影响房价的因素，将其作为房价评估依据；“服务两端”强调建立统一管理平台，为消费者和政府相关部门提供经济、高效的优质信息服务。

目前，国外已经有了基于CAMA (Computer Assisted Mass Appraisal)和GIS(Geography Information System)的房地产批量评估方法，而我国仍处于大数据系统的构建阶段[2]，缺少相关的技术、算法支持。特征价格理论认为住宅价格的确定不是基于作为整体的住宅本身，而等于住宅各个属性的效用总和[3]，呼应了“以人为本”的需求；人工神经网络作为一个强大的非线性变换系统[4]，具有自组织、自学习的特点，能够充分利用大数据优势，在实例研究中显现出较传统方法更高的准确率和效率[5～9]，或许能在自动批量评估系统中发挥重要作用。因此，综合特征价格理论和人工神经网络，探索更准确、效率更高的估价算法，能够提高估价方法的科学性和前瞻性，并推动统一的房地产信息服务平台的构建。

2 数据处理与模型构建

2.1 研究区域

如图1所示，研究区域为距离武汉市政府 15 km的武昌、江汉、洪山、青山、江岸、硚口、汉阳七个行政区内的212个小区。各小区与市中心联系紧密，基本在三环线内。各小区平均二手房价格 3 714 元/m2～22 112 元/m2不等，小区内不同房屋成交价也有差别。

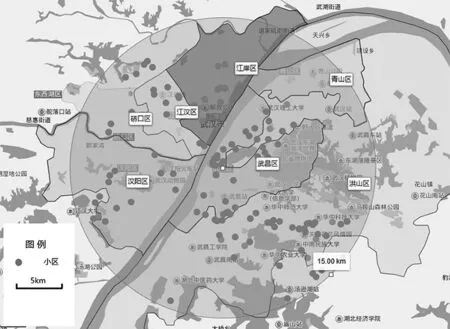
图1 研究区域及小区分布

2.2 基于特征价格理论的样本数据整理

特征价格模型的一般形式[4]为：

P=f(X1，X2，…，Xi)

(1)

其中P为住宅价格，Xi表示住宅特征，f为特征与价格之间的函数关系。

住宅特征(即房价影响因子)的选取十分重要，特征价格理论默认模型仅包含影响房价且量测精确的因素。但是，影响房价的因素十分复杂，且存在随机波动；加上某些特征不能做到精确测量和量化，实际难以达到这一标准。

王娟娟等[10]统计了相关文献中常用的特征变量及其显著性，为特征变量的选取提供了参考。根据此参考及数据库数据，结合武汉市房地产市场特点，确定了参与评估的14个特征变量，如表1所示。

特征变量及数据来源 表1

量化数据时定量特征直接引用数值；定性特征则采用二元虚拟变量法、李克特量表法或综合性指标法量化[11]。再手动补充、剔除缺失值、删除虚假数据、剔除异常值，最终得到武汉市二手房数目多于200套的住宅小区212个，小区内部二手房样本 84 215条。

2.3 人工神经网络分级模型搭建

利用神经网络估计住宅价格，思路是把住宅的各个特征变量作为输入，房价作为输出，把各个特征变量与房价之间的关系模拟为各层神经元之间连接的权值与阈值。通过大量样本的监督学习，得到合适的权值与阈值，即确定了特征变量与房价之间的关系。

部分利用神经网络进行估价的研究采用的训练样本体积偏小，并且只给出一个通用网络模型，没有考虑空间异质性对模型精度的影响，如周围是否有学校很大程度影响到购房决策[12]。不考虑小区间这类影响因子的差异，模型的泛化能力无法得到保证，难以应用于实际。考虑到随着样本体积增大，网络训练的速度降低，效率不高[13]，本文设计了整体基准价和精确估价的两级模型，结构如图2所示。抽取研究区域的样本训练得到基准价网络，再输入需要估价的小区样本进一步训练得到适合该小区的精确估价网络，希望在保证模型的泛化能力同时提高估价效率。

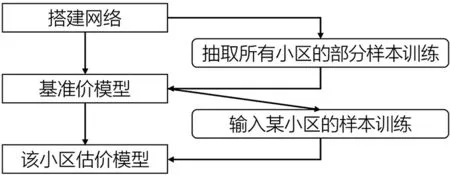
图2 分级模型结构

基准价模型和精确估价模型的构建涉及网络结构、激活函数确定，训练算法选择的工作。其中，隐层节点个数、激活函数以及学习速率可以基于经验和试凑法确定，通过随机抽取5 000条样本进行实验，不断调整学习速率，确定最优隐层节点数为30，激活函数第一层为logsig，第二层tansig。网络的训练采用反向传播的思想。对每一个样本(x，y)，(x为特征向量，y为价格)先进行前向传递，求每个神经元的激活值a，得到估价h(x)。

a=∑σ(ωx+b)

(2)

再比较h(x)与真实价格，利用损失函数求损失C(函数cost通常是均方误差)。

C=cost[h(x)，y]

(3)

接着进行误差反向传播，从最后一层向前依次求各层误差(链式法则)，并调整权值和偏置(式(4)、式(5)运用的学习算法是梯度下降)。反复迭代至C足够小，停止训练。

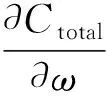
(4)

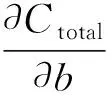
(5)

反向传播有梯度下降法、拟牛顿法、共轭梯度法和Levenberg-Marquardt法等经典算法。不同训练算法最小化损失函数的思想不同，在收敛速度、计算量、泛化能力上存在差异，因而针对不同参数规模的网络应选取不同的训练算法[14]。

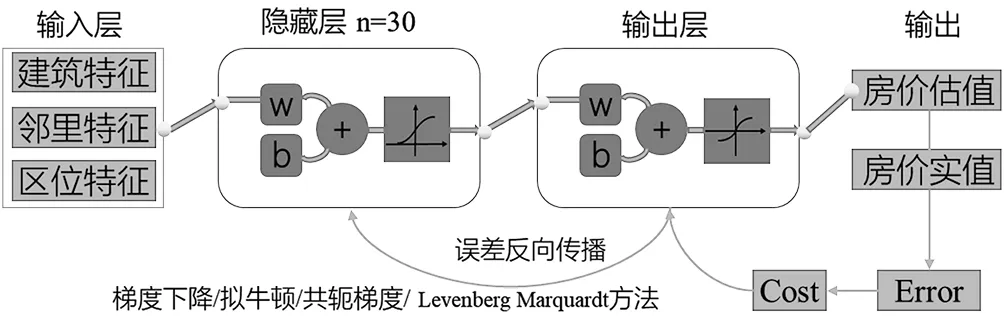
图3 网络结构及训练思路

本文影响因子数较少(14)，网络参数不多(481)，但样本体积较大(84 215)。 图3展示了网络结构和训练思路，为确定最优训练算法，抽出“武汉天地御江璟城”小区数据，将其余 83 871条样本分为训练组(80 000条)和测试组(3 871条)输入网络用不同算法分别训练，综合比较模型训练时间、估价结果精度(如表2所示)得到合适的训练算法。

3 结果及分析

模型评价采取拟合优度R2和估价相对误差RE、绝对误差AE。拟合优度评价模型对观测值的拟合程度，越接近1效果越好；相对误差与绝对误差能更直观地表现估价精度。

R2=(TSS-RSS)/TSS

(6)

AE=h(x)-y

(7)

RE=AE/y

(8)

其中，TSS为总误差平方和，RSS为残差平方和。

用不同训练算法训练基准价网络得到估价结果，如表2所示，比较结果的拟合优度、平均相对误差、相对误差在10%、20%内的样本比例，梯度下降法和共轭梯度法均陷入了局部最优解，模型精度低；拟牛顿法精度虽高但不及L-M法，且训练时间过长；L-M法估价精度高、收敛速度快，训练时间适中，最合适。

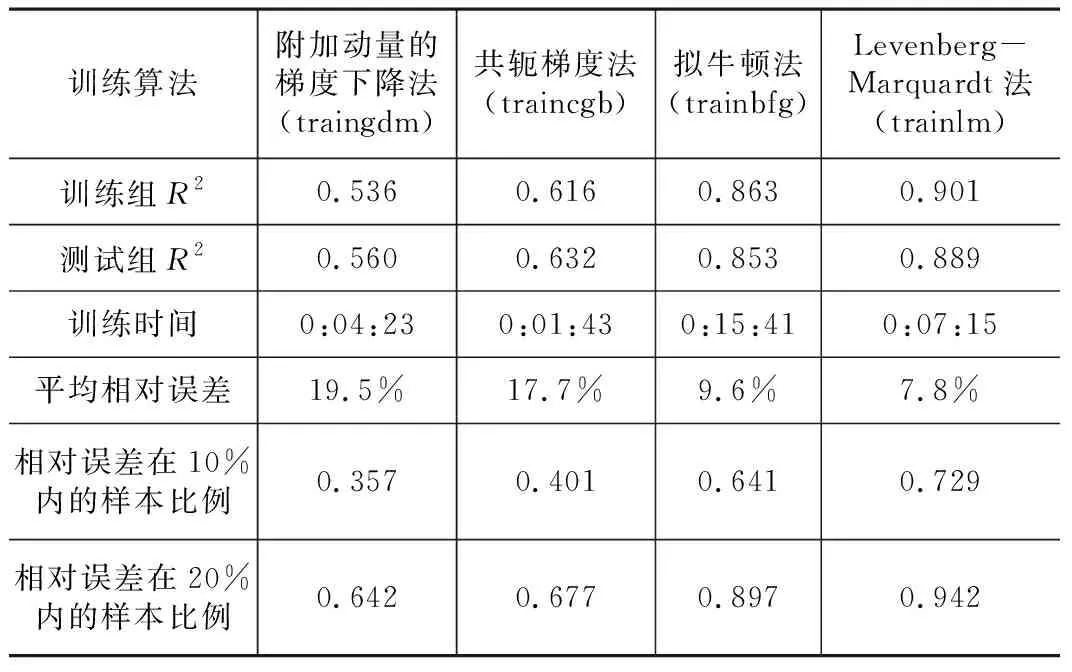
基准价网络不同算法估价结果 表2

在基准价网络上进一步输入特定小区的二手住宅样本进行小区估价模型训练，这里以两个小区(如表3所示)为例，给出估价结果的相对误差(如表4所示)。小区武汉天地御江璟城在江岸区，所有样本没有参与基准价网络训练，小区世纪江尚在江汉区，均价低于武汉天地，部分样本参与了基准价网络训练。

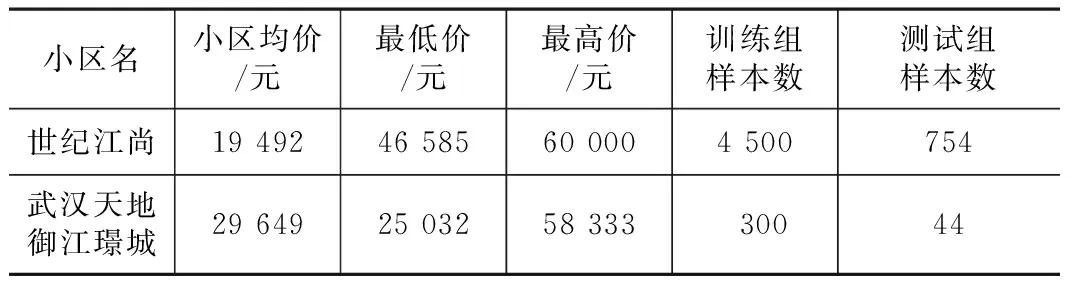
小区价格分布及样本数量 表3

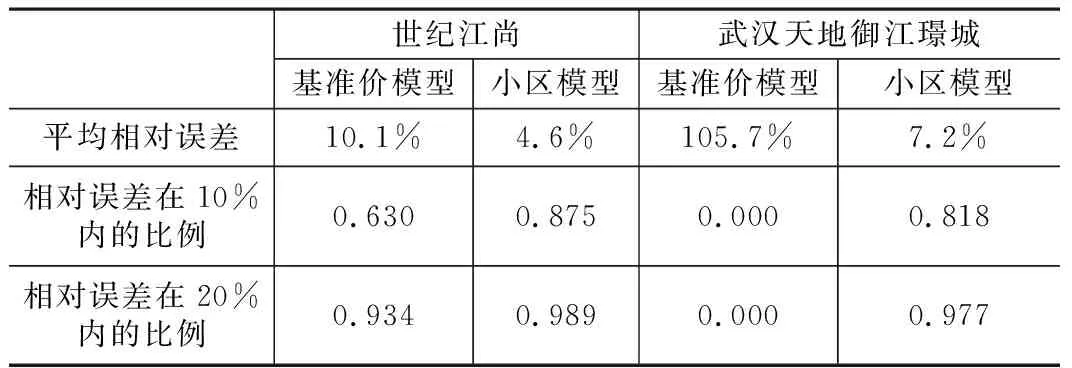
小区估价模型精度比较 表4

如表4所示，小区模型的估价精度均优于基准价模型，说明分级模型对精度有提高作用。在训练世纪江尚的小区模型时，迭代10次便达到了表中的精度，证明在基准价网络上训练模型，能够提高效率。世纪江尚的部分样本参与了基准价模型训练，用基准价模型直接估价时，平均相对误差小；武汉天地的样本没有参与基准价网络训练，直接用基准价模型平均相对误差达到了105.74%，说明将小区样本纳入基准价模型的必要性。整体上看，两个小区模型估价结果的相对误差在20%内的比例均达到了95%以上，具备实际应用能力。

4 总 结

本文应用特征价格理论确定14个房价影响因子，与神经网络结合，建立了武汉市二手住宅估价的两层分级模型。一方面，在基准价网络基础上训练针对特定小区的网络，训练时间缩短，提高了效率；另一方面，通过将所有小区的部分样本纳入整体的基准价模型，可以保证模型的泛化能力，再训练特定的小区估价模型，能够提高估价精度。此分级模型为自动批量评估系统的实现提供了一种可行思路。

对于面向海量数据的房价自动评估系统，要进一步提高估价精度，除探索效率更高的估价算法外，可从数据着手，提高输入的数据质量，这一点或可通过引入有效的异常点自动挖掘算法实现。