含螺栓连接结构的非线性静力学拓扑优化

张晓頔， 郝志明， 李一堃， 刘远东

(1.中国工程物理研究院总体工程研究所， 四川 绵阳 621900； 2.成都大学高等研究院， 成都 610106)

连接结构在航空航天、军事装备和核电等领域中均有广泛应用[1-2]，大型装备如航天器、军用车辆、反应堆压力容器等是由不同的零部件通过螺栓预紧连接、铆钉连接、楔环连接等多种连接方式连接而成。在结构系统的拓扑优化设计中，认为连接结构的接触表面不发生相对运动，将其简化为线性模型分析，计算效率更高。实际上连接结构的刚度和阻尼具有不连续性、迟滞性等非线性特性，分布于结构系统不同位置的刚度不同，对整体结构的力学特性的影响也不同[3]。由于连接接触界面在外载荷作用下发生微观滑移现象甚至宏观滑移现象，引起能量耗散并产生干摩擦阻尼，占结构整体阻尼的90%；同时连接接触界面的滑移还会引起结构局部刚度非线性变化。因此，在对复杂工程结构开展拓扑优化研究时，考虑其连接部分的非线性具有重要的意义。

结构拓扑优化研究经历了从离散体结构到连续体结构的发展过程。从早期由Michell的桁架理论和Dorn等人提出的基结构法建立起离散结构的拓扑优化方法，发展到由Bends?e和Kikuchi提出的结构拓扑优化设计均匀化方法，标志着连续体结构拓扑优化设计的诞生。Xie[4]又提出了一种连续体拓扑优化方法——渐进结构优化方法(Evolutionary Structural Optimization，ESO)，与均匀化方法相比，它不产生0-1之间的中间密度，拓扑形式清晰，也避免了多变量的数学规划求解，这种方法已成功应用于大量工程优化问题的求解。目前关于线弹性材料和小变形的结构拓扑优化研究较为充分，但考虑结构非线性行为的研究仍相对较少[5]。Ryu等[6]率先进行了非线性响应的设计灵敏度分析，开辟了非线性结构优化研究的先例。Buhl等[7]研究了几何非线性结构的拓扑优化，指出非线性和线性情况下优化结果的区别。Yuge等[8]将材料非线性引入结构拓扑优化，改进弹塑性均匀化方法，提高了计算效率。Jung等[9]在优化中同时考虑了几何非线性和材料非线性，进行了数值验证。考虑界面非线性的结构优化研究文献很少，仅在尺寸优化和形状优化方面有少量工作[10-11]，尚未见界面非线性问题的拓扑优化研究报道。

开展含螺栓连接结构的非线性拓扑优化设计，需模拟连接界面的接触行为。传统摩擦模型[12]如库伦摩擦模型在有限元分析中主要采用接触算法，计算较为耗时且不易收敛，难以应用于拓扑优化分析。因此，寻求一种更加合理的模型描述连接界面的接触行为十分必要。连接接触本构模型[13]是一类能描述摩擦接触非线性迟滞行为的模型，如Iwan模型、Bouc-Wen模型、Valanis模型和剪切层模型等。其中Iwan模型[14-15]由一系列理想弹塑性元件组成，最初用以描述金属材料的弹塑性力学行为。Segalman[16]最早采用并联-串联形式的Iwan模型描述连接接触非线性力学行为，提出了一个四参数Iwan模型，能够准确反映微观滑移能量耗散的幂次关系，但不能描述发生宏观滑移后的残余刚度现象。在四参数Iwan模型的基础上，Li等[17-18]提出了一个含截断幂律分布和双脉冲的非均匀密度函数的六参数Iwan模型，可以同时描述微观滑移阶段能量耗散幂次关系和宏观滑移阶段残余刚度现象。此外，该模型引入有限元分析，不需要采用接触算法，计算易于收敛[19-20]。

本文旨在建立一种含界面强非线性的静力学拓扑优化方法。采用六参数Iwan模型描述含螺栓连接的非线性力学行为，ESO方法结合结构非线性分析，用ANSYS软件的参数化设计语言(APDL语言)编写命令流文件，形成一套优化算法，应用于含螺栓连接圆筒结构的拓扑优化设计。

1 螺栓连接的非线性力学模型

Iwan模型由若干Jenkins单元(弹簧-滑块)构成。图1所示为并联-串联型Iwan模型，其中ki为弹簧单元的刚度，fi为滑块单元的屈服力，F和u为外力和位移。令每个Jenkins单元的刚度均为k，位移载荷为x，单元屈服力f以密度函数r(f) 表示，可以得到Iwan模型表达式如下：

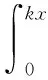
(1)

将式(1)对x求二阶导数后整理得

(2)

再令φ=f/k,ρ(φ)=k2r(f)，则式(1)可改写为

(3)

(4)

式中ρ(φ)为密度函数。Li等[17-18]提出一个含截断幂律分布和双脉冲的非均匀密度函数，如图2所示，其表达式为

(5)

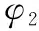
将式(5)代入式(3)中积分可以得到六参数Iwan模型的力-位移曲线关系，其示意图见图3。O-A段力-位移关系呈线性；A-B段为微观滑移阶段，力-位移关系呈非线性；从B点开始模型进入宏观滑移阶段，力-位移关系再次呈线性。

将六参数Iwan模型应用于数值计算时，将其离散为n+2个并联的Jenkins单元，如图4所示[20]。前n个Jenkins单元J1～Jn描述微观滑移阶段连接结构刚度的变化；第n+1个Jenkins单元Jn+1描述宏观滑移时刻刚度的变化量，其刚度为K2；第n+2个Jenkins单元Jn+2为描述宏观滑移后接触界面残余刚度现象的弹簧单元，其刚度为K∞。

2 考虑接触非线性的渐进结构优化

一个理想的结构，其每一部分的应力应该接近于相同的安全水平[21]。而受力分析表明结构中的应力分布并不均匀，可以认为应力水平较高的区域是结构破坏的主要区域，而在应力水平较低的区域材料处于没有充分利用的状态。以单元的等效应力作为删除判据，将低应力的材料逐渐删除，更新结构设计，使得优化后的结构应力水平更加均匀，材料构成趋于合理，同时也提高了材料的利用率。对于各向同性材料可采用von Mises应力作为单元删除判据。

(6)

式中Sij为应力偏张量，且i=j。

(7)

则认为该单元处于低应力状态，是无效的或低效的单元，对结构整体性能贡献最小，应从结构中删除。

保持当前删除率不变，重复删除单元，直至再无单元满足式(7)，即优化结果对于当前删除率RR已达到稳定状态。此时引入一个进化率ER，将删除率修改为

RR=RR+ER

(8)

以新的删除率重复删除和更新删除率过程，直到结构满足给定的约束条件为止。

含螺栓连接结构的拓扑优化的约束条件应包括两个方面：1)结构的强度要求，即结构的应力不超过许用应力；2)结构的连接刚度要求，即一般不允许螺栓连接界面产生宏观滑移，造成螺栓受剪切载荷作用。以结构的质量最小为目标函数，结构的最大等效应力满足要求、连接不产生宏观滑移为约束条件，以设计区域材料单元的存在状态为设计变量，建立如下拓扑优化数学模型：

(9)

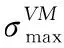
基于应力水平的含螺栓连接结构的非线性渐进结构优化方法的步骤如下：

1) 建立含螺栓连接的组合结构非线性有限元模型。利用六参数Iwan模型描述螺栓连接界面的非线性特性；定义载荷及边界约束条件；

2) 确定优化准则。本文采用应力准则，如式(7)；

3) 定义初始删除率RR和进化率ER；明确结构的许用应力和螺栓连接处相对位移(滑移量)允许值；

4) 采用增量法分步施加载荷，对当前离散结构进行非线性静力学求解；依据当前删除率RR，将满足式(7)的低应力单元组成集合Ωσ，删除集合中的单元；

5) 保持当前删除率不变，重复步骤4)，直至再无单元满足优化准则，即优化结果对前删除率RR已达到稳定状态。此时引入进化率ER，按式(8)对删除率进行修改；

6) 以新的删除率重复步骤4)～5)，直到单元最大等效应力达到许用应力或螺栓连接处的相对位移达到允许值，优化完成。

3 算例

3.1 模型的建立

图5(a)所示为一含螺栓连接的圆筒组合结构，由圆筒和底座两个部分组成。底座上半部分为一内径120 mm、外径370 mm、厚度10 mm的圆盘，其上表面与圆筒连为一体，下半部分为直径370 mm、厚度10 mm的圆板。三对单螺栓连接组件以120°间隔均匀排布在直径为300 mm的圆周上，将底座上下部分连接起来。螺栓预紧力为7 117 N(图5中未画出连接螺栓)；圆筒高为335 mm，内径为230mm，外径为234 mm，厚为2 mm。结构材料为钢材，弹性模量=200 GPa，泊松比ν=0.3，密度ρ=7 850 kg/m3，许用应力σ*=105 MPa。

有限元建模采用SOLID185单元，以六面体网格将结构划分为31 412个单元，如图5(b)所示。

文献[23]对预紧力为7 117 N时的螺栓连接实验结果进行了参数辨识，具体值见表1。将表1的参数代入六参数Iwan模型，获得如图3所示的单个螺栓连接的力-相对位移关系(骨线方程)。图3B点为宏观滑移的起始点，对应的力为4 430 N，相对位移φ2=1.02×10-5m。若取不发生宏观滑移的安全系数[n]=1.2，则允许的最大相对滑移量Smax≤0.85×10-5m。

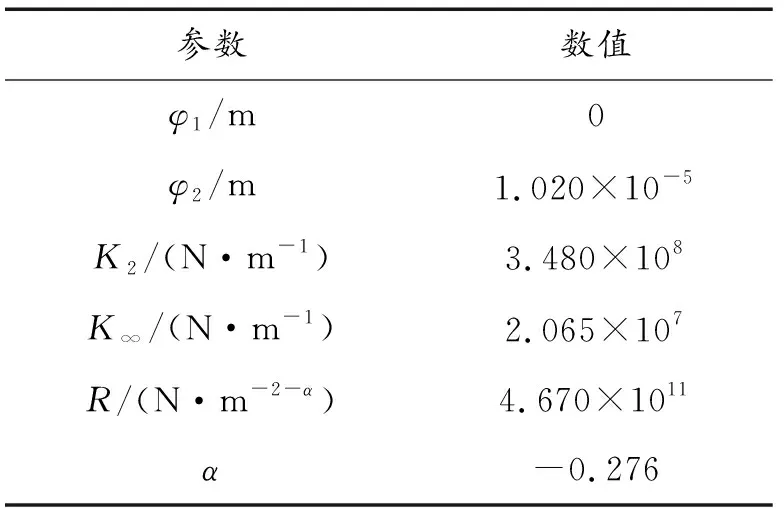
表1 预紧力7 117 N的参数辨识结果

3.2 拓扑优化

在ANSYS有限元分析中，每对螺栓连接组件之间均以六参数Iwan模型描述，将每对连接离散为13个COMBIN40单元和1个COMBIN14单元(图4)，各单元的单元刚度和屈服力的选取参见文献[23]，APDL命令流如下。

/prep7

!定义单元类型!

et,1,40

et,2,14

!定义单元的刚度和屈服力!

R,1,1.31E+07,,,,2,,

R,2,1.31E+07,,,,8,,

R,3,1.31E+07,,,,15,,

R,4,1.31E+07,,,,24,,

R,5,1.31E+07,,,,35,,

R,6,1.31e+07,,,,46,,

R,7,1.31e+07,,,,57,,

R,8,1.31e+07,,,,70,,

R,9,1.31e+07,,,,83,,

R,10,1.31e+07,,,,97,,

R,11,1.31e+07,,,,111,,

R,12,1.31e+07,,,,126,,

R,13,3.48e8,,,,3549.6,,

R,14,2.065e7,,,,,,

!将1-13号单元设置为类型1!

*do,rin,1,13

type,1,

real,rin

e,m,n

*enddo

!将14号单元设置为类型2!

type,2,

real,14,

e,m,n

(说明：命令流中m和n分别为每对螺栓连接的两个接触面中心节点的编号。)

约束底座下端面，对筒体上端面施加7.5 MPa的均匀压力，并选定初始删除率RR=0.2%，进化率ER=0.1%。利用编写的命令流输入文件，完成非线性求解、优化循环及后处理等过程[22]。

优化后的圆筒结构如图6所示，最大等效应力为105 MPa(对应删除率为60%)。最终优化构型中肋条的上部沿圆周均匀分布，承受加载在筒体上端面的均布载荷；下部与螺栓连接结构的排布相对应，呈120°分别集中，、向下方的连接部分传力。很明显，优化后得到拓扑构型很好地反映了结构的受力和传力特征。

表2中列出了随删除率的增大，筒体的单元最大von Mises应力的变化。从表2可以看出，筒体的最大等效应力随删除率增加而逐渐增大，当删除率达60%时，筒体最大等效应力达到许用应力，此时连接单元的相对滑移量Smax=8.12×10-6m，小于允许的最大相对滑移量8.5×10-6m，即连接处没有产生宏观滑移。

表2 筒体应力随删除率的变化

4 结论

本文采用六参数Iwan模型描述螺栓连接的非线性力学行为，再基于渐进结构优化方法和非线性有限元分析，建立含螺栓连接圆筒结构的非线性静力学拓扑优化方法。利用ANSYS软件中的APDL语言编写命令流输入文件，实现优化流程。通过含螺栓连接圆筒组合结构的优化算例，验证了含界面强非线性的静力学拓扑优化方法可以应用于含螺栓连接复杂工程结构的静力学拓扑优化设计。