基于改进双层规划的常规导弹多波次作战路径优化

吴闰平,刘卫东,杨 萍

(火箭军工程大学， 西安 710025)

随着各国军事科技的飞速发展，导弹武器以其射程远、精度高、威力大、隐蔽性强等诸多优点成为打击敌方军事要地、政治中心和重要设施的重要手段之一。多波次、大弹量的常规导弹打击，涉及到导弹的机动运输，如何设计较优的机动路径，使得导弹发射装置以最短的时间机动至相应阵地，减少暴露时间，增加生存概率，有效提高导弹部队战斗力。

对于多波次作战中的机动路径规划,前人也做了相关的研究，汪民乐[6]研究了多波次对地攻击的火力分配问题；王桐[7]运用马尔科夫链解决了多波次打击敌方目标的效果评判问题；杨萍[5]运用军事运筹学与不确定理论对多波次导弹打击的战前运输进行了建模分析，王鹏[8]根据军事公路运输的特点，建立了基于GIS的路线选择模型，给出了相应的求解方法。总体来看，前人所做的研究主要集中在导弹发射装置的机动路径优化方面以及在给定机动路径的基础上进行机动调度，解决了多波次导弹作战的路径规划与机动调度基本问题。但考虑到在计算好机动路径的基础上进行机动调度，缺少了机动路径最短与机动时间最短的良好反馈，难免存在较大的机动冲突，延长机动时间，增加暴露风险。因此对于机动路径与机动时间要进行同时考虑且相互反馈，才能达到最优的机动方案。

本文作者考虑到导弹多波次作战时对时间要求较高，因此对一般的双层规划模型进行了改进，上层建立了路径最短的多波次打击优化模型，下层建立了时间最优的多波次打击优化模型，并且上层与下层本身也是一个双层规划模型，通过上层的上层与下层的反馈使得总的机动距离最短，在此基础上进行机动调度，下层的上层与下层进行反馈调整使机动时间最短。如果出现最短的机动距离导致大量机动冲突，则下层反馈至上层进行重新优化，直至得到较优的机动距离与最优的机动时间。

1 模型建立

模型假设：1)对于给定的发射装置，在给定的路径上行驶时，行驶速度为定值，遇到路径冲突时，可以通过节点等待的方法解决；2)单行道不能出现超车、会车的情况，双行道或者多行道可以超车、会车；3)所有发射装置到达发射点位的时刻不尽相同，但通过在发射点位等待，所有发射装置进行齐射；4)开始时刻，我方发射装置处于待机阵地伪装防护较好，未从待机阵地机动出来的发射装置不算在暴露范围之内；5)在转载过程中，我方发射装置处于较好的隐蔽点位，在整个转载区域的发射装置不算在暴露范围之内。

对于多波次打击问题，其作战基本流程为：导弹发射装置从待机阵地机动至发射阵地进行第一波次发射，在完成第一波次发射任务后，发射装置从发射阵地机动至转载阵地进行转载装填，完成后再次机动至发射阵地进行第二波次的发射，其中第二波次的发射阵地不能与第一波次的发射阵地重复使用，以免在已经暴露的发射阵地发射时遭受敌方的精确打击，之后多波次的发射流程与前两个波次相类似。作战流程如图1所示。

在整个发射过程中，不仅要求导弹发射装置机动路径最短，同时也要求发射装置在机动过程中机动时间与节点等待时间之和最短，而路径最短的目的是为了机动时间最短，但在部分条件下，最短路径机动方案可能会多次重复使用部分道路，使得被重复使用的道路交通压力变大，导致整体机动调度较为困难，发射装置在机动过程中冲突较多，等待时间变长，增加暴露时间。运用双层规划理论并进行改进，上层为机动路径优化模型，下层为机动时间优化模型，上层和下层的优化模型又分别是一个双层规划模型，分别对多波次的机动路径与机动时间进行优化。

多波次打击与双波次打击基本类似，因此首先对于两个波次的打击进行建模分析，之后对其进行推广即可得到多波次作战模型。要求第一波次与第二波次的机动路径都要尽可能短，即

(1)

(2)

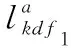
同时，第一波次与第二波次的机动时间也要尽可能短。

(3)

(4)

在对得到的机动方案进行机动调度时，在该路径上行驶所用时间为该路径的距离除以该路径上行驶的发射装置机动速度与该路径上等待时间的和，即

第一波次所用时间为：

(5)

第一波次发射完毕后机动至转载阵地所用时间为：

(6)

转载完毕后机动至第二波次发射点位所用时间为：

(7)

2 约束建立

在第一波次齐射过程中，每个发射点位的使用不得超过一次，即：

(8)

在第一波次齐射完毕后，通过在转载区域转载后到达第二波次发射点位，发射阵地只能使用一次，即：

(9)

第一波次与第二波次发射点位不得重复：

F1⊆F,F2⊆F,F1∩F2=∅

(10)

同一时刻，转载阵地容纳的发射装置数量上限为s，即

(11)

发射装置在转载阵地作业具有先后顺序，每台发射装置转载时间为tz，当第k发射装置正在作业时，第k+s需要等待的时间为：

(12)

式(12)中，s表示转载阵地可以同时作业的发射装置的数量，对于给定的作战对象，s是已知的。参与作战的发射装置总数少于各个待机阵地的发射装置的总数，即

(13)

结合往复式真空泵在运行过程中所产生的温度及其变化情况，基本上超温常常发生在抽空的3阶段中。此时，往复式真空泵进口的真空压力在-0.05～0.075MPa，而出口的压力则处于0.008～0.02MPa。在本组往复式真空泵的实际运行中，其最高的压缩比值等于4.8，而平均的压缩值则为3.04。在抽空2阶段时，该工序所产生的最高压缩比值等于2.16，而其平均的压缩比值则等于1.75。将二者进行比较能够得出，往复式真空泵运行的2个工序中，压缩比之间具有较大的差距，而其所产生的热量则为处于正常状态，发热量与工作时间具有一定的关系。

(14)

(15)

式(13)～式(15)中，S表示发射装置的总数，对于给定的作战对象，S是已知的。

综上所述，构建改进的双层规划模型为：

(16)

3 算法设计

双层规划属于Np-hard问题，而改进的双层规划更加复杂，设计遗传算法，对于解决此类问题具有较好的效果。解决的思路如图2所示。

3.1 Dijkstra算法步骤

Dijkstra算法流程为：

步骤1 初始化，令l(v0)=0，对于v≠v0，令l(v)=∞，S={v0}，i=0。

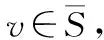
ifl(v)>l(u)+w(u,v)

步骤3 重复步骤2，直到所有出发点在S中，求解Lst。

步骤4 利用Dijkstra算法遍历所有划分点，建立距离矩阵。

3.2 遗传算法设计

改进遗传算法求解最佳的机动路径并进行机动调度，算法流程为：

步骤1 确定染色体配置方案(图3)。将两个波次的打击任务分别定义为第1波次发射编码段，第2波次发射编码段及转载阵地编码段。

步骤2 确定目标函数。对于不同的发射装置，不同的道路情况，求解出所有发射装置的最短机动路径并对其进行机动调度，使机动时间最短；以所有发射装置的最短机动路径及机动时间为适应度函数，通过求解最小适应度值来搜索最优的机动方案。染色体编码如图4所示。

步骤3 算法适应性改造。

1) 随机初始化种群方案。

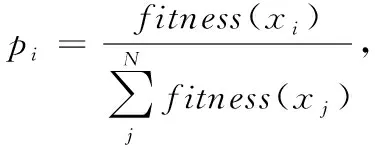
3) 交叉；从种群中随机选择两条染色体进行交叉组合变换，采用实数交叉法，根据交叉概率判断是否交叉，而后随机选择进行交叉操作的两个染色体及交叉位置。针对发射点基因段进行交叉时，首先判断需要交叉的发射点是否与本染色体的发射点基因重复，如果重复，则放弃交叉操作。

4) 变异；从种群中随机选择一个个体进行变异。同理，需要对发射点位进行变异时，首先判断发射点位是否重复，如果重复，则放弃变异。

5) 算法实施；根据遗传算法特点及本问题的特殊性，建立算法实施框架如图5所示。

4 算例分析

对于有2个待机阵地、5个转载阵地、60个发射阵地及62个道路节点的给定路网(如图6所示的具体路网)进行两个波次打击问题的路径规划，其中各个节点分别表示待机阵地(D)、转载阵地(Z)、发射阵地(F)和道路节点(J)，细线表示单行道，粗线表示双行道。

通过Matlab实现遗传算法对最佳机动方案的求解，设置交叉概率为0.3，变异概率为0.1，种群规模为50，迭代次数为 10 000，程序运行收敛情况如图7。

经计算，最佳机动总时间为127.2 h，部分最短机动路径如表1所示。

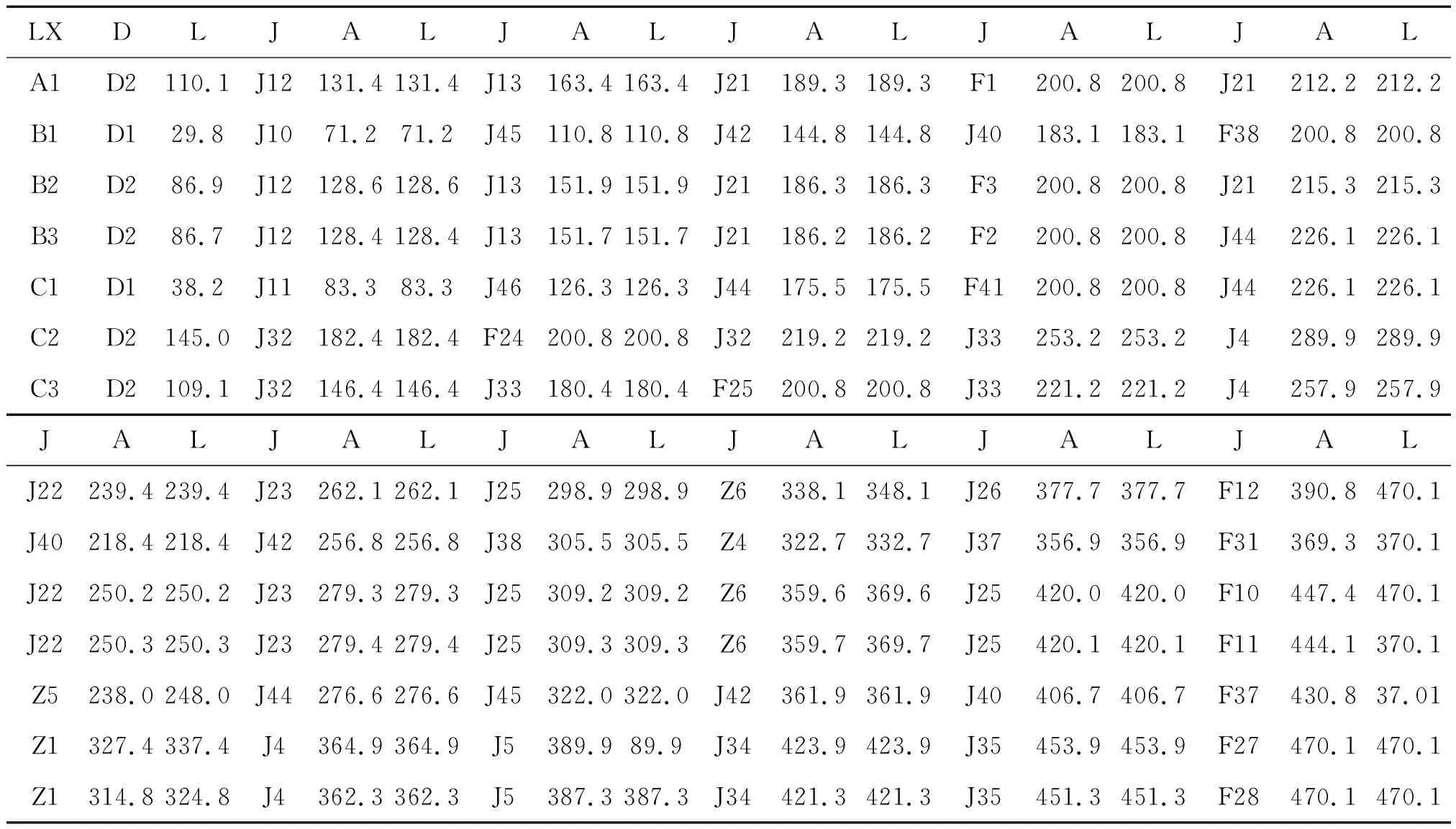
表1 部分最短机动路径

其中，LX表示发射装置类型，D表示待机阵地，J表示道路节点，A表示到达时刻，L表示离开时刻。

5 结论

通过对双层规划模型进行改进，建立了两波次的路径最短、时间最短的双层规划模型，通过改进遗传算法，可以快速找到路径优时间短的最佳机动方案，避免了在直接规划求解时直接通过找到最佳路径然后进行机动调度。调度与路径规划之间没有良好的反馈或是反馈不够全面彻底，可能导致整体机动时间与路径的组合不是最优。文章最后通过算例求解得到了较优的机动方案与机动时间。