基于层权法改进弹道计算中气象数据使用

于佳兴，李 岩，顾 统

(南京理工大学 能源与动力工程学院， 南京 210094)

在现代战场环境下，谁掌握了先机，就掌握了战场的控制权，所以要实现“首发命中”“首群覆盖”，就要考虑各种影响射击精度的因素。在各种因素中，气象条件对射击的影响占比达到70%[1-4]。减少气象因素在弹道解算中的干扰重点在于：(1)提高探测水平，使气象数据更加准确。(2)优化气象因素在弹道解算中的应用方法。对于气象因素在弹道中的应用，存在两个问题：以单一竖直区域概括整个弹道区域气象条件；以准备阶段气象条件当作整个时间段的气象条件。所以要解决测量气象条件与实际气象条件时空不匹配的问题，势必会利用多组气象数据，所以需要改进现有的气象数据的运用方法，使其能适用多组气象数据。一般研究弹道解算中气象诸元对弹道偏差的影响，主要有求差法和微分法[5]。求差法和微分法假设气象只是随高度的变化，没有考虑气象随时间的推移和对空间的覆盖[6-7]。为了探究气象时空变化对弹道的影响，文献[8]根据3日不同气象，分析了3种不同方法的误差，提出了气象时域变化的处理办法，但没有涉及气象涵盖空域的问题。尤其是当通过预测等手段得到了整个区域内的气象数据时，使用单一气象数据的方法并不适用。通过气象预报可得到未来一段时间整个区域的气象条件，也使多组气象数据的运用带来了困难[9-10]。

1 外弹道气象诸元的运用

1.1 近似层权法

近似层权采用真空弹道中各层的相对停留时间作为地炮近似层权[5]。

假设弹箭飞行区域为真空状态，不受气象因素影响，真空弹道顶点Y与全飞行时间的关系：

(1)

计算某一高度为y以上区域的时间时，弹道高度为Y-y，同理时间为

(2)

弹箭通过地面到高度为y的弹道层相对时间为：

(3)

当把弹道层权分为n层时，相对高度si=i/n，si-1=(i-1)/n，所以第i层对整个弹道的权值为

(4)

1.2 准确层权法

将弹道高分为n层使每层弹道与标准气象条件的温差相等，设整体有1 ℃温偏时射程偏差Qτ，求只有第一层无温偏时，射程偏差为X,同理可求得每层射程偏差。即可求出1 ℃温偏在每层中所起作用。公式如下：

Q1=Qτ-ΔX11′

(5)

Q2=ΔX11′-ΔX22′

(6)

某层相对标准气象条件的温度偏差为Δτi，则实际射程偏差为

(7)

每层的层权为

qτi=Qi/Qτ

(8)

1.3 内插法

由于外弹道计算时间步长很小，且每个步长都需要气象数据，而实际测量气象数据一般每两百米采集一次数据，得到的气象数据为一组间隔两百米的点集。考虑到大气系统的连续性，间隔中间某位置的数据一般利用内差法求得。通过对整个气象数据选用样条插值，可得到平滑的曲线。

2 近似层权法在弹道水平方向的运用

通过统计学或数值气象预报手段可得到弹道区域内落点的气象数据，如何使用两组气象数据，需要对现有气象数据的运用方法进行改进。近似层权法在处理气象数据时简便快捷。本文通过推导近似层权法公式产生不同的权值，使其也能适用于水平方向上。

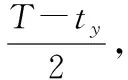
(9)

同理弹道中某一层，上升段或者下降段所用时间占全部时间的层权为

(10)

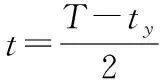
(11)

考虑炮射点和落点气象数据对弹道区域内一点的影响时，可以设置水平权值。对弹道高分2～6层时，每层权值如表1所示，根据竖直权值与水平权值的关系，由表1中2～6层各层的权值，可得到对应的水平各层权值。如表2所示。

该权值反映了弹箭某时刻所在位置气象条件与炮射点和落点气象条件的关系。

根据弹箭飞过的路程占整个路程的比值即可判断起点落点气象对该点影响的大小。弹箭飞行路程占整个路程的权值计算公式如下：

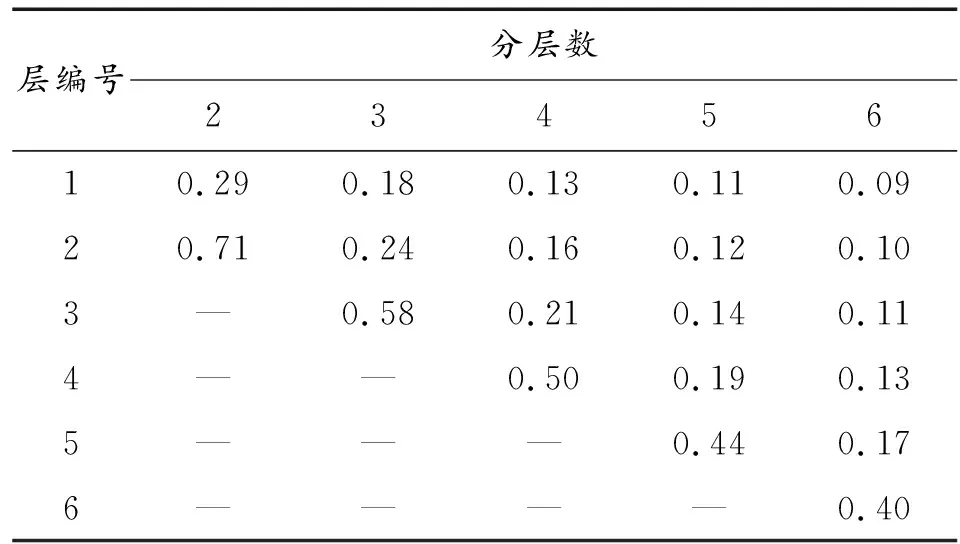
(12)

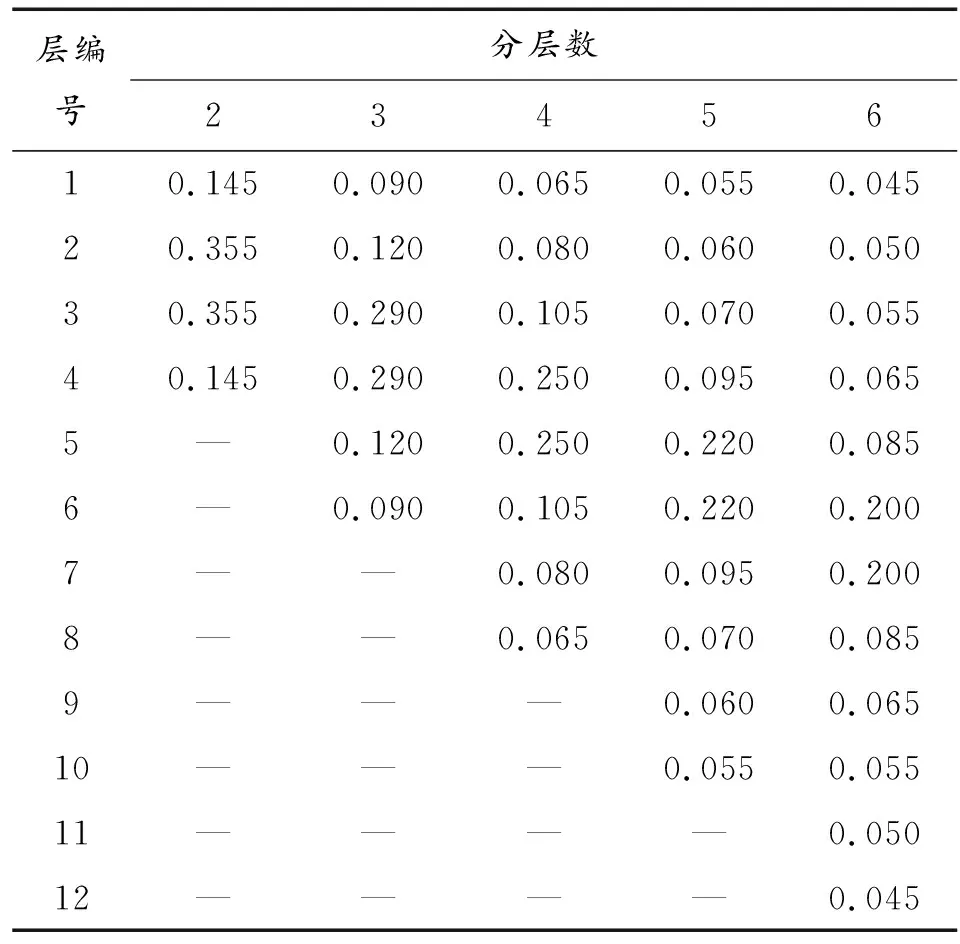
表2 当近似层权分2～6层时对应水平各层权值

弹箭位于弹道区域内某位置的气象诸元为

(13)

e1，e2分别代表起始点和落点气象诸元。

由式(13)可以利用弹道水平面不同的权值，通过炮射点和落点不同地点的气象数据得到弹道区域内不同位置的气象数据。由于水平分层为竖直分层的两倍，应该在近似层权之前，先进行气象数据的处理。

考虑到分层后，该层厚度变小，可利用该层气象数据进行曲线拟合，求积分平均值，作为该层的气象数据代表值。

(14)

式中：ai代表第i层虚温，气压，横风等气象诸元代表值。

利用竖直层权计算各气象诸元的平均值为

(15)

(16)

(17)

(18)

(19)

式中：Wz，Wx，Δz，Δp，Δρ分别为气象诸元平均值，qi为竖直层权，wzi，wxi，Δτi，Δpi，Δρi为气象诸元的偏差量。

3 验证分析

以某型弹50°射角进行弹道仿真，先进行气象数据的处理，将弹道高分为12层，水平方向分为24层，根据炮射点和落点气象数据利用水平权值，计算弹道区域内不同位置的气象，并与处理前每层气象数据对比，如图1、图2、图3所示。计算处理前后各气象诸元相对误差，如表3所示。分别利用处理前后气象数据进行弹道仿真，得到弹道轨迹如图4，图5。计算弹道偏差量如表4所示。

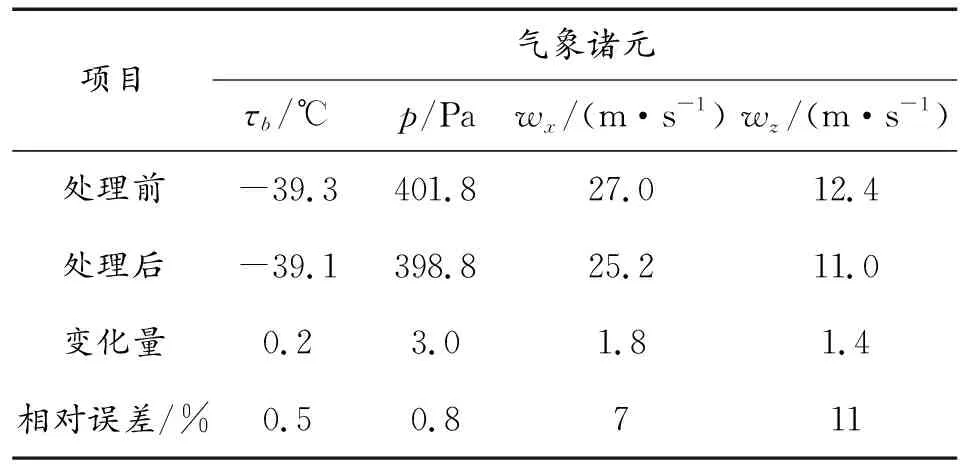
项目气象诸元τb/℃p/Pawx/(m·s-1)wz/(m·s-1)处理前-39.3401.827.012.4处理后-39.1398.825.211.0变化量0.23.01.81.4相对误差/%0.50.8711

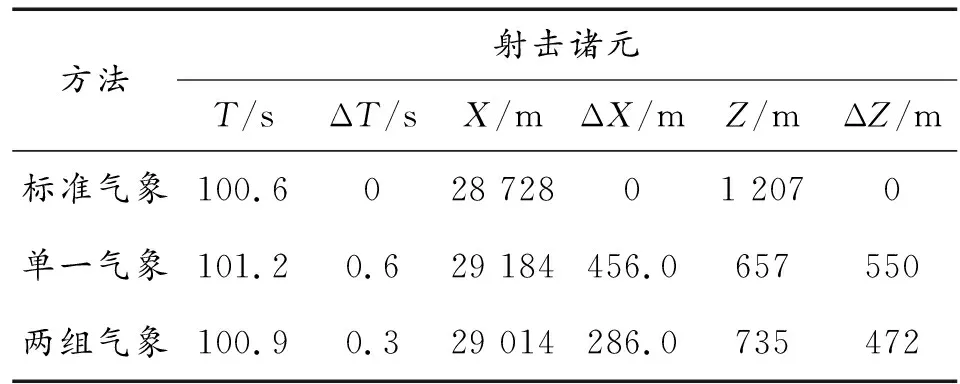
表4 不同方法得到的弹道偏差量

温度、气压在弹道区域内变化较小，分别为0.5%，0.8%。横风侧风变化较大，横风变化了7%，侧风变化了11%。由弹道仿真结果表明飞行时间变化较小。射程的偏差量由456 m缩减为286 m，射程变化量相对减小37%，在侧风的影响下，处理前侧偏为657 m，处理后侧偏为735 m，相对变化6%。

4 结论

本文针对弹道计算中气象条件与实际气象条件不匹配的问题，通过推导近似层权法，提出利用炮射点和落点两组气象插值得到弹道区域内不同位置的气象数据。分别代入弹道方程仿真，对比气象处理前后弹道偏差量，验证了利用近似层权法对弹道水平方向分层可反映弹道区域内气象的变化，可为后续多组气象数据在弹道解算中的应用提供借鉴。