北斗/GPS组合相对定位及精度分析

张成才，岳建平

（1.河海大学地球科学与工程学院，江苏 南京 210098）

目前全球定位系统主要有我国的BDS、美国的GPS、俄罗斯的GLONASS和欧盟的Galileo等。虽然各独立系统的定位精度已经得到了很大提高，使用权限进一步开放，但单系统定位中存在定位精度不足、可见星不多、定位可靠性不强以及受到观测条件影响等问题，有时甚至无法定位解算。为了充分发挥GNSS的综合导航定位优点，扬长避短，将北斗与其他定位系统进行组合定位，获得高精度、高可靠性的用户定位精度具有重要意义[1]。当前我国正加快“互联网+GNSS”的应用建设，探究组合定位成果，这对进一步推动实现跨界融合，包括跨数据融合、跨系统融合等。同时对我国北斗系统的精度验证与进一步应用实现也具有参考意义[2]。

1BDS/GPS组合相对定位数据融合

BDS/GPS组合相对定位中，由于不同系统之间面临的数据精度一致性、数据兼容以及时空基准差异等问题，故在进行定位解算前，需要对不同数据进行预处理（观测数据纯净化），并将文件格式转换成相互兼容的标准化文件（共视文件）。

1.1 周跳探测

周跳可靠探测工作是进行数据预处理的核心环节，在定位数据处理中需要运用有效的方法对其进行探测。本文采用的双频P码伪距观测值来探测周跳（MW组合方法），采用MW组合周跳探测无需了解卫星轨道信息、测站相关信息等，也不需要对测站和卫星间求差。与此同时，还可以完成对数据异常值的探测工作且适用于任意长度的基线解算。

通过任一历元下双频P码伪距观测值P1、P2及载波相位观测值φ1、φ2，即可求得宽巷观测值的整周模糊度：

基于式（1）的观测方程之间进行求差，并简化为：

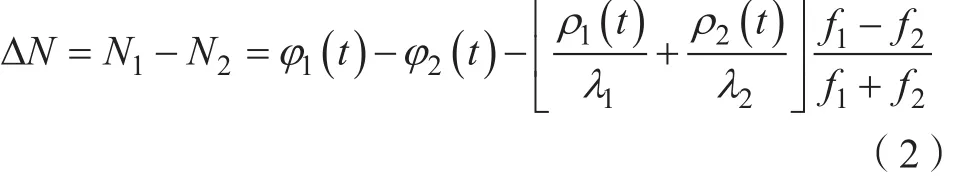
根据从第一个历元到第i个历元所求得的均值及其方差可以推导出迭代公式（3）、（4）：

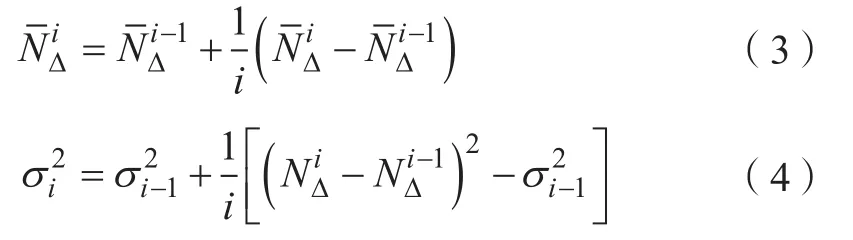
当与之间差的绝对值满足方程式（5）：

则认为第i+1个历元的载波相位观测值中无周跳。通过周跳探测剔除异常值，实现数据的纯净化。

1.2 时空基准统一

1）坐标系统统一。考虑BDS轨道卫星是由MEO＋IGSO＋GEO组成的混合星座，其中MEO和GPS卫星的轨道特征类似，IGSO和GEO卫星的轨道特性与MEO卫星存在不同。相关文献已经证明了GPS卫星的广播星历参数对MEO，IGSO的适用性[4,5]，即MEO、IGSO卫星的轨道计算方法与GPS轨道计算方法类似。对于北斗GEO卫星来说，接近于0°的GEO轨道，GPS卫星广播星历参数并不适用，分析了解北斗GEO广播星历的相关轨道根数特性，采用北斗公布的ICD2.0文件算法实现解算[4]。

GPS和BDS的坐标基准分别采用WGS-84坐标系和CGCS2000坐标系，依靠IERS定义的ITRS坐标框架，两系统的参考椭球基本一致，有着相同的原点、尺度、定向及定向演变的定义[6]。在4个椭球常数中仅f（扁率）有微小差异，α（长半轴）、ω（自转角速度）、GM（地心引力常数）相同。在精度要求不高的情况下，不需要考虑系统之间的坐标转换，而对于高精度定位服务要求的用户，可以考虑用七参数布尔萨（Bursa）转换模型来解决这一问题，其公式：

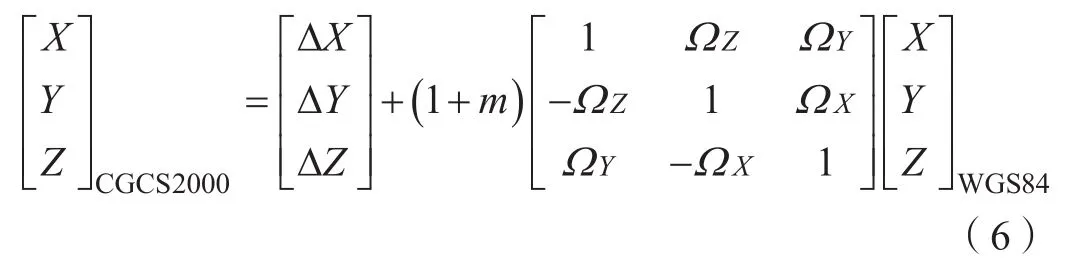
式中，∆x、∆y、∆z为坐标原点经平移引起的3个平移参数；Ωx、Ωy、Ωz为坐标旋转引起的3个旋转参数；m为尺度变化参数。

2）时间系统统一。高速运行的高空观测目标，要描述其精确位置就必须提供相应的精确时间。GPS时（GPST）与北斗时（BDT）同属于原子时间系统，均无闰秒。但GPST与国际原子时（ATI）具有不同的起点，相差19 s，GPST 与UTC之间的差异为秒的整倍数，其后随着跳秒的增加而增大。BDT的原点为2006-01-01 12:00时的UTC时刻，其与UTC的偏差保持在1 μs以内。这两个系统除原点相差1 356周外，BDT与GPST还相差14 s[6]。当进行GPS/BDS组合定位时，BDT/GPST需统一到同一时间系统下。

2BDS/GPS组合相对定位数学模型

基线解算中，先就非差观测方程进行分析：

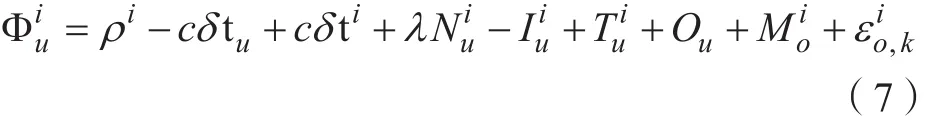
式中，为k波段下的观测噪声以及的卫星轨道计算误差。

通过式（7）载波相位观测方程描述，对接收机（u和r）与可视卫星（i和j）之间分别求取一次差分得到双差观测值以提高定位精度。对于中长基线高精度的数据处理方法，一般采用无电离层组合解算。在相对定位中，双差观测值可表达为：

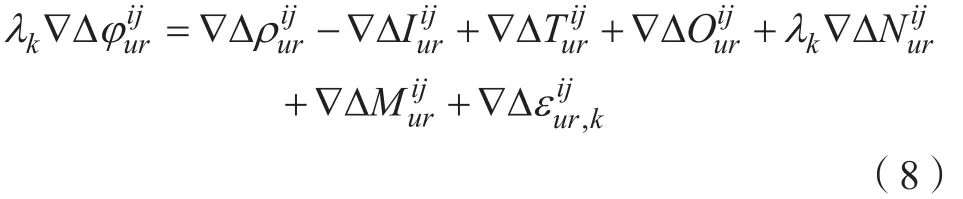
根据无电离层组合系数对式（8）式进行组合，可推导出下面的式子：

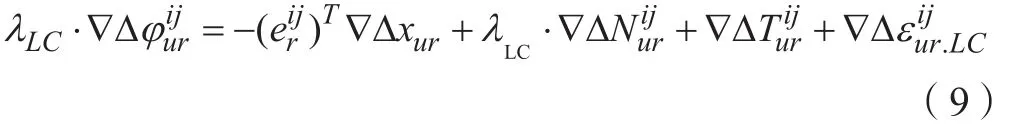
将无电离层组合的双差整周模糊度项分解为基频L1模糊度和宽巷模糊度组合形式：

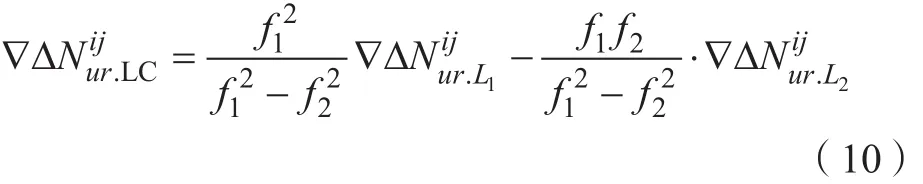
整合式（9）、（10）得到LC观测方程如下：

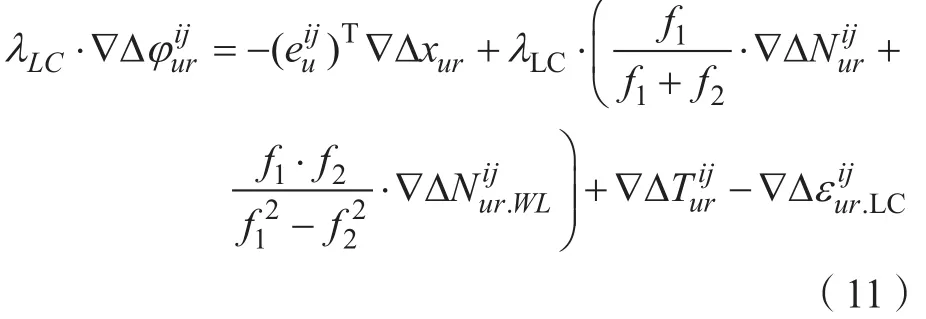
双系统组合定位需要考虑融合问题，但BDS与GPS解算原理一致，则双系统对应的误差方程表达形式为：

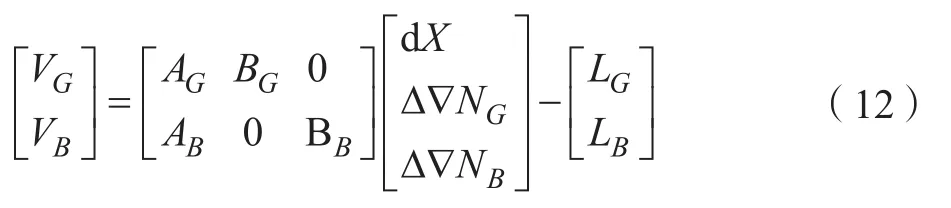
式中，L为常数项向量，A和B分别为坐标改正数dX和双差整周模糊度∆∇N的系数矩阵。

3 实例分析

双系统组合定位采用载波相位观测值建立函数方程进行高精度定位解算，其实质就是对双系统接收设备所接收的卫星载波信号以及来自不同系统卫星的导航电文进行综合数据处理，从而用以确定卫星与用户之间以及用户与用户之间的相对位置。

在基线边两点坐标是精确已知的条件下，从卫星可用性分析以及定位精度等多方面分析BDS/GPS组合定位的性能。数据采用2016-12-10 6:00～8:00的观测数据，见表1。

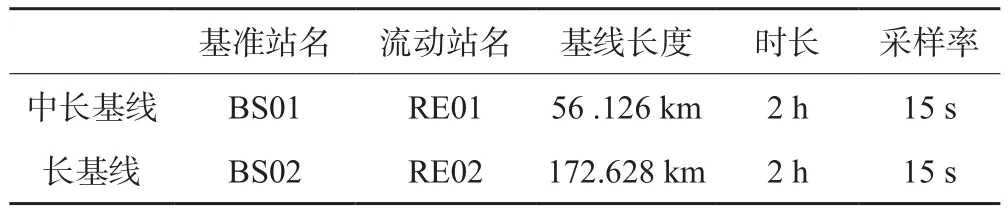
表1 同步观测数据

1）定位卫星可用性研究。考虑到组合系统静态相对定位，可视卫星的几何分布强度是获得高精度定位结果的重要因素之一。PDOP值（可视卫星位置精度）是衡量卫星定位精度的重要指标。本文通过对同步观测的中长基线、长基线的一个单站卫星的个数和PDOP值求解，进行卫星可用性研究。如图1（卫星个数）、图2所示（PDOP值）。

分析图2的PDOP值可知，组合系统在当前观测条件下PDOP值要小于单个系统的值，而且稳定性好。但BDS、GPS单系统的PDOP与组合系统相差不是很大且小于2.5，对于定位精度和稳定性判定还需要进一步分析，不妨预测BDS/GPS双系统定位的精度要好于单系统。

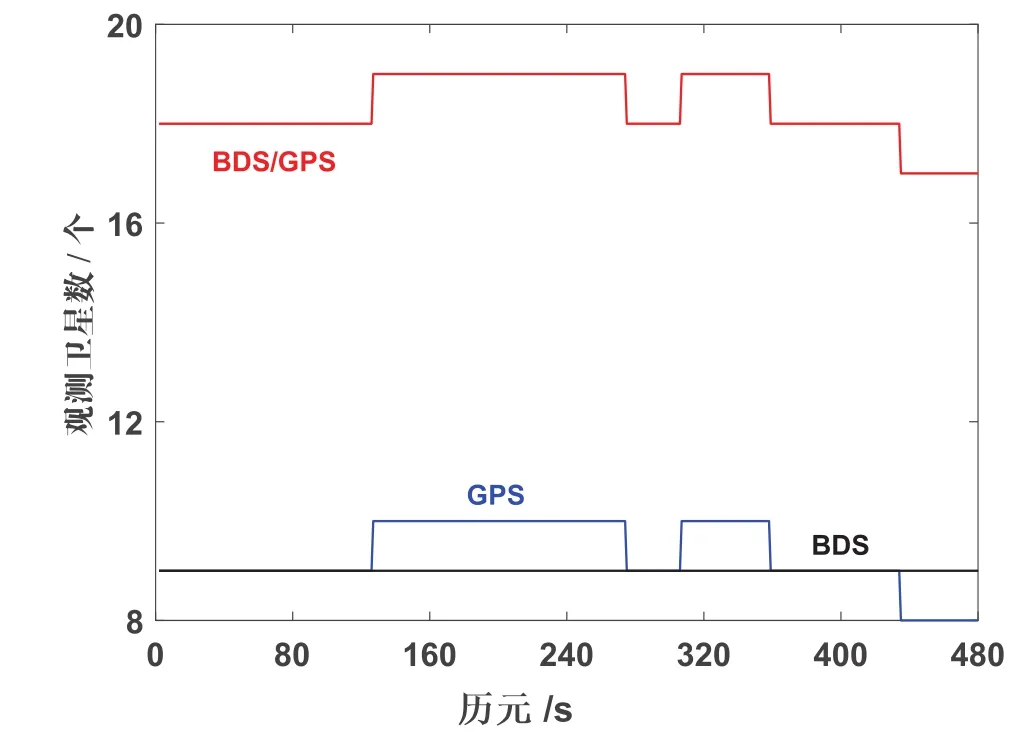
图1 单站卫星个数

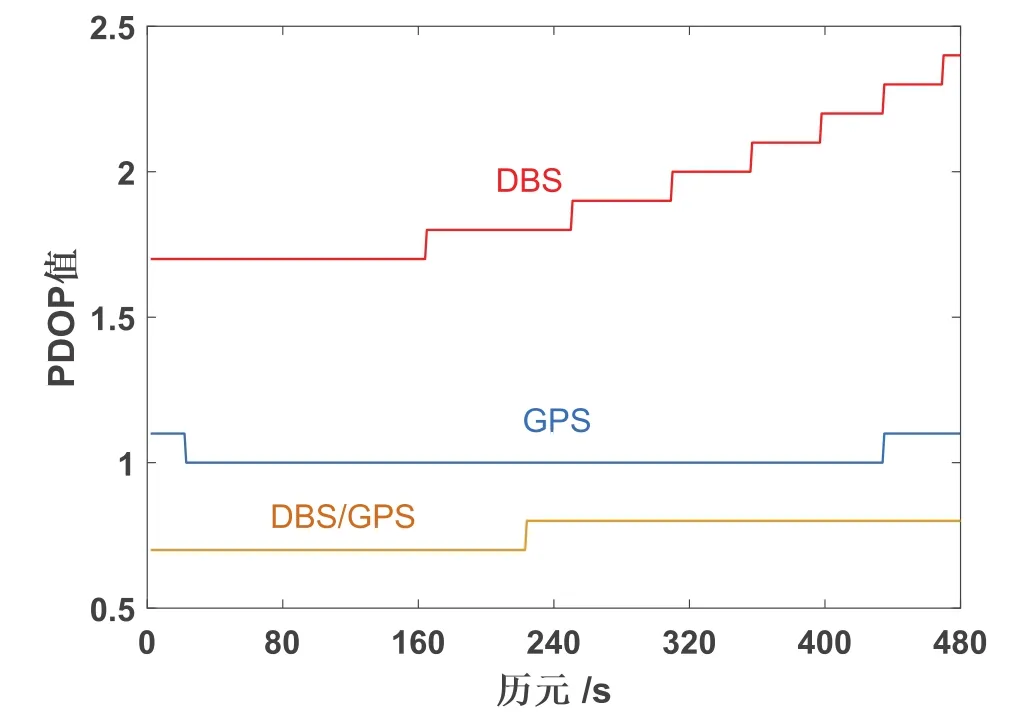
图2 单站PDOP值

2）定位精度分析。在整周模糊度求解过程中，可视卫星空间位置影响模糊度精确固定。可视卫星高度角越大，所受到的误差影响越小，模糊度固定越快。本文采集同步观测数据，卫星截止高度角为15°，采用最小二乘模糊度降相关平差法（LAMBDA法）可以缩小搜索范围，加快搜索进程。卫星空间位置情况如图3、4所示。就图3、4来看，当前时段下BDS卫星高度角变化较GPS缓和，高度角均大于15°，接收机保持了对所有卫星的连续观测。而GPS可视卫星情况较BDS差，接收机无法保持对卫星的连续跟踪观测，相比BDS，所受误差要大、模糊度固定困难，故预测定位精度与可靠性没有BDS好。

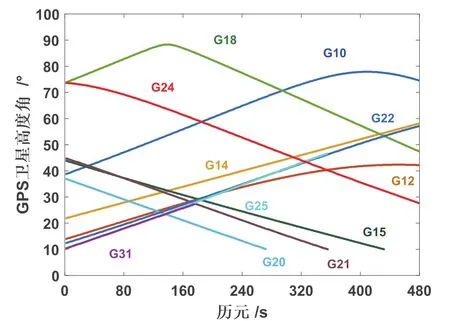
图3 单站GPS卫星高度角

图4 单站BDS卫星高度角

在模糊度精确固定前提下，对BDS、GPS、BDS/GPS组合数据进行位置求解并与已知真值求差，得到基线在E、N、U3个方向的坐标差值，进而对双系统相对定位误差序列和均方根误差（Root Mean Square，RMS）进行分析，如图5（中长基线）、6（长基线）所示。

对图5、6中E、N、U3个方向的误差序列分析可知，BDS/GPS组合定位的精度在中长基线下优于单一系统。但北斗的定位精度和稳定性较GPS更好，特别是长基线下N方向和U方向，定位效果尤为明显。本文还分别计算出均方根误差（RMS）用以定量分析其定位精度。通过PDOP值来看，北斗卫星的整体空间几何结构的确不如GPS。但从表2中可以看出，GPS在长基线下定位精度要稍逊于北斗系统，在中长基线下定位精度与GPS相当。由于存在的各种可能问题，采用BDS/GPS组合的定位方式较单系统精度并没有明显优势，反而北斗系统在3个方向上的定位精度较好。通过一系列数据分析来看，基本与前面的预测相吻合。

图5 中长基线3种组合方式E、N、U分量误差

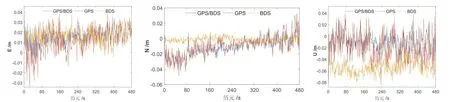
图6 长基线3种组合方式E、N、U分量误差

表2 不同系统相对定位RMS值/m

4 结 语

在同步测量环境下，可见卫星数时刻发生变化。BDS/GPS组合系统可见卫星数和DOP值比单系统有所提高，空间卫星的几何分布强度得到有效的改善。当前我国北斗系统尚在建设完善当中，定位卫星分布不均匀，导致卫星的空间几何结构强度不如GPS。从本文的算例来看，中长基线情况下，北斗系统精密可达毫米级，较GPS系统要好，可满足高精度导航定位服务需求分析。在长基线下，组合定位系统较单系统有所提升，且稳定性较好。可以预见的是，当北斗系统建设完成后，定位精度和GPS大致相当，甚至在某些地区要比GPS精度高，可靠性更好。