地面三维激光扫描点云质量评价技术研究与展望
2018-08-29花向红赵不钒陈西江
花向红,赵不钒,陈西江,宣 伟
(1.武汉大学测绘学院,湖北 武汉 430079 ;2. 武汉理工大学资源与环境工程学院, 湖北 武汉430072;3.武汉理工大学土木工程与建筑学院, 湖北 武汉430072;4.武汉大学灾害监测和防治研究中心,湖北 武汉430079)
地面三维激光扫描技术(Terrestrial Laser Scanning,TLS)是上世纪90年代发展起来的一种快速获取三维空间信息的技术手段,该技术通过非接触式扫描的方式获取目标物表面信息,包括目标物的点位信息,以及目标物的距离、方位角、天顶距和反射率等。每秒扫描数据可高达上百万,所获数据为离散的点云形式,称为点云数据。对点云数据进行处理,可实现对扫描目标的三维重建以及其他多种应用功能。利用激光点云产品之前需要准确确定点云数据的精度和可靠性,而点云质量包含点云数据精度和点云模型精度,正因为如此,对点云数据及点云模型质量进行评价才显得尤为重要。三维激光扫描技术与传统技术不同之处在于获取的是目标物的大量点云,无法确定对应点在目标物上的具体位置,采用传统的点位精度评定方法有一定的局限性。自从三维激光扫描开始应用于测量领域,国内外学者和工程技术人员对点云数据质量进行了大量研究,主要集中在点云误差来源、点云空间分辨率、点位精度、点云误差空间、配准精度、简化精度、三维建模精度等方面,并取得了一定的成果。本文主要介绍了地面三维激光扫描点云质量评价技术研究成果,并对地面三维激光扫描点云质量评价发展趋势进行了展望。
1 点云质量评价
点云质量评价包括点云数据质量和点云产品质量评价,点云数据质量评价主要是根据离散点自身误差所建立的点云误差空间模型,再由点云误差空间模型推算点云标准差;点云产品质量评价主要是研究点云所构成模型的精确度,包括点云模型与目标物的契合度、属性信息的精确度等。
1.1 点云数据误差来源及自检校模型
地面三维激光扫描的误差源是评价扫描点云数据质量和扫描仪性能的基础。地面三维激光扫描仪的误差源多种多样,按照误差产生的原因分为5类[1]:地面激光扫描仪的仪器误差、扫描物体表面特性引起的误差、环境因素引起的误差、数据采集方法以及点云数据处理过程中产生的误差。其中,地面激光扫描仪的仪器误差主要由其内部的激光测距仪、激光偏转单元等部件引起,可以分为测距误差、激光偏转单元与测角误差以及轴系误差3个方面。扫描物体表面特性引起的误差直接影响激光测距结果,激光测距精度主要受目标物体表面的粗糙程度、物体的材质和颜色、物体的温度和湿度、激光入射角等因素影响。不同材质的物体表面,激光的反射率与渗透作用不同,进而导致接收到的返回激光信号强度不同,直接影响测距精度。环境因素引起的误差主要由周围环境的温度、相对湿度、气压、光照条件、周边的辐射干扰、架设扫描仪的地面的不稳定性等引起,温度、相对湿度和气压主要是影响激光信号在大气中的传播速度和传播路径,而光照条件影响目标物体的反射率。
在国外,Lichti对扫描仪测量误差进行了系统研究,给出地面三维激光扫描仪的角分辨率与扫描间隔、扫描仪量化精度和光斑直径的关系。点云空间分辨率分为角度分辨率和距离分辨率,角度分辨率决定了目标细节的提取能力。角度分辨率受光斑大小、扫描间隔和量化精度共同影响,提出了角度分辨率的平均调制传递函数模型和有效瞬间视场角模型;国内学者施贵刚[1]等分析了点云数据获取过程中的误差来源及其对扫描精度的影响。
地面激光扫描仪自身的误差大多属于系统误差,是影响点云数据质量的重要因素,因此需要通过精密检修以及检校来减弱或消除影响。目前,地面激光扫描仪的检校主要分为单项检校法和自检校法两种方式。单项检校法是指按照仪器的组成部件,如激光测距系统与角度测量系统分别进行检校[2-4],这种检校方法需要建立检校场。
自检校法可以将扫描设备所有系统误差看作一个整体,通过外部已知条件同时求解所有系统误差以及其他系统参数。运用自检校法进行扫描仪的系统误差检校已经越来越普遍。Bae等在假设扫描测角测距系统与全站仪类似情况下,将扫描仪的测距系统误差分成8种,水平测角系统误差分成7种,竖直测角系统误差分成4种,提出了扫描仪系统误差自校正模型,并采用数值模拟法和室内标靶自校正实验计算了Faro880扫描仪的系统误差。Rietdorf 等(2004)利用全站仪的误差模型,提出了基于刚体变换的扫描仪自检校模型的概念。官云兰等(2014)利用全站仪系统误差的模型对扫描仪的系统误差进行研究,详细阐述了基于刚体变换的系统误差自检校方法,通过对扫描坐标进行系统误差改正提高了点位精度。Lichti[5](2010)对各种自校正模型进行了综述,并将目前的自校正模型分为基于平面的自校正模型和基于标靶点的自校正模型两种,给出了两种参数约束条件。其后,一些学者围绕这两种检校方法展开了地面激光扫描仪的系统误差检校工作。Chan 等(2015) 提出了一种基于圆柱特征的地面激光扫描仪自检校模型,从实验结果中可以看出,该自检校方法能够从一定程度上减弱检校参数之间的相关性。宣伟等(2016)根据Lichti[6](2011)模型提出,检校参数之间的相关性及其自身的显著性是影响自检校法结果可靠性的直接因素,提出了基于参数自动优化的地面激光扫描系统误差自检校方法,建立了基于21个附加参数的系统误差参数模型,推导了基于靶标点的自检校法计算公式,针对解算参数之间的相关性与显著性,提出了参数自动优化方案,得到了相关性低、显著性高的最优参数组合,最大程度上消除了系统误差对点云数据质量的影响。
1.2 点位误差模型
对于激光点位误差(或点位精度),目前主要是根据仪器厂商所提供的性能指标,根据测距、测角与激光点位的关系,利用误差传播规律得到激光点位误差模型,从而判断点云数据质量。根据学者研究,激光点位误差主要由两部分组成,一部分为由激光扫描仪本身测距、测角机理所产生的点位精度Dρθφ-xyz;另一部分则是由激光发散性所产生的基于光斑影响的点位精度Dspot-xyz[7]。
1.2.1 测距测角引起的点位误差Dρθφ-xyz
根据三维激光扫描原理,地面激光扫描仪的原始观测值为距离观测值φ、水平角观测值φ及垂直角观测值θ,假设在某一扫描仪坐标系下的任一激光扫描目标点坐标为X=[x y z]T,则激光点位Xin与测距、测角之间的关系为[8]:

激光点位Xin理论情况下服从正态分布,根据误差传播规律可得到激光点位Xin的协方差矩阵:

Cinst中的测距精度是在入射角为0情况下的结果,而实际扫描过程中,激光波束与扫描目标基本不垂直,因此需要考虑入射角对测距精度的影响。Darion Grant(2012)[9]考虑了入射角对测距精度的影响,假设入射角为α,则其测距精度为从而测角、测距协方差变为:

由文献(Sylvie Soudarissanane,2011)[10]可知,入射角α可以表示为激光束向量与任一点激光点位法向量的形式:

式中,→为激光束向量,为任一点法向量。
由式(2)可得到激光点位坐标Xin的协方差为:


1.2.2 光斑影响下的点位误差Dspot-xyz
光斑对点位精度影响的前提是光斑大小的计算,光斑大小由激光波束宽度决定,是激光点位不确定性的范围。关于光斑大小的计算方法有很多种,陈西江[11]等(2015)研究了同时考虑入射角和发散角的广义情况下光斑大小计算模型,利用扫描间隔对相邻光斑大小的影响计算了平均光斑大小。给出了发散角和入射角影响下服从不同分布函数的光斑大小点扩散函数,依据光斑大小点扩散函数,计算了激光点位在光斑水平和垂直方向的标准差,得到基于光斑影响的点位精度。
根据激光系统特性,对于脉冲式激光扫描仪,脉冲中的能量沿着光斑中心不是均匀的,是近似地服从对称的高斯分布(正态分布),因此在确定激光点位与光斑关系时,在同时考虑入射角α和发散角β的情况下,其协方差矩阵如式(6)所示:

1.3 点位误差空间模型
点位误差空间表示的是激光点位在某个区间内的不确定性。不确定性是客观世界或现象本身的不精确性、随机性和模糊性,包括位置不确定性、时域不确定性和空间数据不完整性等。激光点位不确定性的研究集中于空间位置的不确定性[12]。三维激光点云数据质量由三维方向的点位误差空间决定,误差椭圆分析的是目标平面上的误差区间,因此,可以基于误差椭球方法表达激光点位误差空间,基于误差椭球表达的激光点位误差空间由于需要确定椭球缩放系数,造成了其表示的误差空间的不确定性[13]。
1.3.1 利用点云误差椭球评价点云精度
在激光点位服从正态分布的情况下,点位误差空间一般用误差椭球来表示。由点位误差空间模型可知,三维激光点位已经演变为误差椭球形式,根据正交矩阵理论,将误差椭球形式化为标准椭球形式[14]。

式中,椭球半轴长度为a=kλ1;b=kλ2;c=kλ3;k为误差椭球缩放系数,、和分别为C矩阵的X特征值。
根据公式(7)表示的误差椭球标准形式,可得到激光点位概率密度函数为:

则激光点位落入误差椭球G′内的概率为:

代入式(9),得到点位概率为:

利用球坐标积分形式将式(10)化为:
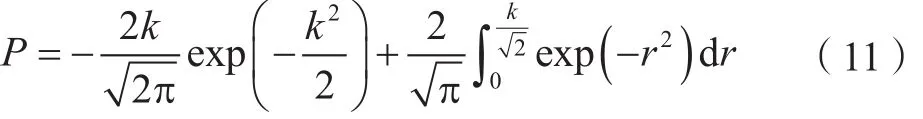
根据式(11)即可计算激光点位落入误差椭球内的概率;k为误差椭球的缩放因子,选取不同的k值计算得到对应的概率值,结果如图1所示。

图1 缩放因子k与激光点位落入误差椭球内的概率
由图1可以看出,不同的缩放因子k对应着不同的点位概率,k的选值决定了激光点位落入误差椭球内的概率。因此,在实际计算点位误差椭球时,需要根据要求选取合适的缩放因子。一般情况下,选取k=2,产生一个概率为73.85%的误差椭球;当k=3时,激光点位落入误差椭球内的概率已经高达97.07%,该误差椭球基本上包含了所有的误差信息,因此将k=3对应的误差椭球作为极限误差椭球[15]。
在考虑相邻点位误差椭球相互影响的情况下,扫描间隔对点云误差椭球的影响较大。在相邻误差椭球存在交集的情况下,根据相邻误差椭球公式,可以计算相邻误差椭球交集体积,从而得到相邻误差椭球体积,计算平均点位误差椭球,从而消除了相邻点位误差椭球重合度的影响。再由误差椭球与点位中误差的关系确定点云精度,即实现了利用误差椭球对点云精度的评价[16]。该评价指标真实地反映了点云精度的好坏,为不同设备获取的点云进行精度对比分析提供了有力的计算模型,同时可以实时地监测到扫描点云任意地方的精度状况,为用户采取合适的扫描方式提供了理论基础。
1.3.2 利用误差熵评价点云精度
在激光点位分布不服从正态分布的情况下,无法采用误差椭球来评价点位误差,部分学者将信息论中的信息熵与误差熵引入到三维点位误差空间评价中。误差熵这一概念由信息熵推广而来,即对激光点位椭球模型的广义信息熵进行极坐标积分,从而得到广义的误差熵模型。陈西江[17](2014)推导了激光点位误差熵模型,广义n元P-范分布的信息熵为:

当P=1时,P-范分布退化为拉普拉斯分布,其信息熵为:

当P=2时,P-范分布演变为正态分布,其信息熵为:

令DX的特征值为,则式(14)为:

n元P-范分布函数下的误差熵为:

由式(16)得到n元P-范分布的误差熵与激光点位误差椭球的关系:

式(17)建立起了n元P-范分布误差熵与点位误差空间之间的关系。
根据对激光点位误差分布进行统计分析可知,激光点位服从的是P=1.7的P-范分布。利用误差熵对激光点位精度进行分析方法,可以间接地将点位误差转为误差椭球的形式,当n=3,P=1.7时,式(17)误差熵转化为近似误差椭球形式,如式(18)所示:

根据式(18)计算每个激光点位的误差熵,该误差熵表示的误差空间如图2所示。

图2 误差熵(k=2.388)
计算误差熵对应点云误差椭球的实际体积,得到点云误差空间,并根据点云实际误差椭球体积计算每个激光点位的平均误差空间,从而得到对点云及点位精度的评定。实验结果表明,用该方法可以实现不同分布状况下点云及点位误差空间的评定,为点云数据质量的评价提供了基础。
1.3.3 工程应用
宣伟[18]等(2016)从测距测角误差以及光斑大小出发,基于误差椭球理论,建立了激光点位误差空间模型,考虑了点云数据中相邻点位误差空间之间的交集,得到了点云实际误差空间与点位实际误差空间,根据两者的关系,确定了点云变形可监测性指标,来区分点云误差与真实的变形量。将该方法用于武汉二七长江大桥主塔变形监测中,检验其可行性。其变形提取的结果见表1。其中,2014年9月第一次扫描的桥塔点云数据作为变形计算的参考点云,周期1是指2014年11月相对于2014年9月;周期2是指2015年1月相对于2014年9月。x方向是指水流方向;y方向是指桥体方向;z方向是指铅垂方向。表2给出了沿着x、y、z方向的变形可监测性指标DMI计算结果。为了更直观地分析变形计算的结果,计算QF值,结果如图3所示。

表1 桥塔上3个区域的变形参数(Δx,Δy,Δz)/mm

表2 沿着x, y, z 方向的变形可监测性指标计算结果/mm

图3 桥塔上3个区域的Quality factor (QF)结果
由图3、表1、表2可以看出,3个监测区域在z方向都不存在任何明显的位移,即未出现任何明显的沉降。对于塔身区域在水平方向上也存在一定的位移,而塔顶区域在监测期间在水平方向上存在位移的情况,可能是温度和风力导致桥塔出现了摆动所致。
1.4 点云配准质量评价
三维激光扫描的过程中,由于物体的遮挡、扫描仪的限制等原因,要完成对一个物体的完整三维数据获取,地面三维激光扫描仪需要多测站多角度进行扫描。而每站扫描获得的点云坐标为扫描仪中的坐标系,需要将多测站多角度的点云配准到全局坐标系下。由于仪器本身的原因、 设站位置的差异以及外界条件的影响,都会使配准产生误差,而且点云配准过程中误差会传递。同时,为了满足工程需要,应将扫描的点云配准到工程坐标系统中,也涉及到点云全局坐标系统配准到工程坐标系统的误差传递。目前,点云配准主要有标靶配准和无标靶配准两种方式。
程效军[19](2009)研究了点云配准误差传播的规律,按照摄影测量影像匹配的原理,对地面激光扫描仪采集的点云数据进行配准,根据间接平差、协因数传播原理以及协方差传播定律得出了多站配准点云误差传播的数据模型及其计算方法。通过实验,验证了点云配准精度与点云模型累积误差的定量关系,实现了点云配准精度的评估。
施贵刚[20](2009)针对六参数表示的点云配准模型,利用误差传播定律,推导出了基于六参数的点云配准误差传播模型;杨荣华(2011)在分析了点云四元数配准模型的基础上,利用矩阵微分性质和误差传播定理,推出了基于四元数配准模型的误差评价模型,同时还推导出观测值精度和平移参数精度已知情况下的四元数求解精度计算公式。
1.5 点云简化质量评价
点云简化后质量评价主要从简化精度、简化率、简化速度3个方面来衡量。简化精度即精简后的点云数据所表达的曲面与原始点云数据所表达的曲面之间的误差,因此要保证误差在可接受范围内,并且尽可能多地保留原始点云数据中的特征信息。简化率即精简后的点数相对于原始点数的百分比,反映了点云数据简化的力度,应在保证简化精度的前提下,尽可能减少数据点数。在实际操作中,为了保证后续模型重建的质量,需要选择合适的简化率。简化速度即在保证精度和简化率的前提下追求更高的效率和更快的速度。
目前,点云简化精度的评价一般是通过简化前后图像的对比分析实现的,评价结果具有较大的主观性,缺乏定量的评价分析。考虑到点云简化过程中保留的几何特征信息的多少会直接影响到最终点云模型重建的质量,因此,点云简化精度的评价还可以转化为精简后的点云数据所包含特征信息的量化问题。武剑洁(2004)通过熵理论来描述局部点云的特征信息,利用局部熵突变发生在曲面形状变化剧烈区域的特性,描述采样点所包含的局部特征信息量,如果是基于点法向量的概率密度函数计算的熵值,则熵值越小,说明该点所在的邻近区域法向量近似相同,该点所在的局部区域无序程度越高;反之,熵值越大,该点所在的局部区域无序程度越低,即熵值的大小能够直接反映局部曲面的变化状况。简化后任意点的信息熵为:

式中,θi表示点i的法向量夹角;θj表示点i邻近点j的法向量夹角;pi与pj分别点i及j的法向量夹角的概率分布。点云平均熵为:

简化后,熵值越大,说明平面保留的点较多,特征表面变化明显区域保留的点较少;熵值越小,说明平面保留的点较少,特征表面变化明显区域保留的点较多;平均熵越小,特征表面变化明显区域的点越多,对扫描物体的描述越精确。
1.6 点云产品质量评价
点云产品质量直接关系到点云产品应用的可靠性,对点云产品质量进行准确评价显得尤为重要,而点云产品主要是点云所构建的三维模型,因此,对点云模型质量的评价就可直接反映点云产品质量的评价。目前,对点云三维模型质量评价的主要方法有主观评价方法和客观评价方法[21]。而主观评价方法主要依靠人的肉眼观测对模型表面粗糙度进行评价。该评价方法简单直观,但需要耗费大量的人力和时间,并且受观测者个人因素的影响较大,降低了点云产品评价的公平性和准确性。而客观评价方法主要是依靠所构建的数学模型进行评价,该方法可以避免人的主观判断对评价造成精度缺失的影响,有效提高点云模型评价的准确度和效率。
点云产品形式很多,包括建筑物点云模型、工业产品模型如文物点云模型等。 不同的点云产品形式,其质量评价方式也不相同。 针对建筑物点云模型,可以根据建筑物表面特性评价点云模型精度,如Acka 等利用三维表面匹配来评定建筑模型的点云质量。三维表面匹配可以估计建筑点云与验证点云之间的欧氏距离,而该欧氏距离与点云数据获取方法无关,通过该距离可以确定三维模型的质量,同时解决了参考系统精度、点位精度及数据完整性问题,可以作为建筑物点云数据质量的评定方法。
由于工业产品表面并不是完全规则的,无法根据表面特性来实现点云模型精度的评价。针对此,首先可以通过计算工业三维模型表面的高斯曲率、截面曲率、斜率、双向曲率、法向矢量等,实现工业产品局部曲面质量的评价。其次,根据工业产品表面整体几何尺寸、面积或几何特征间的约束关系,如通过计算工业产品孔、槽之间的尺寸和定位关系,实现工业产品三维模型整体精度的评价。
以上方法主要是通过利用所构建的点云模型进行直接的质量评价,由于构建点云模型的方法不同,因此,根据不同点云模型构建方法及实现的不同点云模型产品,实现对点云模型精度的评价,如点云模型构建方法主要有显式和隐式方法,显式方法主要是基于原始点云进行三角网的构建,通过该方法构建点云模型的精度评价,主要是根据点位误差和误差熵之间的关系[22]构建三角网中点与点之间的线元误差熵[23],并最终实现三角网误差熵模型的构建,利用该模型可以实现对点云显式模型的精度评价。而隐式方法主要是在原始点云数据基础上进行内插,然后通过密集点云的三角网重建实现点云模型重建。
2 展 望
地面三维激光扫描技术目前已经被广泛应用于文化遗产保护、考古、滑坡监测等领域,该技术应用的关键是获得物体表面的大量点云数据,而在广泛应用过程中主要关注前期的数据处理,包括点云配准、点云简化、点云去噪、点云分割、三维建模及纹理映射等几个方面。通过前期的点云数据处理,获得用户所需要的各类点云产品,如目标物特征信息、目标物分类信息、滑坡变化信息、工业、厂房及各种建筑文物设施的三维模型等。在获取点云产品后,很少对其应用的可靠性进行准确评价,即点云数据和点云模型的质量评价是点云产品得以有效和准确应用的基础和保障,它是测绘及其他行业研究的一个重要内容。点云质量评价是一个系统工程,涉及到点云数据精度和点云模型精度模型的构建,由于点云不是单一的点,因此,点云数据精度将会更多地考虑相邻点误差相互影响后所形成的点云误差模型。而点云模型精度将会根据不同的模型构建方法,运用不同的精度评价方法实现点云模型精度的评价,最终形成自适应评价体系。同时,点云模型是非离散数据格式,在对点云模型精度评价的过程中,将会引入新的评价模型,如曲面光滑度、粗糙度等模型来实现点云模型局部和整体精度的准确评价。在实现点云数据和点云模型精度评价体系构建后,才能真正实现地面三维激光扫描应用可靠性的普及,充分发挥地面三维激光扫描技术的优势。
