风力机智能叶片气弹建模与主动控制仿真研究
2018-08-29张文广刘瑞杰王奕枫
张文广, 刘瑞杰, 王奕枫
(1.华北电力大学 新能源电力系统国家重点实验室,北京 102206; 2.华北电力大学 工业过程测控新技术与系统北京市重点实验室,北京 102206)
近年来,随着全球风电的快速发展,为降低发电成本,风力机的额定功率越来越大,叶片长度也随之增加,其结构更具柔性。叶片作为风力机的主要承载部件,增大叶片尺寸会使其处于更为复杂的气动环境,导致叶片形变更为剧烈,其受到的疲劳载荷和极限载荷也不断增大。这对大型风力机叶片的设计和控制提出越来越高的要求。变桨控制作为目前风力机唯一的主动控制方法,由于调节速度较慢等问题难以满足风力机大型化的需求。近年来兴起的智能叶片技术,包括尾缘襟翼技术、微插片技术和主动扭转技术等可有效地克服这些难题[1]。其中,尾缘襟翼技术可通过改变叶片翼型形状来改变叶片的气动特性,进而减小叶片剧烈形变和所受疲劳载荷[2]。目前,国内外对智能叶片的研究主要在理论和实验研究阶段[1-2]。为进一步研究尾缘襟翼对智能叶片叶尖偏移量及降载控制的作用,有必要对带有尾缘襟翼的智能叶片进行气弹建模与控制。
Staino等[3]建立了不考虑重力和惯性载荷的摆振方向气弹模型,并研究了线性二次型(LQ)控制对摆振方向叶尖偏移量及频谱的影响。Castaignet等[4]建立了不考虑重力影响的挥舞方向的气弹模型,并研究了尾缘襟翼对挥舞方向叶根弯矩的影响。Ju等[5]建立了不考虑耗散能的挥舞方向气弹模型,并研究了输入整形控制对挥舞方向叶尖偏移量的影响。Chen等[6]建立了风力机叶片摆振方向的弹性模型,并采用模糊控制通过阻尼器对叶片的摆振方向偏移量和基层剪力进行了控制。刘翀等[7]建立了叶片气动模型,研究了桨距控制对风力机气动性能的影响。徐燕等[8]建立了不考虑重力作用的叶片挥舞气弹模型,并研究了基于极点配置的比例积分微分(PID)控制对叶片挥舞方向位移的控制作用。上述研究均建立了风力机叶片的气弹模型,并对其进行了相应控制,但所建模型不能有效模拟风力机大型化引起的复杂气弹特性,控制性能也有待提高。
笔者以带有尾缘襟翼的美国可再生能源实验室(NREL)5 MW参考风力机为研究对象,综合考虑了大型风力机叶片的旋转、重力、阻尼和气弹耦合等因素,建立了较为全面的智能叶片挥舞气弹模型(以下简称气弹模型),并与FAST气弹仿真平台(以下简称FAST平台)进行了对比仿真,以验证所建模型的准确性。在上述模型的基础上,提出了基于最小均方(LMS)主动控制算法(以下简称LMS算法)的尾缘襟翼主动控制方法,对湍流风况下的叶尖偏移量进行控制。
1 建模对象
研究对象为NREL 5 MW参考风力机,在叶片上添加了独立的尾缘襟翼执行机构,建立了带有尾缘襟翼的气弹模型。
1.1 NREL 5 MW参考风力机
NREL 5 MW参考风力机有3个叶片,属于迎风式变速变桨风力机,其叶片由8种不同的翼型组成。NREL 5 MW参考风力机的主要参数见表1[9]。
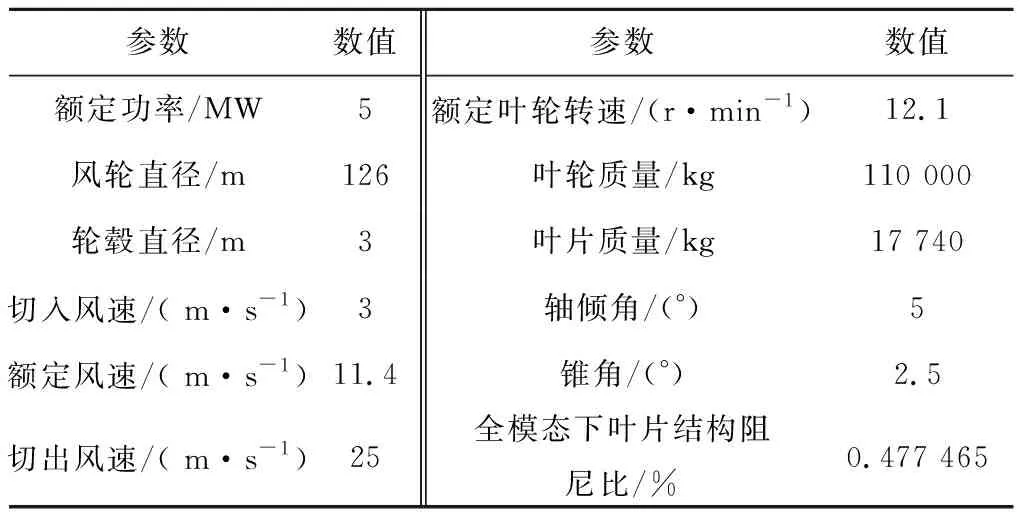
表1 NREL 5 MW参考风力机参数
1.2 尾缘襟翼执行机构
NREL 5 MW参考风力机叶片总长为61.5 m。将叶片分为30个叶素段,并参考文献[10]中的最优尾缘襟翼参数,在叶片第23~29叶素段上增加尾缘襟翼,带有尾缘襟翼的叶片结构如图1所示。尾缘襟翼执行器动作存在延迟,导致其对尾缘襟翼的控制存在滞后。将尾缘襟翼执行机构视为一阶惯性环节。

图1 风力机叶片及尾缘襟翼示意图
1.3 风力机坐标系
为准确描述风力机叶片在旋转时的运动状态,以旋转叶片为参考系,建立了运动坐标系,如图2所示。选取沿叶片展向向外的方向为x轴正方向,y轴为叶片旋转的切线方向,z轴为垂直于叶轮平面的方向,使该坐标轴符合右手定则。
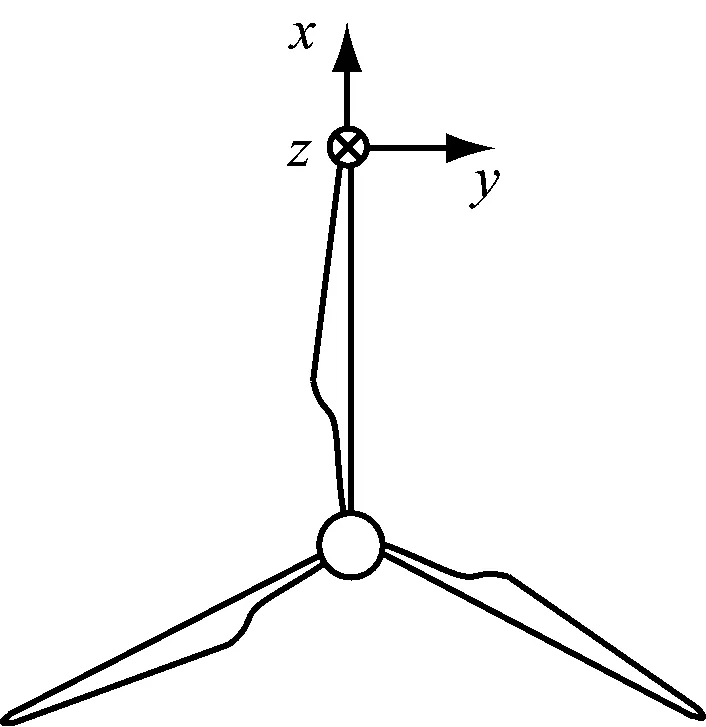
图2 风力机叶片坐标系示意图
2 智能叶片气弹建模
尾缘襟翼主要影响挥舞方向气动载荷,因此主要建立气弹模型,由气动模型、弹性模型和气弹耦合计算方法这3部分组成。
2.1 气动模型
2.1.1 叶素动量理论
叶素动量理论是较为成熟的气动模型分析方法[11],分为叶素理论和动量理论。在叶素理论中将叶片沿展向分为许多叶素,假设每个叶素上的空气动力学特性相互独立。动量理论是将包含风力机的环形控制体离散为多个环形单元控制体,假设控制体内流体不可压缩且相互独立[12]。根据叶素动量理论可以计算在不同风速、转速和桨距角下叶片所受稳态载荷和推力的变化。
根据叶素动量理论,在已知叶素升力系数Cl和阻力系数Cd的条件下,可以通过局部桨距角求得该段叶素的法向力系数Cn和切向力系数Ct:
(1)
式中:φ为该段叶素的入流角,φ=α+β,其中α为叶片攻角,β为局部桨距角。
通过叶素的法向力系数Cn和切向力系数Ct可求得该段叶素的局部挥舞方向载荷pN和摆振方向载荷pT:
(2)
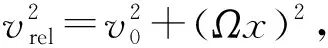
2.1.2 尾缘襟翼对气动模型的影响
带有尾缘襟翼的翼型升力系数Cl和阻力系数Cd随叶片攻角α以及襟翼角γ的变化而改变。设尾缘襟翼偏向z轴正方向时襟翼角为正,反之为负。
在NACA64_A17翼型的基础上,得到不同襟翼角γ下的升力系数Cl和阻力系数Cd。通过Xfoil[13]的分析计算,得到不同襟翼角γ下升力系数Cl和阻力系数Cd随攻角α变化的数据表,从而得到Cl(α,γ)和Cd(α,γ)的二维数据表,可以通过线性插值法查表得到指定攻角α和襟翼角γ下的Cl(α,γ)和Cd(α,γ)。
2.2 弹性模型
叶片弹性建模方法主要有模态法、多体动力学方法和有限元法等,其中模态法由于精度较高、运行速度较快而被广泛应用于风力机叶片气弹模型的研究中。笔者基于模态法,综合考虑了大型风力机叶片的旋转、重力、阻尼和气弹耦合等因素,建立了较为全面的气弹模型。
2.2.1 模态法
在模态参数模型中,以模态频率、模态向量(振型)和衰减系数为特征参数的数学模型可完整描述一个振动系统。模态法是指以振动理论为基础,以模态参数为目标的分析方法[14]。
风力机叶片的振动与其自身的结构属性、边界条件以及外界风速、所受重力和发电机转矩等外来激励有关。为了分析较为复杂的振动,通常将其分解为几个与外来激励无关的简单振动组合,这些简单振动就是振型。振型函数是通过分析计算叶片的结构数据特征而得出的一个近似函数,用于表示振动形状。为了精确描述智能叶片运动,使用N阶广义坐标系描述叶片振动系统。将q(t)定义为系统的广义坐标向量:
(3)
式中:qi(t)为叶片第i个挥舞振动振型对应的广义坐标,其中i=1,2,…,N。
根据广义坐标向量与振型可以得出在t时刻x点处的叶尖挥舞方向偏移量u(x,t):
(4)
式中:φi(x)为第i阶挥舞方向的本征模态振型函数。
根据广义坐标向量与相应模态γi(x)来描述尾缘襟翼的襟翼角γ:
(5)
2.2.2 叶片挥舞方向的动能
叶片因旋转而受力形变的过程中,旋转产生的速度仅影响叶片摆振方向的动能。则t时刻x点处叶片挥舞方向的偏移速度为v(x,t):
(6)
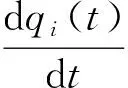
叶片挥舞方向的动能Tb为:
(7)
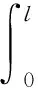
2.2.3 叶片挥舞方向的势能
叶片在受外力的运动过程中,外力所做的功一部分转化为储存在叶片内的势能。叶片储存的总势能由弯曲应变能、离心力势能以及重力势能组成。
(1)叶片受到外力作用产生挥舞方向的形变,因此一部分外力做的功转化为叶片弯曲产生的弯曲应变能。根据叶片挥舞方向的弯曲形状和弯曲刚度,叶片挥舞方向的应变ε为:
(8)
式中:z为该段叶片与形心坐标轴的距离。
叶片挥舞方向的应力为σ=Eε,其中E为叶片的弹性模量。叶片挥舞方向的弯曲应变能Vε为:
(9)
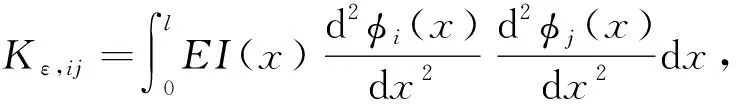
(2)叶片受离心力作用产生轴向形变,离心力使叶片在轴线方向产生离心力势能。离心力Fr(x)为:
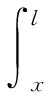
(10)
叶片的轴向形变量s为:
(11)
式中:L为该段叶片形变后的长度。
叶片离心力势能Vr为:
(12)
(3)叶片受重力作用也会产生形变,重力使得叶片在轴线方向产生重力势能。重力的轴向分力G(x)为:

(13)
式中:g为当地重力加速度。
叶片的重力势能Vg为:
(14)
综上,叶片挥舞方向总势能V为:
V=Vε+Vr+Vg
(15)
2.2.4 叶片挥舞方向的耗散能
在振动过程中,叶片受结构阻尼作用产生耗散能,其振动幅度呈衰减趋势。叶片所受的阻尼力FR(x)为:
(16)
式中:ci(x)为阻尼系数,ci(x)=2ζωim(x),其中ζ为叶片结构阻尼比,ωi为叶片第i阶挥舞方向本征模态振型函数对应的固有频率。
耗散能D为:
(17)
2.2.5 叶片挥舞方向广义载荷的虚功
叶片受外界载荷作用所做的总虚功由气动载荷、离心力载荷和重力载荷所做的虚功组成。
(1)叶片挥舞方向受到的气动载荷是叶片发生挥舞振动的主要原因。根据虚位移原理[15]可以得到叶片挥舞方向气动载荷pN所做的虚功Wp:
(18)
(2)叶片受外力作用发生旋转后会受到离心力的作用。当考虑叶片形变时,叶片挥舞方向将受到离心力分力的作用,使其挥舞偏移量减小。叶片每段叶素所受的离心力载荷pr(x)为:
(19)
叶片挥舞方向离心力载荷所做的虚功Wr为:
(20)
(3)与离心力类似,叶片所受重力载荷也对挥舞方向的偏移量产生影响。叶片每段叶素所受的重力载荷pg(x)为:
(21)
叶片挥舞方向重力载荷所做的虚功Wg为:
(22)
综上,叶片挥舞方向广义载荷的总虚功Wb为:
Wb=Wp+Wr+Wg
(23)
2.2.6 尾缘襟翼对弹性模型的影响
尾缘襟翼主要影响智能叶片弹性模型叶片相应位置的质量和刚度分布,会改变叶片的总动能和叶片所受的总虚功等。通常尾缘襟翼对叶片质量分布以及叶片基线刚度的影响较小,一般可以忽略[16]。笔者主要研究尾缘襟翼运动过程中产生的动能及其克服空气动力做功对智能叶片弹性模型的影响。
尾缘襟翼在受主动控制力作用进而改变襟翼角时,襟翼绕主轴旋转产生动能,其挥舞方向的动能TH为:
(24)
式中:lγ为尾缘襟翼的展向长度;ρH为尾缘襟翼材料密度;cH为尾缘襟翼弦长,尾缘襟翼占弦比为25%,因此cH=c/4。
智能叶片挥舞方向的总动能T为:
T=Tb+TH
(25)
尾缘襟翼受空气动力作用而产生绕尾缘襟翼主轴的力矩MH:
(26)
式中:CH(γ)为气动力铰链力矩系数。
为克服空气动力作用并改变襟翼角,尾缘襟翼所做的虚功为:
(27)
智能叶片在挥舞方向的总虚功W为:
W=Wb+WH
(28)
2.3 气弹耦合计算方法
由于大型风力机的叶片柔性增强,气动力、惯性力和弹性力等的耦合作用不可忽略,叶片所受气动载荷会使叶片产生形变,叶片的形变会进一步改变叶片周围流场,进而使气动载荷产生变化。带有尾缘襟翼的智能叶片随着来流风速和叶片气弹情况发生变化,尾缘襟翼受主动控制力作用,使得襟翼角发生改变,从而影响智能叶片的气弹特性。因此,在带有尾缘襟翼的智能叶片气弹耦合过程中,襟翼角变化会引起翼型变化,进而会与叶片气动模型以及弹性模型三者相互作用,最终达到动态平衡。智能叶片的气弹耦合计算方法的流程如图3所示。
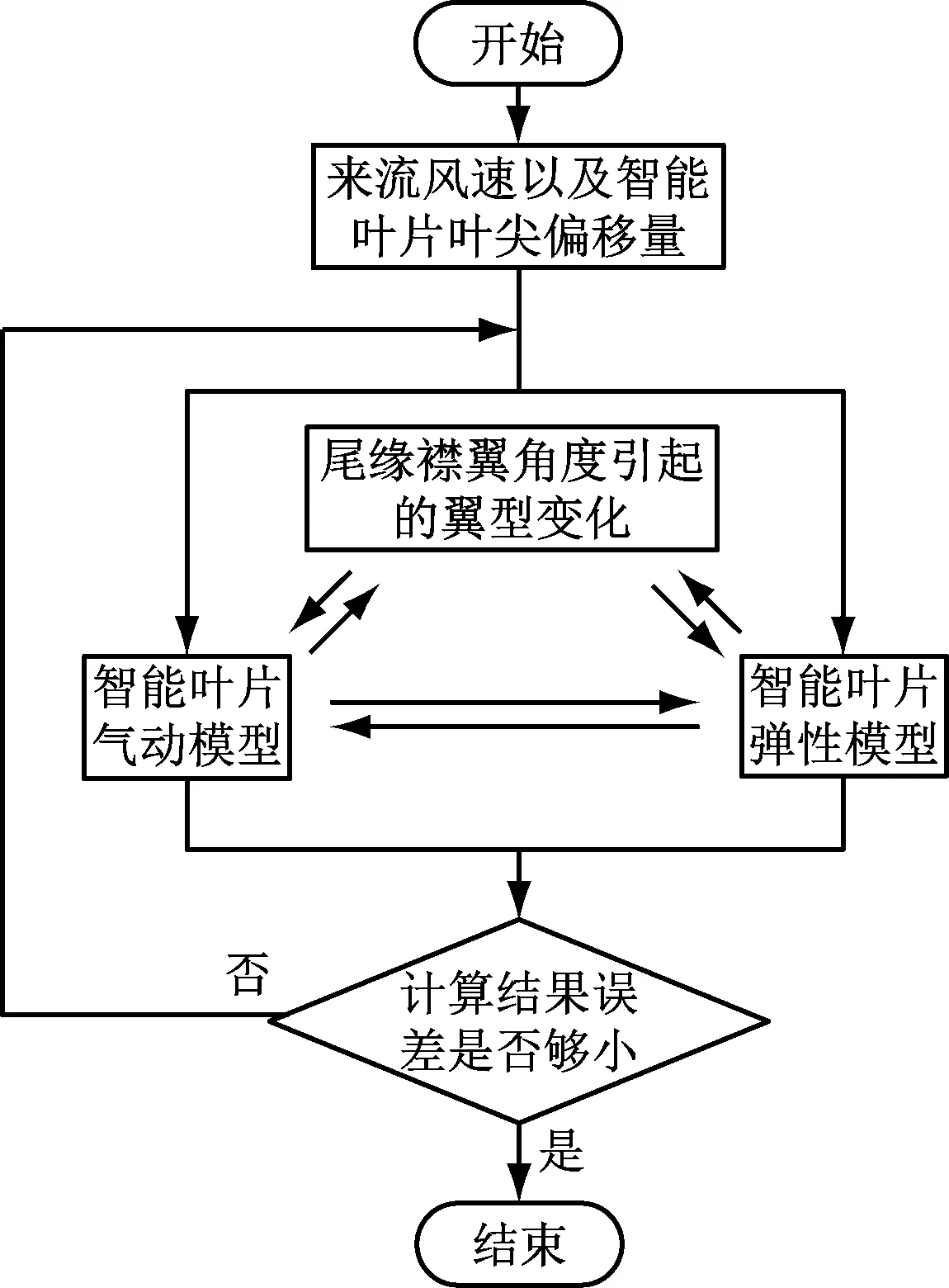
图3 智能叶片气弹耦合计算方法流程图
2.4 智能叶片挥舞方向气弹建模
根据拉格朗日方程,智能叶片挥舞方向的系统运动方程可由动能T、势能V、耗散能D以及所受广义力Q表示:
(29)
Q=Qp+Qr+Qg+QH
式中:q为叶片广义坐标;Qp为叶片挥舞方向气动广义载荷;Qr为叶片挥舞方向离心力广义载荷;Qg为叶片挥舞方向重力广义载荷;QH为叶片尾缘襟翼控制力广义载荷。
气弹模型为:
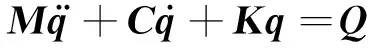
(30)
其中,
K1,i=Kε,i-Ω2mi+
笔者使用模态法建立了气弹模型。模态法使用的模态阶次越高,气弹模型越精确,但所需时间也越长。叶片达到更高阶模态所需的能量较多,难以被激励,因此气弹模型选用前3阶模态。
3 气弹模型验证
FAST平台[17]是由NREL开发的风力机气弹仿真平台,其经过GL认证,计算结果准确度较高。笔者在风力机使用标准变速变桨控制的条件下,将建立的气弹模型与带有尾缘襟翼的FAST平台[10]进行了对比仿真验证。
3.1 多种风况下气弹模型准确性验证
仿真时间为480 s,风况为每隔60 s阶跃增加的区域2稳定风况(轮毂高度风速变化范围为4~11 m/s)。图4和图5分别给出了气弹模型与FAST平台叶尖偏移量和叶根挥舞弯矩的变化情况。与FAST平台相比,气弹模型的叶尖偏移量偏差约为5.42%,叶根挥舞弯矩偏差约为5.33%。
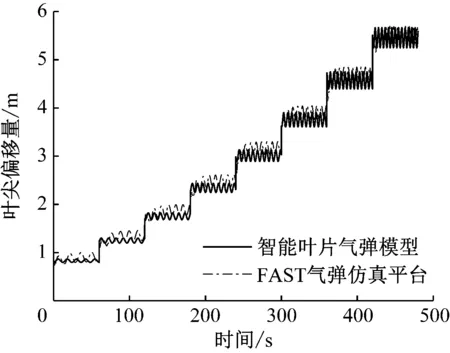
图4 区域2稳定风况下的叶尖偏移量
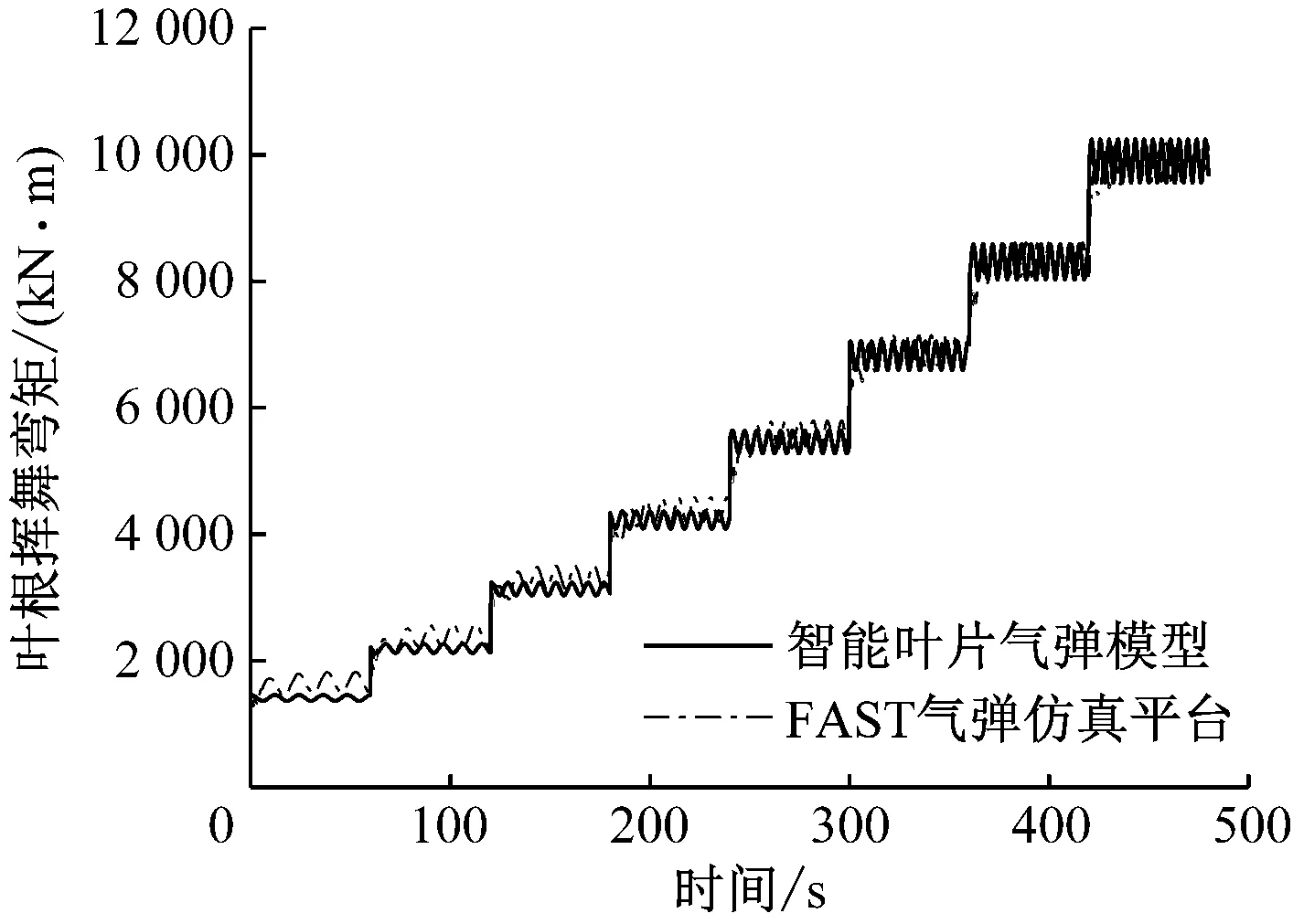
图5 区域2稳定风况下的叶根挥舞弯矩
仿真时间为1 400 s,风况为每隔100 s阶跃增加的区域3稳定风况(轮毂高度风速变化范围为12~24 m/s)。图6和图7分别给出了气弹模型与FAST平台叶尖偏移量和叶根挥舞弯矩的变化情况。与FAST平台相比,气弹模型的叶尖偏移量偏差约为2%,叶根挥舞弯矩偏差约为6.4%。
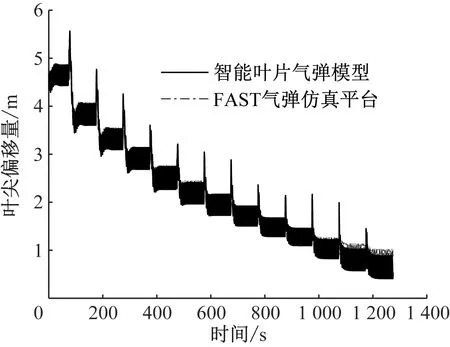
图6 区域3稳定风况下的叶尖偏移量
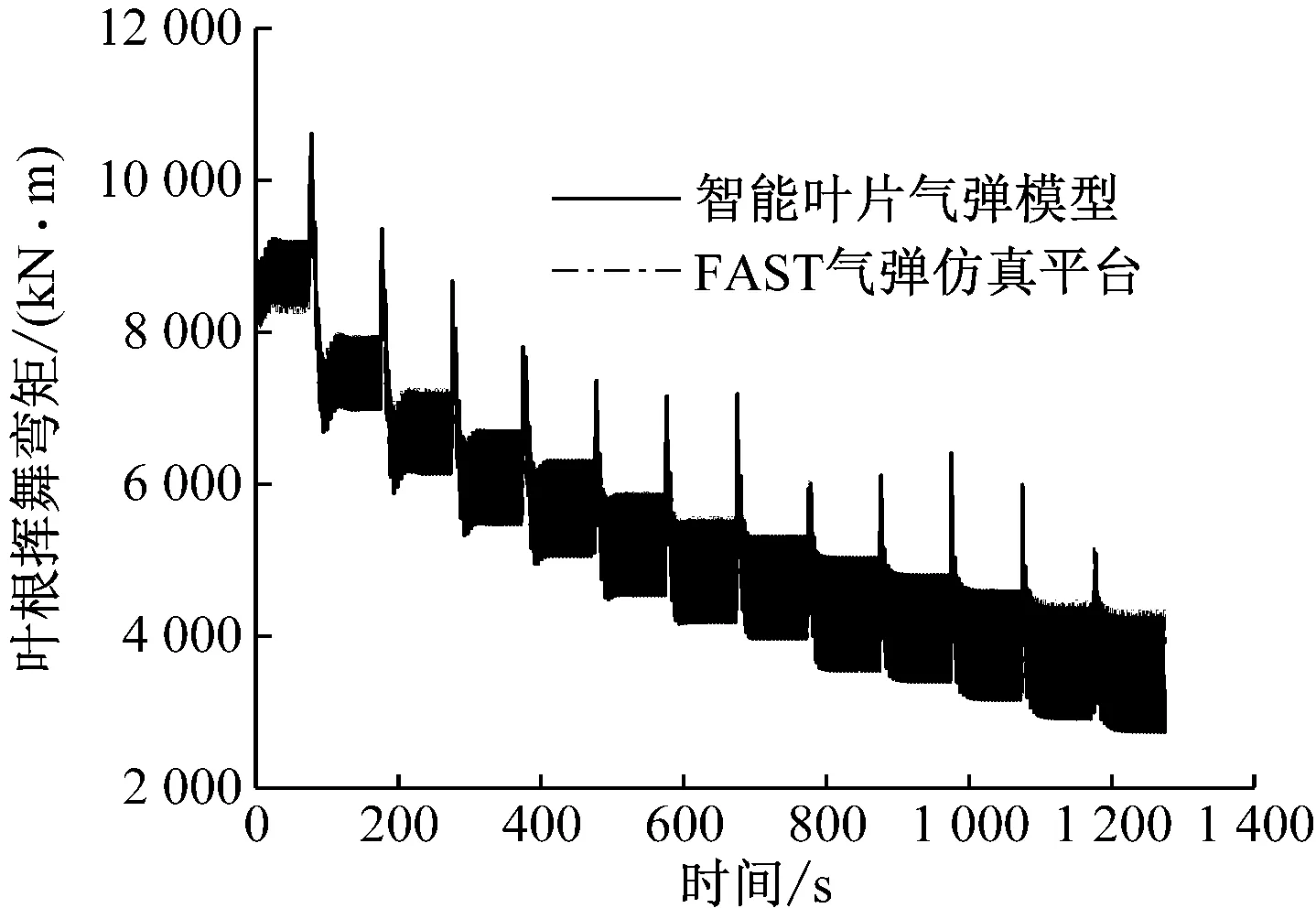
图7 区域3稳定风况下的叶根挥舞弯矩
仿真时间为325 s,风况为轮毂高度平均风速为11.4 m/s、湍流强度为5%的标准湍流风况。图8和图9分别给出了气弹模型与FAST平台叶尖偏移量和叶根挥舞弯矩的变化情况。与FAST平台相比,气弹模型的叶尖偏移量偏差约为4.31%,叶根挥舞弯矩偏差约为4.29%。
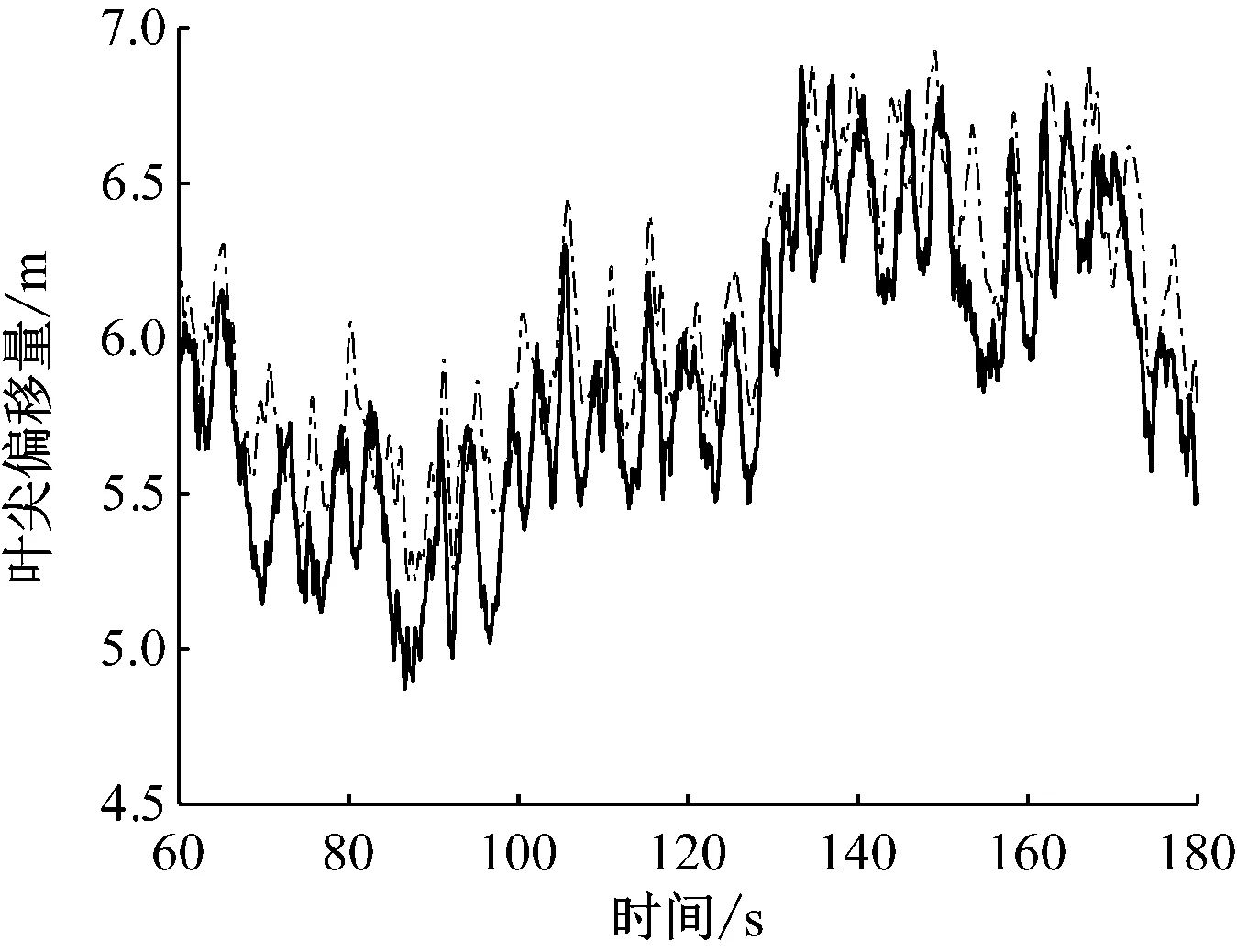
图8 标准湍流风况下的叶尖偏移量
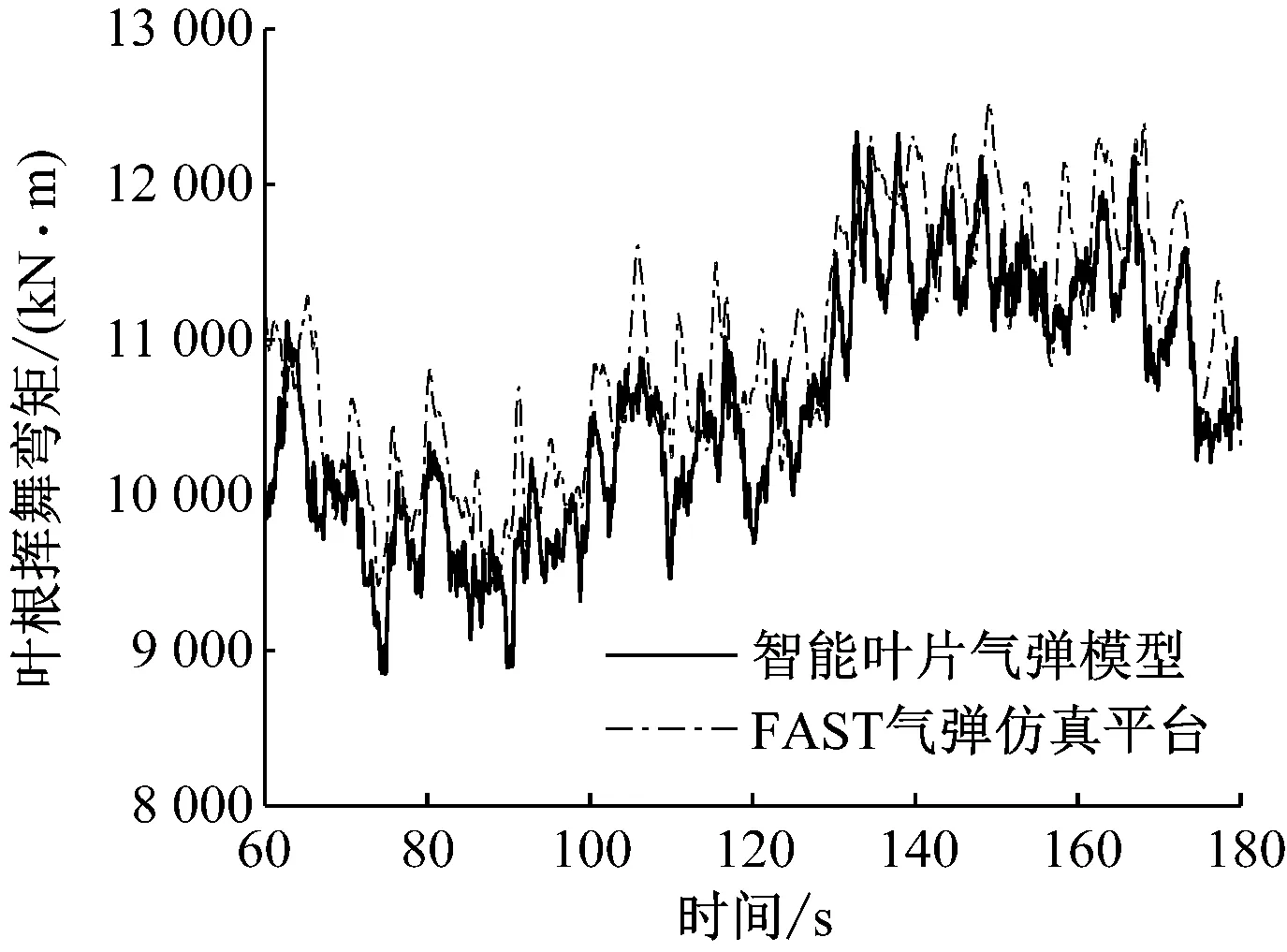
图9 标准湍流风况下的叶根挥舞弯矩
综上,在整个风力机工作范围的稳定风况以及标准湍流风况下,所建立的气弹模型都有较高的精度。
3.2 11.4 m/s稳定风况不同襟翼角下叶尖偏移量及叶根挥舞弯矩的对比
在轮毂高度处风速为11.4 m/s的稳定风况下,叶尖偏移量和叶根挥舞弯矩随襟翼角的变化如图10所示。当襟翼角为负时,挥舞方向叶尖偏移量和叶根挥舞弯矩均明显减小;当襟翼角为正时,挥舞方向叶尖偏移量和叶根挥舞弯矩均明显增大。襟翼角对叶尖偏移量和叶根挥舞弯矩的影响较大,说明通过控制襟翼角,可对叶片的叶尖偏移量和叶根挥舞弯矩进行调节。
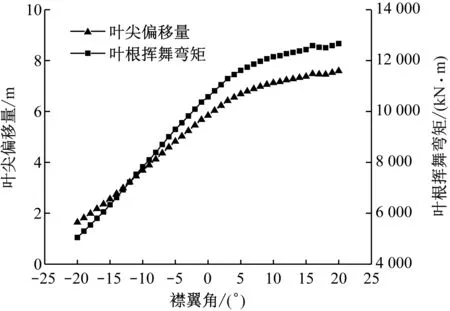
图10 11.4 m/s稳定风况下叶尖偏移量和叶根挥舞弯矩随襟翼角的变化
Fig.10 Blade tip deflection & flapwise root moment vs. trailing edge flap angle at stable wind of 11.4 m/s
4 尾缘襟翼主动控制仿真
自适应滤波算法能快速有效地自动辨识系统模型,其中LMS算法可以自适应调节权系数,计算简单,可应对多种复杂工况,在抵消噪声和振动控制等领域得到广泛应用[18]。笔者基于LMS算法设计了尾缘襟翼主动控制器,在湍流风况下对叶尖偏移量进行了控制。
4.1 基于LMS算法的尾缘襟翼主动控制系统
将k时刻的参考叶尖偏移量d(k)与叶尖偏移量y(k)的差值e(k)作为LMS控制器的输入,通过LMS控制器得到控制所需的襟翼角γ(k),通过所建的气弹模型得到k+1时刻的叶尖偏移量y(k+1),如此反复进行,其中气弹模型所处的风速v(k)视为系统扰动。图11给出了基于LMS算法的尾缘襟翼主动控制系统框图。
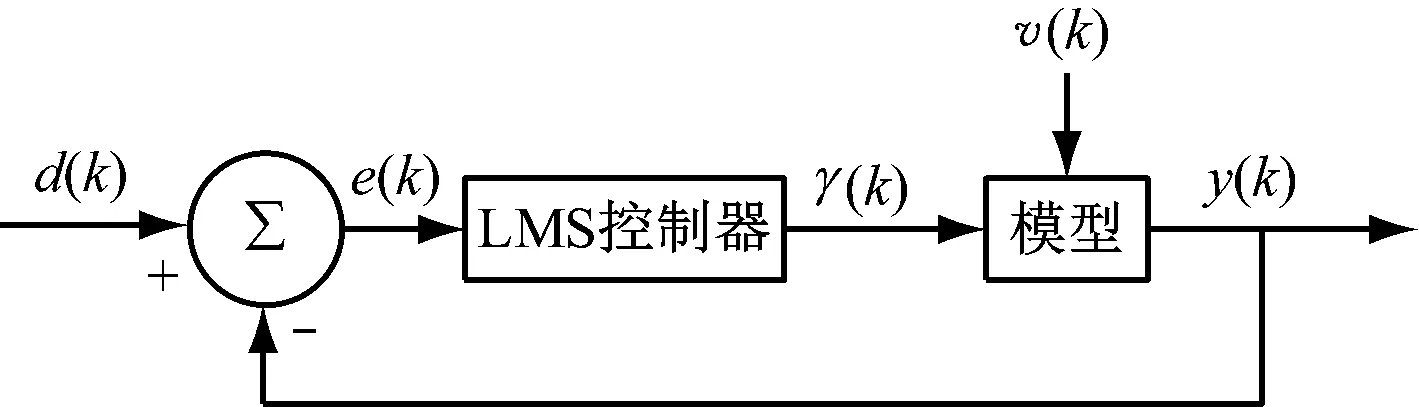
图11 智能叶片LMS控制系统框图
4.2 叶尖偏移量控制
采用图1所示的尾缘襟翼结构,在湍流风况下利用基于LMS算法的尾缘襟翼主动控制方法对叶尖偏移量进行控制,以削弱由风况变化等原因导致的叶片形变和减小叶片疲劳载荷。
仿真时间为250 s,风况为轮毂高度平均风速为11.4 m/s、湍流强度为3%的标准湍流风况。
在标准湍流风况下,对在LMS控制、PID控制和无控制下尾缘襟翼的叶尖偏移量进行对比,如图12所示,其中LMS控制和PID控制均从50 s开始。由图12可知,LMS控制和PID控制均对叶片叶尖偏移量有较好的控制效果,可减小叶尖偏移量的振动幅度波动和叶片的疲劳载荷。
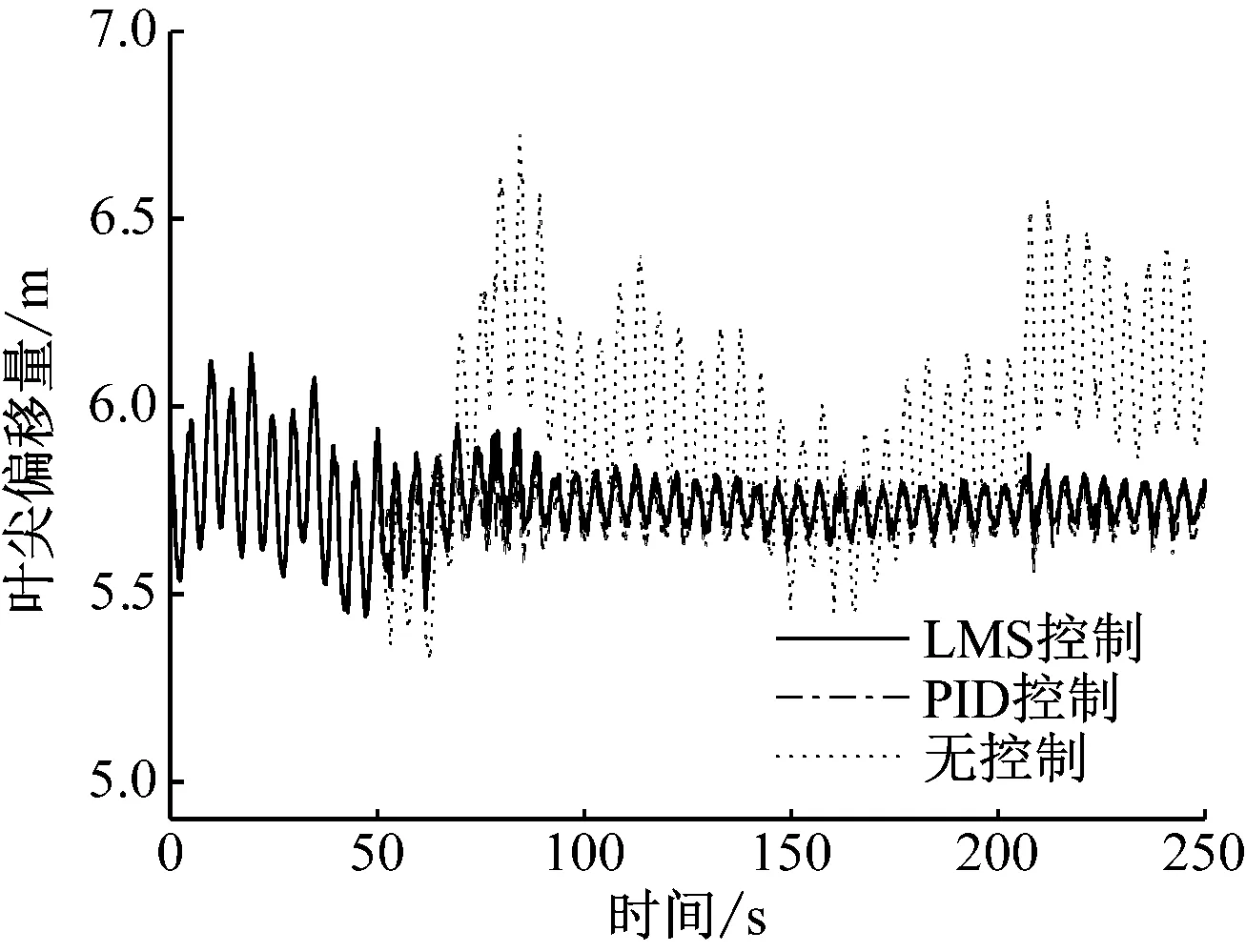
图12 LMS控制、PID控制和无控制下的叶尖偏移量变化
Fig.12 Comparison of blade tip deflection with LMS control, PID control or without control
在LMS控制、PID控制和无控制下襟翼角的变化如图13所示。LMS控制在控制开始阶段有自适应辨识过程,这段时间内控制量逐渐增大,控制效果逐渐增强。控制器达到稳定状态后,LMS控制和PID控制下的襟翼角变化趋势大致相同,对叶尖偏移量起到了有效控制作用。表2给出了LMS控制、PID控制与无控制下叶尖偏移量的标准偏差。由表2可知,LMS控制和PID控制能有效减小叶片叶尖偏移量的波动,LMS控制下叶尖偏移量的波动更小,较PID控制下叶尖偏移量的标准偏差减小25.60%。
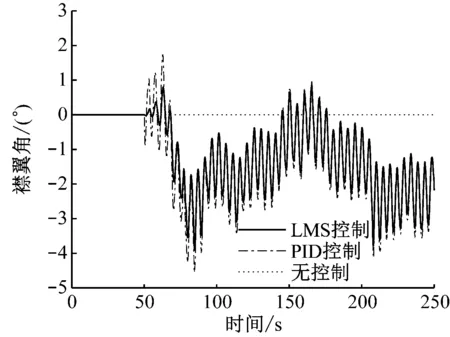
图13 LMS控制、PID控制和无控制下襟翼角的对比
图14给出了LMS控制与无控制下叶根挥舞弯矩的变化, LMS控制不仅控制叶尖偏移量,还可以有效控制叶根挥舞弯矩。
表2LMS控制、PID控制和无控制下叶尖偏移量的标准偏差
Tab.2StandarddeviationofbladetipdeflectionwithLMScontrol,PIDcontrolorwithoutcontrol

控制情况LMS控制PID控制无控制标准偏差0.041 80.052 50.247 0

图14 LMS控制和无控制下叶根挥舞弯矩的变化
5 结 论
(1)与FAST平台相比,在风力机正常工作的稳定风况以及标准湍流风况下气弹模型的叶尖偏移量和叶根挥舞弯矩的误差均不超过7%,气弹模型精度较高。
(2)在11.4 m/s的稳定风况下,随着襟翼角的变化,叶尖偏移量和叶根挥舞弯矩也产生较大变化,这说明控制襟翼角可有效调节叶尖偏移量和叶根挥舞弯矩。
(3)在平均风速为11.4 m/s的标准湍流风况下,基于LMS算法的尾缘襟翼主动控制方法可有效减小叶尖偏移量波动和疲劳载荷,与PID控制相比,其叶尖偏移量的标准偏差减小25.60%,说明基于LMS算法的尾缘襟翼主动控制方法能更有效地减小叶尖偏移量的波动。
