基于二次相关PHAT-β算法的锅炉声学测温时延估计研究
2018-08-29沈国清杨杰栋刘伟龙张世平安连锁
沈国清, 杨杰栋, 陈 栋, 刘伟龙, 张世平, 安连锁
(1. 华北电力大学 电站设备状态监测与控制教育部重点实验室, 北京 102206; 2. 华北电力大学 国家火力发电工程技术研究中心, 北京 102206)
声学测量作为一种非接触式测量手段,在工程应用领域前景广阔。在燃煤电站中,由于炉膛内部环境恶劣,测量场不透明,利用声学技术的监测手段得到了广泛关注,基于声学技术的产品也相继问世。
沈国清等[1-2]研究了声学测温技术,实现了炉膛温度的实时测量,通过重建算法可视化炉内温度场,对稳燃和降低NOx排放具有指导意义。李言钦等[3-4]研究了声波在炉内速度场的传播,重建了炉内二维速度场。安连锁等[5-6]研究了时延估计在炉内声学监测中的应用,讨论了声源位置、声源声压级、炉膛噪声等因素对估值的影响。姜根山等[7-8]研究了炉膛四管泄露的声传播特性,以及利用传声器阵列对泄露点的监测与定位算法。
上述声学监测手段的基础是获得声源在2个或多个传声器阵列间的传播时间,即时延估计。时延估计的精度直接影响测量结果的精度。时延估计在信号处理领域具有极其重要的地位,可应用于声呐探测、地质勘探、语音识别、气象测量、工业控制和通信传输等领域[9]。自1980年起,美国电气和电子工程师协会( IEEE)发表了时延估计专栏,时延估计理论得到深入的发展,根据不同的应用环境,建立了广义互相关时延估计、二次相关时延估计、自适应时延估计、希尔伯特时延估计和高阶统计量时延估计等方法[10-12]。
虽然时延估计在信号处理领域中得到了充分发展,但在电站锅炉声学测量中的研究相对较少。目前,声学测温技术已在国内多家电厂得到应用,实际运行的情况显示,在冷态传声器位置标定时,混响对时延估计的影响较大,实验人员需要多次测量才能确定传声器间的相对位置,针对这一问题,笔者提出了一种基于二次相关的时延估计新算法即二次相关相位变换加权(PHAT-β)算法,在实验室搭建的炉膛和国内某300 MW机组上进行实验,以验证该算法的可行性,这对声学测温及声学测量在电站锅炉中的应用优化具有重要意义。同时,该算法的时延估计还可以用于泄露定位、声呐探测、地质勘探和气象测量等领域。
1 声学测温时延估计模型
电站锅炉声学测温技术通过在炉膛截面布置多路传声器与声源进行测量,如图1所示(其中1~8表示布置在炉膛截面的8个测点位置),两两测点间形成多条声传播路径,利用时延估计算法得到每一条路径的声波传播时间,再根据传播时间反演出炉内温度场,具体的重建算法详见文献[1]和文献[2]。笔者主要研究时延估计算法,因此以某单一路径为例,简化的时延估计模型如图2所示。

图1 声学测温路径

图2 时延估计模型
对于离散时延估计系统,单一路径简化的数学模型为:
x1(n)=s(n)+n1(n)
(1)
x2(n)=αs(n-D)+n2(n)
(2)
式中:x(n)为传声器接收到的信号;s(n)为信号;n(n)为加性噪声信号;α为声传播的衰减系数;D为时延估计;下标1、2分别表示通道1和通道2。
2 时延估计算法
2.1 直接相关时延估计
利用直接相关法求取信号模型x1(n)与x2(n)的相关函数:
Rx1,x2(τ)=E[x1(n)x2(n+τ)]
(3)
式中:E为期望;τ为理论上的时间延迟。
式(3)简化后的结果为:
Rx1,x2(τ)=Rs,s(τ-D)+Rs,n1(τ-D)+
Rs,n2(τ)+Rn1,n2(τ)
(4)
式中:Rs,s(τ-D)为信号与信号的相关函数;Rs,n1(τ-D)、Rs,n2(τ)分别为信号与通道1和通道2的相关函数;Rn1,n2(τ)为噪声与噪声的相关函数。
若加性噪声是理想的高斯白噪声,那么信号与噪声、噪声与噪声间不相关,则
Rs,n1(τ-D)=Rs,n2(τ)=Rn1,n2(τ)=0
(5)
式(4)最终简化为:
Rx1,x2(τ)=Rs,s(τ-D)
(6)
当τ=D时,相关函数取得最大值,利用采集卡得到的峰值d为时延估计的点数,d除以采样频率便可得到时延估计D,如图3所示。

图3 时延估计
但在实际测量中,n1(n)与n2(n)通常不是理想的高斯白噪声,同时考虑混响的影响,Rs,n1(τ-D)、Rs,n2(τ)和Rn1,n2(τ)通常不为0,因此直接相关法的时延估计不准确。
2.2 二次相关时延估计
唐娟等[13]提出了二次相关的时延估计算法。其实质是将x1(n)的自相关函数Rx1,x1(τ)与x1(n)、x2(n)的互相关函数Rx1,x2(τ)再进行二次相关,由于相关函数也是时间的函数,因此可将τ换作n,将Rx1,x1(n)、Rx1,x2(n)作为新的信号序列,得到二次相关函数:
RR,R(τ)=E[Rx1,x1(n)Rx1,x2(n+τ)]
(7)
类似于式(3)的简化过程,具体推导过程详见文献[13],式(7)可简化为:
RR,R(τ)=RR,S(τ-D)+RR,N(τ)
(8)
式中:RR,S(τ-D)为纯信号s(n)的二次相关函数,RR,N(τ)为噪声的二次相关函数。
在理想情况下,噪声为非相关的高斯白噪声,因此RR,N(τ)=0,与直接相关法类似,在τ=D时,RR,R(τ)取得最大值,便能得到时延估计。相较于直接相关法,二次相关算法在计算过程中减少了噪声的影响,同时适用于更低的信噪比。但在噪声相关的情况下,RR,N(τ) 不能忽略,因此运用直接相关法和二次相关算法在低信噪比下的时延估计准确性大大降低,但总体来说,二次相关算法在一定范围内优于直接相关法。
2.3 广义互相关
由于噪声和混响等因素的影响,直接相关法不能得到准确的时延估计,因此Knapp等[10]利用广义互相关(GCC)对直接相关法进行改进。广义互相关的实质是将采集到的离散时域信号转换到频域进行分析,求取信号的互功率谱函数,并对其进行加权,加权的作用等效于对信号进行预滤波,从而抑制噪声的影响,同时提高信噪比中的高频成分。由Wiener-Khinchin定理可知,互功率谱函数与相关函数为傅里叶变换对,因此对加权后的互功率谱函数进行反傅里叶变换便能求得相关函数,再进行峰值检测便可得到时延估计。
其中,互功率谱函数为:
Gx1,x2=F*[x1(n)]F[x2(n)]
(9)
式中:F表示傅里叶变换(FFT);*表示共轭。
广义互相关函数可表示为:
Rx1,x2(τ)=F-1[ψ(f)Gx1,x2(f)]=

(10)
式中:F-1表示傅里叶逆变换;ψ(f)为权函数,常见的广义互相关权函数见表1,其中|γ12(f)|为两传声器接收信号的模平方相干函数。

表1 权函数
笔者以GCC-PHAT算法为参考,最终的相关函数为:
(11)
再对相关函数进行峰值检测便能得到GCC-PHAT算法的时延估计。
3 二次相关PHAT-β算法
GCC-PHAT算法和二次相关算法都能不同程度地降低噪声对时延估计的影响,但二者都存在各自的局限性。GCC通过权重(等效于对信号与噪声进行白化处理)提高信噪比,但当信噪比较低时,时延估计精度大大降低。二次相关算法通过相关函数抑制噪声影响,具有较好的抗噪性能,但其时延估计精度有待提高。
在二次相关与GCC的基础上,笔者提出了基于二次相关的PHAT-β广义互相关算法,即二次相关PHAT-β算法,其流程图如图4所示。

图4 二次相关PHAT-β算法流程图

GRx=F*[Rx1,x1(n)]F[Rx1,x2(n)]
(12)
将加权后的互功率谱函数反变化到时域,进行峰值检测便能得到时延估计。
4 实验研究
由于仿真所选取参数均为抽象的数学模型,而混响、噪声等外界影响均难以用数学模型来表示,因而无法切实地反映实际工程中的问题,前序的理论研究已经证明了二次相关PHAT-β算法的实用性,故直接通过实验来验证该算法的可行性。为了检测二次相关PHAT-β算法的优势,笔者在实验锅炉和某300 MW机组上进行了测温验证,并将二次相关PHAT-β算法与二次相关算法、GCC-PHAT算法进行了对比。
4.1 实验介绍
笔者搭建的声学测温实验台结构如图5所示,锅炉模型长、宽和高分别为5 m、4 m和3 m,在初始条件下,标定测点间的距离以及当地静止声速。采集卡为NI-4431,其同步采样率为102.4 kHz,实验选取采集卡的最大采样率为102.4 kHz,采样点数为65 536。声信号必须选取与炉膛噪声非相关的信号,由文献[14]可知,在电站锅炉前序实验中,将扫频信号作为声源信号的优越性已经得到了充分论证,因此笔者直接选取线性扫频信号作为声源信号[14],扫频信号表达式为:
(13)
式中:f(0)为0时刻瞬时频率;f(τ′)为τ′时刻瞬时频率;[0,τ′]为扫频信号周期。

(a) 外部示意图(b) 内部示意图
图5 测温实验台
Fig.5 Experiment apparatus for temperature measurement
本实验扫频信号的频率选为500~8 000 Hz,扫频周期为100 ms。通过sabine混响时间经验公式计算可得,测温实验台混响时间大于1 s,为强混响声场。
4.2 实验锅炉冷态实验
首先在自由空间下验证几种算法的时延估计,自由空间为开放的环境,声播为自由声场,传声器间的距离为2 m,声源与传声器在同一直线上,其时延估计结果如图6所示。
由图6可知,在自由声场下,3种算法的时延估计均相同,均能获得准确的时延估计。二次相关算法的相关函数旁瓣峰值相对较高,但不影响时延估计的结果,GCC-PHAT算法与二次相关PHAT-β算法的时延估计峰值尖锐。
求取自由空间下的时延估计是为了测定当地声速值,根据3种算法的时延估计结果测得当地声速值为343.16 m/s。
求取自由空间下的时延估计后,在测温实验台进行实验,其时延估计结果如图7所示。实验中选取图1中的测点3和测点7为例,2个测点间的距

(a) 二次相关算法

(b) GCC-PHAT算法

(c) 二次相关PHAT-β算法
离为6 m,由时延估计与当地声速值相乘的结果可知,图7(b)和图7(c)均给出了正确的时延估计峰值。
由图7可知,在强混响环境下,二次相关算法无法得到准确的时延估计,所得时延估计误差较大;GCC-PHAT算法虽然能得到较准确的时延估计,但其旁瓣具有较大的峰值,存在多处伪峰值,在多次采样过程中,由于伪峰值存在,会出现错误的时延估计;而二次相关PHAT-β算法的时延估计峰值尖锐,时延估计准确,且误差较小。由此可见,二次相关PHAT-β算法的时延估计在强混响声场下具有尖锐的时延估计峰值且准确性高。
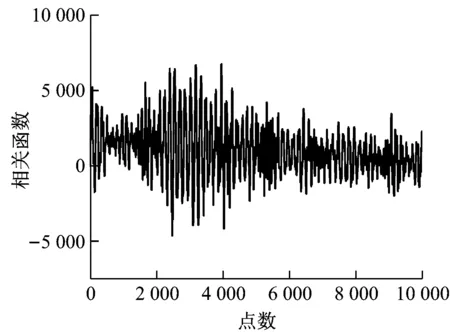
(a) 二次相关算法
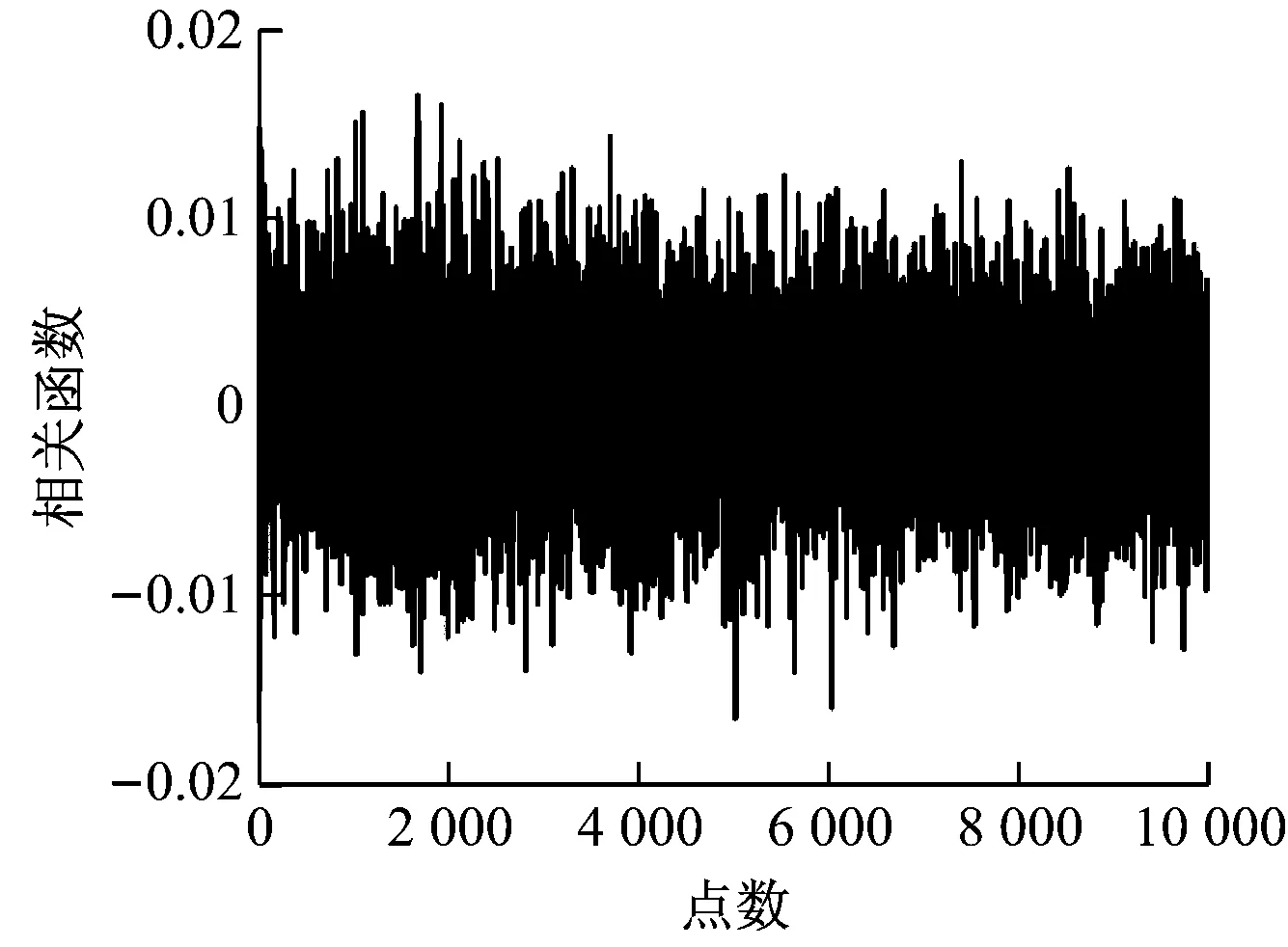
(b) GCC-PHAT算法

(c) 二次相关PHAT-β算法
4.3 300 MW机组冷态时延估计实验
实验炉膛的测试结果显示,二次相关PHAT-β算法能较准确地得到时延估计,同时时延估计峰值较尖锐,在低信噪比的情况下,仍能取得较准确的时延估计。在某300 MW机组锅炉34 m平台截面处布置了多通道传声器(见图1),以其中测点4和测点6为例,进行了时延估计的论证。
在机组停机期间,进行了冷态时延估计的测量,原始波形如图8所示,时延估计结果如图9所示。实验测得该机组当地声速值为340.01 m/s,由于测点4与测点6的空间距离无法直接获得,故采用时延估计求取,2个测点的几何测距计算值为14.6 m。其测量值及相对误差见表2。
由图9和表2可知,二次相关算法的相对误差较大,得到的是错误的时延估计。GCC-PHAT算法的时延估计在正确时延估计附近存在大量伪峰值,且伪峰值高于正确时延估计,因此使得时延估计出现错误,如图9(b)所示。二次相关PHAT-β算法得到了正确、准确的时延估计,且时延估计峰值尖锐,进一步验证了该算法在强混响环境下300 MW机组上的实用性与准确性。

(a) 通道1(b) 通道2
图8 原始波形
Fig.8 Original waveform
4.4 300 MW机组热态时延估计实验
冷态调试完成后,在机组运行时,进行了热态时延估计实验,其结果见图10。由图10及文献[14]

(a) 二次相关算法

(b) GCC-PHAT算法
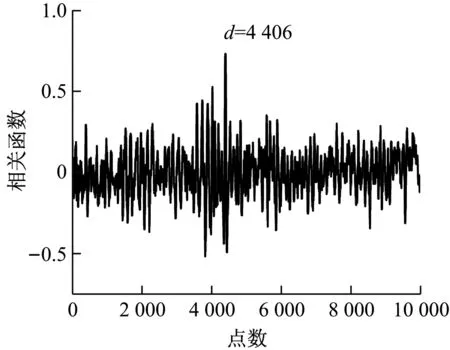
(c) 二次相关PHAT-β算法

算法时延估计/s测量值/m相对误差/%二次相关0.038 066 40612.94311.35GCC-PHAT0.039 414 06213.4028.21二次相关PHAT-β0.043 027 34314.6300.21
可知,炉膛在热态条件下接近于自由声场,混响的影响较小,主要是热态炉膛的强噪声环境对时延估计的影响。由图10还可知,二次相关算法不能得到正确的时延估计峰值,而GCC-PHAT算法及二次相关PHAT-β算法均能在热态环境下得到较准确的时延估计,具有较好的抗噪性能。因此,二次相关PHAT-β算法在强噪声环境下也具有较好的适用性。

(a)二次相关算法
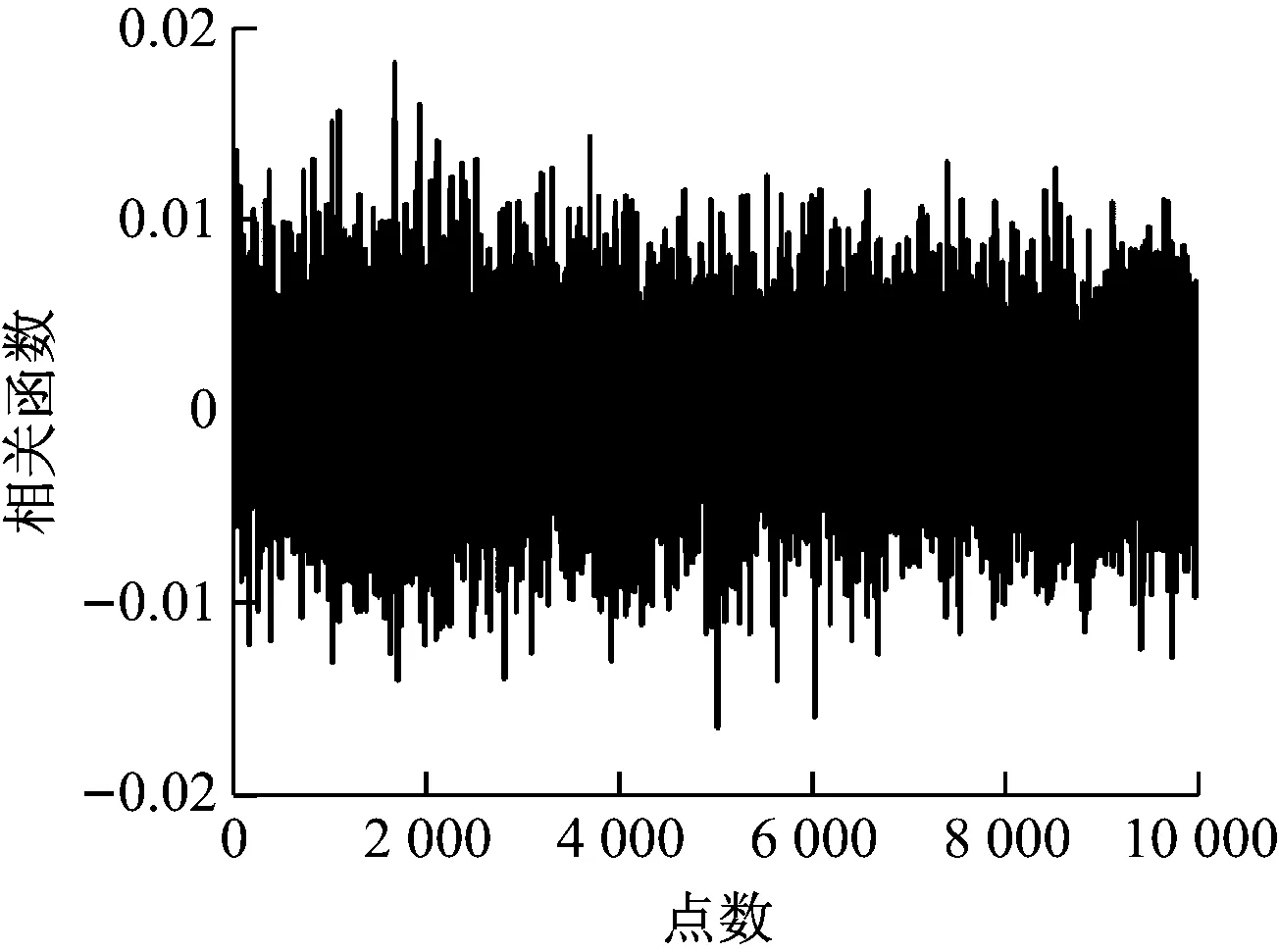
(b)GCC-PHAT算法
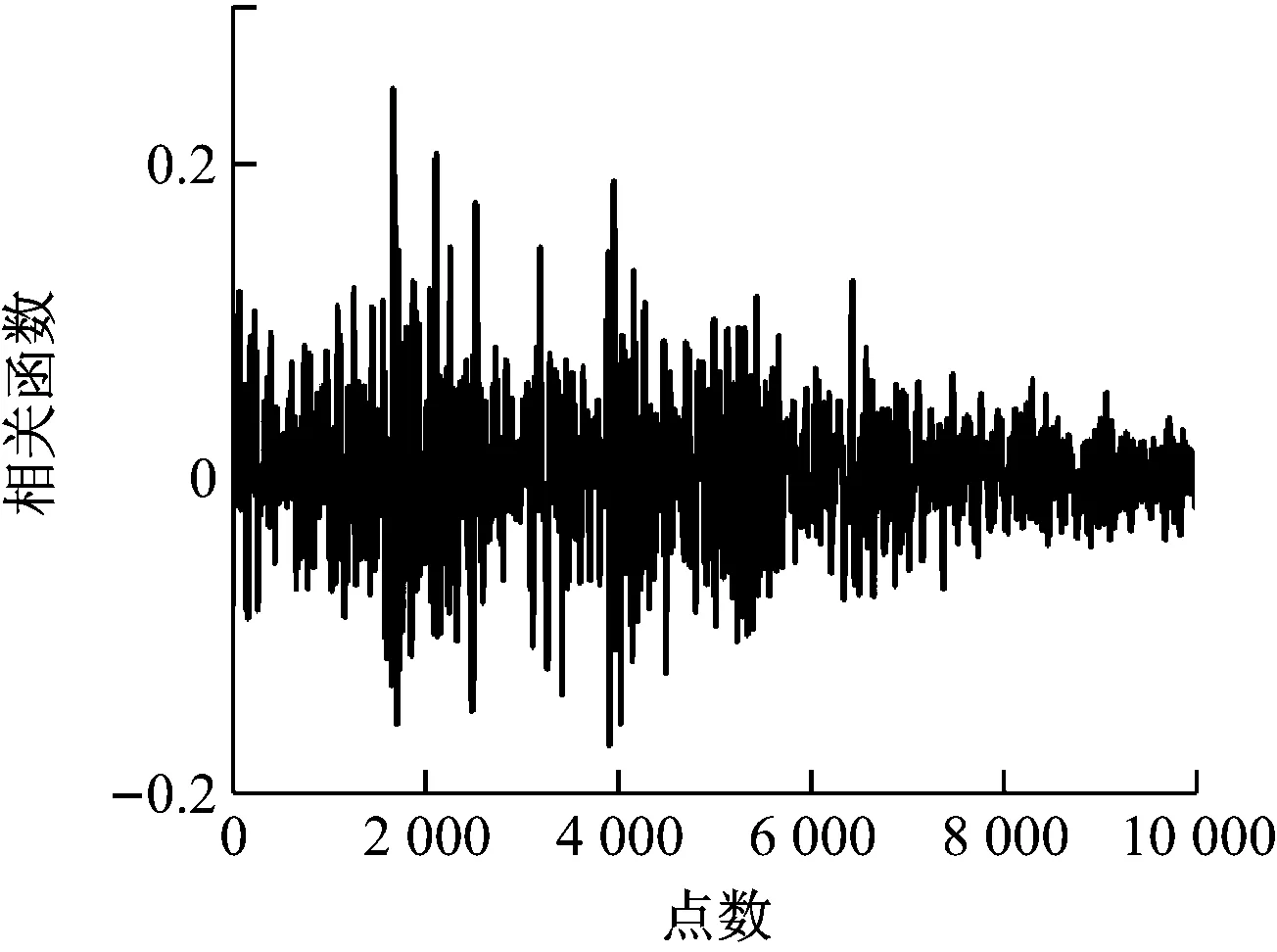
(c) 二次相关PHAT-β算法
上述研究表明,锅炉冷态、热态的实验结果均证明二次相关PHAT-β算法在混响和强噪声环境下均具有较好的适应性能。
5 结 论
提出了一种基于二次相关的PHAT-β算法,在自由声场下,传统时延估计方法与该算法均能得到准确的时延估计。在实验炉膛的强混响环境下,GCC-PHAT算法虽能得到正确时延估计,但存在多处伪峰值,对时延估计的精度有较大的影响,而二次相关PHAT-β算法的时延估计峰值尖锐,具有较强的抗混响能力。在某300 MW机组的冷态、热态实验下,二次相关PHAT-β算法均具有尖锐的时延估计峰值,进一步证明该算法具有较强的抗混响与抗噪能力,为声学测温技术在电站锅炉中的应用提供了一种更为优化的时延估计方案。
