基于非线性补偿的大功率晶闸管整流控制器的研究
2018-08-29彭晓玮李云钢
刘 凯,彭晓玮,李云钢
(1.天津大沽化工股份有限公司,天津 300455;2.湖南科瑞变流股份有限公司,湖南 株洲 412000)
大功率整流器是指功率在10 MW级以上的整流器,主要应用于冶金、化工、石油、造纸、矿山、直流输配电等领域,其常用的半导体器件为二极管和晶闸管[1-3]。晶闸管整流器可以快速调节电压和电流,效率通常在99.5%以上,随着晶闸管整流技术的日趋成熟,晶闸管整流器已成为国内氯碱电解直流电源转换装置的首选[4-6]。随着对控制性能要求的不断提高,需要对控制算法进行深入研究。晶闸管控制系统是一个非线性系统,主要体现在触发角与直流输出平均电压之间是非线性关系[7-8]。此外,由于晶闸管是半控器件,只有当受到反向电压作用才会截止,控制触发信号改变之后并不会立刻起作用,这一短时失控可等价于一个延时环节,它也是一个非线性环节[9]。这些非线性环节会影响全局性能及动态响应特性。对此,文献[10]中提出使用局部线性化,解决了控制角与输出电压的非线性问题,并将延时环节等效为一阶惯性环节,利用线性系统的设计方法来设计控制器。随着数字控制技术的发展,计算速度与计算精度已不会约束控制算法的实现[11],采用非线性补偿技术实现全局线性化成为可能,可以有效解决控制器在全局范围内性能不一致的问题。因此,本文采用这种方法实现全局线性化设计,并通过仿真分析延时环节等效为一阶惯性环节的限制条件,为控制器PI参数的选型提供依据。
1 大功率晶闸管整流系统结构

图1 大功率晶闸管整流系统结构图
图1 是大功率晶闸管整流系统的结构图。系统主要由高压部分、整流变压器、晶闸管整流器、无功补偿装置等组成。高压部分包括高压电网和高压开关柜。目前大功率晶闸管整流器有35kV、110kV、220kV这几种电压等级,且在往330kV及以上电压方向发展。
整流变压器用于将高压电网电压变换成整流装置所需的电压,并调整相位角以满足网侧和阀侧的运行要求[12]。常用晶闸管整流电路主要有双反星和三相桥两种[13]。三相桥电路主要应用于高电压场合,双反星电路一般应用在低压大电流场合。
图2为晶闸管整流器的控制器框图。本文采用的晶闸管整流控制器是以TMS320F28335为核心的双通道全数字控制结构,控制器A、B两通道互为热备冗余,当主通道出现故障时,备用通道自动无扰切换,以保证系统的可靠性和可用性。电流闭环控制算法由DSP软件实现,通过控制导通角,控制输出直流电压。同时,可根据客户不同的需求,增加无功补偿装置进行谐波滤波和无功补偿。

图2 大功率晶闸管整流器基本控制原理框图
2 大功率晶闸管整流的控制技术
2.1 全局非线性补偿方法
下面以三相全控桥式整流电路为例来进行分析。晶闸管控制角α与整流器直流输出平均电压Ud(α)的关系见式(1)[14-15]。

式中,Urms为阀侧相电压有效值。
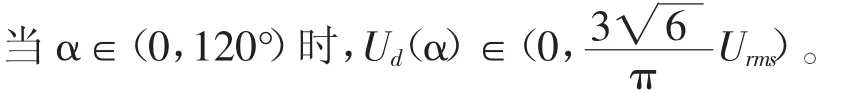
根据式(1)可得控制角α与直流输出电压Ud的关系见图3(a),控制角与输出电压关系图见图3(b)。直流输出电压与控制角之间不是线性关系,需要线性化之后才可使用控制器进行控制。文献[10]通过选定两个参考工作点,对直流平均电压Ud(α)和控制角α之间关系式进行泰勒展开,取其前两项,忽略高阶项,进行局部线性化。

图3 控制角与输出电压的关系
图4 (a)为采用控制角α直接控制的控制框图。此过程为非线性,本文构造一个新的函数α(β),见图4(b),使得当β均匀变化时,Ud也跟随它均匀变化,见图 4(c)。

图4 非线性补偿过程
根据以上分析,定义:

式中 β∈(0,120°)。


2.2 线性补偿系统建模与控制
在三相电路整流控制系统的动态过程中,由于晶闸管是半控器件,其导通后,需要受到反向电压作用才能截止,控制触发信号的改变并不会立刻起作用。这一短时失控相当于一个延时环节,其对应的传递函数为[10]:

在进行控制器设计时,将其等效为一阶惯性环节:

目前对失控时间Td的取法大致有两种,一种是每个周期控制一次脉冲触发信号,此时Td=20 ms。另一种是按每个波头控制一次脉冲触发信号,此时Td=3.33 ms。
3 仿真与分析
延时环节在低频时段可以等效为惯性环节,在高频时段,延时环节是不稳定,发散的。因此,将延时环节等效为惯性环节设计出的PI参数,在延时环节是否适用,需要进行仿真验证。
延时环节的系统控制框图见图5。

图5 延时环节系统控制框图
通过将其等效为惯性环节,可求得闭环传递函数为:

简单起见,只考虑临界阻尼的情况,即ξ=1,此时有,kp=2Tdωn-1,ki=Tdωn2。
在Td=20 ms和Td=3.33 ms时,取不同的ωn进行仿真,延时环节的仿真结果分别见图 6(a)、(b)、(c)和图 7(a)、(b)、(c)。

图6 Td=20 ms时延迟环节仿真结果波形图

图7 Td=3.33 ms时延迟环节仿真结果波形图
由图6可得,对于 Td=20 ms,当 ωn=25~33 rad/s时,kp=0~0.32,ki=12.5~21.78,此时延时环节近似等于惯性环节,系统稳定运行。当ωn<25 rad/s时,系统仍可稳定运行,只是不是最小相位系统;当ωn>33 rad/s时,延环节不受控,波形发散,系统不稳定。故kp的实际可取值范围为0~0.32,ki的实际可取值范围为12.5~21.78。由图7可得,对于Td=3.33 ms,当ωn=151.51~235 rad/s 时,kp=0~0.551,ki=75.75~182.24,此时延时环节近似等于惯性环节,系统稳定运行。当ωn<151.51 rad/s时,系统仍可稳定运行,只是不是最小相位系统;当ωn>235 rad/s时,延时环节不受控,波形发散,系统不稳定。故kp的实际可取值范围为 0~0.551,ki的实际可取值范围为 75.75 ~182.24。从上述分析可得到,在Td=3.33 ms时,ωn=151.51~235 rad/s,系统稳定,频带较大,动态响应快。
4 结语
晶闸管整流系统是一个非线性系统,这会约束其全局性能及动态响应特性,本文通过非线性补偿技术进行全局线性化,使得控制角与直流输出平均电压呈线性变化,有效解决了控制器在全局范围内性能不一致的问题。同时通过仿真实验,得到了延时环节近似等效为一阶惯性环节时、的取值范围,同时验证了当时,系统频带更宽,动态响应更快。
