瞬态瑞雷面波法检测路基填筑质量的定量分析

李炳秀 何明峰

(中国铁路设计集团有限公司，天津 300142)

1 概述

铁路路基填筑质量对铁路运输安全至关重要。目前常用的路基填筑质量检测方法，如环刀法、灌砂法、静载荷试验等，是随机检测单个点上的压实度和地基系数，很难对路基进行普查，而且随机采样的检测结果往往缺乏代表性。瑞雷面波法能够无损快速地对铁路路基填筑质量进行连续检测，克服了传统路基检测方法的不足。然而瑞雷面波法求得的各层瑞雷波速值只能说明填筑各层的软硬程度和填筑强度的均匀性，无法定量评价路基填筑质量。因此，求解瑞雷波速和压实度、地基系数的相关性，实现瑞雷面波法检测的定量分析具有十分重要的意义。

瑞雷面波最早由Rayleigh[1]在计算半空间自由界面中的平面波传播时发现。Haskell[2]计算出了瑞雷面波在不同介质中的频散特性，给出了对应的频散曲线。Hesisey等[3]提出了瞬态瑞雷面波法的频率域分析方法，进一步推进了瑞雷面波法的理论研究。1996年，刘云侦等[4]自主研制了SWS瞬态面波多道数据采集处理系统。卢宁等[5]应用瑞雷面波法检测公路路堤的填方量并取得了一定成果。范跃武等[6]利用τ-p变换来有效提取采集数据中的面波反射，并应用瑞雷面波法检测路基密实度。李海[7]讨论了瑞雷波速与路基承载力之间的关系，并给出了两者的相关性公式。李青山等[8]通过建立数学模型分析讨论瑞雷波速与压实度的相关性。董海文等[9]计算了瑞雷波速与压实度的回归经验公式。上官位等[10]通过分析瑞雷波速度与动力触探和静载结果，给出了路基承载力和瑞雷波速的线性相关公式。林向东[11]将BP人工神经网络模型应用在瑞雷面波法检测中，通过网络学习训练来快速计算波速值所对应的压实度。刘晓敏[12]对比分析了瑞雷面波法检测结果和灌砂法测试结果，确定了瑞雷波法检测路基压实度的可行性。刘超英等[13]通过对比分析瞬态瑞雷波速值和现场钻孔取样室内填筑材料的干密度试验资料，建立了瑞雷波波速与干密度的相关关系。

以下分析瑞雷波速与路基填筑干密度、地基系数的相关关系，给出拟合瑞雷波速与干密度、地基系数的数学回归公式，并结合工程实例计算在满足压实度(或孔隙率)和地基系数设计要求下所需要达到的最小瑞雷波速值。通过上述回归分析的过程，实现了瞬态瑞雷面波法的定量分析，解决了以往瑞雷面波法无法定量评价路基质量的问题。另外，将相关数学公式编入Excel表格，使其能够自动计算出瑞雷面波的数学回归公式和最小瑞雷波速，方便了实际工程应用。

2 基本原理

地震波分为两类，即体波和面波[14]，体波包括纵波(P波)和横波(S波)。当介质中存在分界面时，体波在一定条件下会相互干涉并迭加产生出一种频率较低、能量较强的次生波，因其主要沿介质的分界面传播，故称为面波。面波分为两类，即瑞雷波和勒夫波。

当在各向均匀介质中传播时，瑞雷波速与介质的物理力学性质有关，与频率无关。当在水平分层介质中传播时，瑞雷波速除与介质性质有关，还随频率的变化而改变，表现出频散特性[15]。不同频率的瑞雷面波传播深度不同，可根据瑞雷面波的频散特性划分层位并计算各层的瑞雷波速值。瑞雷波速与介质性质存在相关性，可根据计算出的瑞雷波速值反演各层介质的物理力学参数(压实度和地基系数)，从而实现路基填筑质量的定量评价。

在瞬态瑞雷面波法检测中，震源激发产生一个包含一定频率范围的瞬态激励，某接收点记录到的瑞雷面波有如下所示的频谱形式

(1)

其中，f1(t)是时间域波形函数，F1(ω)是频谱，ω是圆频率。

与该接收点相距ΔX距离的另一接收点记录到的瑞雷面波频谱F2(ω)为

(2)

其中，f2(t)是该接收点记录到的时间域波形函数。两接收点频谱间存在下列关系式

(3)

其中，VR(ω)是圆频率为ω时瑞雷面波的相速度。

公式(3)可写为如下相位差表示的形式

F2(ω)=F1(ω)e-iφ

(4)

其中，φ是F1(ω)和F2(ω)的相位差。根据公式(3)和公式(4)，有

(5)

即

(6)

公式(6)表明，已知两个接收点的距离和每个频率的相位差，便可以计算出每个频率的相速度。对单个接收点，分别计算出不同频率对应的速度值，就可以得到频率速度曲线，即频散曲线。

对多通道瑞雷面波法检测，瑞雷波速可写为

(7)

或

(8)

其中，VR是瑞雷波速，Δx是检波器道间距，Δt是相邻检波器接收到面波的时间差，f是频率，Δφ是相位差，N+1是检波器个数。公式(8)表明瑞雷波速与频率有关，通过反演VR-f曲线，即频散曲线，可以得到不同深度下的瑞雷波速。

频散曲线的反演建立在弹性波理论的基础上。根据弹性波理论，瑞雷面波的能量主要集中在一个面波波长深度范围内，而半波长理论表明，瑞雷波平均速度反映的是半波长深度处介质的平均弹性性质，故瑞雷波速和勘探深度有如下关系

(9)

其中，H是勘探深度，λ是面波波长。

根据公式(9)，可将频散曲线转换为深度速度曲线，可得到该接收点处不同深度介质的瑞雷波速值。

瑞雷波与介质性质的相关性可由剪切波进行推导。由弹性力学公式可知

(10)

其中，VS是剪切波速，G是剪切模量，ρ是密度。

在等效半空间条件下，瑞雷波速VR与剪切波速VS有如下关系式

(11)

其中，μ为地层泊松比，对于常用的铁路路基填筑土体，可以近似认为瑞雷波速等于剪切波速，即

(12)

剪切模量G与弹性模量E间存在如下正比关系

G=αE

(13)

其中，α是比例系数(α≤1)，当土的密度增加时，α接近于1。对特定介质，α为常数。

根据地基系数K30的计算公式

E=0.79(1-μ2)DK30

(14)

其中，D是荷载板直径。联立公式(12)到公式(14)，推导出瑞雷波速和地基系数的相关公式为

(15)

目前，国内外关于密度与瑞雷波速关系的研究表明，两者之间存在以下幂函数关系式

(16)

其中，A和B为函数系数，对特定介质为常数。将公式(16)代入公式(15)可知，地基系数与瑞雷波速的幂指数成正比关系，即

(17)

其中，

(18)

对特定介质，A，B，μ，D，和α均为常数，所以a和b也是常数。

压实度K的计算公式[16]为

(19)

其中，ρ0是最大干密度，对特定介质为常数。将公式(16)代入公式(19)，压实度K与瑞雷波速VR也有如下幂函数形式的关系式

(20)

其中，c和d是函数系数。公式(17)和公式(20)表明，压实度和地基系数与瑞雷波速的幂函数存在正比关系，这一关系式是进行瑞雷波法定量分析的理论基础。在实际工程应用中，由于路基填料的性质变化较大，土体模型并不满足理想的等效半空间各项同性介质的条件。为此，在理论公式的基础上，利用试验数据的回归分析来确定最佳拟合参数，并计算在符合路基填筑设计标准下所需的最小瑞雷波速。

对含有两个未知数的幂函数方程，当要拟合的数据点大于两个时，回归过程可写为如下所示的超定方程组

(21)

其中，y代表压实度或地基系数，x代表瑞雷波速，n是要拟合的数据点个数(n为整数且n>2)，a和b是待求拟合参数。公式(21)中方程个数大于未知数个数，方程组超定，常用的求解方法是在最小二乘意义下进行非线性拟合，即求取满足目标函数时a和b的值

(22)

求出a和b后，将设计参数要求的最小压实度或地基系数代入幂函数回归方程，即可得到对应的最小瑞雷波速。

3 工程实例

根据某铁路路基基床表层的瑞雷面波、干密度、和地基系数采集数据，分别计算瑞雷波速与干密度、地基系数的幂函数回归方程，并用拟合误差和相关系数来验证回归拟合的准确性。最后，根据该段铁路路基的设计参数要求，利用回归方程预测出满足设计要求的最小瑞雷波速。所有计算过程被编入Excel表，以方便实际工程应用。

该段铁路路基基床表层分别采用灌砂法、K30和瑞雷面波法进行检测。瑞雷面波法配套仪器为国产SWS-6工程勘探与工程检测仪。根据该段路基的测试段落长度，选择测点间距为5 m。每个测点使用12道4 Hz低频检波器采集信号，采样间隔0.1 ms，记录长度200 ms，道间距1.0 m，偏移距2.0 m。采用50 kg级落锤锤击垫板作为单边激发震源，每个测点重复检测一次。

得到瑞雷面波数据后，可以通过一系列数据处理得到每个测点处的瑞雷波速。首先，在时间距离(X-T)域设置面波时距窗口和频率范围，保留时窗中的有效信号并去除时窗外的干扰信号。其次，将X-T域中的瑞雷面波数据通过傅里叶变换转换到频率波数(F-K)域。在F-K域选定基阶面波的能量峰脊，计算出不同频率对应的瑞雷波速，画出频散曲线。根据得到的频散数据以及频率与面波勘探深度的关系式，在设置初始地层参数后，经过人机联作，优化拟合，将频散曲线转换为深度速度(Z-V)曲线，得到在深度速度(Z-V)域的瑞雷面波数据，从而计算出采集排列测点下方介质瑞雷波速的分层断面和基床表层各位置的瑞雷波速值。

干密度和对应测点处瑞雷波速数据如表1所示。

根据公式(16)和表1的数据，利用最小二乘法非线性拟合，建立干密度与瑞雷波速的回归方程

(23)

回归方程的相关系数为0.953，其回归曲线如图1所示。

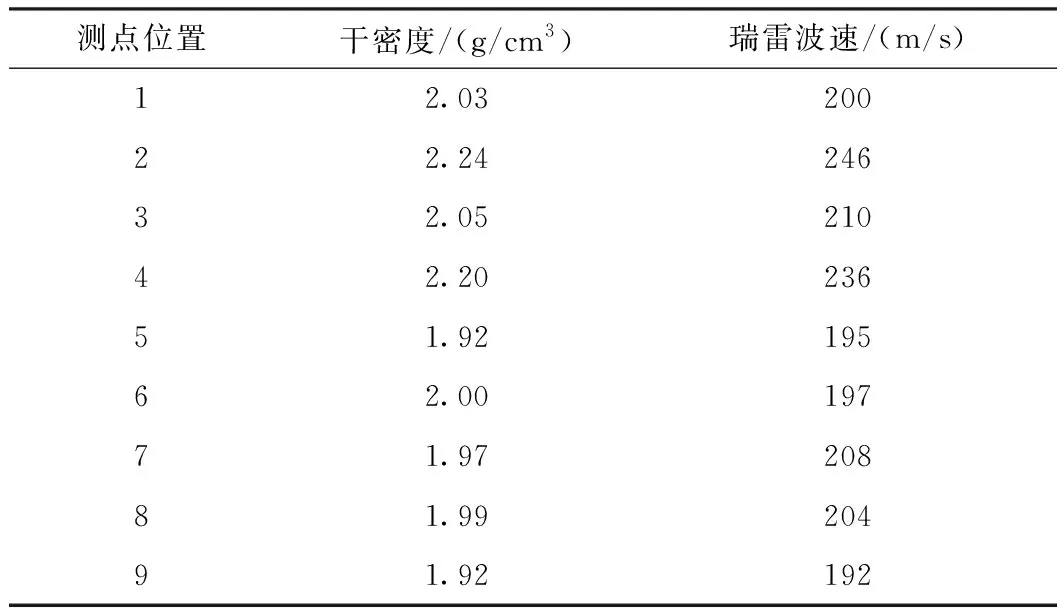
表1 干密度和瑞雷波速数据

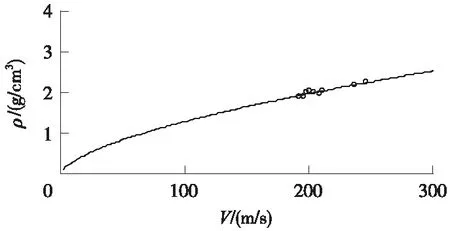
图1 干密度与瑞雷波速回归曲线

利用公式(23)和瑞雷波速反算干密度，如表2所示。

表2表明，公式(23)的平均拟合误差为1%，最大拟合误差不大于2.5%。另外，其相关系数大于95%，证明了回归方程的准确性。

表2 干密度和反算干密度对比

该段铁路路基基床表层使用的是A组填料，设计参数为孔隙率小于等于31%，土的颗粒密度为2.71 g/cm3。为求出满足设计参数要求的最小瑞雷波速，首先根据孔隙率计算公式求得当孔隙率等于31%时，干密度为1.87 g/cm3。然后将该干密度值代入公式(23)，求得对应的瑞雷波速为182 m/s。该瑞雷波速值即是满足设计参数要求的最小瑞雷波速，当路基基床表层瑞雷波速大于等于182 m/s时，即可视为该处路基填筑满足设计的最大孔隙率要求。

下面推导地基系数与瑞雷波速的关系式。在删除偏差较大的采集数据后，该段铁路路基基床表层地基系数和瑞雷面波法检测数据如表3所示。

表3 地基系数和瑞雷波速数据

根据公式(17)和表3的数据，利用最小二乘法非线性拟合，建立地基系数与瑞雷波速的回归方程

(24)

回归方程的相关系数为0.995，其回归曲线如图2所示。

图2 地基系数与瑞雷波速回归曲线

利用公式(24)和瑞雷波速反算地基系数，如表4所示。

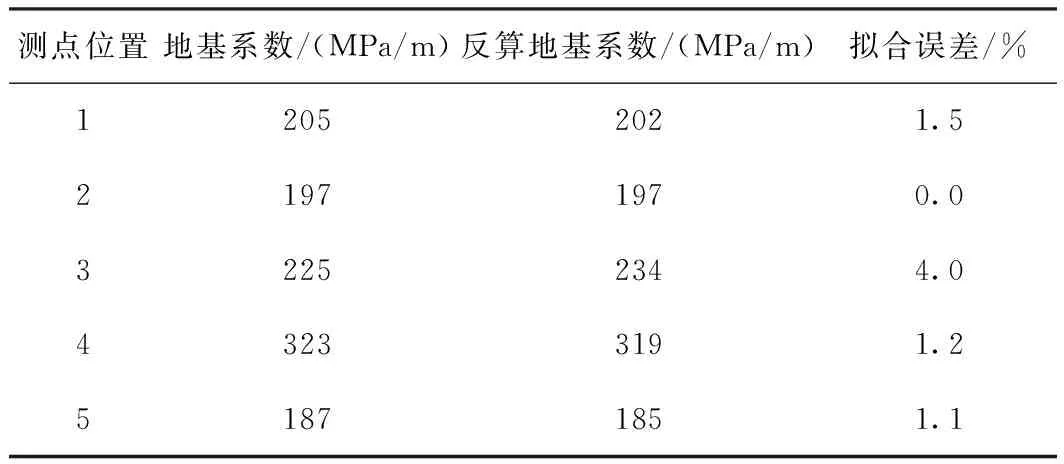
表4 地基系数和反算地基系数对比

由表4可知，公式(24)的平均拟合误差为1.56%，最大拟合误差不大于4%。另外，其相关系数大于99%，证明了回归方程的准确性。该段铁路路基基床表层设计地基系数大于等于120 MPa/m，将其代入公式(24)，求得对应的瑞雷波速为145 m/s，即当路基基床表层瑞雷波速大于等于145 m/s时，该处路基填筑满足设计的最小地基系数要求。

为方便实际工程应用，将上述计算过程编入Excel表格，对不同地区和填料的路基，使用时只需将采集的瑞雷波速、干密度(或压实度)和地基系数填入表格，即可自动求出该段路基在满足设计要求条件下的最小瑞雷波速，实现瑞雷面波法的定量分析评价。回归分析时用到的数据量越大，数据偏差就越小，最后得到的结果越准确。

4 结论

瞬态瑞雷面波法能够实现路基填筑质量的无损快速连续检测，面波法只能检测出路基软硬程度，无法对路基填筑质量进行定量评价。本文提供了一种定量分析方法，并通过工程实例进行验证，得到以下结论：

(1)给定压实度和地基系数的设计值，利用二者与瑞雷波速的回归方程可以计算出相应的瑞雷波速设计值，即当瑞雷波速大于等于该值时路基填筑质量合格。由此解决了以往瑞雷面波法只能定性判断路基填筑软弱夹层的缺陷，实现了瑞雷面波法对路基填筑质量的定量分析，简化了路基填筑质量的检测过程。

(2)理论推导表明，幂函数形式的回归方程是瑞雷波速与干密度、地基系数的最佳拟合函数。工程实例进一步验证了幂函数回归方程具有较大的相关系数和较小的拟合误差，证明了回归方程的准确性。

(3)最小二乘法非线性拟合是求解幂函数回归方程的最优化数学方法，拟合用的数据越多，求出的回归方程准确度越高。

(4)求出回归方程后，将干密度和地基系数的设计参数代入回归方程，求出满足设计要求的最小瑞雷波速，可为瞬态瑞雷面波法的定量分析提供评价标准。