柔性淹没植被河道水流结构研究与进展

陈甜甜，赵明登，张 颖

(武汉大学水利水电学院，武汉430072)

0 引 言

恢复河道水流生态功能，已成为当前河流治理、水生态保护与修复的重要目标[1]，旨在强调生态系统的活力、稳定性能、自我调节能力等生态系统中人与自然的和谐共处[2]。河流生态系统是自然界中重要的生态系统之一，具有排涝、供水、生态、发电、航运、景观等多重功能。而水生植被作为河流生态系统中不可或缺的部分，一方面可以增大水流的阻力，增加水流内部结构的复杂性，进而加大河床演变及污染物输移等的预测难度；另一方面可以有效改善水质，为水生生物提供良好的栖息地，有助于增加生物的多样化。同时利用水生植被净化功能修复污染较为严重河道，利用根茎的吸附固定作用守滩固沙并稳定河势，都有助于水生态环境的保护和修复。水污染及洪涝灾害日趋严重，对河道水流的深入研究已迫在眉睫。

近年来，随着经济的飞速发展，越来越多的城市重视生态河流的建设。柔性淹没植被作为水生植被的典型代表，具有极高的生态服务价值。柔性淹没植被(见图1)是指根茎扎入泥中，整个植被淹没在水中，且受水流作用容易发生弯曲、倾斜及摆动的植被(狐尾藻、金鱼藻、黑藻属等)。以往研究多以实验为手段，主要探索了植被河道中植被阻力特性、流速分布规律和紊流特性，以及植被水流中物质输移、吸收、扩散等规律。探索柔性淹没植被的水动力学特性、水流阻力特性、水流内部结构，对于植被护坡固土、改善水质及治理河水污染等生态型河道的设计和管理具有重要的工程意义和社会经济效益。

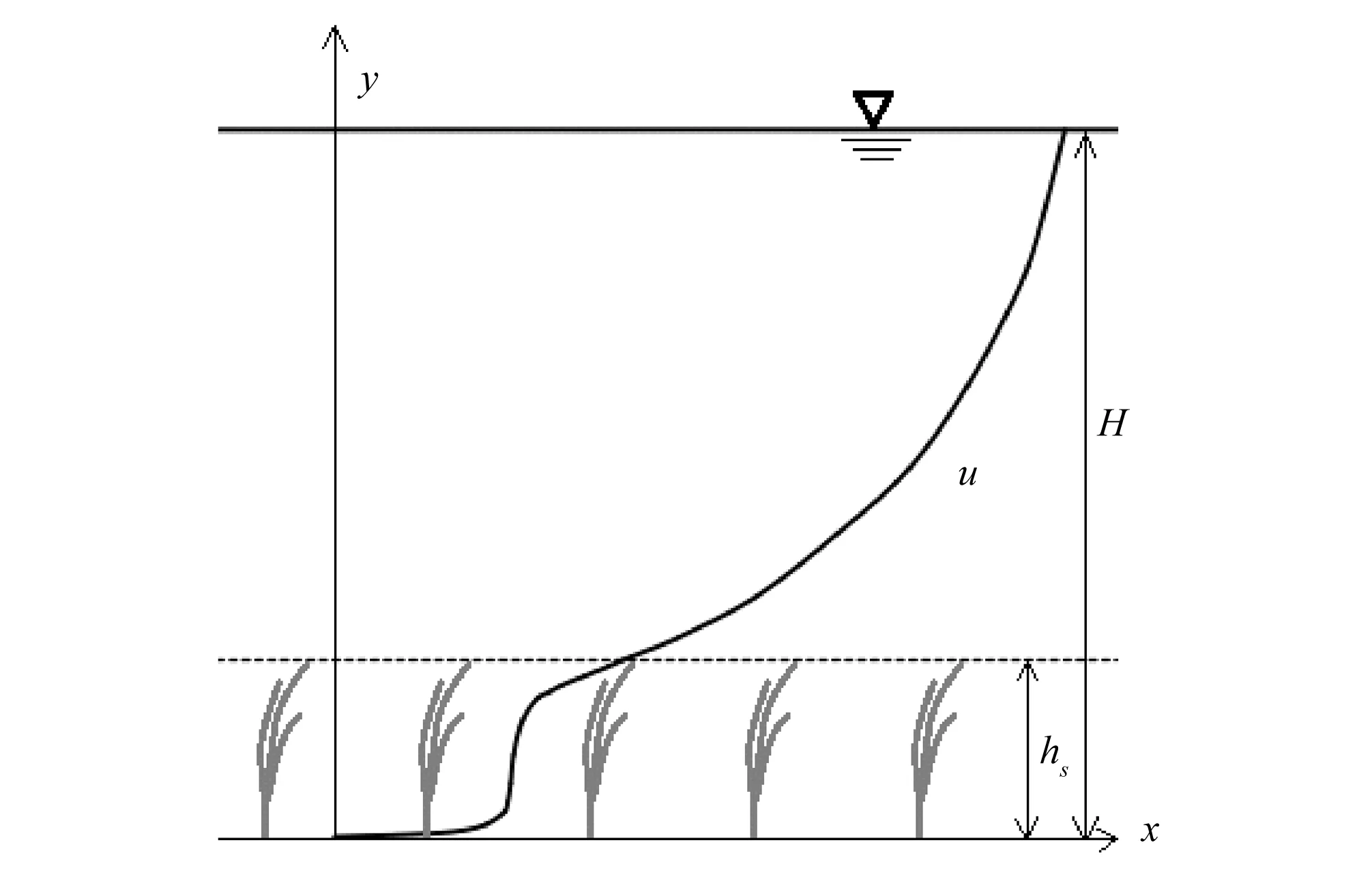
图1 柔性淹没植被水流运动示意图

1 柔性淹没植被河道水流理论与实验研究

1.1 柔性淹没植被水流阻力特性

在河道行洪设计安全过程中，含植被河道阻力机制是不可忽视的因素之一。水流阻力主要来自三个部分：水流流经植被所引起的植被阻力、无滑移边界所引起的边壁阻力及边界突变所引起的局部阻力，其中植被阻力占主要部分。国内外学者针对曼宁糙率系数n和阻力系数Cd进行了大量研究[3-5]。

在水流的作用下，柔性植被会有一定程度的弯曲变形、随流摆动，因此影响植被水流的水动力因素会更加复杂。Cook&Compbell[6]在1939年指出在低速水流情况下草会出现“摆动”。Ree&Palmer[7]进一步指出，植被发生摆动后，整体均匀化，像被梳子整理过，因此含柔性植物河道水流实际上是一个动边界问题。

1.1.1 针对曼宁糙率系数的分析研究

Chow[8]总结了影响曼宁糙率系数的十种因素：水位、水量、季节改变引起的植被变化、渠道大小及形状、渠道不规则程度、渠道冲淤情况、渠道悬浮物和底泥种类、渠道转弯半径、渠道表面粗糙度、渠道水工建筑物的建设情况，绘制了曼宁糙率系数与雷诺数之间的关系曲线，即n～VR曲线，提出在淹没状态下，n随着VR的增大而减小。

n～VR曲线的不足之处在于没有考虑植被的变形(弯曲与倾斜)。Kouwen[9]发现当河道坡度小于5%、植物韧度较高或植物为单一特定时，这一曲线并不适用。Kouwen认为柔性植物对水流的阻力作用还要受到植物本身的形状及水流流态的制约，提出单位面积上植被的抗弯刚度理念(MEI)，并给出曼宁糙率系数半经验公式：

(1)

式中：H为水深；C0和C1分别反映植被刚度、偏转特性的经验系数；hs为植被弯曲后的高度。

考虑到曼宁糙率系数的复杂性，也有部分学者针对糙率系数的影响因子展开研究。Velasco等[10]对不同密度柔性淹没植被进行试验研究，结果表明：植被糙率与高度偏移值有直接关系；相对糙率与流量呈负相关，其阻力系数趋于某一特定值。吴福生[11,12]将淹没状态下柔性植被阻力特性与刚性植被进行对比，发现随着植被密度的增大，糙率系数增大；对于特定植被密度，糙率系数随着相对深度H/hs的增大而减小。姬昌辉[13]认为在一定水深条件下，水流流速变化对糙率的影响较小，可以忽略，从而建立了计算糙率系数的无因次经验公式：

(2)

式中：d为水草的截面直径；L为水草的间距；h为水草的高度。植被淹没度、水流流速与植被水流阻力的定量关系仍需进一步研究。

1.1.2 针对植被阻力系数的分析研究

Järvelä[14]研究天然湿地和河漫滩中植被水流阻力特性，以莎草、小麦、柳叶状天然混合草为对象，开展典型低速流试验，发现该成果适用于水力坡降小的区域。Petryk[15]通过研究植被群体阻力，提出单位长度内河道动量平衡公式：

ρgAS0=D+τ0P

(3)

式中：ρ为水体密度；A为过水断面面积；S0为河道底坡；D为植被阻力；τ0为边界剪切力；P为湿周。

在水流定量平衡模型的基础上，后续学者进行相关扩展。Carollo[16]收集相关试验数据后，推导出有关植被阻力与剪切雷诺数、相对植被高度和植被弯曲度的关联方程。Järvelä[17]在矩形渠道中进行淹没柔性植被水槽试验，并探讨植被对水流的阻力和水流结构的影响规律。Dunn等[18]、Wilson[19]、胡旭跃[20]、Zhu等[21]采用柔性模拟材料，进行了淹没和非淹没两种情况下的模拟实验，发现影响阻力系数的因素主要有流量、水流雷诺数及柔性植被力学特性(植被淹没深度、密度、柔韧度等)。

从柔性淹没植被水流阻力特性研究进展来看，国外研究主要涉及植被阻力的机理与特性方面，国内研究侧重于植被力学特性、流量和水流雷诺数等对水流阻力的影响，对曼宁糙率系数和植被阻力系数研究仍有待深入。

1.2 柔性淹没植被水流纵向流速分布

纵向流速分布情况是柔性淹没植被河道过流能力预测的重要指标，其分布与植被形状、植被密度、水深等因素密切相关。国内外多数研究者通过简化动量平衡方程或者提出新的紊流模型，对比室内水槽试验数据，推出流速分布公式[22-24]。

根据柔性淹没植被河道纵向流速的区域变化特性，学者们通常将区域划分为2～4个。Yang和Choi[25]提出了明渠淹没植被的两层模型，假定植被层内平均流速均匀分布、植被上层符合对数律分布。王莹莹[26]根据模型试验结果，划分为 3个区域，纵向流速垂向上单调递增，达到某个值趋于稳定，之后为半对数分布。Nikora[27]提出了一种求解流速沿整个水深分布的新方法，他认为淹没植被水流流速主要由四部分线性叠加构成，①近壁区域植被底层的流速为均匀分布；②植被顶部附近混合层流速为双曲正切分布；③自由水层边界层为对数分布；④植被影响下的尾流函数。区域的划分会根据植被类型、试验布置、水流流态等不同而发生变化。

基于分区模型，后继学者发现纵向流速主要取决于植被形态特征、柔韧度和水流流态等因素。槐文信等[28,29]在进行一系列柔性淹没植被明渠水流试验研究后，发现植被上层区域纵向流速呈对数律分布，植被区域纵向流速呈S型分布；提出用河道压缩参数描述植被对水流的影响，并给出一个新的混合长度公式。吴福生[11]采用PVC薄片模拟柔性植被，用标准PIV(粒子图像流速仪)观测不同位置的流速场，分析发现植被冠层以下区域，流速明显减小，随着流量的增加，植被对纵向流速的影响范围减少；植被冠层处，流量和植被密度的增加都会加大流速梯度。杨婕等[30]采用定床阻力试验模拟植被覆盖下的水流流动，结果表明：柔性植被覆盖下，水流平均流速随流量增大而增大。

1.3 柔性淹没植被水流紊动结构特性

柔性淹没植被可改变河道水流的紊动结构，对河道中物质输移和泥沙运动影响很大。Nikora[31]认为柔性淹没植被水流中存在六种尺度紊动结构，一是水深尺度的由剪切产生边界层紊动，以植被层为新床面且位于植被上方的流速满足对数律分布；二是由Kelvin-Helmholtz不稳定性产生的植被尺度紊动，位于植被顶部；三是植被叶片尺度的边界层紊动；四是叶片尺度的混合层紊动；五是茎干尺度的尾流紊动；六是由植被摆动产生的紊动。紊流强度及雷诺应力呈各向异性[32]，并且紊动强度和雷诺应力最大值发生在淹没植被冠层交界处[33,34]。李艳红等[35]建立淹没植被水流紊动强度经验公式，认为紊动强度最大值与植被密度有关，紊动强度最大值的发生位置与水深比(弯曲植被冠层高度/水深)有关，断面平均流速对紊动强度最大值的大小和位置均有一定影响。

此外，吴福生[36]基于涡动力学观点，对淹没柔性植物水流二维垂直涡量场分布进行探索，研究发现：形成植物水流涡量关键因素是流速梯度；在植物冠层处，水流流速梯度大，能量耗散率也高。目前研究主要针对紊动强度和雷诺应力的垂向分布，尚未揭示紊流垂向交换与水平交换之间能量损失的定量关系。

2 柔性淹没植被河道水流数值模拟研究

数值模拟可以较为准确地模拟和预测整个计算区域水流特性，已成为工程设计和研究植被水流的重要工具。诸多学者利用模型计算的结果与试验值吻合, 以验证所采用的方法行之有效。植被水流数值模拟研究起步较晚，目前刚性植被水流的模拟较多，而有关柔性淹没植被的研究则相对较少。

描述植被流运动变化本质上是N-S方程组，但其非线性导致求解方程组尤为困难。而工程上人们关注的是总效、平均的作用，所以对方程组采取统计平均的办法，也就是时间平均(雷诺平均)的办法。目前常采用的紊流模型主要有标准 模型、雷诺应力模型、LES(大涡模拟)模型等，常用的软件主要有Flow 3D、Delft 3D、Fluent等。Ikeda和Yamada等人[37]在原来大涡模拟网格的基础上，引入植被网格的概念，采用二维LES技术对柔性植被水流进行了研究。LES模型能提供柔性植被冠层雷诺应力的各向异性，但需要的网格较为精细，模型也不能同时体现具有不同几何形态的河道水流流动。

Velasco等[38]人采用数值解法计算并分析河床上含柔性植被水流的纵向流速分布特点和紊动切应力分布规律。Li等[39]基于更精确的大挠度分析理论确定与水流速度有关的植被高度，用阻力系数和投影面积乘积的变化来表示叶子对流动阻力的影响，从而建立三维数学模型。Wu J等[40]提出了一种隐式IB-LB(浸入式边界-格子玻尔兹曼)耦合方法，很好地解决了显式IB-LB方法受时间步长和边界刚度不稳定性限制的问题，模拟的流场和叶片运动与PIV试验得到的结果一致，进一步验证了该方法的准确性。分析叶片参数对叶片振动特性的影响，结果表明叶片质量和弯曲刚度分别是影响振动幅度和振动频率的主要因素。目前柔性植被水流的动边界问题尚未得到很好的解决。

3 结论与展望

从理论分析、试验研究、数值模拟三个方面总结分析了柔性淹没植被水流结构研究和发展动态。柔性淹没植被水流特性需要采用分区研究，纵向流速沿垂向上的一般呈“S”形分布；植被阻力可以采用曼宁糙率系数或阻力系数的经验公式；紊动强度及雷诺应力具有各向异性，其最大值发生在淹没植被冠层交界处。由于柔性淹没植被水流的复杂性，许多问题有待进一步的研究与探索。

(1)柔性淹没植被在水流作用下会发生弯曲和摆动，植被的弯曲和摆动会改变水流的流动型态和阻力，因此柔性淹没植被与水流的相互作用机理需要进一步探究。随着数值模拟技术的发展，柔性淹没植被摆动所产生动边界问题可以更为深入地研究，以真实地反映植被水流流场，解决工程实际问题。

(2)曼宁阻力系数是基于恒定均匀流概念提出的，而实际水流多是在恒定非均匀流甚至非恒定流，因此除了水槽实验外，还应考虑实际河道、天然植被植被的水流阻力机制研究。

(3)河道中的柔性淹没植被水流运动属于多学科交叉问题，植被水流中常常有泥沙、污染物、生物等的输移和变化，因此需要进一步研究柔性植被对泥沙淤积及污染物输移特性的影响，利用水生植被对污染水体的修复净化，具有广阔的应用市场和前景。

□