基于MODFLOW的地下水动态变化特征分析
——以位山灌区为例
2018-08-29王艳茹徐征和
王艳茹,徐征和,王 通
(济南大学资源与环境学院,山东 济南 250022)
0 引 言
MODFLOW是模块化三维有限差分地下水流动模型(The modular finite difference groundwater flow model,简称MODFLOW),由美国地质调查局开发、用来模拟地下水流动和污染物迁移等特性的计算机程序。国内外学者利用其构建地下水系统模型,从多个方面和角度研究地下水系统动态演变规律。比如,Kapil K. Narula等人在对喜马拉雅流域研究的基础上,采用SWAT、MODFLOW和MT3DMS软件构建该流域的地下水系统模型,并研究分析在变化条件下地下水的演变规律[1]。在国内,娄华君等学者通过利用MODFLOW软件模拟分析并提出解决地下水超采造成的地质灾害的措施,为合理利用地下水资源提供科学依据[2]。综合看来,当前针对地下水系统动态演变规律的区域研究仍较为匮乏,位山灌区也不例外。
位山灌区地处山东省鲁西北平原,是黄河下游区域最大的引黄灌区。目前,仅吴传贵等人依据位山灌区地质勘查和实测地下水位等数据,分析农业灌溉和地下水开采对当地地下水补给、径流和排泄的影响[3]。综合来看,已有研究中尚未应用MODFLIW软件进行模型模拟,所涉及的数据空间过于单一,针对性较弱等问题,可见该区域相关研究尚显薄弱。本次研究以位山灌区作为研究对象,根据灌区地质、水文地质条件调查等相关资料分析,构建灌区浅层地下水系统数值模型,通过采用翔实的地下水动态监测资料等进行模型调参校准识别,基于校准验证后的数值模型对位山灌区现状地下水变化进行水均衡状态分析,为灌区地下水资源合理开发利用提供理论依据。
1 研究区概况
1.1 地理位置
位山灌区位于山东省聊城市境内,南临黄河,地处东经115°16′~116°30′、北纬35°47′~37°03′之间,总面积位0.54 万km2,其中设计灌溉面积为0.36 万km2。详见图1。
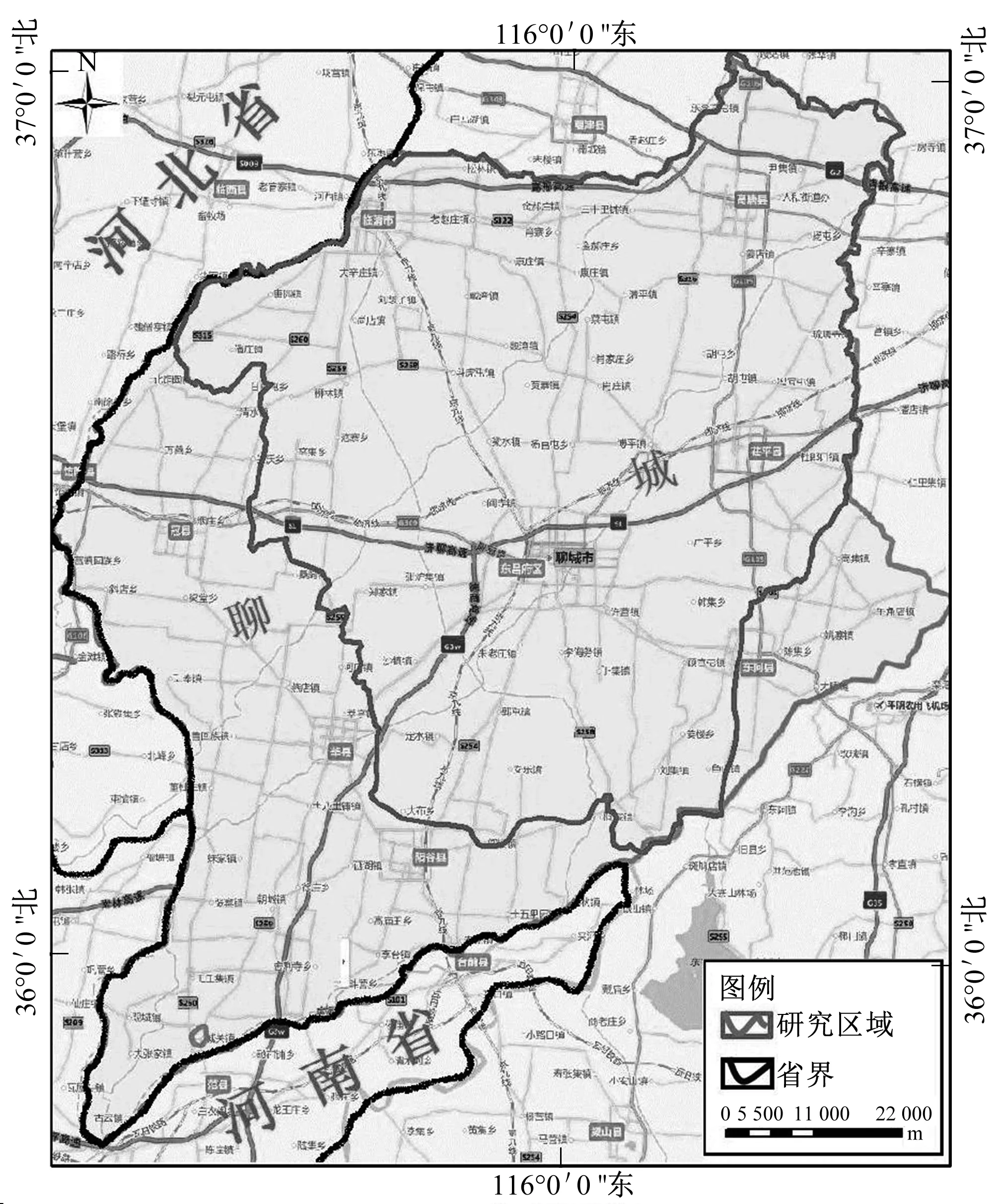
图1 研究区域地理位置图Fig.1 Location of study area
1.2 水文地质条件
位山灌区地属半干旱半湿润大陆性季风气候,四季变化明显,据调查可知,灌区年均降水量是548.7 mm;位山灌区位于海河流域,水资源主要是由大气降水、河流、地下水以及客水资源构成,根据统计资料灌区地下水资源总量为91 622.6 万m3,其现状年地下水开发利用量为59 985.1 万m3;位山灌区地处黄河冲淤积平原,地势变化幅度较小,灌区西南区域地势较高,东北区域地势较低,地表高程范围为28.99~34.88 m,地面自然坡降为1/7 500~1/10 000;位山灌区属于黄河下游鲁西北平原,在地质构造上地处中朝准地台,根据灌区地质资料可知区内相间分布有多种类型地质构造单元,详见图2。
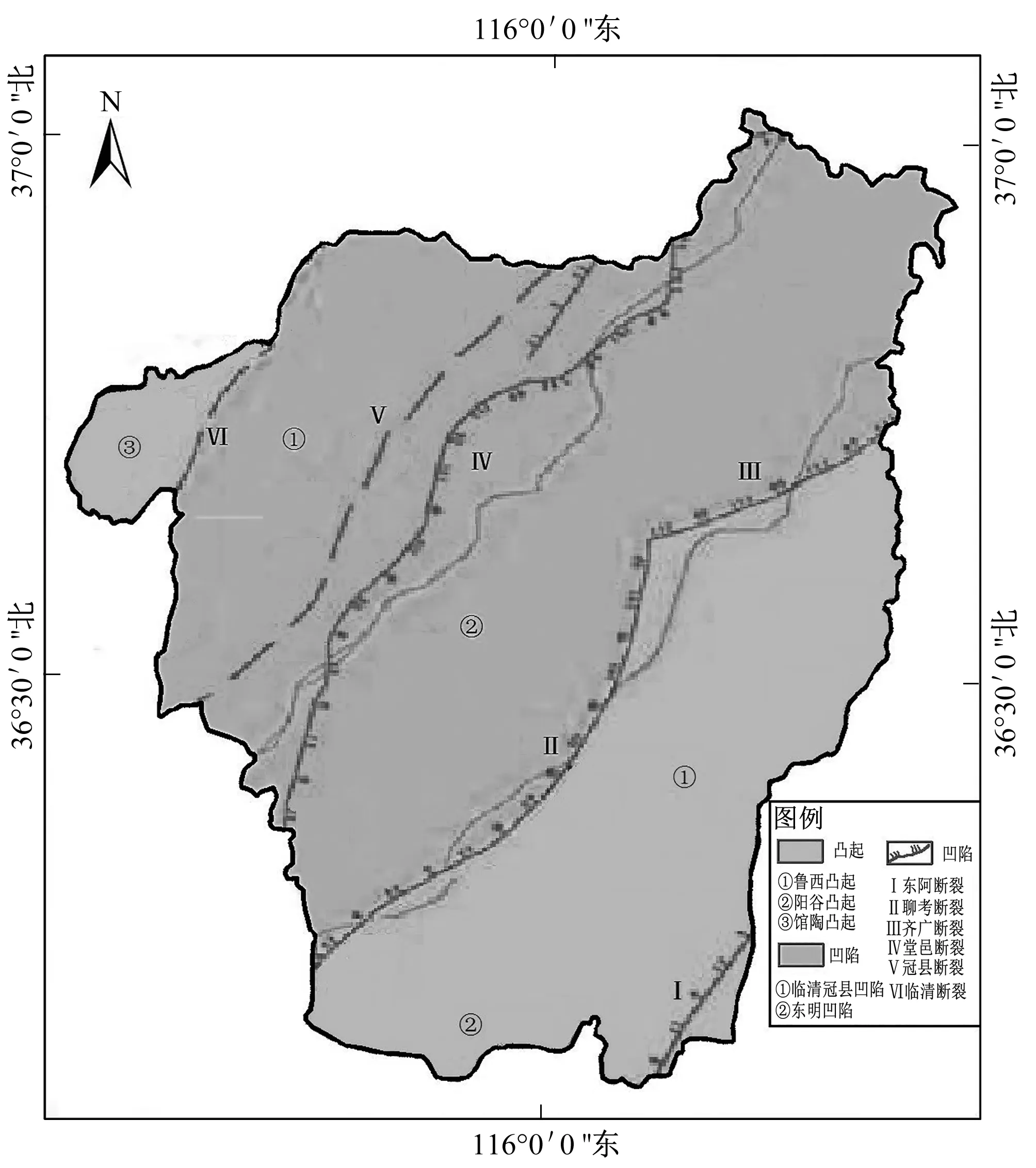
图2 位山灌区地质构造分布图Fig.2 Geologic structure distribution of study area
位山灌区地下水动态分析中的主要水文地质参数包括给水度、渗透系数等。
(1)给水度μ。本文通过地下水动态监测资料,并结合位山灌区有关实验研究成果确定了不同岩性的给水度,见表1。

表1 位山灌区给水度μ值表Tab.1 Specific yield μ of Weishan irrigation area
(2)渗透系数K。本文根据有关抽水试验和同位素示踪实验成果进行综合分析,确定了不同岩性的渗透系数K,见表2。

表2 位山灌区不同岩性K值表Tab.2 K of different lithology in Weishan irrigation area
根据以上水文地质参数范围,对位山灌区进行水文地质参数分区,见表3,图3。
2 研究方法
2.1 水文地质概念模型
(1)含水层的概化。根据灌区地质勘探资料和水文地质资料分析可知,灌区内含水介质的透水性具有空间分布特点,但是每处各方向行的渗透性能相同,因此将研究区域含水层系统概化为一层非均质、各向同性潜水含水层。依据灌区试验站提供的地下水水位、流场分布等相关资料可以将灌区地下水流场概化为服从渗流连续性方程和达西定律的平面流动。通过分析最终确定把研究区域浅层地下水系统概化为二维非稳定平面流运动模型。
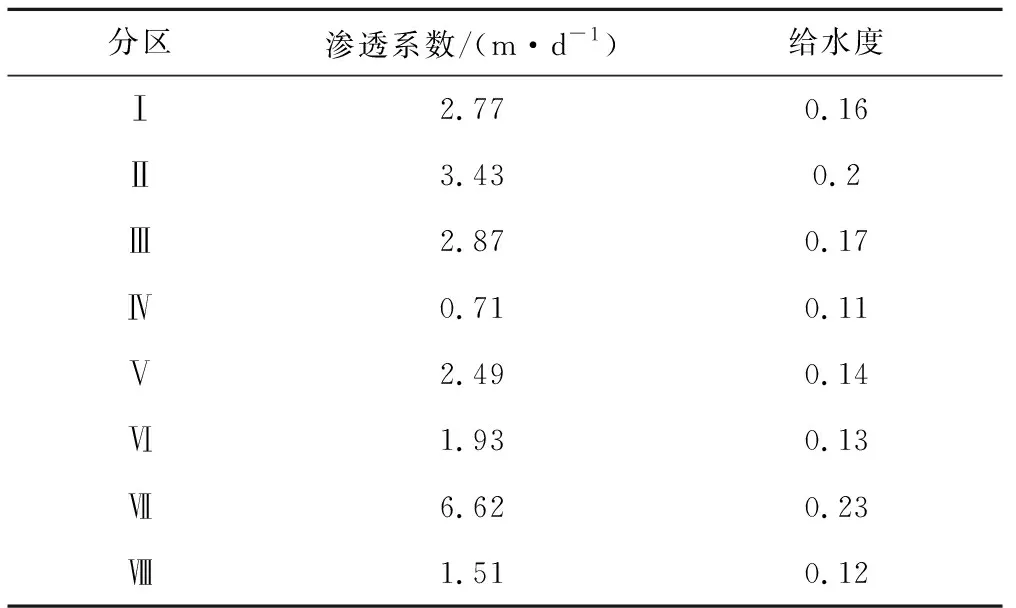
表3 位山灌区水文地质参数分区Tab.3 The Hydrogeological parameter zone of Weishan irrigation area
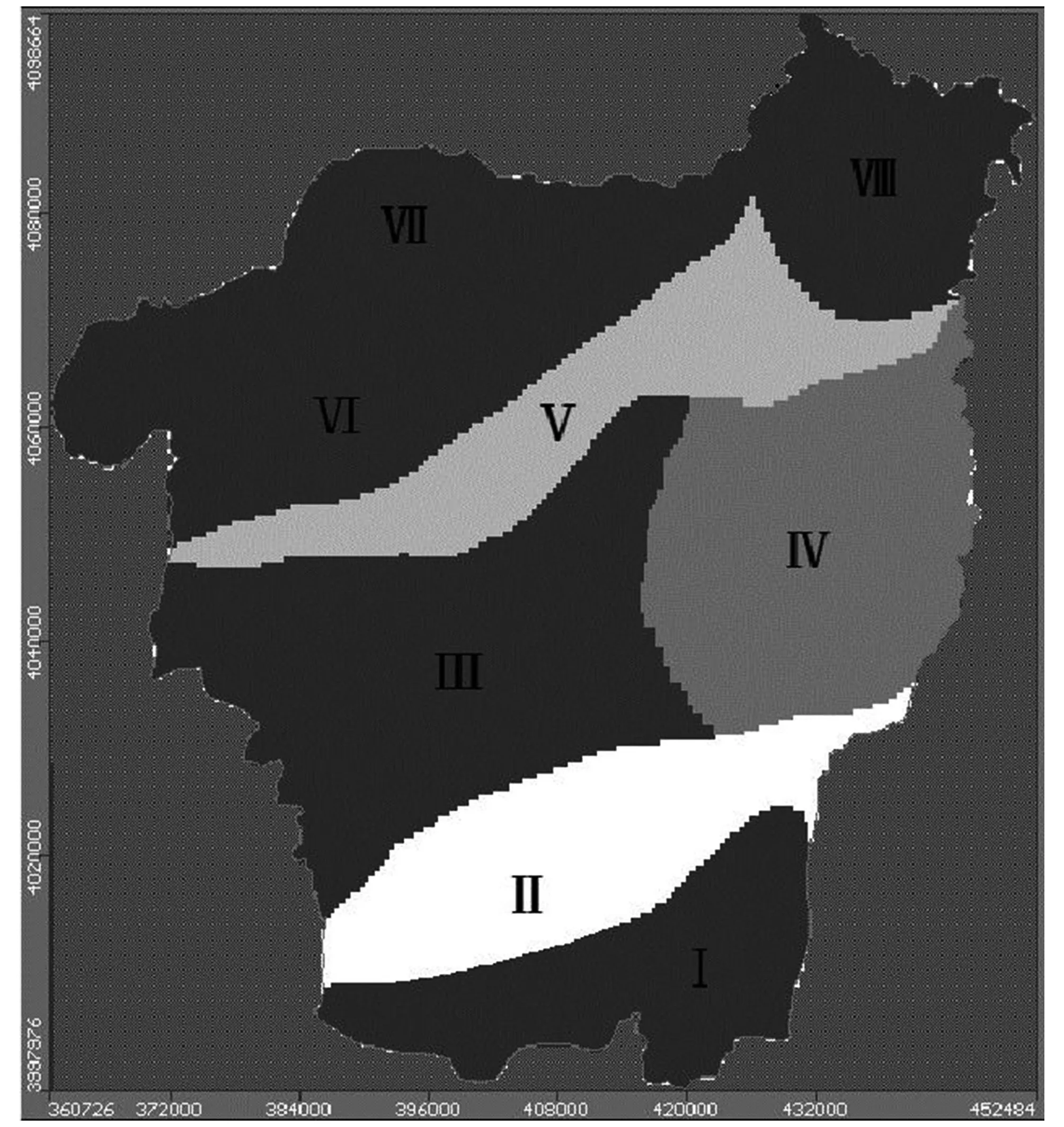
图3 位山灌区水文地质参数分区图Fig.3 The Hydrogeologic parameter zone of Weishan irrigation area
(2)边界概化。位山灌区的北部局部区域以卫河为边界,即从王庄电灌站到张官屯水库区域;而南部局部区域以黄河为边界,即从牛屯乡到鱼山乡区域,因此将该区域含水层沿河边界概化为第一类已知水头边界。依据位山灌区地下水流场分布特征将牛屯乡到王庄电灌站和鱼山乡到张官屯水库区域概化为第二类水头边界。灌区浅层地下水主要从灌区上部边界接受水量补给,依据模型概化原则将灌区上部区域概化为水量交换边界。通过水文地质资料可知灌区下边界为渗透性较差的黏土组成的隔水层,潜水下渗补给量较少,据此将该层概化为研究区域的隔水边界。
(3)水文地质参数和源汇项的处理。位山灌区的水文地质参数主要是由水文地质条件和抽水试验结果确定。根据灌区水文地质勘察报告和抽水试验资料,位山灌区的渗透系数为0.8~5.8 m/d,给水度为0.09~0.25。在建模过程中,根据水文地质条件给出参数初始值,通过水位拟合调整参数,确定各分区的水文参数值。
本次研究以灌区浅层地下水作为研究对象,源汇项是由补给和排泄两项构成。灌区浅层地下水主要接受降水和农业灌溉水下渗补给、河流渠道渗漏以及含水层侧向流入;而通过蒸散发、地下水开发利用以及含水层侧向流出等方式排泄。
2.2 数学模型的建立
按照地下水运动定律如质量守恒原理和达西定律等原理以及对位山灌区水文地质条件、渗透系数等相关参数和地下水流场进行科学系统分析,采用下述的偏微分方程组和边界条件表示前述已概化的位山灌区地下水流动系统。
(1)
式中:A为研究区域;x,y为空间坐标,m;k是渗透系数,m/d;S是饱和含水层的贮水系数,1/m;t是时间变量,d;h(x,y)是地下水待求水位,m;h(x,y)是初始水位,m;h1(x,y)是第一类边界水位,m;q(x,y,t)是第二类边界单宽流量,m3/d;n是第二类边界条件内法线方向的单位向量;S1,S2是第一类和第二类边界。
构建的地下水数学模型属于二阶非线性偏微分方程,在求解过程中需要先将待解方程转化为线性方程再求解。本文选用以有限差分法为基础求解方法的Visual MDFLOW软件进行数学模型求解。该软件可以根据研究区域不同区域功能进行模块化设置,有利于进行模型参数和边界条件等划分和设定。除此之外,软件自带多种解算器如PCG2、SIP、SOR等,可选择不同解算器进行地下水流动模型数值方程迭代计算以减少计算时间和过程,提高数值模拟效率。根据本文研究要求选择采用WHS解算器进行模型模拟计算,需要对其中的一些相关参数进行初步设置。
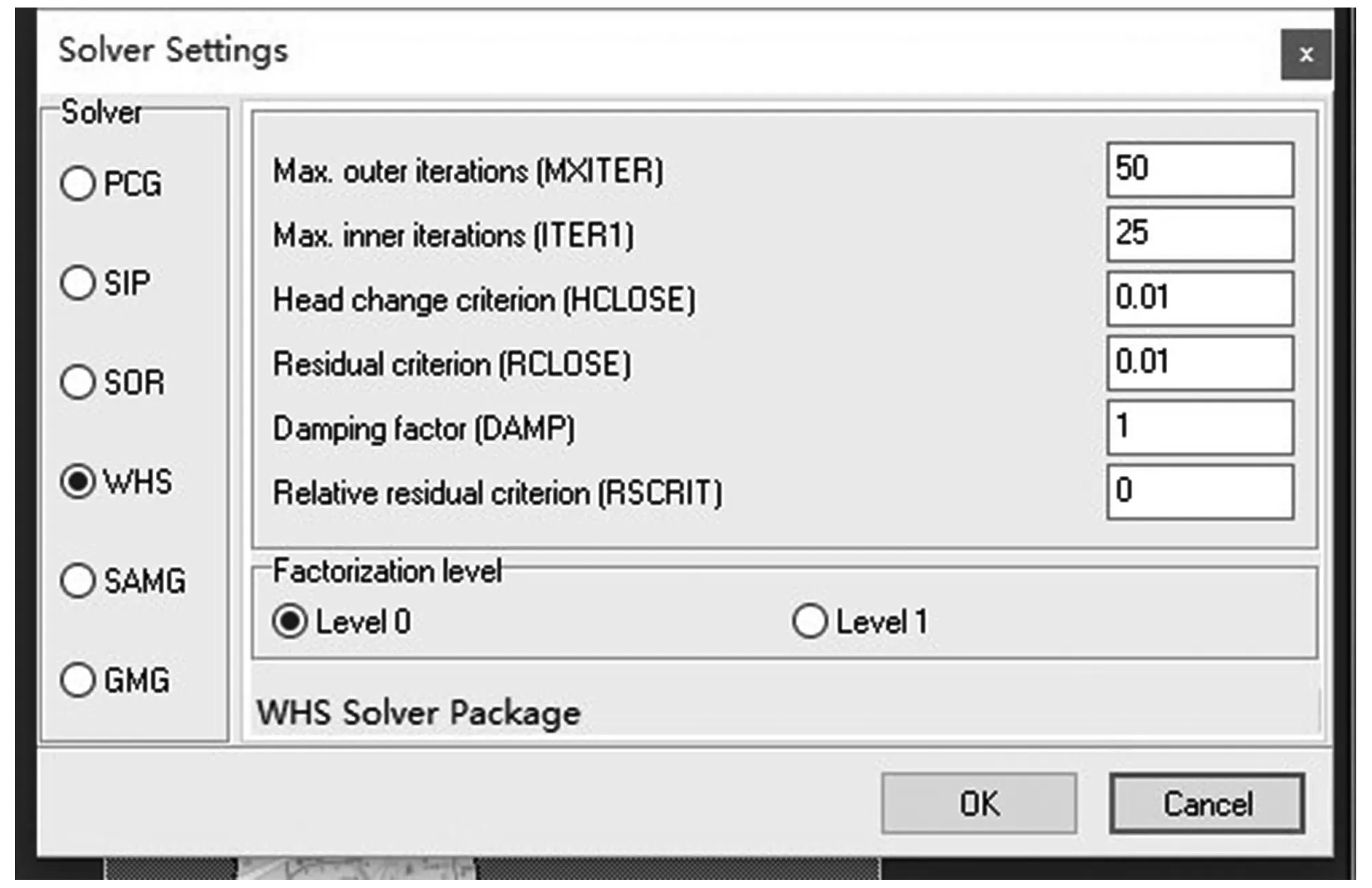
图4 WHS法主要参数设置图Fig.4 Main parameter setting in WHS method
2.3 数值模型的建立
(1)模型剖分。依据位山灌区试验站提供的灌区区域图和DEM图,采用ArcGIS软件进行图形校准并进行矢量化处理和灌区高程提取,其分别作为构建数值模型的底图和模型地表高程数据。根据灌区面积和数据质量以及模拟结果精度要求,使用Visual Modflow软件对灌区模型进行网格划分,如图5。灌区模型共被划分为200×200(行×列),其中有效单元格(白色部分)为24 057个,无效单元格(绿色部分)为15 943个;蓝色区域为灌区的河流补给边界;由于研究对象为浅层含水层,因此在垂直方向上设定一层,而灌区含水层的底板标高设置为60 m。图5中显示为白色的区域均为有效研究单元格,而绿色区域的单元格为无效,模型计算时不进行模拟计算,计算节点位于剖分单元中心。
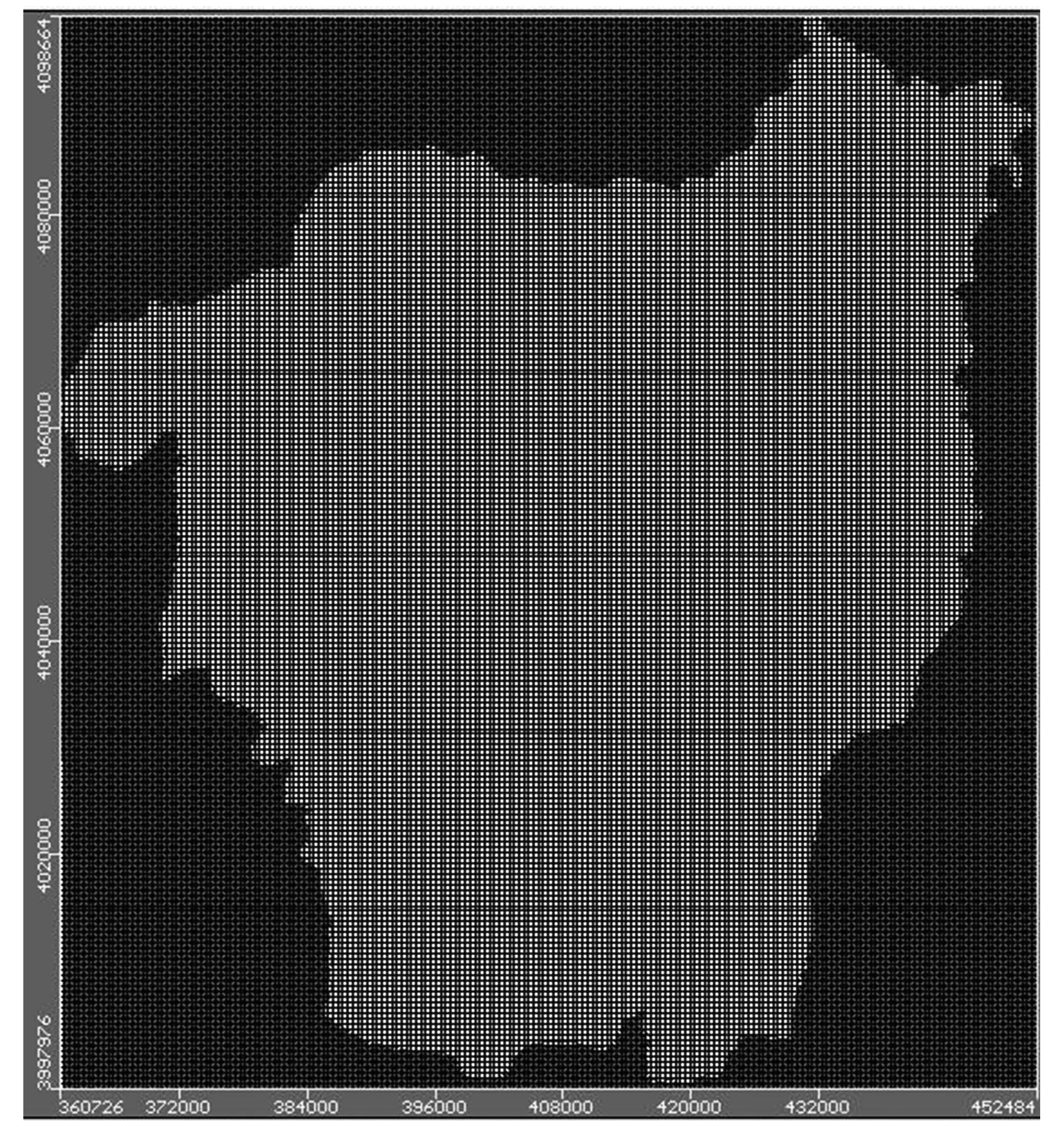
图5 研究区域网格剖分图Fig.5 Mesh generation of study area
(2)模型初始参数设置。根据位山灌区试验站提供的灌区水文地质勘察报告和抽水试验资料,结合前人所得经验参数值作为模型相关参数初始值,详见表3。
(3)边界条件的处理。模型边界主要由研究区域的四周边界和河流边界组成。根据上述边界条件,依据灌区地下水流场分布特征确定该边界参数,采用Visual Modflow软件中的GHB程序包对该边界赋值通过调节边界水头控制边界对模型的补给和排泄。
基于聊城市提供的相关等资料,结合相关文献,确定不同河流在各河段的渗透系数,利用软件自带的river程序设定相关参数赋值计算。模型底层设定为不透水边界。详见图6。
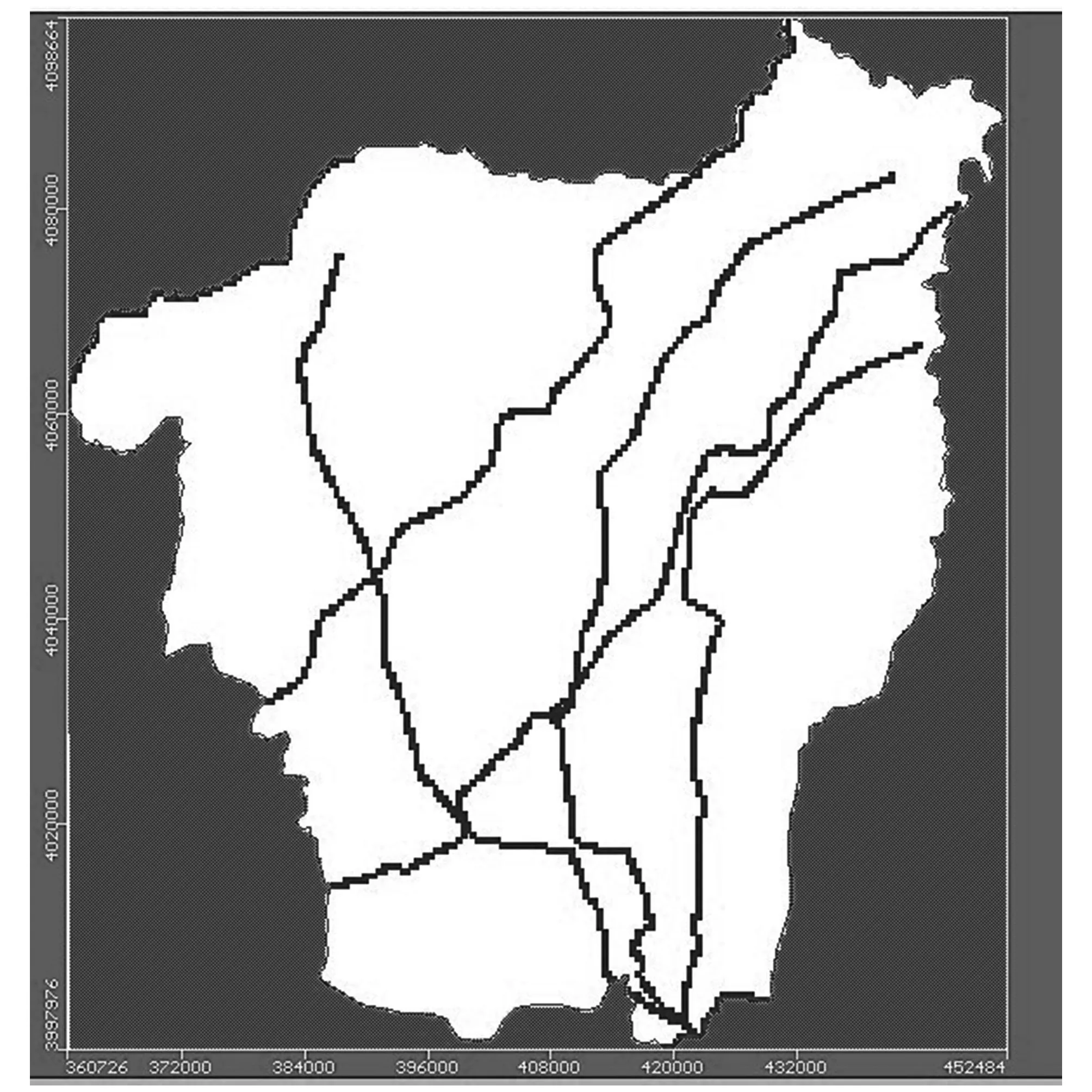
图6 灌区模型边界条件设置图Fig.6 Boundary condition set of irrigation area model
(4)模拟期的确定。依据位山灌区试验站提供的地下水位监测资料以及聊城市水文局提供的灌区降水、蒸发等水文资料,分别选择2010.1.1-2011.12.31期间的地下水数据和水文资料作为地下水数值模型调参校准和验证的基础数据。其中选择2010.1.1-2010.12.31期间的相关数据作为模型构建数据,主要用于模型参数的识别和调整;而2011.1.1-2011.12.31期间的数据主要用于数值模型的可靠性验证分析。根据研究数据完整程度,模型识别和验证时段均为被划分为12个时段,每个时段内模型的降水灌溉等补给项和蒸发等排泄项是一致的。
3 结果与分析
3.1 灌区模型的识别
模型识别是指通过不断地调整模型中的相关参数,每调整一次使用模型运行模拟地下水位,然后分析其与该时段实测水位的误差,如果误差较大则需要再一次调整,直至模拟水位和实测水位误差满足要求为止,即模拟曲线和实测水位能够最佳拟合。
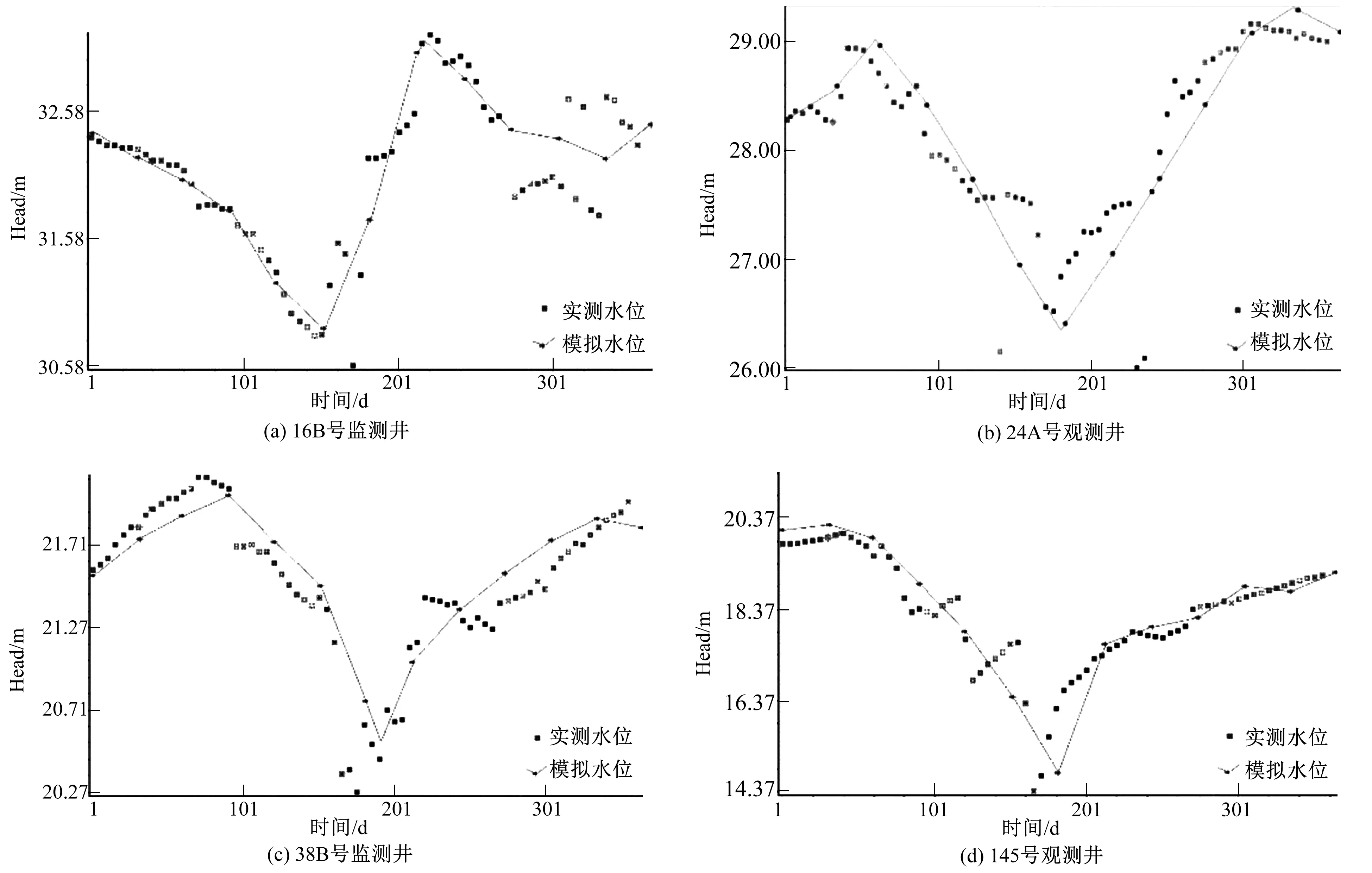
图7 研究区监测井实测水位与模拟地下水位拟合曲线Fig.7 Fitting curve of measured and simulated water level of monitoring well in study area
位山灌区内共布设了25眼地下水位监测井,而且具有长期的地下水位实测数据。选择2010年实测地下水实测资料作为数值模型识别数据,同时选择2010年6月7日灌区地下水流场和模拟流场进行对比分析。经过不断调整校准模型中的渗透系数等参数,使地下水位模拟结果与实测水位拟合程度较高。
在模型识别期内,在研究区域内选择4个典型地点和两个对比流场进行模拟拟合分析。由图7可知,四个典型地点的地下水位模拟结果和地下水位实测结果拟合程度较好,二者动态变化趋势基本一致。选择2010年6月7日的模拟地下水流场分布图和实际流场分布图基本相符,详见图8。按照《地下水资源管理模型工作要求》(GB/T14497-93)对比分析灌区所有监测井的模拟结果和实测数据可知,拟合误差小于1 m的监测井有21个,占有所有观测孔的84%,同时计算各观测井水位实测值和模拟值的残差均值为0.37 m,二者的相关系数为0.965。
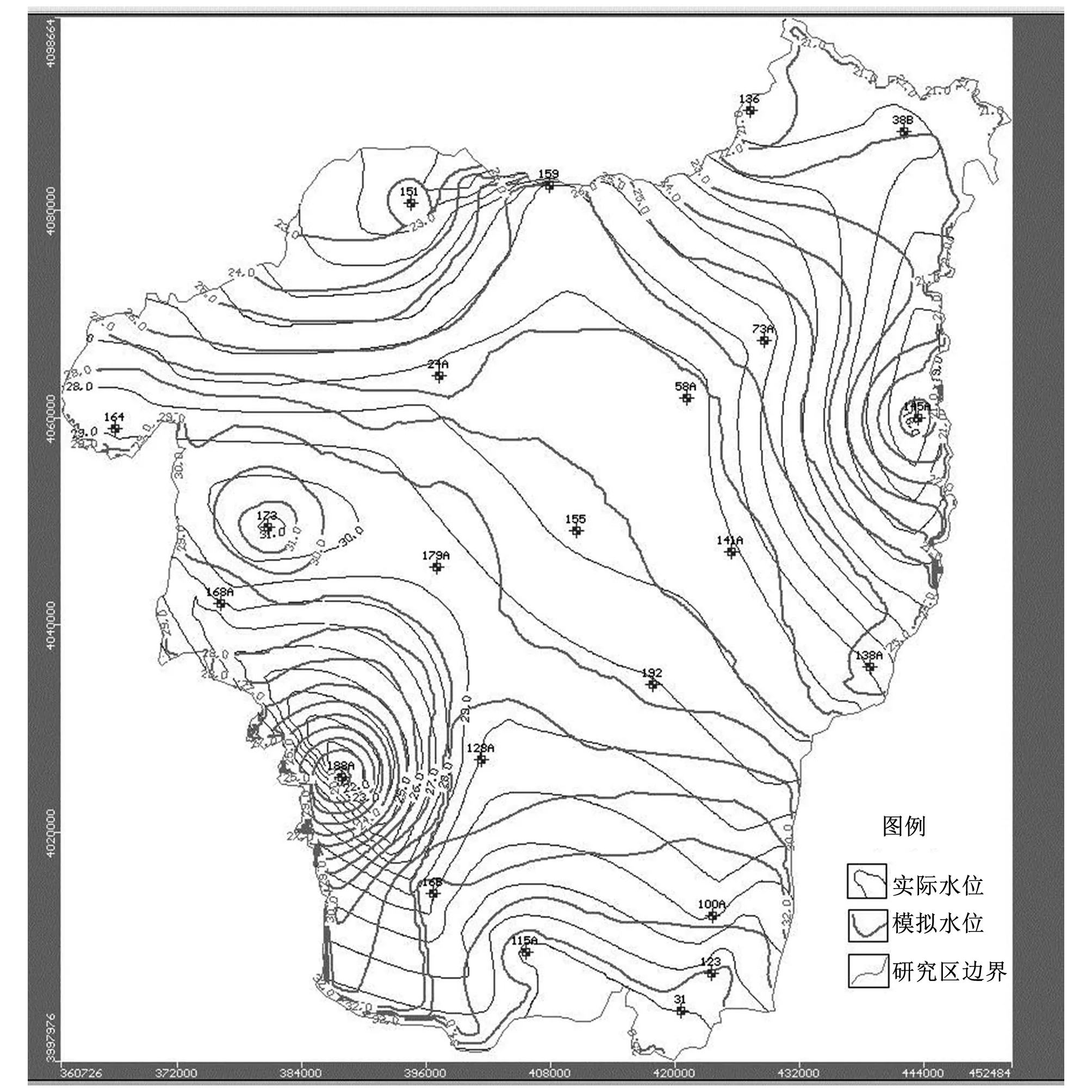
图8 2010年6月7日模拟流场与实际流场对照图Fig.8 Comparison of simulated flow field and actual flow field on 7, June,2010
综上所述,地下水位模拟值和实测值存有一定误差,但是均分布在95%的置信区间内,模拟结果未出现误差累计和误差扩大问题,表明该模型的相关参数设置合理(详见表4),可以真实反映研究区域水文地质概念模型的水文地质参数,识别后的数值模型可以用于研究灌区地下水位的动态变化和水量转化关系。

表4 模型相关参数值Tab.4 The Correlation parameter values of model
3.2 灌区模型的验证
模型识别确定后需要根据研究区域识别期以外的数据进行模型验证以确定模型是否真的可以准确反映研究区域地下水动态变化。基于已识别模型,以模型运行结果作为初始条件,其他参数、边界等条件不变,模拟时间为1年,运行模型。最后选择2011年灌区水位实测数据和模拟结果对比分析以确定数值模型的准确性和可靠性。
根据模型模拟结果选择4个典型观测井(异于识别时选择的观测井)的实测水位进行对比分析,详见图9。通过分析四个观测井实测水位和模拟水位拟合曲线可知,模拟水位和实测水位拟合度较高,一些时间段模拟水位与实际水位存在偏差,但是水位动态变化趋势基本一致。

图9 研究区监测井实测水位与模拟地下水位拟合曲线Fig.9 Fitting curve of measured and simulated water level of monitoring well in study area
通过建立模型对2011年1月-2011年12月的位山灌区进行水均衡模拟,结果详见表5。依据《位山灌区地下水资源评价报告》可知在采用水量均衡法计算得出浅层地下水补给量是103 512 万m3,浅层地下水过度开采量是3 225.4 万m3,与模型模拟结果分别相差4.2和10.2 万m3,可见水均衡模拟结果符合灌区实际情况,地下水数值模型模拟结果可靠。
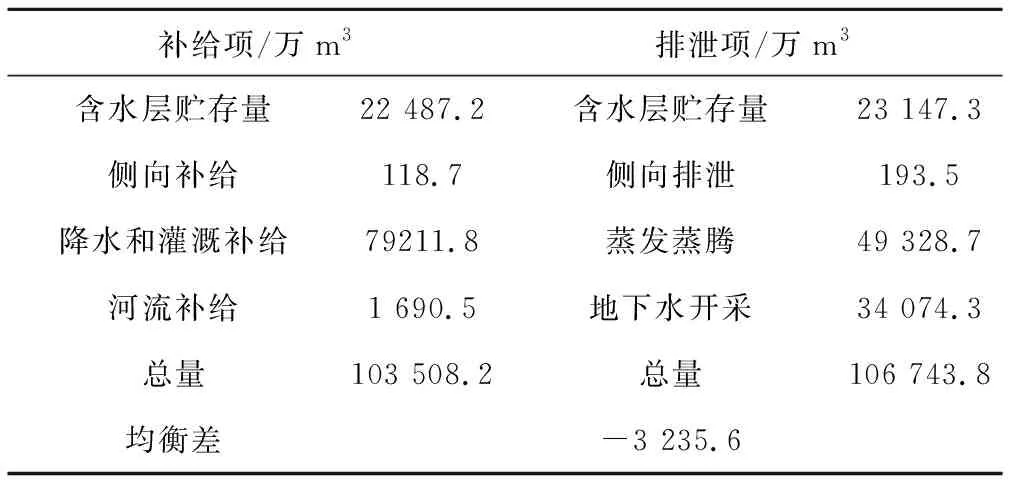
表5 研究区域浅层地下水水量均衡分析表Tab.5 Water equilibrium analysis of shallow groundwater in irrigation area
3.3 地下水量均衡与水位波动分析
(1)地下水量均衡分析。区域地下水量均衡是指在一定时段内研究区域内地下水补给量和排泄量之间的相对关系,即补给量大于排泄量称之为正均衡反之为负均衡。本文依据翔实的地下水位监测资料以及识别验证后的数值模型,对研究区域进行地下水量均衡计算,详见表6。
由表6可知,在不同保证率下,降雨量不同,补给总量随着降雨量的减少而减少;补给项主要包括降水入渗补给量、农业灌溉水下渗补给量等,补给项受降雨影响较大,而排泄项主要是蒸散发量、地下水开采量等,受降雨影响较小,所以表6中,随着降雨量的较少,补给总量减少明显,排泄项量变化不大,均衡差增大。
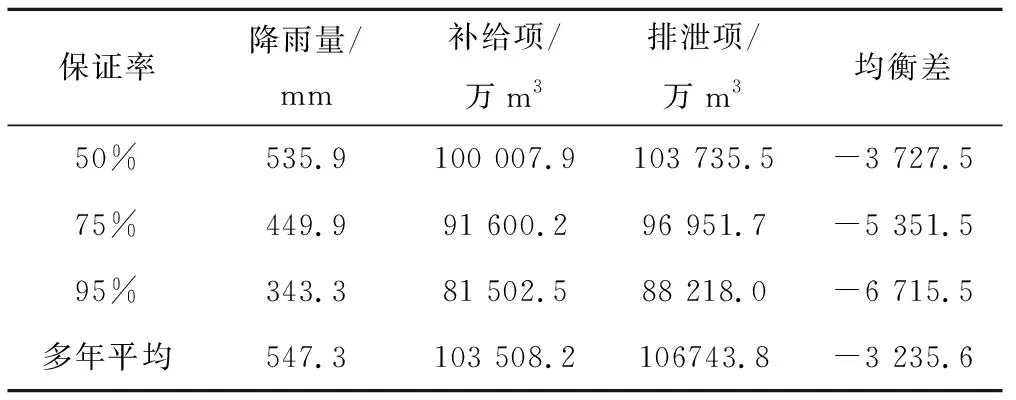
表6 不同保证率下浅层地下水量均衡分析表Tab.6 Water equilibrium analysis of shallow groundwater under different guaranteed rates
(2)地下水位波动分析。大气降水是浅层地下水的主要补给来源,降水与地下水位回升具有明显的相关性。文中取16B号监测井进行试验,观测地下水位在不同保证率下的变化,见图10。

图10 不同保证率下监测井水位分析图Fig.10 Analysis of underground water level of monitoring well under different guaranteed rates
由图10可知,在不同保证率下,水位变化趋势大致相同。但是,随着降雨量的减少,地下水位降低,水位埋深越来越低,可见降雨量与地下水位呈正相关。
4 结 论
(1)MODFLOW模型程序结构合理,离散方法简单,求解方法多样化,易于操作,是一种适合于模拟地下水流动态的数值模拟软件,且拟合度较高,较为准确,具有广泛的应用价值。
(2)由模拟结果可知灌区在模拟期内地下水补给总量是103 508.2 万m3,排泄总量是106 743.8 万m3,二者相差-3 235.6 万m3,由此可知位山灌区目前地下水系统属于负平衡状态。
(3)位山灌区浅层地下水过度开采量为3 225.4 万m3,与模型模拟结果分别相差10.2 万m3,表明灌区地下水均衡模拟结果可靠,符合灌区实际情况。
(4)大气降水是影响水量均衡、地下水位波动的重要因素,且大气降水与水量均衡、地下水位呈正相关。
□
