基于天气预报和符号回归算法的参考作物腾发量预测研究

2018-08-29刘博弈王海渝刘文豪徐俊增

中国农村水利水电 2018年8期

刘博弈，王海渝，龚严,2，刘文豪，卫琦,3，徐俊增,3

(1.河海大学农业科学与工程学院，南京 210098; 2.河海大学水利水电学院，南京 210098; 3.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098)

0 引言

中国农业用水占总用水比例大，发展节水灌溉对农业的可持续发展至关重要[1]。节水灌溉的关键是进行实时的灌溉预报，而逐日作物腾发量的预测是实时灌溉预报的基础[2]。参考作物腾发量(Reference crop evapotranspiration，ET0)是计算作物腾发量的重要参数之一，ET0的准确预报对于灌溉计划以及区域水资源分配具有重要的指导意义。

鉴于上述研究不足，本文以天气预报和符号回归算法为基础，拟提出一种新的ET0预测模型，并在干旱区和湿润区分别选择典型站点对其预测精度进行评价，其研究结果对于不同气候区实现ET0准确预测以及制定有效合理的灌溉计划具有重要意义。

1 材料与方法

1.1 数据来源

本文选取位于湿润区和干旱区的6个典型站点(各3个)作为研究对象，从中国气象数据网(http:∥data.cma.gov.cn)分别收集了6个站点1989-2016年逐日历史实测气象资料，包括历史逐日的最高气温、最低气温、平均气温、日照时数、平均风速以及平均相对湿度。并在天气网(http:∥www.tianqi.com)收集了6个站点在2013-2016年逐日历史天气预报，包括日最高气温、日最低气温、天气类型和风力等级。6个站点的基本信息如表1所示。

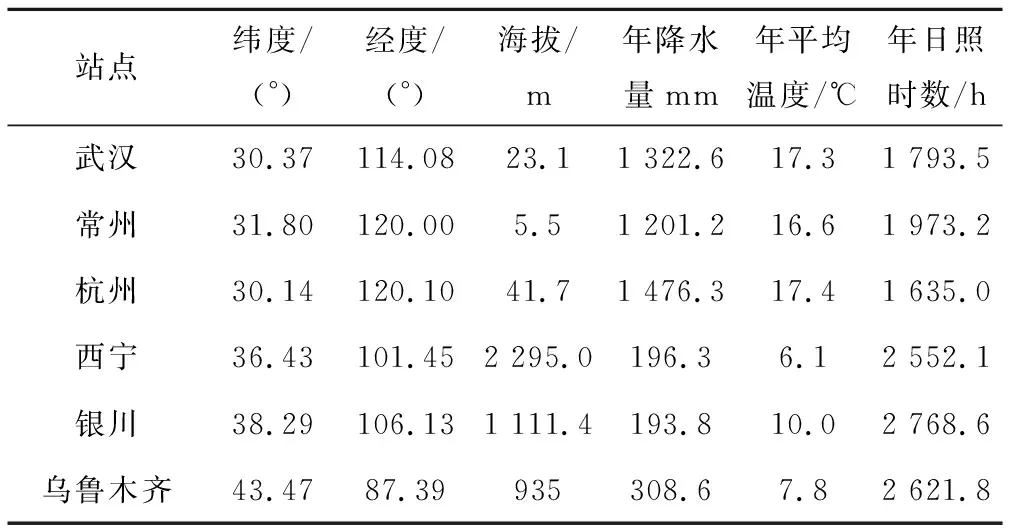
表1 典型站点基本信息Tab.1 Basical information of typical stations

1.2 ET0预报模型

1.2.1 HS方法及其地区率定

HS公式是一种基于温度估算ET0的方法，由于其需要的气象数据少，常用于ET0预报。其表达式[13]为：

ET0,HS=0.408×a×(Tmean+17.8)×TRc×Ra

(1)

式中：ET0,HS为采用HS公式计算得到的参考作物腾发量，mm/d；TR和Tmean分别为逐日温差以及平均温度，℃，可由日最高气温Tmax和最低气温Tmin计算得到，Tmean=(Tmax+Tmin)/2，TR=Tmax-Tmin；Ra为天顶辐射，MJ/(m2·d)；参数a和参数c需要根据当地气象资料率定。

由于FAO56 PM公式[14]计算精度高，被广泛用于评价其他ET0预报和估算模型。本研究以1989～2009年历史实测气象资料为率定样本，以PM公式计算的ET0为对照，对HS公式的参数a和参数c进行率定，并以2010-2016年气象数据为验证样本。将2013-2016年气象预报数据输入，对率定后的HS公式进行ET0预报精度分析。

1.2.2 符号回归算法

图1所示为单相PWM整流的拓扑图,Un和In分别为电路交流侧的电压和电流,Rn为线路电感,Ln为交流侧电流,Udc为直流侧电压,C2为直流侧储能电容,单相PWM整流电路主要通过将交流能量通过IGBT的开关状态转换成直流能量,通过调整不同开关状态的持续时间,可以控制直流侧电压的大小,同时保证交流侧的输入电压和输入电流为同相位,保证单位功率因数的能量传输。

符号回归算法(SR)是在Eureqa软件应用上逐步发展完善[15, 16]。运用符号回归算法建立模型，需要确定输入的自变量以及因变量，函数组成以及适应度函数[12]。本文选用的函数组成包括C(常数)、x(输入变量)、ex、lg(x)、sqrt、幂、+、-、×、÷，选择拟合优度R2作为衡量标准。拟合优度越大，模型估算精度越高。程序自动运行后将对产生的模型进行反复修正评估，直到产生的模型稳定且满足衡量标准，即运行结束。本文从产生的模型中挑选出拟合优度R2最大的模型作为SR模型。

以最高气温Tmax，最低气温Tmin，相对日照时数(Relative sunshine duration，n/N)，天顶辐射Ra为自变量，以1989-2009年历史实测气象资料为率定样本，以PM公式计算的ET0为对照，经2010-2016年验证期验证后建立ET0符号回归估算模型。其模型如下：

ET0,SR=f(Tmax,Tmin,n/N,Ra)

(2)

n/N是估算净辐射的重要参数，一些学者将天气预报中天气类型解析为相对日照时数用于ET0预测[7, 17]，但天气类型预报精度需要提高。也有相关研究利用温度建立相对日照时数定量表示模型[18]。本文以最高气温Tmax，温差TR为自变量，以1989-2009年逐月历史实测资料为率定样本，以实测资料计算的n/N为对照，经2010-2016验证期验证后建立逐月n/N符号回归估算模型，模型表达式如下：

n/N=f(Tmax,TR)

(3)

式中：Tmax和TR分别为日最高气温和温差，℃；n/N为逐日相对日照时数，由日照时数n和白昼最大可能时长N来确定。具体公式见文献[14]。

将2013-2016年天气预报数据先代入到模型(3)得到n/N预报值，再将同时期温度预报数据与n/N预报值代入到模型(2)进行ET0预报。

1.3 误差分析

采用均方根误差(RMSE)、平均绝对误差(MAE)和加权决定系数(WR2)等3个统计指标来评价ET0预报精度，并采用准确率分别评价气温预报和ET0预报，具体公式参见文献[8, 12]。

2 结果与讨论

2.1 气温预报精度评价

典型站点的最低和最高气温预报准确率如图1所示。可以看出，位于干旱区的典型站点的最高、最低气温预报的平均准确率(72.39%和79.41%)均略低于位于湿润区的典型站点的值(82.48%和84.98%)，且这一差异在最高气温的预报精度上表现更为明显。可见，气温预报在湿润区各站点的精度比在干旱区各站点更为稳定，这可能与采用不同的气温预报模型相关[19]。整体上，不同气候区的典型站点最低气温预报的准确率均略高于最高气温预报准确率，与李国翠等[20]的研究结果较为一致。

图1 各站点气温预报准确率的比较Fig.1 Comparison of accuracy of the forecasted temperature in different stations

2.2 HS公式率定与验证

表2给出了HS公式参数率定结果，可以看出，位于相同气候区的站点参数取值大致落在相同范围，且参数值范围与胡庆芳等[21]研究结果较为一致，差别可能是由于所采用时间步长不同导致。

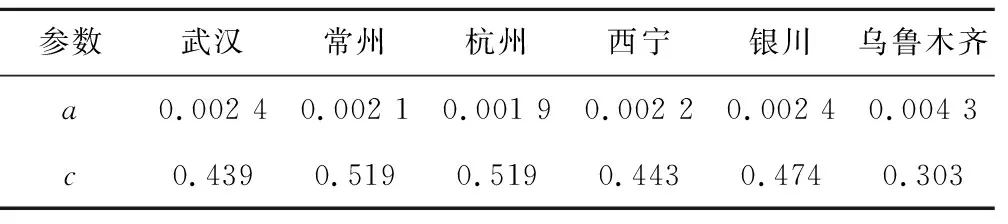
表2 HS公式参数修正结果Tab.2 Results of parameter correction of the HS model

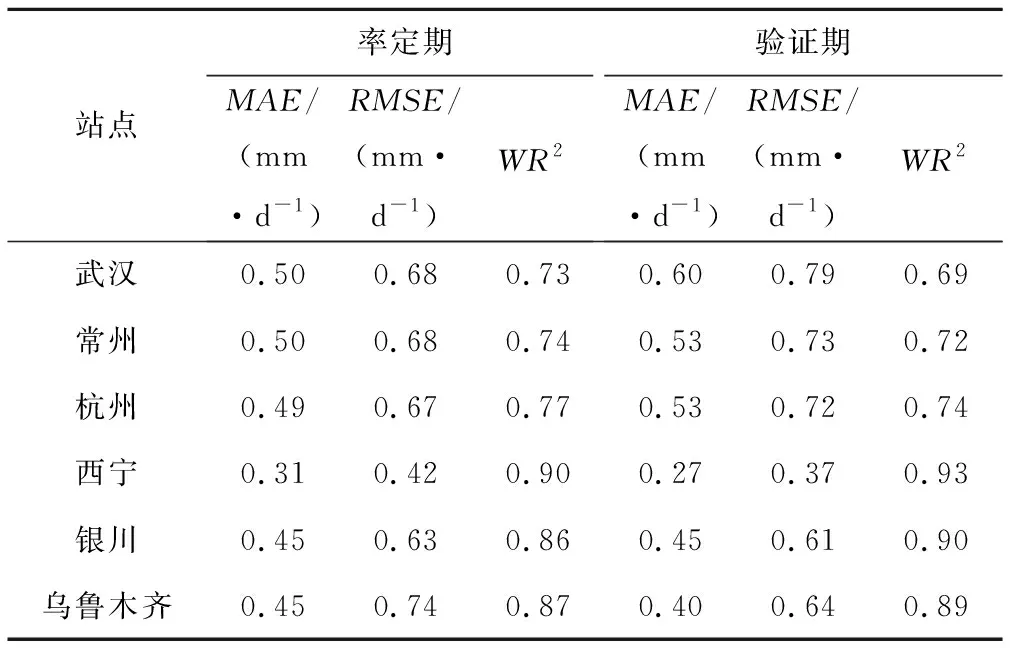
表3 HS公式率定期和验证期统计指标Tab.3 Statistical indices for HS models in calibration period and validation period

以PM公式计算结果为对照，进一步分析率定后的HS公式在各站点率定期和验证期的误差情况(表3)，可以看出，率定后的HS公式在各站点的率定期和验证期其MAE和RMSE均维持在较低水平，且HS公式在位于干旱区的站点精度略高于位于湿润区的站点，但在总体上率定后的HS公式在各站点均保持较高的精度，可以应用到预报中。

2.3 ET0符号回归估算模型

以PM公式和1989～2009年历史气象资料计算的ET0作为基准，通过符号回归算法建立ET0与各气象因素之间的定量关系，以决定系数(R2)最大作为筛选依据，筛选出各站点的ET0符号回归估算模型，分别如下式(4)～(9)所示：

0.026Tmax(n/R)Ra-0.65

(4)

ET0,SR常州=0.171 3+0.045 69Ra+0.022 98Tmin+

(5)

0.002 994Tmax(n/R)Ra-0.310 5

(6)

ET0,SR西宁=0.11(n/N)Ra+0.002 4TmaxRa-

0.020 8 8Tmax-2.2 (n/R)+0.82

(7)

ET0,SR银川=0.032 68Ra+0.002 093TmaxRa+

(8)

ET0,SR乌鲁木齐=0.05Ra+9×10-4TmaxRa+

(9)

以2010-2016年实测气象数据为验证样本，以PM公式计算结果为对照，对ET0符号回归估算模型的估算精度(图2)进行分析，可以看出，与率定后的HS公式相比，SR模型在各站点的ET0计算精度显著提升，回归直线方程斜率均接近1，加权决定系数WR2均超过了0.91，干旱区和湿润区各站点采用SR模型的MAE值较率定后的HS公式分别平均降低了49.56%和28.40%，RMSE分别减少了48.90%和29%。可见，SR模型在引入相对日照时数输入变量后，ET0估算精度得到明显提高。

2.4 基于天气预报数据的ET0预测结果评价

以2013-2016年历史逐日天气预报数据为依据，以PM公式计算值(ET0,PM)为对照，分别对率定后的HS公式和SR模型的ET0预报值(ET0,HS和ET0,SR)进行评价(如图3所示)，可以看出，整体上，两种方法在各站点的预报值均与PM公式计算值变化趋势较为一致，与PM公式相比，引入相对日照时数的SR模型和率定后的HS模型对ET0的预报精度均有明显提升，SR模型的ET0预报精度略高于率定后的HS模型，且其提升幅度在湿润区各站点表现得更为明显。

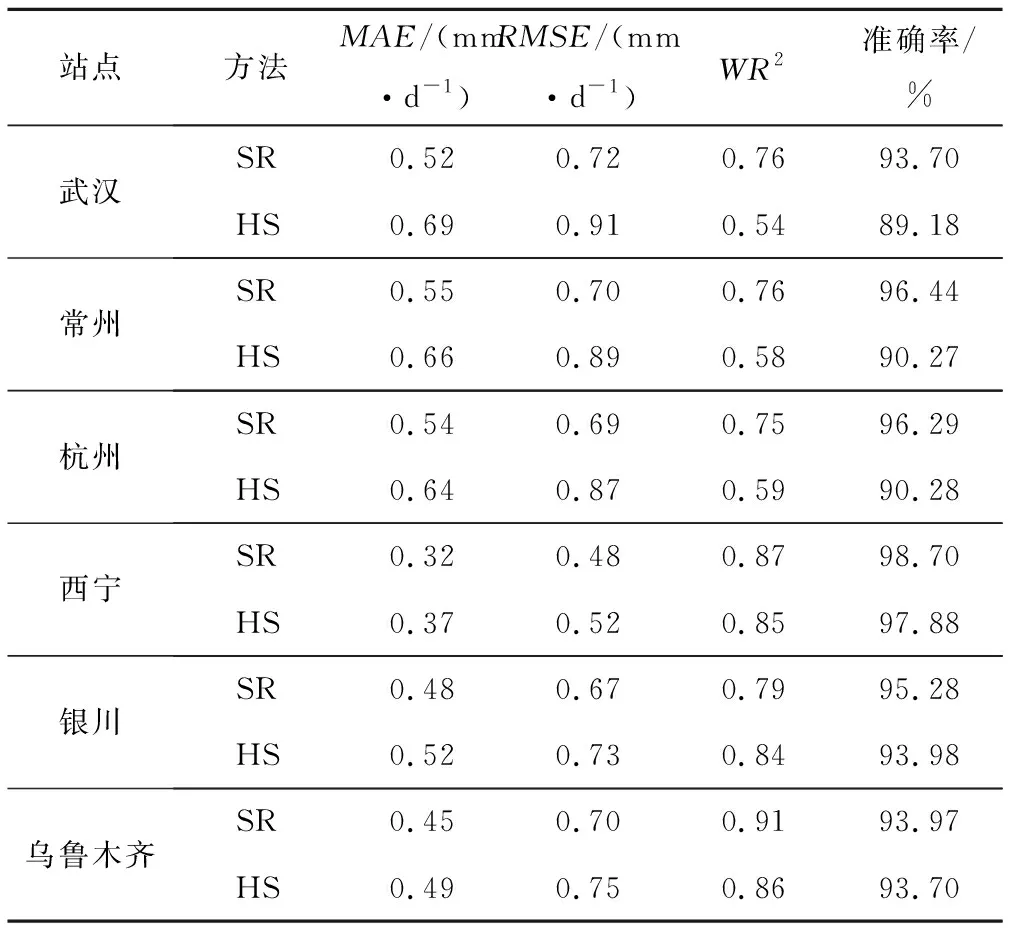
进一步分析SR模型和HS模型的ET0预报精度(表4)，可以发现，与率定后的HS公式的计算结果相比，位于湿润区的各站点采用SR模型的MAE、RMSE值分别平均减少了18.98%和20.97%，WR2和准确率分别平均增加了24.65%和5.57%。而位于干旱区的各站点SR预报模型MAE、RMSE值分别减少了9.79%和7.53%，WR2和准确率分别平均增加了0.49%和0.80%。

HS公式虽然预报精度整体较高，但仍存在一些缺陷。由于不考虑风速以及相对湿度的影响，在极端风速情况下，预报精度较低[9]。例如位于干旱区的乌鲁木齐2015年7月22日ET0达到了11.6 mm/d，最高温与最低温度预报值只相差1.4 ℃和0.8 ℃，而实测风速为5.9 m/s，使得HS预报值仅为7.7 mm/d。此外在位于不同气候区的站点预报精度差异较大，位于湿润区各站点HS预报的MAE值平均比干旱区增大了30.3%，HS公式在位于湿润区的各站点预报效果较差，这也与Xu等[2]研究结论一致。

图2 验证期符号回归模型ET0估算值与PM公式ET0计算值的关系Fig.2 Relation in ET0 between those caculated by SR and PM models during validation period

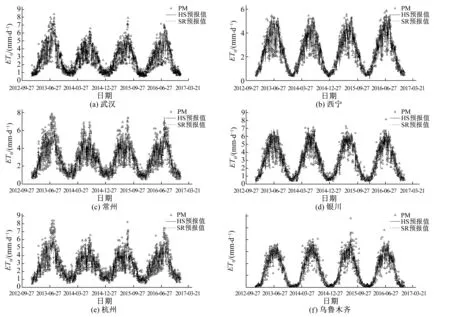
图3 2013-2016年ET0预报值和PM计算值过程变化图Fig.3 Variation patterns for forecasted ET0 and ET0 calculated from PM model (2013-2016)

站点方法MAE/(mm·d-1)RMSE/(mm·d-1)WR2准确率/%武汉SR0.520.720.7693.70HS0.690.910.5489.18常州SR0.550.700.7696.44HS0.660.890.5890.27杭州SR0.540.690.7596.29HS0.640.870.5990.28西宁SR0.320.480.8798.70HS0.370.520.8597.88银川SR0.480.670.7995.28HS0.520.730.8493.98乌鲁木齐SR0.450.700.9193.97HS0.490.750.8693.70

符号回归算法通过引入相对日照时数，使得ET0预报精度较HS公式提高，但在不同气候区提升幅度不同。湿润区夏季雨量增多导致湿度增大，使得HS公式在夏季计算误差较大，且湿润区夏季天气类型变化较大[9]，引入相对日照时候后即增加了天气类型的修正，因而使得在湿润区提升幅度较高。例如武汉站点HS模型在夏季AAE值为2.04 mm/d，而SR模型AAE值仅为1.32 mm/d。而干旱区风速ET0对风速较为敏感，SR模型没有考虑风速的影响，且HS公式在干旱区预报精度较高，因此在干旱区SR模型提升幅度较小。