华北平原地区农田产流模型构建及检验

王现领，刘嘉男

(1.天津市水利科学研究院，天津 300061；2.山东省水利勘测设计院，山东 济南 250013)

通过现场勘察，遴选出封闭的农田排水小区并进行了水文数据量测，采集近两年的降水及对应降水时段的排水量、土壤含水量、地下水位等实测数据，实测数据以1 h为计算时段进行整理，排水小区水文数据汇总见表1。

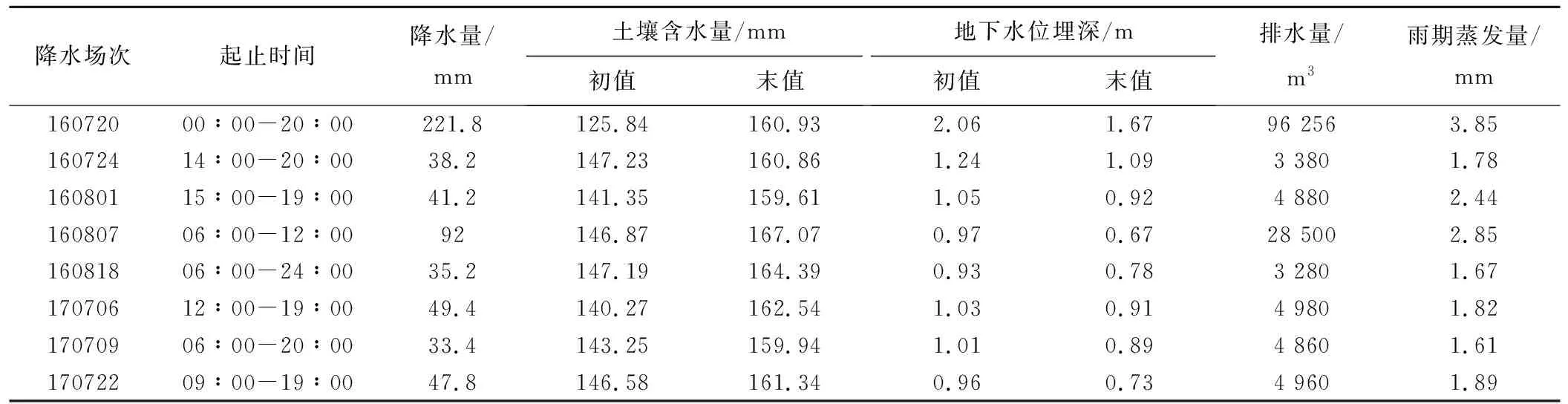
表1 排水小区水文数据汇总表Tab.1 Summary of hydrological data in drainage area

结合北方平原区农田产流特性，充分考虑在北方平原区可能同时发生超渗和蓄满产流现象，建立超渗-蓄满垂向耦合产流模型，采用有更好鲁棒性的Sobol'法进行敏感性分析，通过模型参数的一阶敏感度和总敏感度分析，确定产流模型的敏感性参数。模型参数率定采用参数优选中最有效的SCE-UA算法，通过参数自动率定与人工率定结合法，得到优选参数。选取径流深相对误差、地下水位相对变化量与土壤含水量变化量的相对误差和Nash效率系数为指标，评价模型的适用性。并通过与超渗产流模型、蓄满产流模型进行对比检验，进一步验证超渗-蓄满垂向耦合产流模型的合理性。

1 产流模型研究现状

目前，国内外有关产流的研究已涌现出很多水文模型，主要分为集总式水文模型和分布式水文模型，集总式水文模型是以流域整体为研究对象，而分布式水文模型则是将流域划分为很多较小单元，并假定各单元内部属性的相对一致性，从而进行产汇流模拟。我国水文研究者分析改进降水-径流相关图，创建了以新安江模型为典型的蓄满产流模式和以Horton模型为代表的超渗产流模式[1]，该产流理论对于流域的面积大小无特殊要求，所需数据较易获得，可用于小尺度平原地区产流计算。但对于多数流域，并不单单只有一种产流模式，通常两种产流方式交叉存在，混合式产流模型因其模型机制更加完善，更符合区域产流实况而逐渐得到推广，并成为今后产流模型研究的重点。

2 产流计算

采用超渗-蓄满垂向耦合产流模型，即空间分布的下渗曲线与蓄水容量分布曲线的耦合，首先判断是否发生超渗产流，当发生超渗产流时，采用具有流域分布特征的格林-安普特下渗曲线计算超渗产流量和下渗量[2]，超渗产流的下渗量即为蓄满产流中的降水输入量。在土壤缺水量大的面积上，下渗的雨量首先补充土壤含水量不产流，而在缺水量小的面积上，补足土壤缺水量后，发生蓄满产流。

超渗产流量计算过程为：

PE=P-E-I

(1)

(2)

FMM=FM×(1+B1)

(3)

(4)

R1=PE-FA

(5)

式中：P为降水量，mm；E为蒸发量，mm；I为植物截留量，mm；PE为净雨量，mm；FM为农田小区平均下渗能力，mm/h；FC1为稳定下渗率，mm/h；K2为土壤缺水量对下渗率影响的灵敏度系数；FMM为平均下渗率为FM时上层最大点的下渗率，mm/h；FA为实际下渗量，mm；WM为土壤平均蓄水容量，mm；W为土壤含水量，mm；B1为下渗能力分配曲线的指数，反映了下渗能力分布的不均匀性；R1为超渗产流量，mm。

地面以下的径流，采用蓄满产流，计算公式为：

(6)

WMM=WM×(1+B2)

(7)

(8)

式中：A1为前期影响雨量，mm；WMM为土壤内最大点蓄水容量，mm；B2为蓄水容量～面积分配曲线的指数，反映了蓄水容量分布的不均匀性；R2为蓄满产流量，mm；式中其他符号含义同前。

总产流量R为超渗产流量R1与蓄满产流量R2之和，即：

R=R1+R2

(9)

蓄满产流计算出的产流量R2包括地面径流R2S和地下径流R2G两部分，可以用稳定下渗率进一步划分。计算过程如下：

(10)

式中：FC2为下层土壤稳定下渗能力，mm/h。

蒸发量与土壤含水量的计算采用三层蒸发模式，将植物的截留作用合并于降水的蒸发损失中，构成了完整的超渗-蓄满垂向耦合产流模型。

3 模型参数敏感性分析

3.1 分析方法

敏感性分析方法采用Sobol'法，与传统的敏感性分析方法相比具有更好的鲁棒性，能更好地解决非线性问题[3]。模型表示为：

y=f(X)=f(X1,…,Xm) 0≤X1≤1,i=1,2,…,m

(11)

式中：y为模型输出的目标函数；X=X(Xi,…,Xp)为模型的参数。那么y的方差D(y)可以作如下分解：

(12)

式中：Di为参数i产生的方差；Dij为两个参数i和j相互作用产生的方差；Dijk为3个参数i、j、k相互作用产生的方差；D1,2,…,m为m个参数共同作用产生的方差。将上式归一化后得到各参数和参数相互作用的敏感性：

(13)

产流模型参数i对目标函数的敏感度值可表示为：

一阶敏感度：

(14)

二阶敏感度：

(15)

总敏感度：

(16)

式中：Si为参数i作用的敏感度；二阶敏感度Sij为两个参数i和j相互作用的敏感度；总敏感度STi为参数i主要作用和相互作用的敏感度；D～j为除了参数 之外的参数的方差。

计算参数的各阶敏感度实际上是计算参数的各阶方差，由于水文模型具有很大的非线性和复杂性，方差的计算参照前人的建议[4]选用拉丁超立方体抽样对产流模型中待分析的变量进行两次独立抽样，得到ON×m和PN×m两个矩阵，其中 为抽样次数，m为参数个数，通过下列公式进行计算，即：

(17)

(18)

(19)

(20)

(21)

(22)

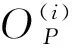
结合式(11)、式(12)、式(13)就可以得到产流模型参数各阶敏感度系数值。

因为没有关于参数的先验信息，进行敏感性分析输入的参数值是从均匀分布中抽取的，不同的参数范围在0～1之间进行线性变换[5]。产流模型中参数的取值上下限见表2。利用拉丁超立方体抽样，在参数的取值范围内随机生成包含2 000组参数的两个样本。

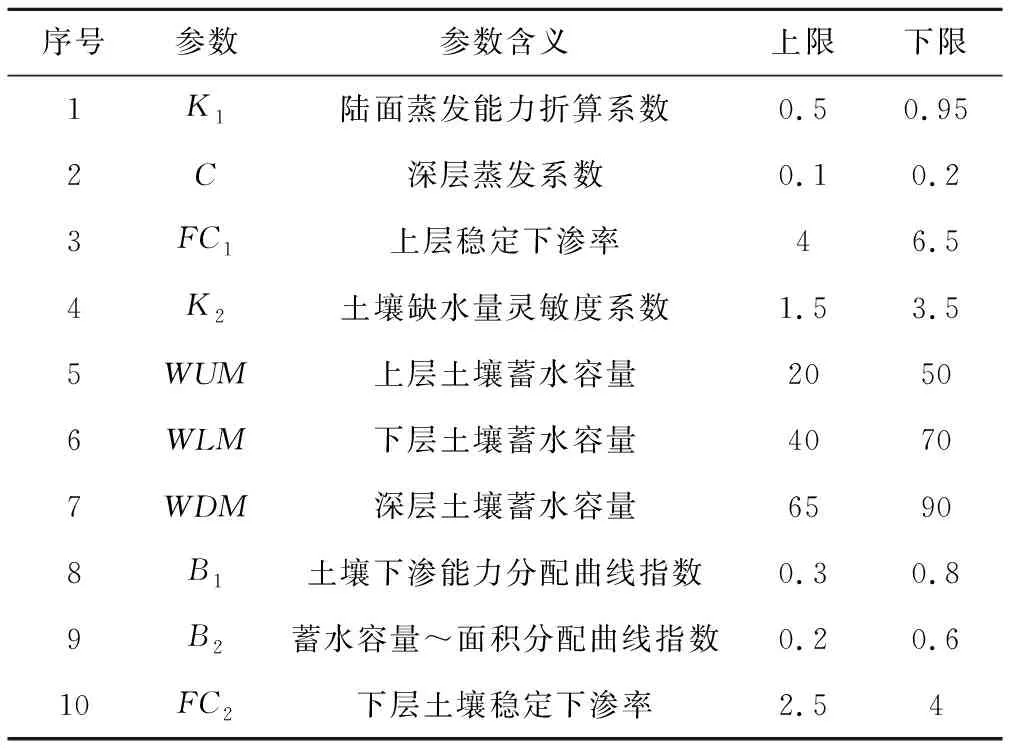
表2 模型参数意义及取值范围Tab.2 Model parameter meaning and range of value

3.2 分析结果

根据赵人俊[6]的研究，结合垂向耦合模型结构，待分析参数可以划分为4个层次，见表3。

表3 模型参数分层Tab.3 Model parameter stratification

其中，在该模型中IMP、α、β均为定值，IMP为不透水面积比例，该农田小区为0.41，不透水面上的产流系数α取0.95，透水面积流入沟渠的径流分配系数β取0.3。

五场降水中，通过对模型中十个参数对径流深目标函数的一阶敏感度及总敏感度进行分析，确定该产流模型的敏感性参数为：WUM、WLM、WM(WDM)、FC1、K2、FC2，在进行模型参数率定过程中，综合考虑这些参数对模型结果的影响。

4 模型参数率定

4.1 自动率定方法

自动率定方法采用SCE-UA(ShuffledComplexEvolutionAlgorithm)算法[7]，该方法综合了随机搜索算法、聚类分析法及生物竞争演化等方法的优点，收敛速度较快，鲁棒性强，稳定性好，为高维非线性参数的全局优化问题提供了高效的解决办法，且无需构建显式的目标函数或者对目标函数进行求导计算，被认为是流域水文模型参数优选中最有效的方法。

SCE-UA算法详细步骤如下所示：

(1)算法参数初始化。若待优化的问题是n维，参与进化的复合形的个数p≥2，则每个复合形所包含的顶点数目m≥n+1，计算样本点的数目s=pm。

(2)随机产生样本点。由于缺少先验信息，采用均匀抽样在可行空间随机抽取s个样本点，分别记为x1，x2，…，xs，并计算每一个点si的函数值，记为fi=f(xi)，其中i=1,2,…,s。

(3)样本点排序。把得到的s个样本点按目标函数值升序排列，以数组形式(xi,fi)记录，其中i=1,2,…,s；f1≤f2≤…≤fs，并存入数组空间：D={(xi,fi),i=1,2,…,s}，i=1代表了目标函数值最小的数组。

(5)复合形演化。依据竞争的复合形演化算法分别对各个复合形进行演化。

(6)复合形混合。把进化后的每个复合形A1,A2,…,Ap的所有顶点组合成新的点集，存入数组空间D中，并对D按目标函数的升序进行排序。

(7)收敛性判断。若达到收敛条件则停止，否则返回第(4)步。

在进行参数优化时，将率定期五场降水综合考虑，以径流深相对误差为核心，采用表3所示目标函数，通过SCE-UA算法，自动寻找到使目标函数值达到最小，且满足单场次降水径流深相对误差在20%范围内的最优参数组。

4.2 自动率定结果

SCE-UA算法自身包含多个参数，算法参数取值[8,9]见表4。参数优化的可行域与表4-1所示相同。

通过拉丁超立方体抽样方法抽取42组参数，对率定期五场降水综合考虑，最大迭代次数T分别设置为100、200、500、1 000、2 000、5 000、10 000，并分别连续运行五次，并初步率定出一组较优参数，结果见表5。此时，总目标函数值以及单场次径流深相对误差值见表6，此时SCE-UA算法总目标函数值最小，场次径流深相对误差均在20%以内，满足要求。

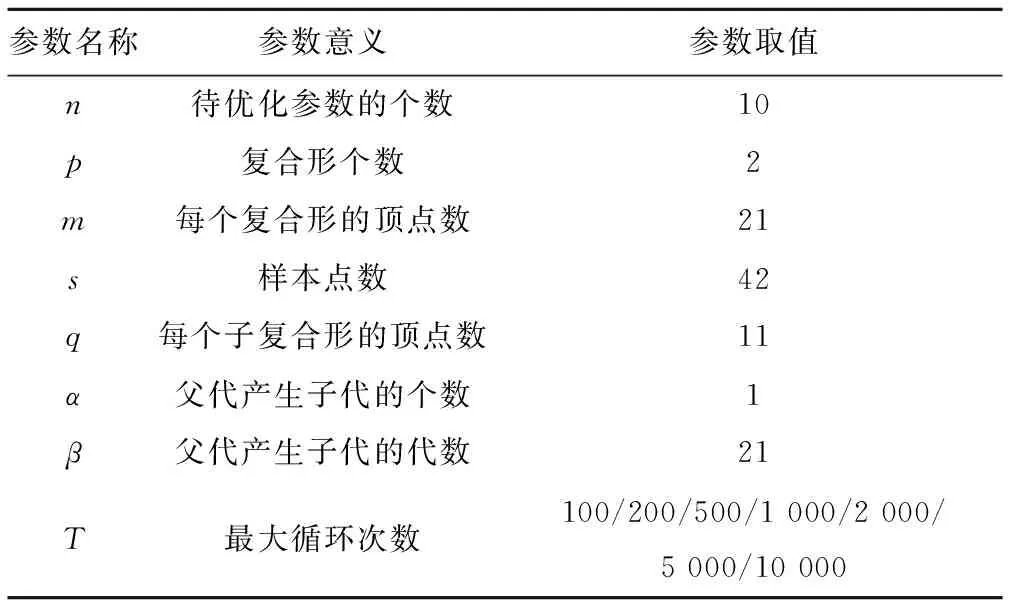
表4 SCE-UA算法参数设置Tab.4 SCE-UA algorithm parameter setting

表5 模型参数初步率定结果Tab.5 Initial rate determination of model parameters

表6 初步率定目标函数值及单场次径流深相对误差Tab.6 Preliminarily rate determination objective function value and relative error of single runoff depth

4.3 参数人工率定与自动率定相结合

模型参数优化的结果不仅依赖于参数的取值范围，参数的敏感性对其也有较大影响，敏感参数通过自动寻优较容易得到最优值，但是不敏感参数容易在“不敏感区间”中陷入次优，导致结果的不确定性。

本文在SCE-UA参数优选过程中，发现蒸发计算与两水源划分参数，即K1、C、WUM、WLM、FC2波动比较大；产流计算参数FC1、WDM相对比较收敛；产流计算参数K2、B1、B2较稳定。其中K1、C、B1、B2为不敏感参数，在率定过程中，可以对K1取多次寻优结果的平均值0.75；C根据经验可以取0.17；B1、B2取自动率定结果值，分别为0.3和0.2。

结合赵人俊提出的客观优化理论[10]，不仅以径流深相对误差为评价指标，还需考虑地下水位相对变化与土壤含水量变化过程线，提高模型的模拟精度。地下水位主要受地下径流的影响，着重调节FC1与FC2使地下水位变化过程线满足要求；K2、WUM、WLM、WDM与土壤含水量有密切关系，调节这四个参数使土壤含水量评价指标满足要求。自动率定与人工率定结合得到的参数数值见表7。

表7 模型参数率定结果Tab.7 Model parameter rate determination result

5 模型适用性评价

5.1 评价指标

产流计算的准确度与可信度是进行排涝模数计算的保障，选取径流深相对误差作为水量平衡评价指标，选取地下水位相对变化量与土壤含水量变化量的相对误差Re和Nash效率系数Ens为指标，共同评价模型模拟精度。一般认为，误差控制在±20%以内，Ens>0.6时模拟结果较好，模拟精度越高，误差越小。计算公式为：

(23)

(24)

式中：Re表示水文要素的相对误差；Sobj表示总径流深(地下水位总相对变化量/土壤含水量总变化量)的实测值，mm；Ssim表示总径流深(地下水位总相对变化量/土壤含水量总变化量)的模拟值，mm；Ens表示Nash效率系数；Si,obj为实测地下水位相对变化量(土壤含水量变化量)序列，mm；Si,sim为模拟地下水位相对变化量(土壤含水量变化量)序列，mm；n为序列长度。

5.2 评价结果

研究中对地下水位相对变化量和土壤含水量使用Nash系数、相对误差来评价，水量平衡校核即模拟径流深使用相对误差来评价。模型评价指标分析见表8。

由表8可知，农田小区的率定期与验证期地下水相对变化量与土壤含水量的 效率系数均大于0.6，各项相对误差均控制在20%之内，模型适用性较好。

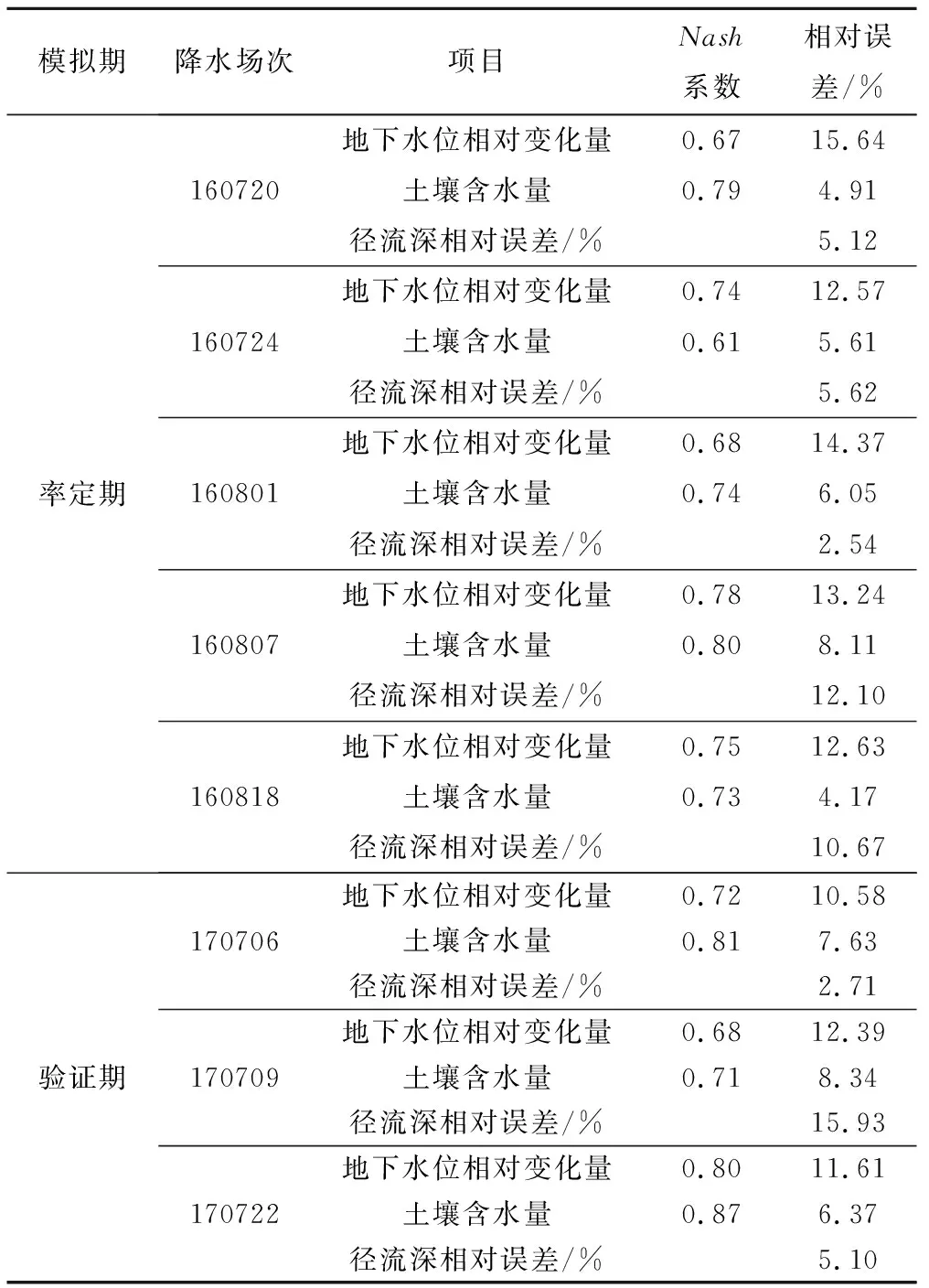
表8 模型评价指标分析Tab.8 Model evaluation index analysis

6 模型检验

6.1 模型检验方法

为了进一步验证构建的产流模型，分别采用单一的超渗产流模型、蓄满产流模型以及已构建的超渗-蓄满垂向耦合模型进行计算，计算模型相对有效性。计算公式如下：

(25)

(26)

式中：CEFc代表超渗-蓄满垂向耦合产流相对于超渗产流的有效性；CEFx代表超渗-蓄满垂向耦合产流相对于蓄满产流的有效性；R0为实测降水径流深，mm；Rc、Rx、RH分别为用超渗、蓄满和超渗-蓄满垂向耦合模型计算的降水径流深，mm。

6.2 模型检验结果

按照公式(25)、(26)选取八场降水计算垂向耦合模型相较于单一超渗模型和单一蓄满模型的有效性，结果见表9。

由表8可知，超渗-蓄满垂向耦合模型相对于超渗产流的有效性为0.869，相对于蓄满产流的有效性为0.912，进一步证明了在农田小区采用超渗-蓄满垂向耦合产流模型是合理的。

表9 三种产流模型下产流结果计算成果表Tab.9 Calculation results of runoff yield under three kinds of runoff models

7 结 论

通过农田产流模型构建及检验，证明超渗-蓄满垂向耦合产流模型应用于华北平原地区是合理的，主要结论如下：

(1)产流模型的敏感性参数为：上层土壤蓄水容量、下层土壤蓄水容量、深层土壤蓄水容量、上层稳定下渗率、土壤缺水量灵敏度系数、下层土壤稳定下渗率。

(2)通过自动参数率定与人工率定结合法，得到优选参数，模拟结果的有效性系数均在0.6以上，相对误差均在±20%之内，说明模型精度较高，模型具有较好的适用性。

(3)通过与单一模型对比检验，超渗-蓄满垂向耦合模型相对于超渗产流模型的有效性为0.869，相对于蓄满产流模型的有效性为0.912，说明超渗-蓄满垂向耦合模型相对单一模型具有更高的模拟精度，也进一步证明了超渗-蓄满垂向耦合产流模型的合理性。

□