基于判别分析的空中目标作战意图识别*

尹 翔,张 萌,陈梦乔

(陆航驻203所军事代表室,西安 710038)

0 引言

空中目标作战意图识别是网络中心战中战场态势评估与指挥决策的重要内容。在网络中心战中。大量飞行器集结于空中,单纯依靠指挥员的作战经验对空中目标的作战意图进行识别已经难以适应网络中心战的要求,必须研究辅助指挥员识别敌方作战意图的技术。目标作战意图识别需要在认知层对信息进行提取与处理,多采用基于军事领域知识、模拟人脑思维的符号推理,研究难度大。多种技术理论,如计划识别理论[1]、支持向量机[2]、D-S证据理论[3]、黑板模型[4]、专家系统[5]、贝叶斯网络[6-7]等已经被用于解决该问题。各种方法都有自己的优缺点,例如计划识别理论灵活性不足,不能处理计划外的行动序列;贝叶斯网络虽然以概率理论为数学基础,但在应用中先验概率与条件概率的取值困难等等。文中主要研究地面防空作战中的空中目标作战意图识别问题。首先,对空中目标作战意图识别问题进行分析,提取空中目标作战意图识别特征向量[8],建立意图知识与规则样本库,对空中目标作战意图识别问题建立数学模型;其次,对数学模型采用判别分析方法进行求解;最后,通过计算机仿真对文中的方法进行验证,并对结果进行分析。

1 空中目标意图识别问题建模

敌方的作战意图不能直接观测,需要根据目标行为、状态及属性进行推断。目前主要依靠军用探测器,如雷达、电磁无源探测器、红外探测器、激光探测器、卫星、声纳[9-11]等等,可以获取目标的位置信息及属性信息。由于战场中目标的信息冗杂,需要在专家知识与经验的基础上从众多类型的信息中选取进行目标意图识别所需的信息,建立反映目标特征的信息向量,可称之为特征信息向量X。

y=F(X)
X=(x1,x2,…,xn),y∈Y={y1,y2,…,ym}

(1)

式中:X为目标的特征信息向量,x1,x2,…,xn分别表示目标不同特征的信息;Y为目标作战意图集合,y1,y2,…,ym表示目标不同类型的作战意图;F为识别规则。识别规则F是目标特征信息向量X与目标作战意图y之间的映射,这种映射具有高度非线性和不确定性。通过对敌方战前的训练、演习及战争初期的作战行动进行统计,建立作战意图知识与规则库[12]:

(2)

B={B1,B2,…,Bm}

(3)

2 判别分析方法

2.1 Fisher判别法

Fisher[13]判别函数通常采用线性函数。假设有m个作战意图总体B1,B2,…,Bm,其均值向量为μ1,μ2,…,μm,协方差矩阵为Σ1,Σ2,…,Σm,当各个总体的均值与协方差未知时,就需要用样本进行估计。Fisher判别采用线性函数表示:

f(X)=Xa′=a1x1+a2x2+…+anxn

(4)

式中a为判别系数向量。显然,要求线函数f(X),只需求出a的值。假设从各个总体中抽取了样本容量为n1,n2,…,nm的m个样本,则经过计算样本的组间离差阵C为:

(5)

样本组内离差阵E为:

(6)

(7)

为了使L(a)最大,对a求偏导数令其为0。采用拉格朗日乘数法,一般认为aEa′=1,则可得:

(E-1C-λI)a=0

(8)

根据特征根与特征值理论,判别系数向量矩阵a为矩阵E-1C的特征值λ所对应的特征向量。将特征根从小到大排列:λ1≥λ2…≥λr,求出r个特征向量a(1),a(2),…,a(r),可得r=min(k-1,n)线性Fisher判别函数:

f1(X)=Xa(1)′,f2(X)=Xa(2)′,…,fr(X)=Xa(r)′

(9)

对于每一个判别函数都必须给出一个用以衡量判别力的指标pi(方差贡献率),定义为:

(10)

s个判别函数f1,f2,…,fs的判别能力指标为cpi(累积方差贡献率),定义为:

(11)

通常当s使得cpi≥85%,可认为前面s个判别函数就够了。将各总体的样本均值向量代入前s个判别函数,可得:

(12)

则m个总体的样本均值向量在s个判别函数上的取值构成了s维空间中的m个点,可将每个点表示为:

(13)

若有新的待判别样品点为X0,则将X0分别代入s个判别函数有：

(14)

现在可以分别计算f(0)到f(i)(i=1,2,…,m)的马氏距离或欧式平方距离,然后再根据距离判别中距离最近的原则判定X0来自哪一总体。

马氏距离计算方法如下:

i=1,2,…,m

(15)

欧式平方距离计算方法为：

(16)

由于马氏距离计算比较复杂,实际应用中都是运用欧式平方距离进行计算。

(17)

2.2 Bayes判别法

Fisher判别法有明显的不足,它与总体各自出现的概率无关,且与错判之后的损失无关。Bayes方法可以解决这两个问题,它对每个总体给出了判别函数。假定已给定一个未知意图的特征信息向量X0,则可以利用贝叶斯公式给出它来自作战意图Bi总体的后验概率为:

(18)

记L(j|i)表示本来是来自总体Bi的样本被错判为来自Bj总体的损失。当j=i时,L(j|i)=0;当j≠i时,有L(j|i)>0。于是可以把原本属于Bi总体的样品X0被错判为属于Bj总体的平均损失定义为:

(19)

(20)

则:

(21)

平均损失最小等价于后验概率最大,即:

(22)

于是判别规则变为:

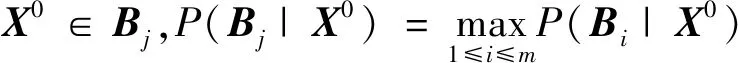
(23)

j=1,2,…,m

(24)

2.3 作战意图识别规则

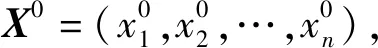
Fisher判别:

(25)

Bayes判别:

i=1,2,…,m

(26)

3 举例

假设敌方对我方某个军事基地实施轰炸任务,我方要对敌方的空中目标进行意图识别。

首先,假定空中目标的特征信息向量X为:

X=(α,r,v,θ,h,σ)

(27)

式中:α为方位角,是指从我方地面军事基地到敌方空中目标方向的方位角,当正北时α=0,顺时针方向一周为6 400 mil;r为距离(km),是指从我方地面军事基地位置到空中目标的距离;v为水平速度(m/s),是指空中目标在水平面上的速度;θ为航向角,是指空中目标飞行的方向,正北为0°,顺时针方向一周分为360°;h为高度(km),是指空中目标距地面的垂直距离;σ为空中目标的雷达反射截面积(m2)。

其次,假设目标的作战意图集合Y为:

Y={y1,y2,y3,y4,y5}

(28)

式中:y1为侦察;y2为攻击;y3为掩护;y4为监视;y5为其它。

因此,n=6和m=5。可知,目标作战意图知识与规则库B={B1,B2,B3,B4,B5},B1是目标意图为侦察的特征信息向量的集合,依此类推。假设目标作战意图知识与规则库B如表1所示。

表1 目标作战意图知识与规则库B

在t时刻,我方探测设备获得了敌方10个未知意图的空中目标的信息,对这些信息处理后得到10个未知意图的空中目标特征信息向量如表2所示。

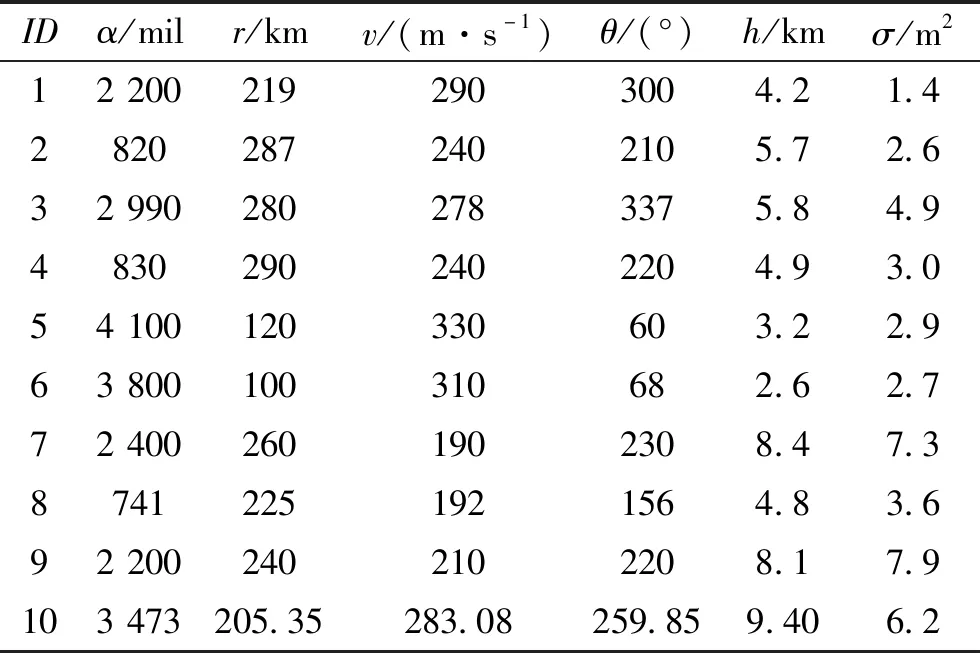
表2 10个未知意图的空中目标特征信息向量

接下来的工作就是采用Fisher判别与Bayes判别建立的识别规则F对10个未知意图的目标进行意图识别。

由表1计算得到5个总体的样本均值向量如表3所示。

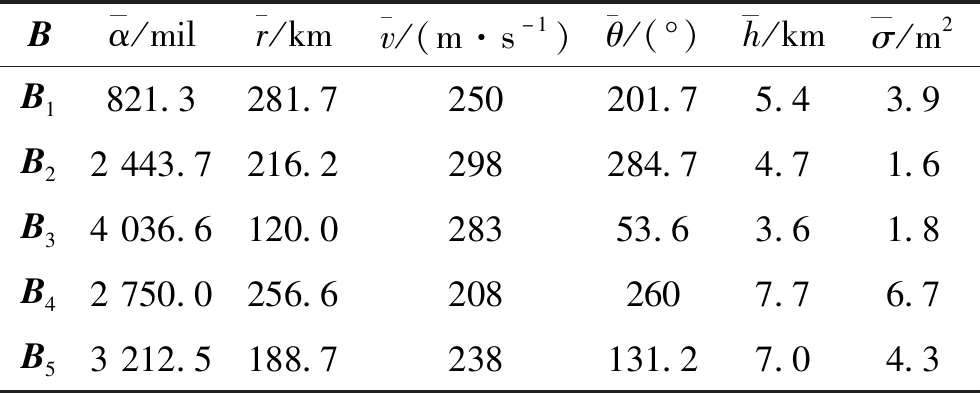
表3 5个总体的样本均值向量

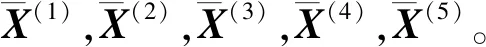
由表1计算得到Fisher判别式为:

(29)

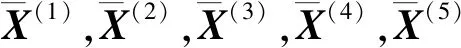
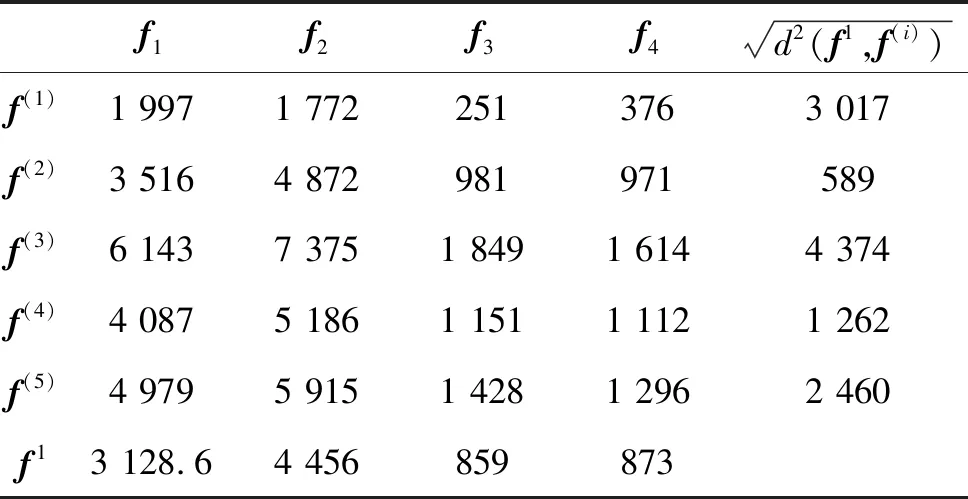
表4 Fisher判别函数值及距离

根据Fisher判别准则:

(30)

下面说明如何采用Bayes判别对未知意图目标的判别方法。由表1计算得到Bayes判别式如式(31)所示。

(31)

将X1代入上式,得到f1(X1)=710.9,f2(X1)=762.2,f3(X1)=730.9,f4(X1)=725.3,f5(X1)=749.2。其中f2(X1)=762.2最大,由Bayes判别准则知i=2,因此对于ID=1的目标的意图为y2攻击,这也与Fisher判别的结果相同。其他9个目标的Bayes判别方法与其相同。

最后给出10个未知意图目标的意图识别结果,如表5所示。

表5 10个未知意图目标的意图识别结果

4 结论

目标意图识别是战场态势评估的重点内容也是难点问题。目标意图识别是在认知层上对多源信息的融合,得到对战场目标的意图判断。文中针对空中目标意图识别问题建立了数学模型,对先验知识采用统计的方法,得到目标作战意图知识与规则库。然后将目标意图识别问题转换为模式识别理论中的分类问题,以Fisher判别与Bayes判别作为分类判别方法,建立目标意图识别规则。最后通过对10个未知意图的目标进行识别,检验文中的思想与方法,证明文中提出方法的有效性。