基于LQR的BTT导弹自动驾驶仪设计*

王广山,王 江

(北京理工大学,北京 100081)

0 引言

早期BTT导弹自动驾驶设计采用古典单输入单输出(SISO)自动驾驶设计方法,其设计思想是忽略三通道间耦合,利用古典控制理论对三个通道独立进行设计,然后在系统中计入协调支路,抵消耦合作用[1-2]。由于BTT较强运动及强耦合,所以大多用现代控制方法进行设计。采用线性二次型最优控制理论进行自动驾驶设计,不仅使设计出的驾驶仪有一定稳定裕度,而且在求出最优控制时,也推导出了对应自动驾驶仪的结构。进行BTT导弹驾驶仪设计时,对三通道响应时间比值进行合适选取,有助于减小通道间耦合,采用线性二次型最优控制理论在设计各通道自动驾驶仪响应时间比值时,可以通过改变权矩阵Q和R来改变求得增益矩阵,从而改变响应时间,这在设计各通道响应时间时具有一定灵活性。

1 BTT导弹数学模型

在小扰动线性化假设条件下,对弹体模型动力学方程进行线性化,然后进行解耦。解耦时要注意滚转角速度ωx变化较大,侧滑通道的耦合项ωxα不可简单忽略[3]。解耦后BTT弹体模型为:

俯仰通道:

(1)

偏航滚转通道:

(2)

(3)

2 线性二次型最优控制介绍

LQ问题是线性二次型最优问题的简称,描述为给定连续时间线性时变受控系统。

t∈[t0,tf]

(4)

给定相对于状态x(t)和控制u(t)的二次型性能指标:

uT(t)R(t)u(t))dt

(5)

寻找容许控制u*(t),使沿着x0出发的相应状态轨迹x(t),性能指标取极小值。LQ问题可分“最优调节器问题(LQR)”和“最优跟踪问题”,最优跟踪问题是LQR问题推广,并可转化为等价LQR问题。

对于无限时间时不变LQR问题,目标函数为:

(6)

式中：(A,B)完全能控,(C,A)完全能观;x为n维状态,u为p维输入且不受限制,A为n×n矩阵,B为n×p矩阵,C为n×n满秩矩阵;Q=QT≥0,为n×n半正定常数矩阵;R=RT>0,为p×p正定常数矩阵。构造Hamilton函数[4]为:

(7)

最优控制应使H取极值,假定u不受限制,求Hamilton函数关于u的偏微分,最后得到:

(8)

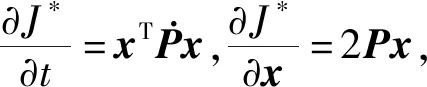
(9)

-PA-ATP+PTBR-1BTP-Q=0

(10)

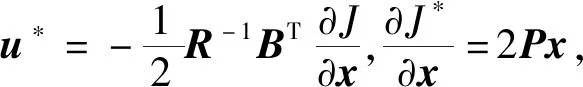
u*=-R-1BTPx=-Kx

(11)

对应的状态反馈闭环系统称为最优调节系统,即：

(12)

标准LQR输出方程中并没考虑Du,当加入该项后,按照上面步骤可推导得[5]:

(13)

3 自动驾驶仪设计

下面设计自驾仪用到的是LQ“最优跟踪问题”,其可转化为等价的LQR问题。

3.1 各通道驾驶仪响应时间比确定

(14)

根据上面LQR最优推导过程可得到:

(15)

滚转通道采用两回路滚转驾驶仪,三通道设计完后,引入运动学耦合项,选取滚转响应时间为俯仰通道1倍、4倍,给出滚转驾驶仪指令为γc=45°,俯仰过载指令ayc=10 m/s2,偏航过载指令azc=0 m/s2进行仿真,通过图1看出滚转相应速度越快,侧滑角越小,可减小通道间耦合。

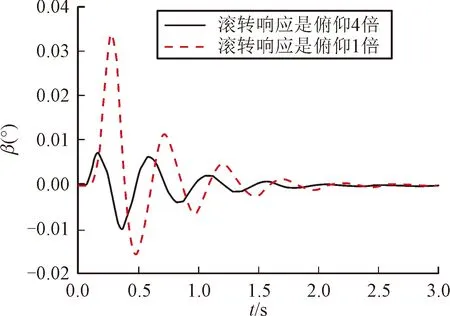
图1 侧滑角响应曲线

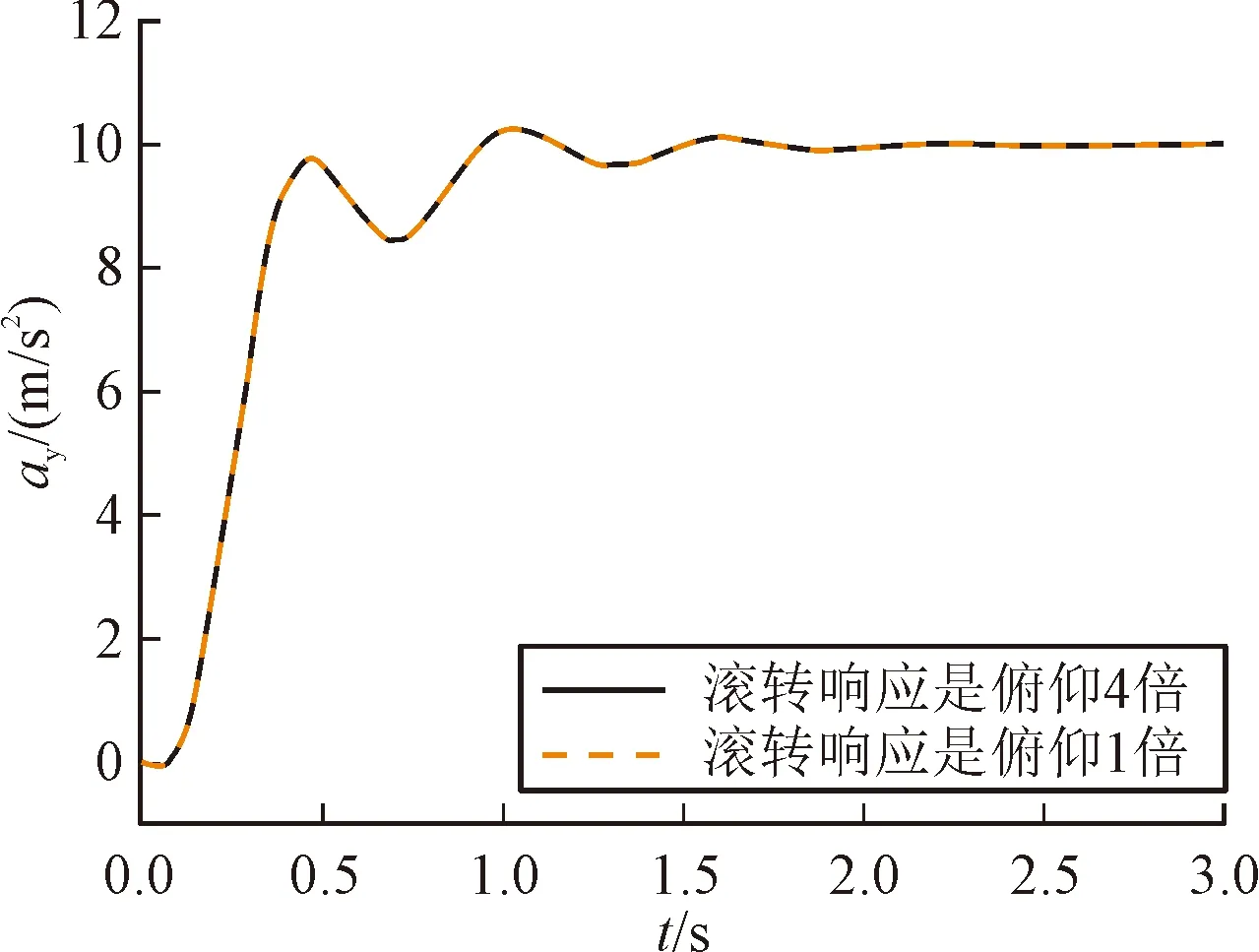
图2 加速度响应曲线

将滚转通道响应速度设为俯仰4倍,改变Q11、R11调节偏航通道响应时间,使偏航通道响应时间依次为俯仰通道1倍、4倍,取γc=45°,ayc=10 m/s2,azc=0 m/s2进行仿真,从图3可看出,偏航响应速度越快,侧滑角越小,相应的耦合也就越小。根据仿真结果,将偏行通道响应时间设为俯仰的3倍,滚转相应时间设为俯仰的4倍。

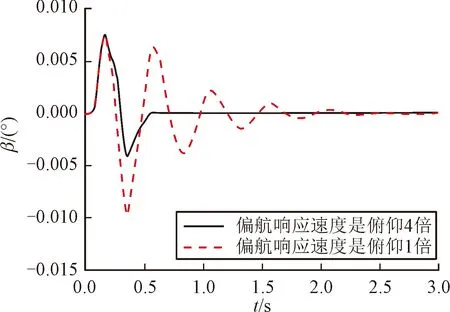
图3 侧滑角响应曲线

3.2 俯仰通道过载自动驾驶仪设计

根据“最优跟踪问题”,俯仰状态方程如下:

(16)

性能指标为:

(17)

求得:

(18)

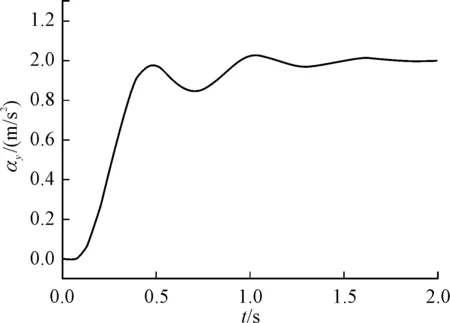
图4 俯仰加速度响应曲线

由上式看出线性二次型最优控制求出的是经典三回路过载驾驶仪的控制律。取Q11=0.01,R11=2 500,求得状态反馈增益阵K,各增益为ωI=0.128 3,Ka=0.001 9,KDC=1.071 5,Kg=0.042 7,通过仿真得到加速度响应上升到稳态值63.2%时的时间为0.3 s,幅值裕度为19.7 dB,相位裕度为63°。

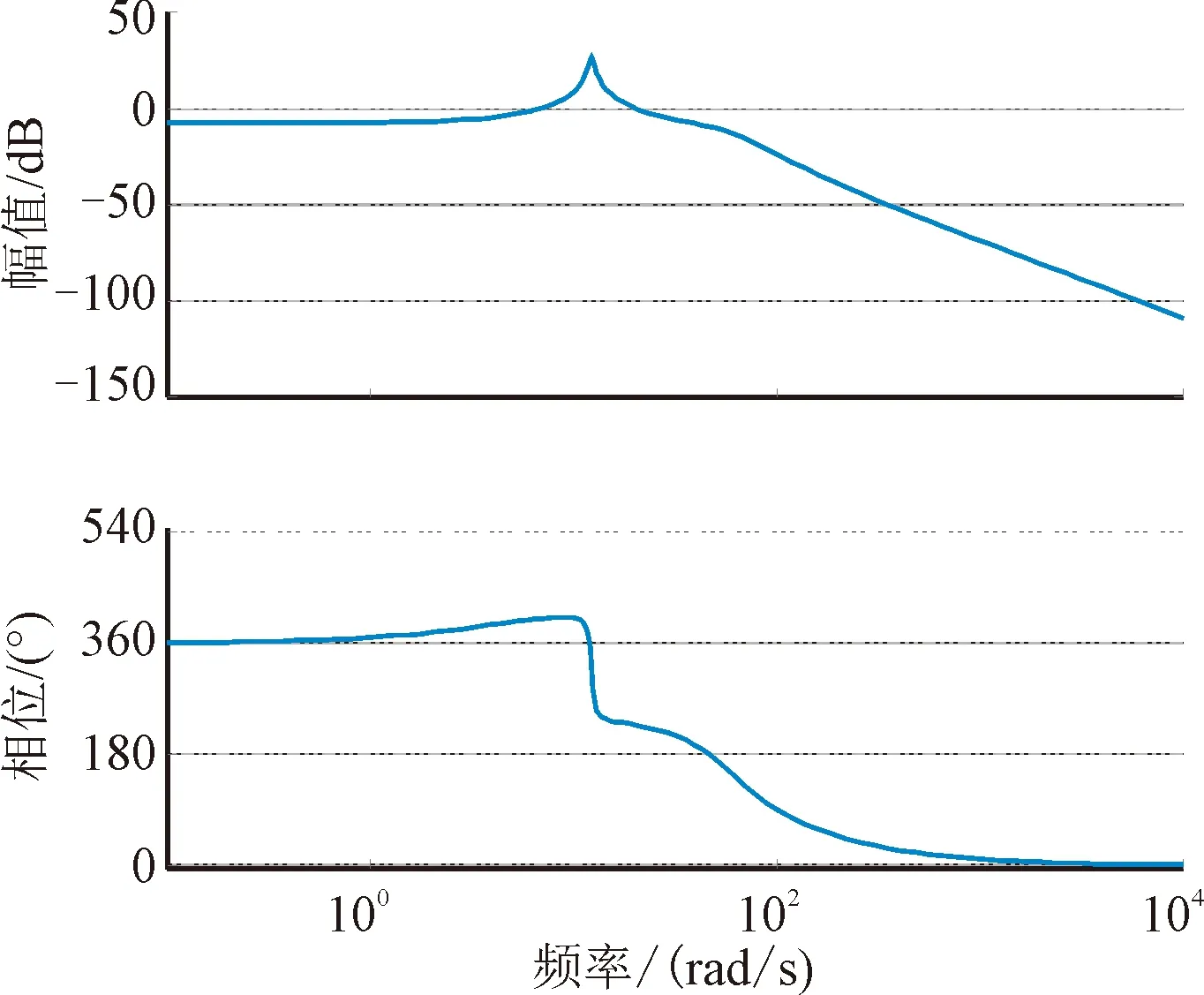
图5 开环伯德图

3.3 偏航通道过载自动驾驶仪设计

偏航通道状态方程形式与俯仰通道形式相同,对应的量如下:

L=D(1,:)

(19)

取Q11=0.1,R11=35 000,得增益Ka=0.000 72,KDC=3.637 5,Kg=0.063 4,仿真如图6、图7所示,63.2%上升时间为0.1 s,幅值裕度为9.7 dB,相位裕度为46°。

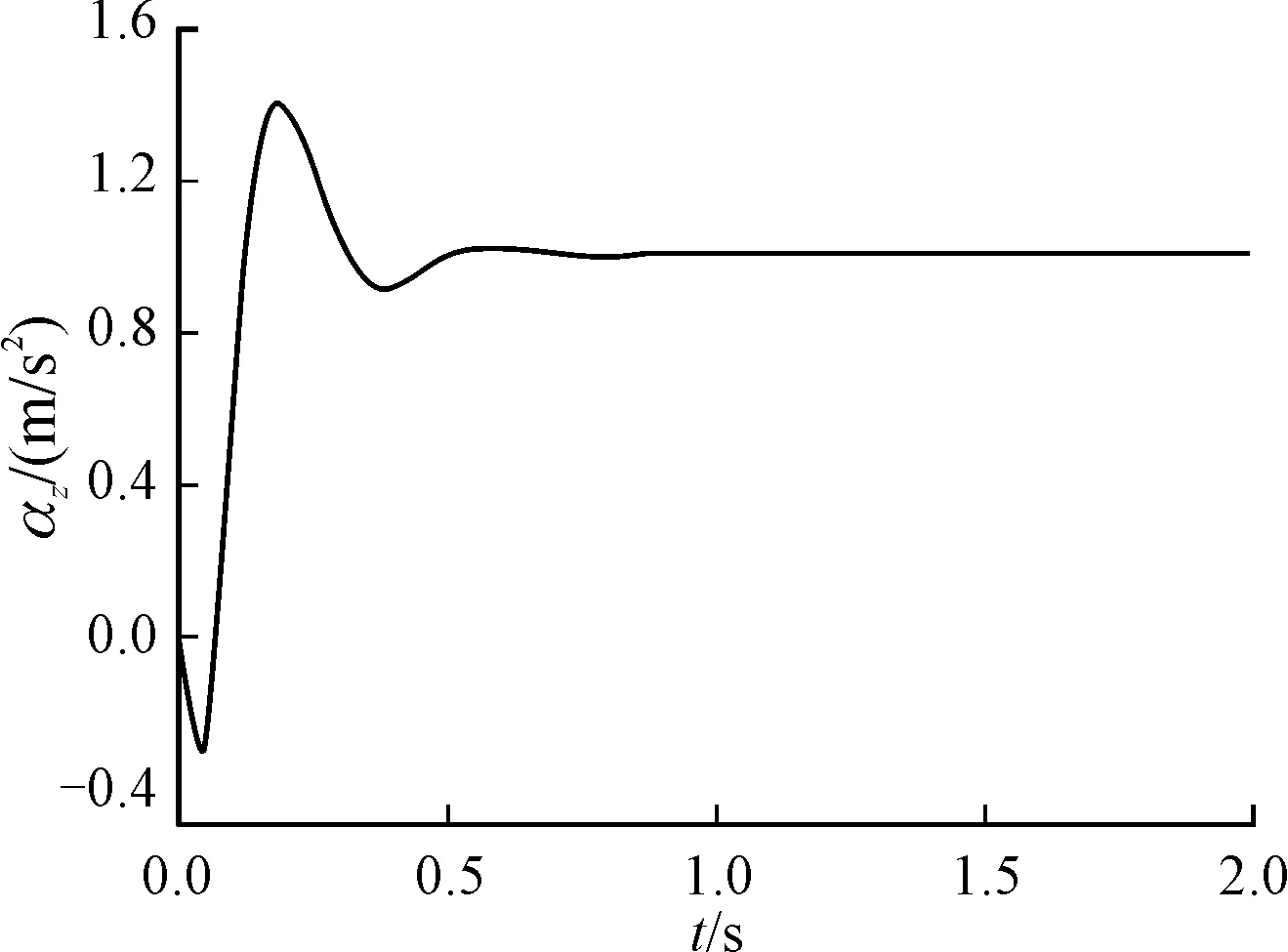
图6 偏航加速度曲线

3.4 引入耦合项仿真

滚转通道采用滚转驾驶仪,用解析法设计[6],设计结果为63.2%上升时间为0.07 s。三通道设计完成之后,在三通道之间引入各耦合项,在给定指令ayc=150 m/s2,γc=45°,azc=0 m/s2条件下仿真。

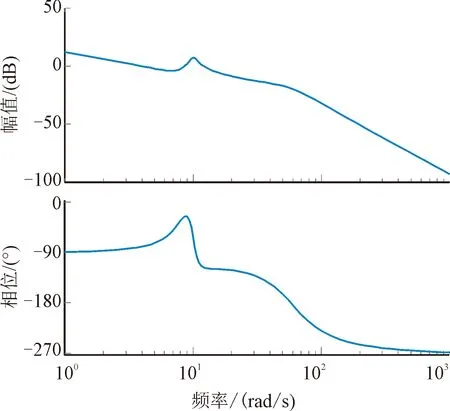
图7 开环伯德图

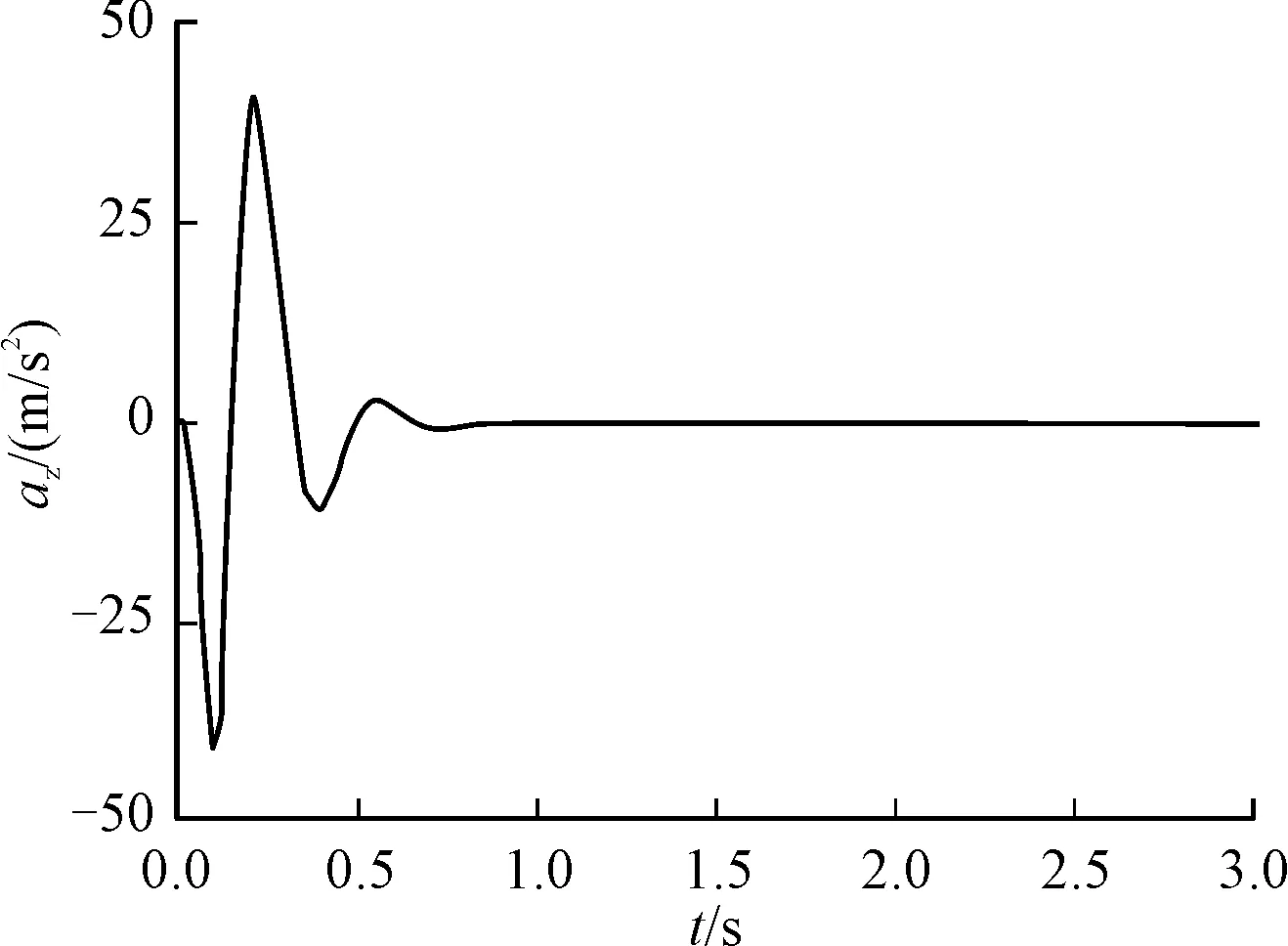
图8 侧向加速度响应曲线

图9 攻角响应曲线

图10 侧滑角响应曲线

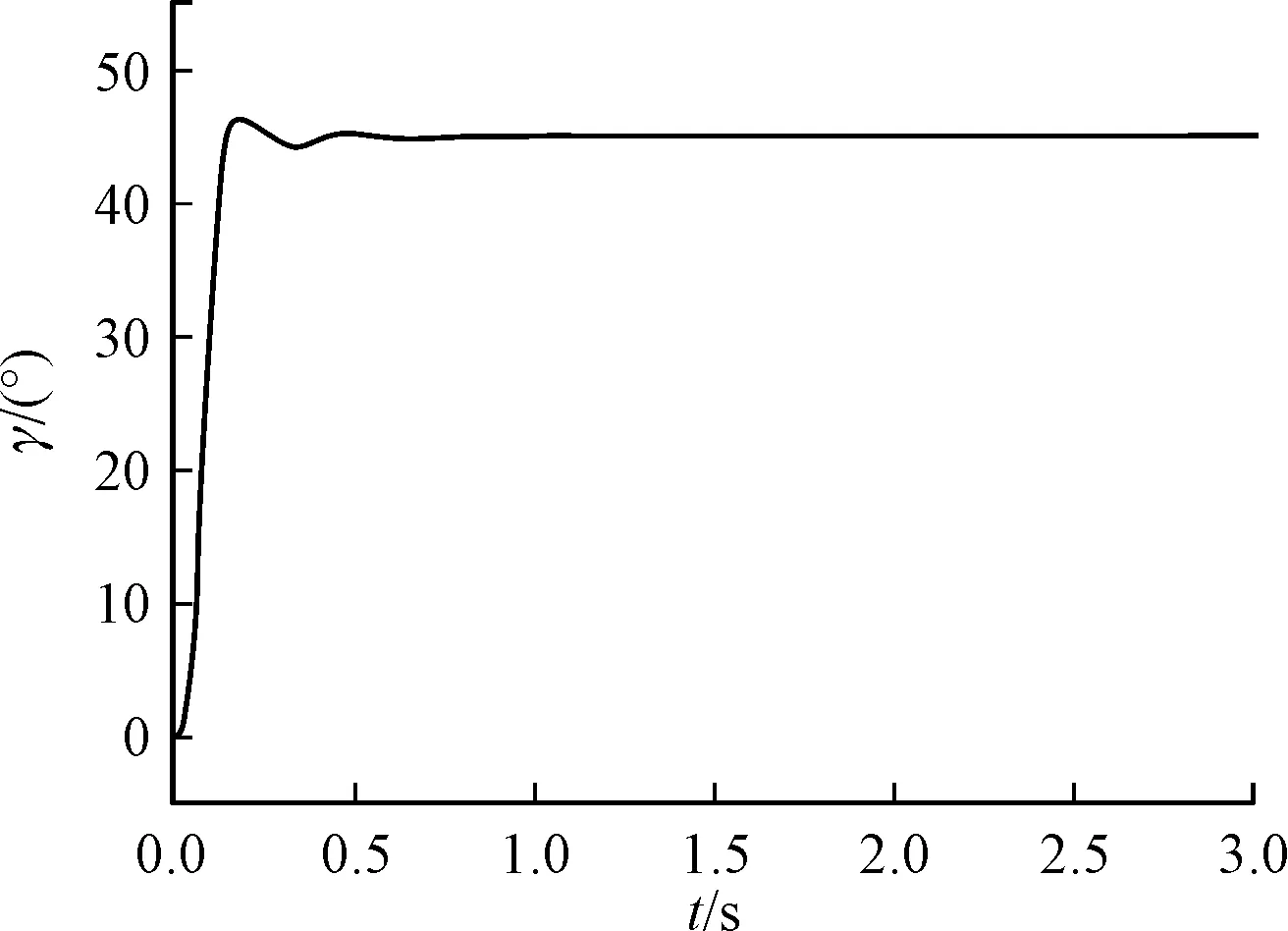
图11 滚转角响应曲线

图12 副翼响应曲线

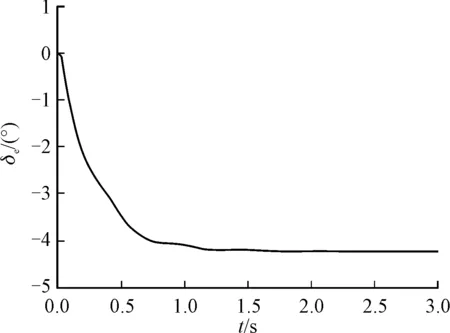
图13 升降舵响应曲线

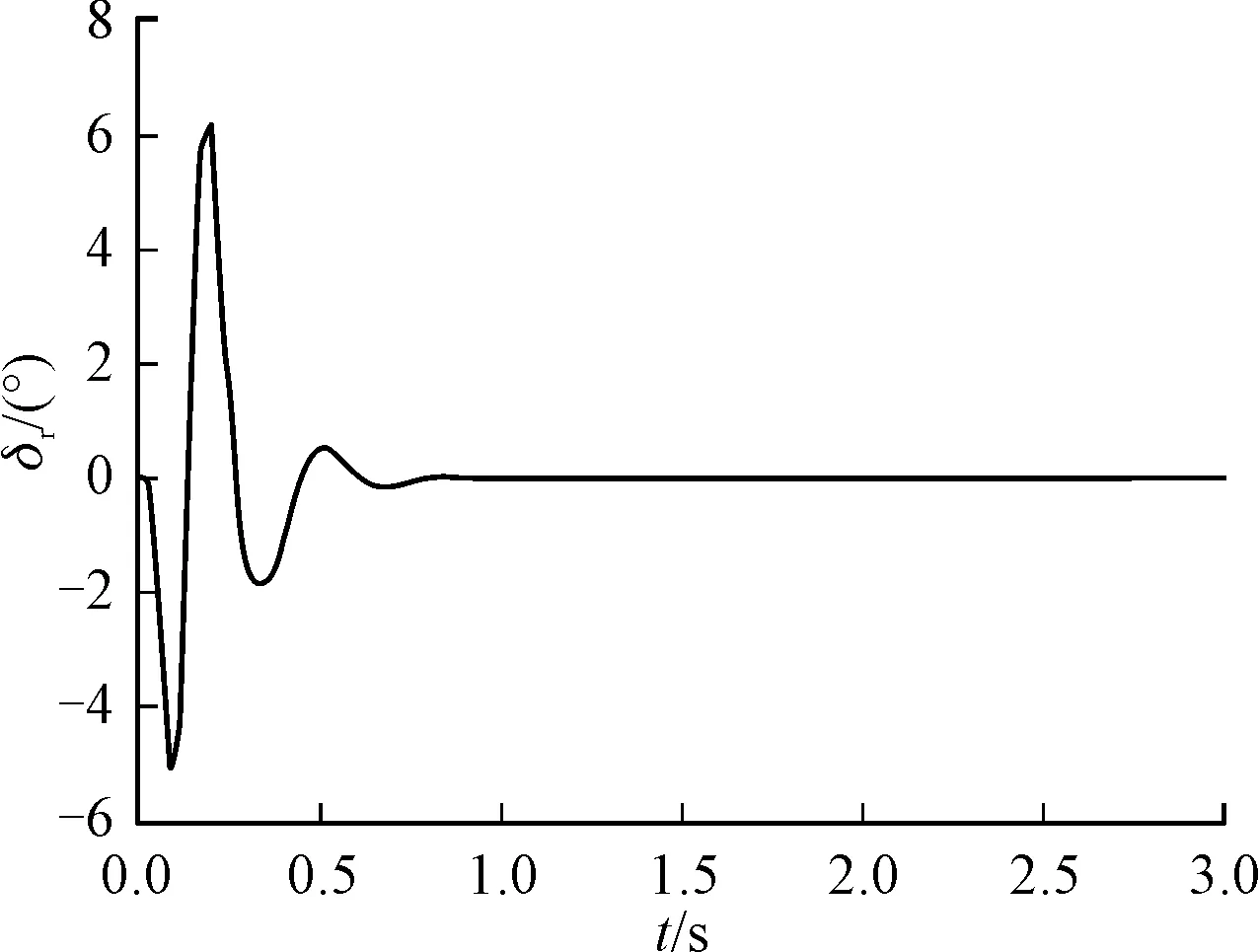
图14 偏航舵响应曲线

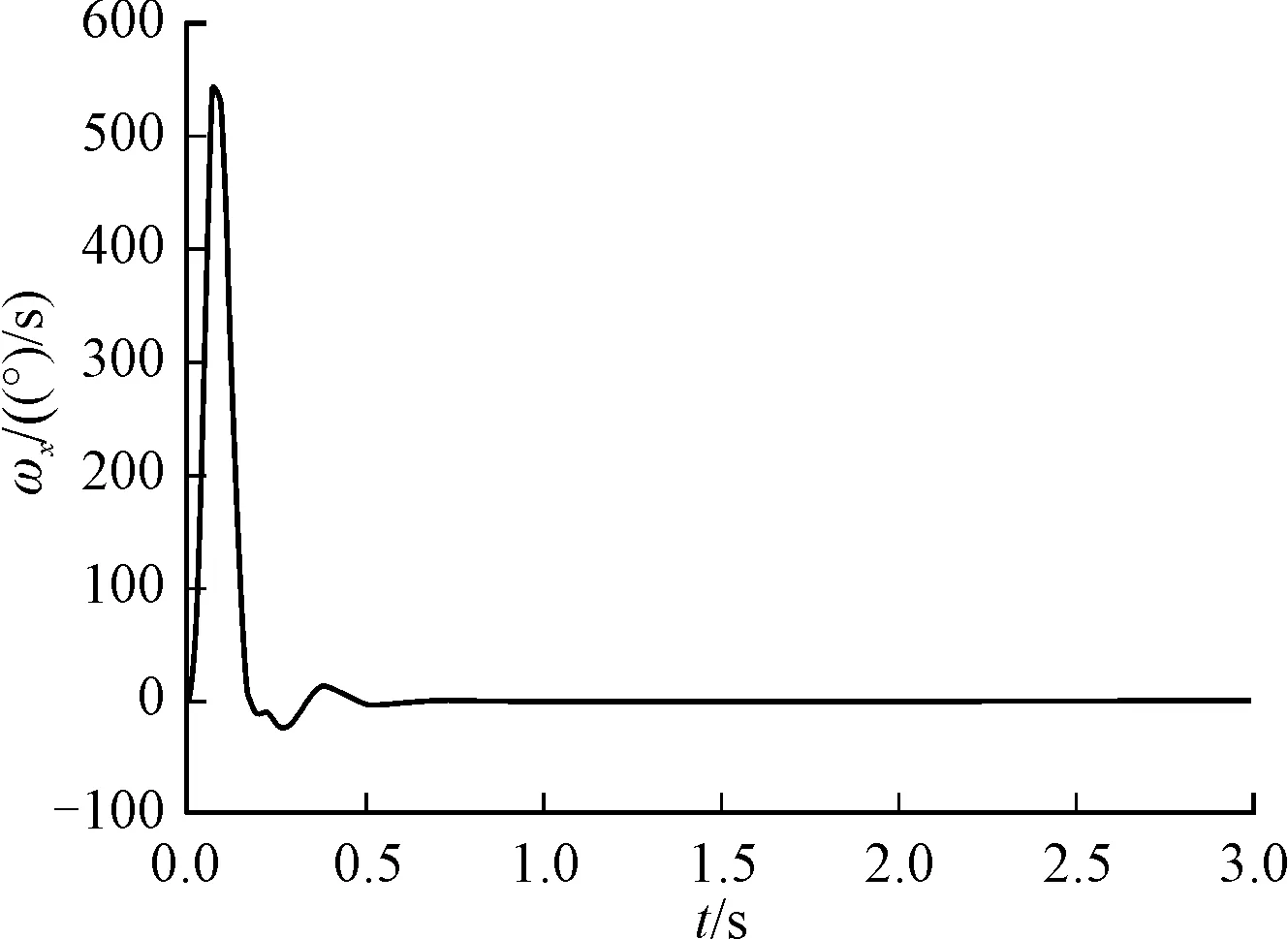
图15 滚转角速度响应曲线

图16 偏航角速度响应曲线

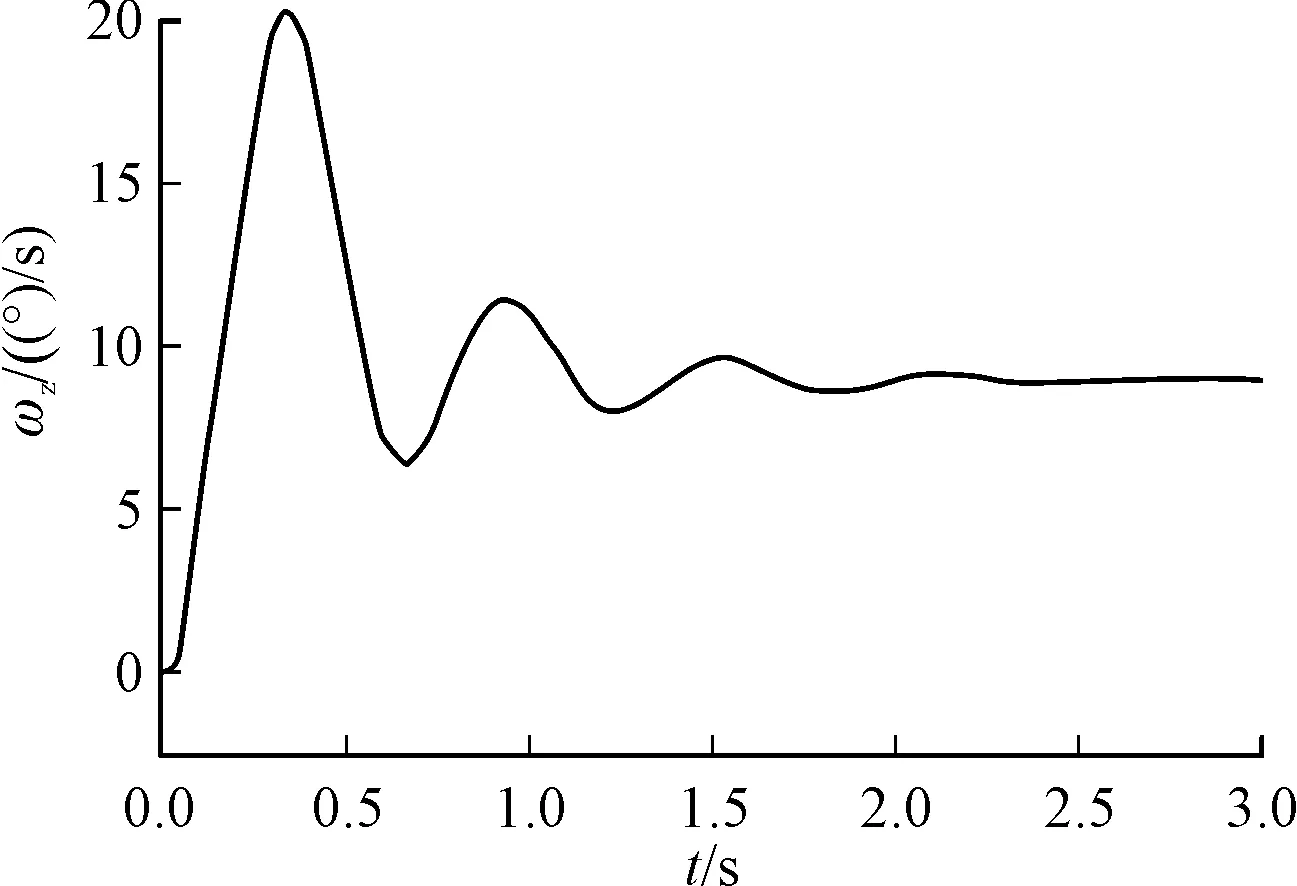
图17 俯仰角速度响应曲线

图18 俯仰加速度响应曲线

4 结论

通过前面仿真可看出采用线性二次型最优控制理论设计的BTT导弹俯仰和偏航通道自驾仪具有一定的稳定裕度。在确定各通道自动驾驶仪响应时间比值时,可以通过改变Q11和R11实现,较古典设计具有一定灵活性,在仿真中可看出滚装通道响应越快,耦合越小,偏航通道响应快对耦合抑制效果较好。三通道设计完成后引入运动学耦合,气动耦合,控制交叉耦合项进行仿真验证,从图中看出跟踪效果较好。但是LQR必须准确测量全部状态量,这也限制其应用。