地磁辅助信息的旋转弹姿态估计方法*

龙达峰,孙俊丽,温晶晶

(1 惠州学院,广东惠州 516007;2 中北大学信息与通信工程学院,太原 030051;3 晋西工业集团有限责任公司,太原 030027)

0 引言

由于旋转弹发射高过载、高速旋转和弹载空间狭小等恶劣弹载环境的限制,适用于旋转弹用的测量传感器主要有MEMS陀螺仪、地磁传感器和GPS等[1-4],而且现有导弹弹载姿态测量系统直接移植于高速旋转弹导航应用时会出现各种问题。特别是弹丸发射时高达10 000g的极大过载,使得弹载姿态测量传感器容易出现短时的饱和失真、性能退化、甚至失效等,造成弹载测量系统的性能严重退化、参数不全或是导航初始参数获取困难等问题[5]。针对弹载姿态测量系统移植应用问题,目前普遍采用对弹体本身进行局部改造以实现测量系统的移植应用,但这些改造方会影响到依靠旋转稳定工作方式弹丸的气动力特性,且造成弹载装置结构变得非常复杂,从而极大地增加了旋转弹智能化改造难度[6]。因此,研制具有易移植、小体积和高精度的旋转弹用姿态测量系统成为其制导化改造的难点所在。此外,在弹载惯导测量系统中,若对低精度MEMS陀螺测量输出角速率的积分解算存在严重的误差累积。考虑到基于地磁信息的磁测姿态系统是通过测量弹体内地磁场矢量信息来确定弹体姿态方法,其测量误差不随时间累积[7-8]。因此,文中提出了一种利用地磁传感器测量信息对惯性测量系统进行组合滤波方法,由地磁传感器、MEMS陀螺和GPS测量弹体姿态信息,再根据所建立的组合滤波模型,由改进EKF滤波算法完成旋转弹飞行姿态准确估计。

1 旋转弹飞行姿态测量方案

旋转弹姿态传感器方案包括三轴地磁传感器和三轴MEMS陀螺仪,分别用于测量地磁信息和弹体角速率信息。文中选取地面发射坐标系作为导航参考坐标系,因此弹体磁测姿态解算公式为:

(1)

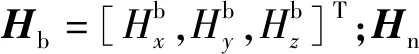
通过对组合滤波模型的可观测性研究分析发现[9-10],若仅仅利用MEMS陀螺输出角速率和地磁传感器输出信息进行弹体姿态滤波估计,3个姿态角是不完全可观测的,解决的方法是借助于其它辅助测量方法获得其中任一个姿态角后再进行组合滤波。考虑到旋转弹外弹道飞行的特殊性,即便是弹丸受控飞行期间,弹丸飞行也是小攻角状态,因此在不考虑弹丸的攻角情况下,完全可以利用GPS所测量的弹体速度信息来估算弹体的偏航角和俯仰角,用于代替偏航角不变假设,其估算原理如图1所示。

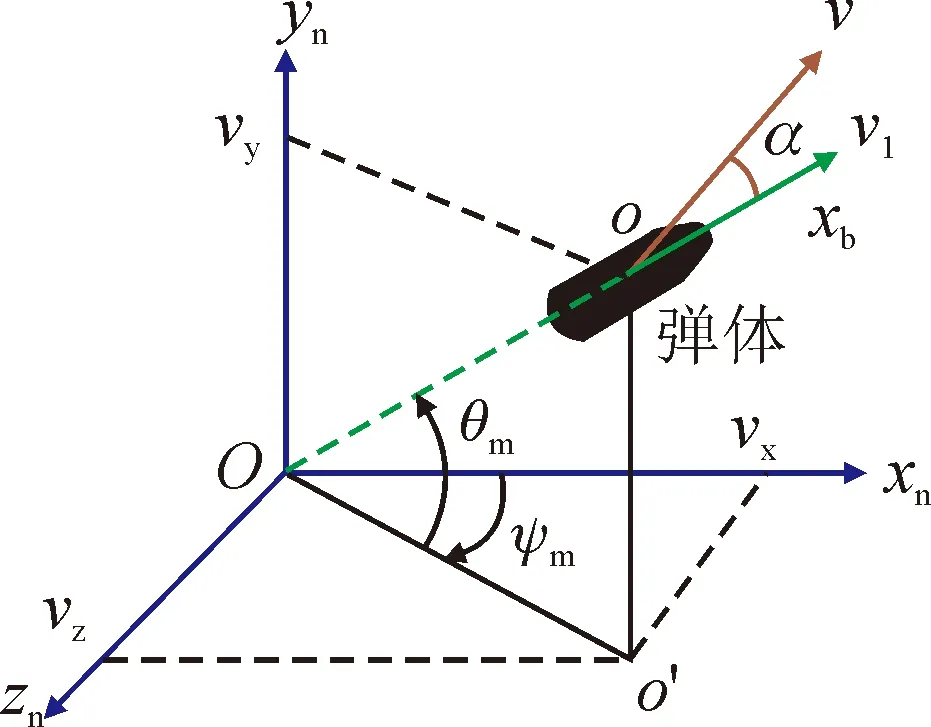
图1 弹丸偏航角和俯仰角估算原理

由图1所示速度投影关系可知,利用GPS测量所得的速度信息来估算弹体偏航角ψm和俯仰角θm姿态公式为:

(2)

式(2)是假设攻角为零的情况下才能完全成立。然而,若旋转弹飞行时攻角较小情况下,仍然可以利用式(2)进行计算,所估算所得偏航角和俯仰角会将存在一定的误差,但其可以当作是测量噪声带来的误差来进行处理,可以通过后续的姿态滤波算法对其进行误差参数估计与数据补偿。

综合上述测量方案,文中采用以磁测信息、弹体速度估算所得偏航角和俯仰角共同作为系统观测信息,对惯性导航系统进行姿态组合滤波估计,最终实现旋转弹飞行姿态的准确测量。

2 旋转弹弹体姿态估计算法

2.1 弹体姿态组合滤波器结构器设计

为了提高弹体姿态算法的实时性,弹体姿态滤波器采用图2所示3个滤波器组成的多速率组合式实时滤波结构。其中磁传感器滤波器和陀螺滤波器分别用于完成弹载地磁传感器和MEMS陀螺角速率测量输出的数据的滤波与误差补偿;旋转弹飞行姿态估计滤波器用于实现弹体偏航角、俯仰角和滚转角三维姿态角的快速滤波估计。

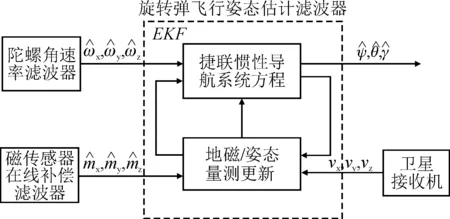
图2 多速率组合式的实时滤波器方案

2.2 地磁传感器误差估计与补偿

弹载地磁传感器用于测量弹体系坐标内的地磁信息,其测量误差主要有零偏、灵敏度误差和交叉耦合误差等[11-12]。因此,采用公式(3)所示的磁传感器误差模型进行地磁传感器测量误差参数在线估计和磁测数据补偿。

(3)

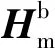
对测量误差模型(3)进行进一步的变换,可推导得到三轴磁传感器测量数据的补偿公式为:

(4)

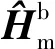
2.3 旋转弹弹体姿态估计滤波器

由捷联惯导原理可知,弹体飞行姿态欧拉方程式为[13-14]:

(5)

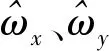
选取弹体偏航角、俯仰角和滚转角作为系统的状态变量Xa=[ψ,θ,γ]T;以弹体飞行姿态欧拉方程式(5)作为状态方程,将其可简写为如下一般形式:

(6)

v(t)

(7)

式中,ci,si(i=ψ,θ,γ)分别为余弦函数cosi和正弦函数sini的简写形式。由于上述观测方程是非线性方程,将其简写为如下形式:

Za(t)=h[Xa(t),t]+v(t)

(8)

因此,由状态方程(5)和观测方程(7)共同构成弹体姿态组合滤波模型。

2.4 改进EKF的弹体姿态滤波算法

考虑到上述所构建的姿态组合滤波模型是强非线性特征,滤波模型的线性与离散化处理时,传统EKF滤波算法实质上是基于一阶近似的线性化方法,在Taylor级数展开关系式中并没有取其余高阶项,只取一阶项,分析发现其会带来较大的系统误差,使得其滤波估计精度有所下降。因此,文中在进行模型的离散化及线性处理时,采用二阶近似方法来降低线性化带来的系统误差,即取到Taylor级数展开的二阶项,通过这样的方法以降低线性化带来的系统误差,为进一步提高EKF算法精度。相比于线性一阶逼近的EKF滤波算法,文中所采用基于二阶近似的改进EKF滤波算法主要不同在于如下两个方程:

(9)

式中：ei为第i个标准基向量,即第i个元素为1,其余为0;tr(·)表示取矩阵的迹,也即为取矩阵主对角元素之和;Hx为观测方程的雅可比矩阵;而Hxx,i为观测方程Hessian矩阵,其计算公式为:

(10)

算法除上述公式不同,二阶近似改进EKF滤波算法与传统EKF滤波算法基本相同,其主要流程也包括初值选取、状态预测与量测更新3个滤波算法步骤,但由于进行Taylor展开时取二阶近似,所以状态预测和量测更新方程有所不同。因此,基于二阶近似改进EKF滤波算法具体步骤如下:

1)滤波初始参数:

2)时间更新过程:

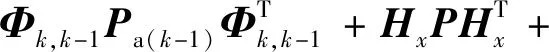
3)量测更新过程:

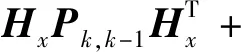
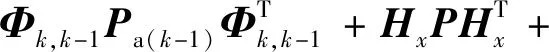
因此,通过上述的初值选取、状态预测与量测更新3个滤波算法步骤,最终完成弹载飞行姿态参数的快速滤波估计。

3 算法的仿真验证

3.1 仿真参数设置

文中选取152 mm高速旋转弹为仿真对象,根据旋转弹外弹道数学模型,首先利用Matlab程序计算机仿真生成外弹道飞行数据以及各弹载姿态传感器测量输出的理想数据。然后,再根据所建立的弹载传感器的测量误差模型,并按如表1所示的弹载传感器误差参数设置,仿真生成弹载传感器的实际测量输出数据,在此基础上进行弹体飞行姿态估计算法的仿真验证。

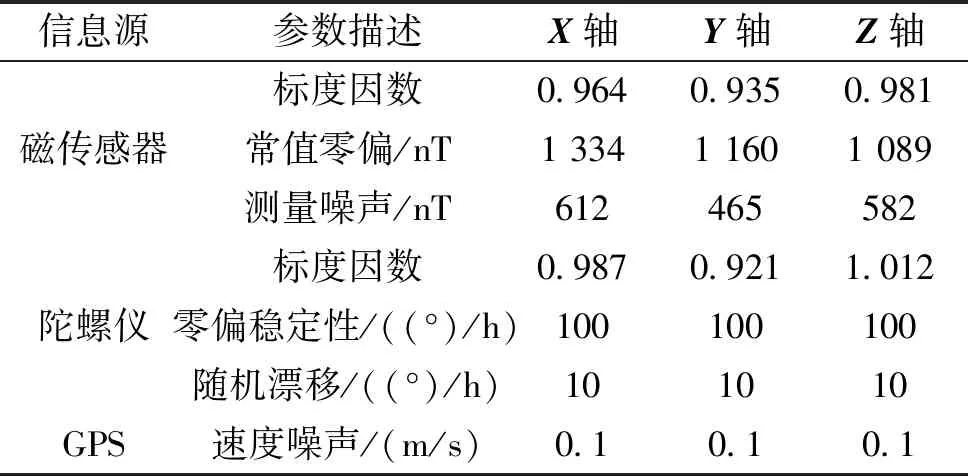
表1 弹载传感器误差参数设置

3.2 数值仿真及结果分析

根据上述仿真设置的条件,旋转弹外弹道飞行轨迹如图3所示。

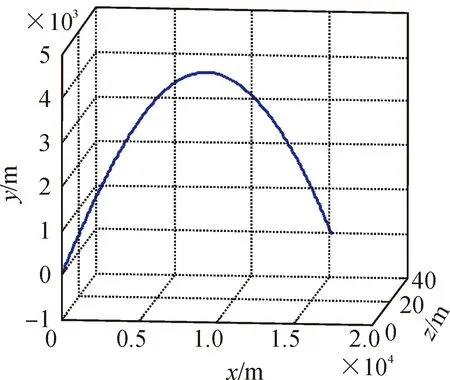
图3 弹丸外弹道曲线

采用前述基于改进EKF的弹体姿态滤波算法完成旋转弹飞行偏航角、俯仰角和滚转角三维姿态的滤波估计,弹体姿态滤波估计结果如图4～图9所示。

图4 偏航角滤波估计结果

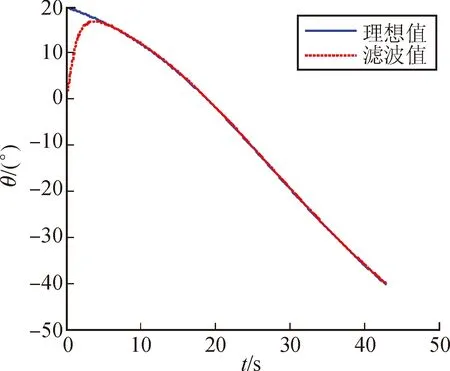
图5 俯仰角滤波估计结果

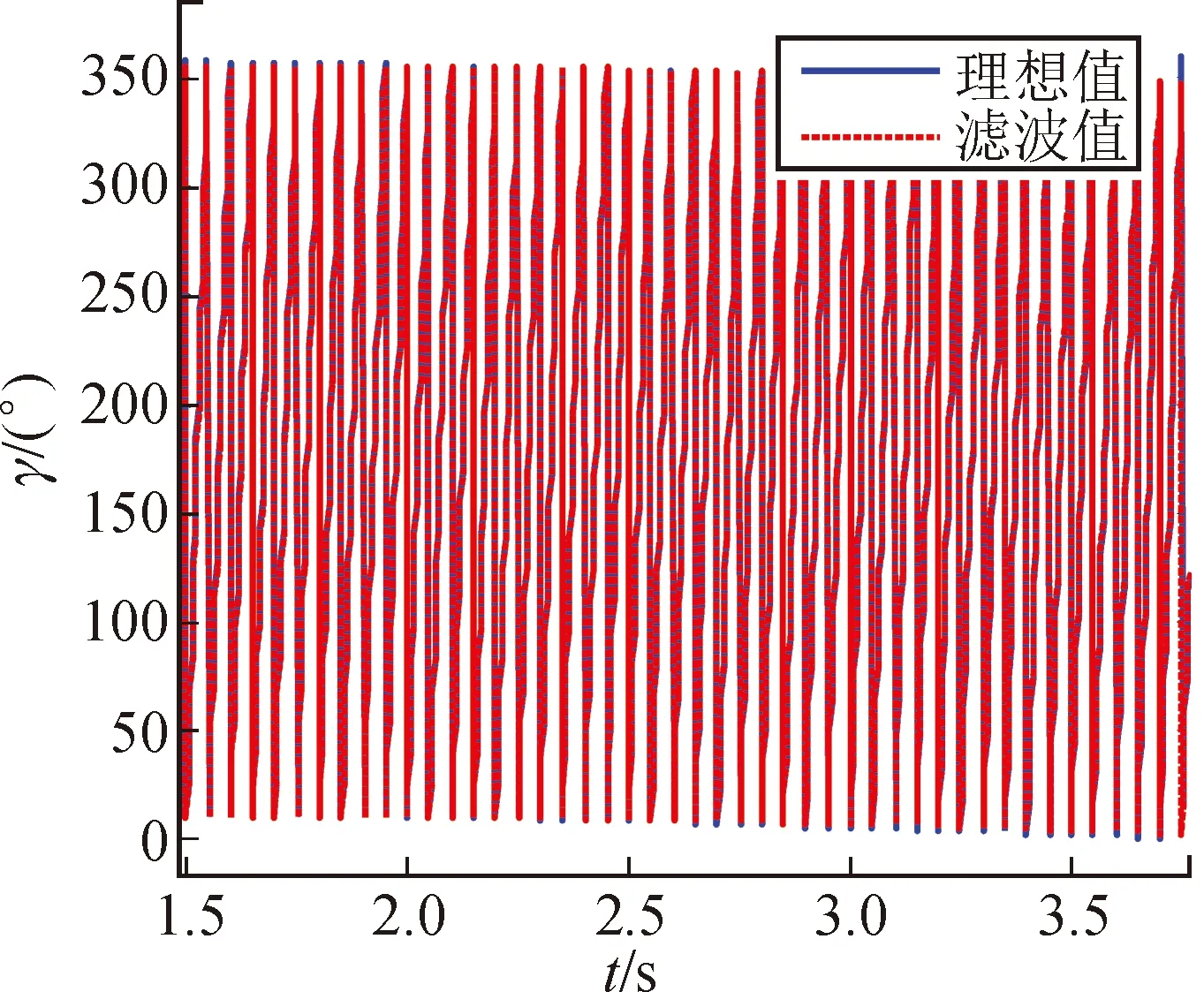
图6 滚转角滤波估计结果

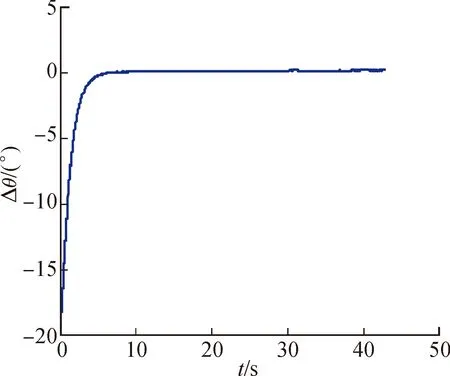
图8 俯仰角估计误差曲线

图4～图6所示分别为弹体偏航角、俯仰角和滚转角的理论值与滤波估计值的结果对比,图中蓝色实线为旋转弹理想弹道条件下的弹体姿态角,而红色虚线所示为弹体姿态算法滤波估计所得三维姿态角,与之相对应的弹体偏航角、俯仰角和滚转角姿态角估计误差如图7～图9所示。

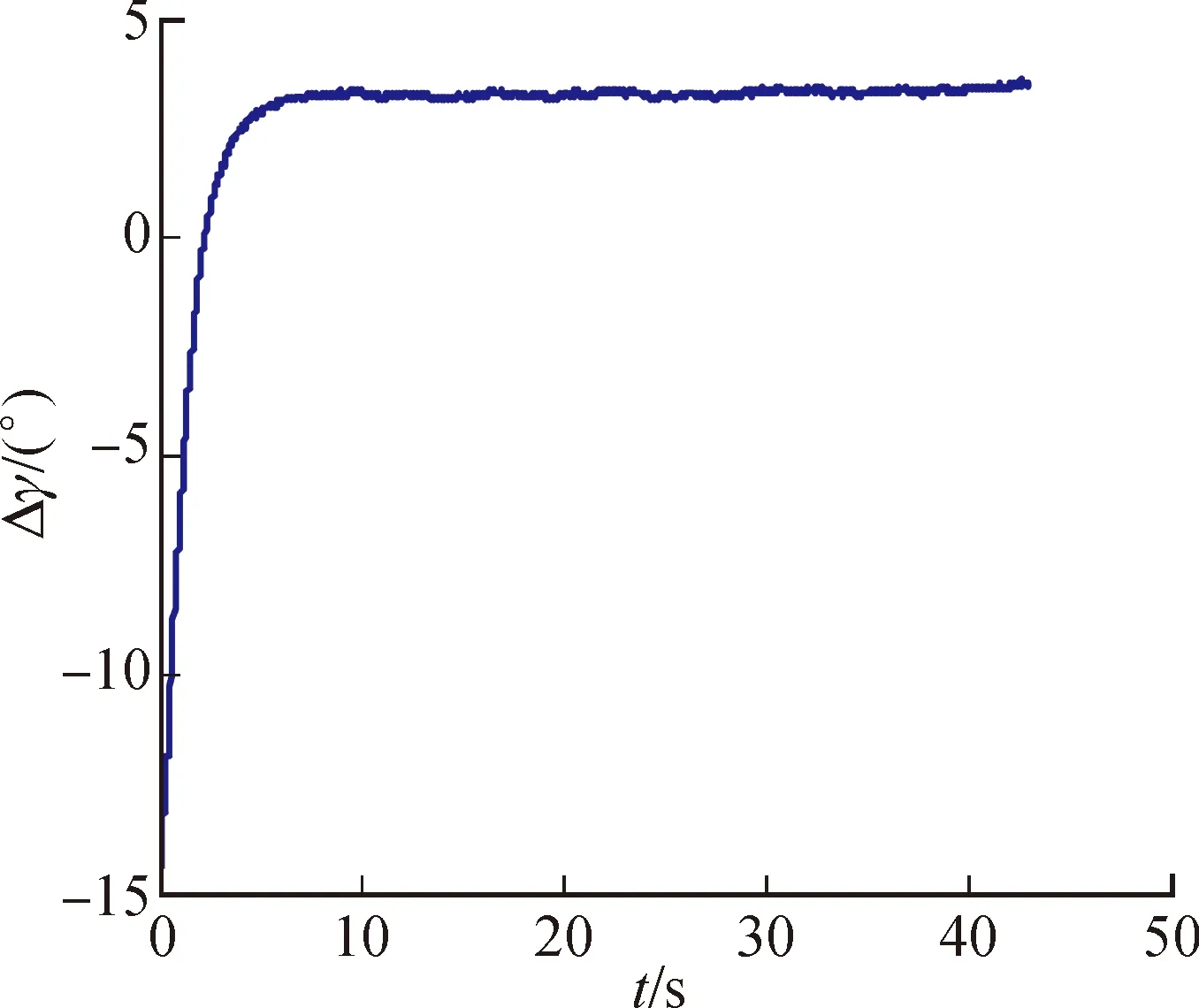
图9 滚转角估计误差曲线

从上述姿态估计结果来看,其弹体三维姿态在5 s内基本能够得到很好的收敛,在滤波稳定后,经统计得弹体偏航角、俯仰角和滚转角姿态估计误差分别为0.806 8°、0.839 2°和3.926 4°(1σ估计误差),结果表明弹体姿态滤波算法可以快速完成弹体飞行姿态准确估计。

4 结论

针对旋转弹飞行姿态测量问题,文中采用地磁传感器、MEMS陀螺和GPS姿态组合测量方案,建立了基于多速率组合式弹体姿态滤波模型,并采用了基于改进EKF的弹体姿态滤波算法完成弹体的姿态估计方法。最后选取152 mm旋转弹为研究仿真对象,利用计算机仿真方法进行了所述算法的仿真验证。仿真结果表明,弹体三维姿态在5 s内能够实现很好的收敛,在滤波稳定后,弹体三维姿态在5 s内能够得到很好的收敛,经统计得弹体偏航角、俯仰角和滚转角3个姿态角估计误差分别为0.806 8°、0.839 2°和3.926 4°,验证了文中所述算法可以快速完成弹体飞行姿态准确估计。