考虑系统不确定性的车辆主动悬架自适应模糊滑模控制
2018-08-27王建平
庞 辉, 梁 军, 王建平, 刘 凡
(西安理工大学 机械与精密仪器工程学院, 西安 710048)
车辆主动悬架能够通过其作动器产生主动控制力来抑制由于路面不平引起的车身振动,并能根据车辆每一时刻运动状态和路面激励产生瞬时不同的主动控制力,使悬架始终处于最优减振状态,进而提高车辆平顺性与操纵稳定性[1-6]。然而,由于悬架系统本身具有诸多非线性因素和模型不确定性,车辆在不同行驶道路条件(路面不平度)和工况(加速、制动和转弯)下,悬架参数会在一定范围内发生变化,这就使得对悬架系统的动态特性难以用精确数学模型来描述,从而造成控制上的困难。因此,在车辆主动悬架控制中,考虑悬架系统模型不确定性具有重要意义。
T-S模型是由Takagi和Sugeno提出的一种模糊推理模型,该模型相当于将输入空间分为若干个模糊子空间,首先在每个模糊子空间建立一个局部线性模型,然后使用隶属函数平滑的将各个局部模型连接起来,从而形成非线性函数的全局模糊模型。由于T-S模糊模型结构简单,对复杂非线性系统可通过一些简单线性子系统的加权和来表示,近年来基于T-S模糊模型的控制方法受到广泛关注[7-10]。文献[11]针对主动悬架系统控制执行器的延迟和故障不确定性等问题,在满足安全性能约束要求并保证系统渐近稳定性和鲁棒性前提下,设计了一种模糊鲁棒H∞控制器。文献[12]综合T-S模糊模型、区间二型模糊推理和吴-孟德尔不确定边界方法构建了一种线性模型控制界面之间的切换策略,同时对该控制策略的稳定性进行了分析。文献[13]针对非线性半车悬架系统建立了T-S模糊模型,设计了一种具有时变输入延迟和输出限制的新型模糊动态输出反馈控制方案。上述文献所设计的T-S模糊控制在非线性模型追踪方面取得了较好控制效果,可很好地获取模型相应信息。但是,对信息简单的模糊处理容易导致控制精度降低及较差的动态品质。因而已有研究人员将模糊控制与滑模控制相结合,并应用于非线性控制系统。例如,文献[14]将滑模控制与单输入单输出模糊逻辑控制器结合,设计了一种用于非线性半车模型的主动悬架无抖振模糊滑模控制器。文献[15]针对整车模型将滑模控制与模糊控制结合,设计了一种模糊滑模控制器,并通过仿真验证所设计控制器在车身加速度、悬架动挠度和轮胎动位移方面的控制效果均优于传统滑模控制器。分析现有文献可知,将模糊控制与滑模控制相结合,在保证系统闭环稳定性的同时可以充分发挥模糊控制不依赖系统模型特点和滑模控制适用于非线性、时变系统的优势。
为此,本文提出一种考虑系统不确定性的车辆主动悬架自适应模糊滑模控制(Adaptive Fuzzy Sliding Mode Control, AFSMC)方法。首先,通过T-S模糊方法建立由于车辆悬挂和非悬挂质量变化、控制器输入不确定等因素引起的非线性主动悬架系统模型;接着设计积分滑模面函数,并采用并行分布补偿方法(Parallel Distribution Compensation, PDC)进行系统状态反馈控制;进而将滑模控制与自适应理论结合,引入自适应参数调节滑模趋近律的边界层来降低滑模抖振,保证系统状态轨迹在有限时间内到达滑模面;最后讨论了该控制方法应用于不同路面激励的悬架系统仿真结果。
在本文中,所使用标准符号如下:AT为矩阵A的转置;Rn为n维实数向量空间;P>0(≥0)为一个对称正定(半正定)矩阵;*为在对称块矩阵或复杂的矩阵表达式中,用*号来表示由矩阵对称性得到的矩阵块;diag{a1,…,an}为的块对角矩阵。sym(A)为A+AT;L2[0, ∞)表示在[0, ∞)是平方可积的。
1 系统建模及问题描述
为简化动力特性分析及控制器设计的复杂度,建立1/4汽车二自由度悬架动力学模型如图1所示[16-18]。其中,ms为悬挂部分质量;mu为非悬挂部分质量;zs,zu分别为悬挂质量和非悬挂质量的垂向位移;zr为随机路面输入;cs,ks分别为悬架结构阻尼和刚度;kt为轮胎刚度。
根据牛顿第二定律建立其动力学方程为
(1)
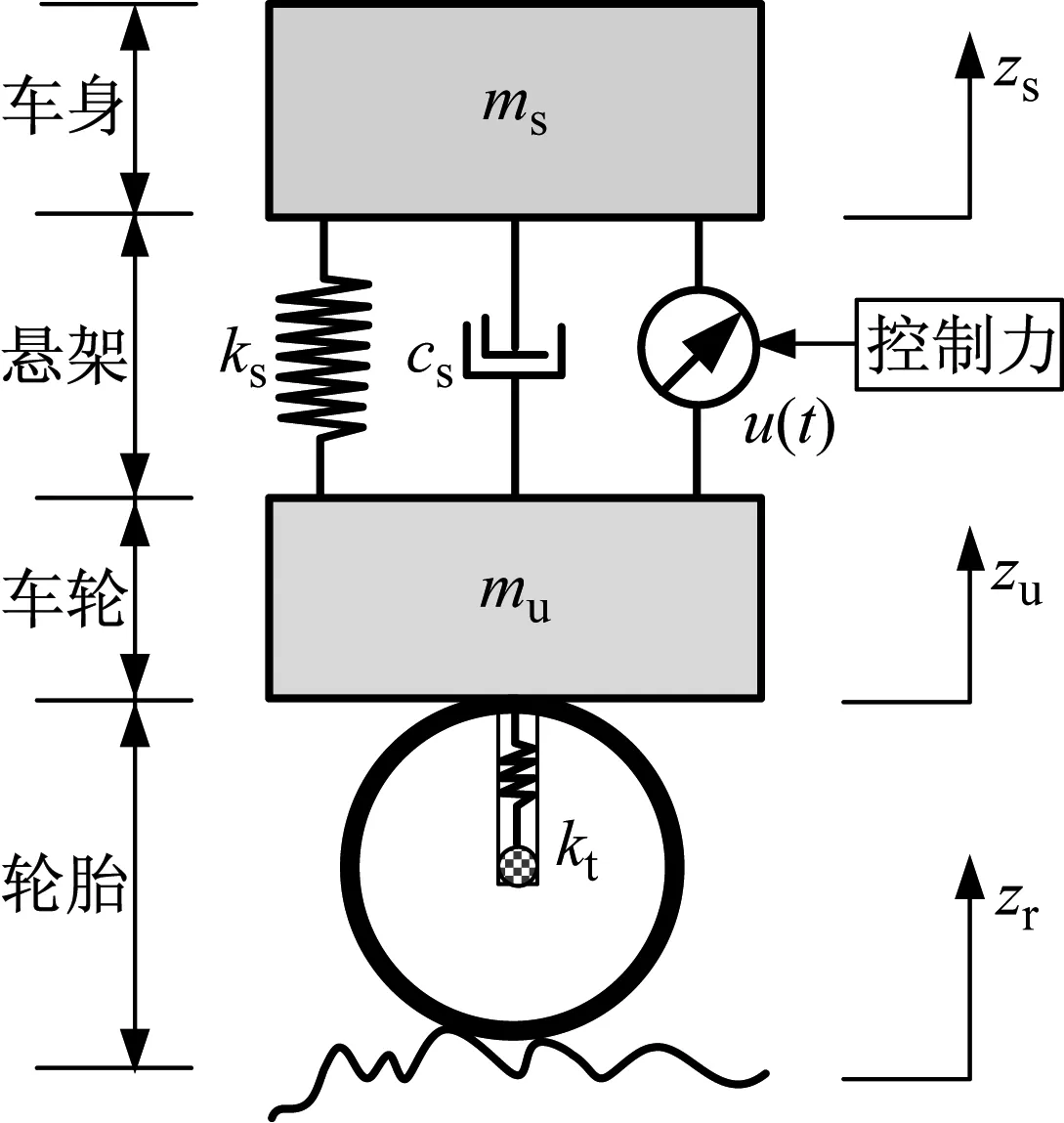
图1 二自由度1/4车辆主动悬架模型
(1) 考虑悬架系统机械结构的限制,悬架动挠度最大不能超过机械结构的限制值zmax,即
|zs(t)-zu(t)|≤zmax
(2)
(2) 为确保车轮与路面的不间断接触,轮胎动载荷必须小于轮胎静载荷,即
kt(zu(t)-zr(t))<(ms(t)+mu(t))g
(3)
式中:g为重力加速度且g=9.8(m/s2)。为满足式(1)和式(2)悬架性能约束,定义悬架控制输出为
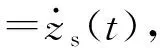
(4)
其中,
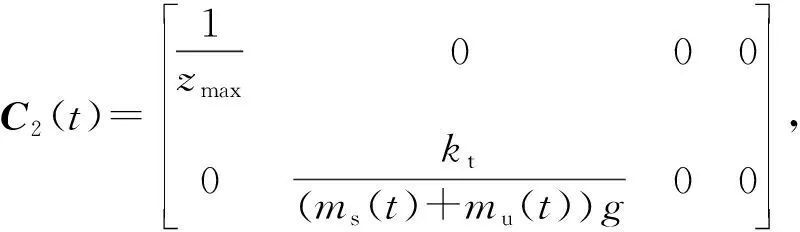
g(x(t))满足如下约束[19]
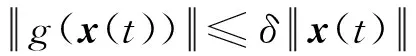
(5)
不同的车身载荷会使得车身质量ms(t)在一定范围内变化,同时作动器控制输入具有一定不确定性,因此,考虑系统不确定性的悬架运动方程包括悬挂质量ms(t)、非悬挂质量mu(t)以及作动器不确定控制输入。假定参数ms(t)和mu(t)变化范围为msmin≤ms(t) ≤msmax,mumin≤mu(t) ≤mumax,定义ξ1(t)=1/ms(t),ξ2(t)=1/mu(t), 参照文献[20]中非线性方法,可得1/ms(t)和1/mu(t)分别为
(6)
(7)
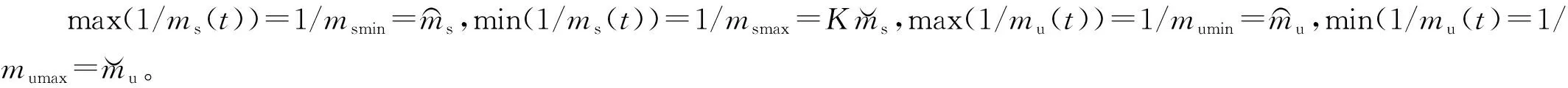
(8)
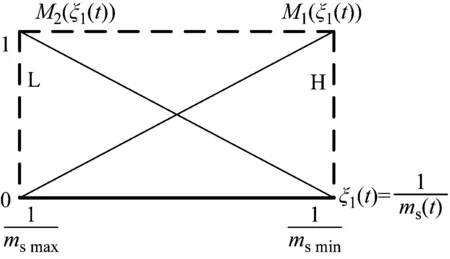
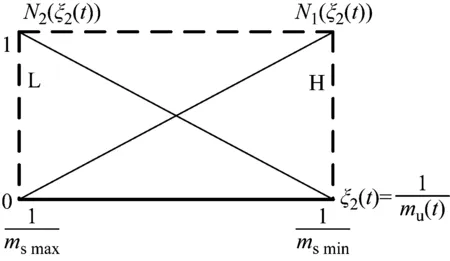
式中:M1(ξ1(t))+M2(ξ1(t))=1;N1(ξ2(t))+N2×(ξ2(t))=1,隶属函数M1(ξ1(t))和M2(ξ1(t))分别定义为“H(重)”和“L(轻)”,隶属函数N1(ξ2(t))和N2(ξ2(t))分别定义为“H(重)”和“L(轻)”,隶属度函数示意图如图2所示。
则具有不确定质量的悬架系统式(4)可用如下T-S模型描述
Model Rulei: IFξ1(t) isMrandξ2(t) isNj,
THEN
z1(t)=C1ix(t)+D1iu(t)
z2(t)=C2ix(t)
(9)
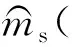
(a)
(b)
由此,根据上述模糊规则,考虑系统不确定性的车辆主动悬架系统可通过T-S模糊模型表示为
(10)
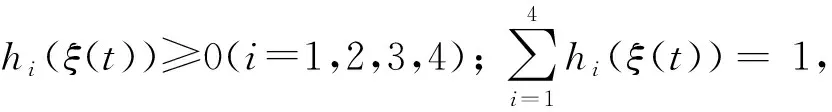
2 自适应滑模控制器设计
滑模动态的存在性、可达性以及滑模运动的稳定性是滑模控制的三个基本问题,针对1/4车辆主动悬架系统的模型不确定性,本文所提出自适应滑模控制器设计的主要问题是设计合适的滑模面函数和滑模控制律,根据式(2)式(3)的约束条件及滑模控制基本条件,要使本文所设计自适应滑模控制器u(t)达到滑模运动渐近稳定,则在零初始条件下应满足:① 闭环系统是内部稳定的;② 在能量有限外部扰动w(t)下,被控输出z能够满足约束,即
(11)

表1 权重系数及对应的模糊规则
|{z2(t)}r|≤1,r=1,2;t>0
(12)
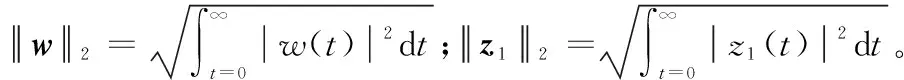
2.1 滑模切换面设计
设计滑模面函数为
(13)
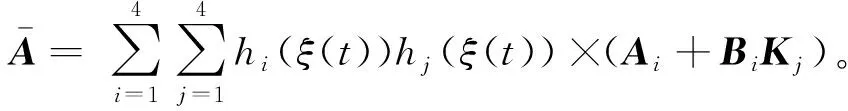
为了得到稳定T-S模糊模型,采用PDC方法进行系统状态反馈设计[21]。PDC方法的主要思想是将一个非线性系统动态划分成若干个线性子系统,针对每一个线性子系统,设计适当的局部线性控制器,最终通过权重系数产生由若干局部混合的模糊共混总控制器(补偿器)[22]。在PDC设计过程中,每条控制规则可设计为相应的T-S模糊模型规则,即所设计的模糊控制器与模糊模型共享相同模糊集,具体描述如下
Control Rulei: IFξ1(t) isMrandξ2(t) isNj(r=1,2;j=1,2)
THEN
u(t)=Kix(t) (i=1, 2, 3, 4)
(14)
则总的控制力可表示为
(15)
式中,Kj∈R1×4(j=1, 2, 3, 4)为状态反馈增益矩阵。
将式(15)代入式(10)得到
(16)
式(16)为模糊系统在滑模表面s(t)=0上的动力学方程,其滑模控制框图如图3所示。
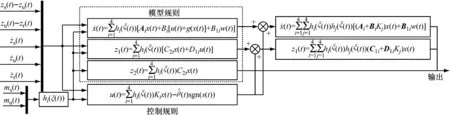
图3 基于T-S模糊模型的自适应滑模控制框图
2.2 滑模可达性分析
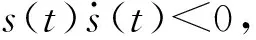
考虑在假设式(6)下的系统式(10),设计滑模控制律为
(17)
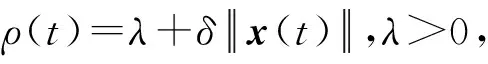
证明:定义Lyapunov函数为
将V1对时间求导,则有
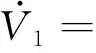
sgn(s(t))+g(x(t)))≤-ρ(t)|s(t)|+
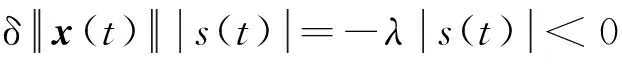
(18)
即系统式(10)的轨迹在有限时间将全部到达指定的滑模面s(t)=0上,证毕。
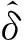
(19)
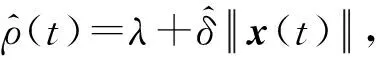
证明:定义Lyapunov函数为
将V2对时间求导可得
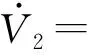
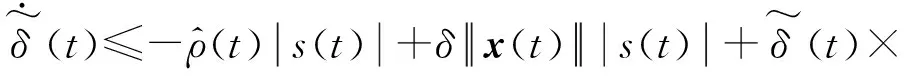
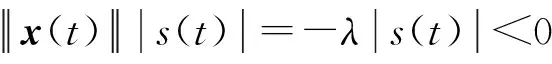
(20)
即在作动器不确定输入g(x(t))下,系统式(10)的轨迹可在有限时间内趋于指定的滑模面s(t)=0上,证毕。
2.3 系统稳定性分析
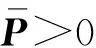
Ξii<0
(21)
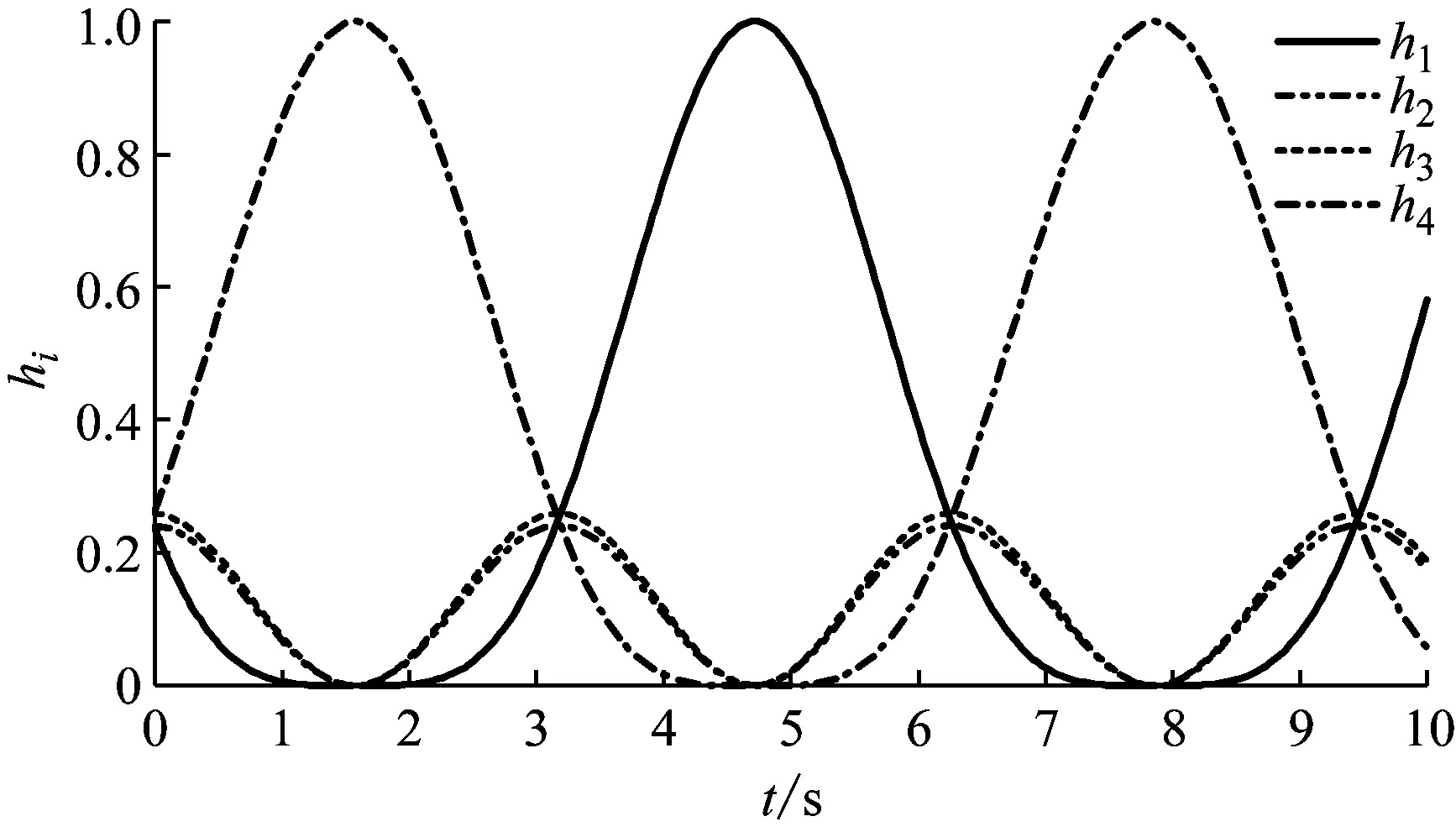
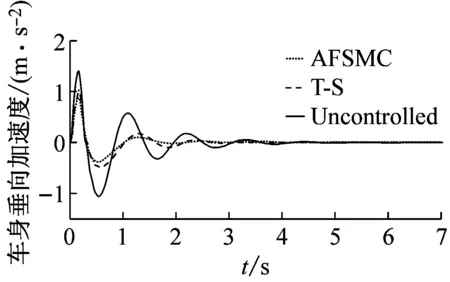
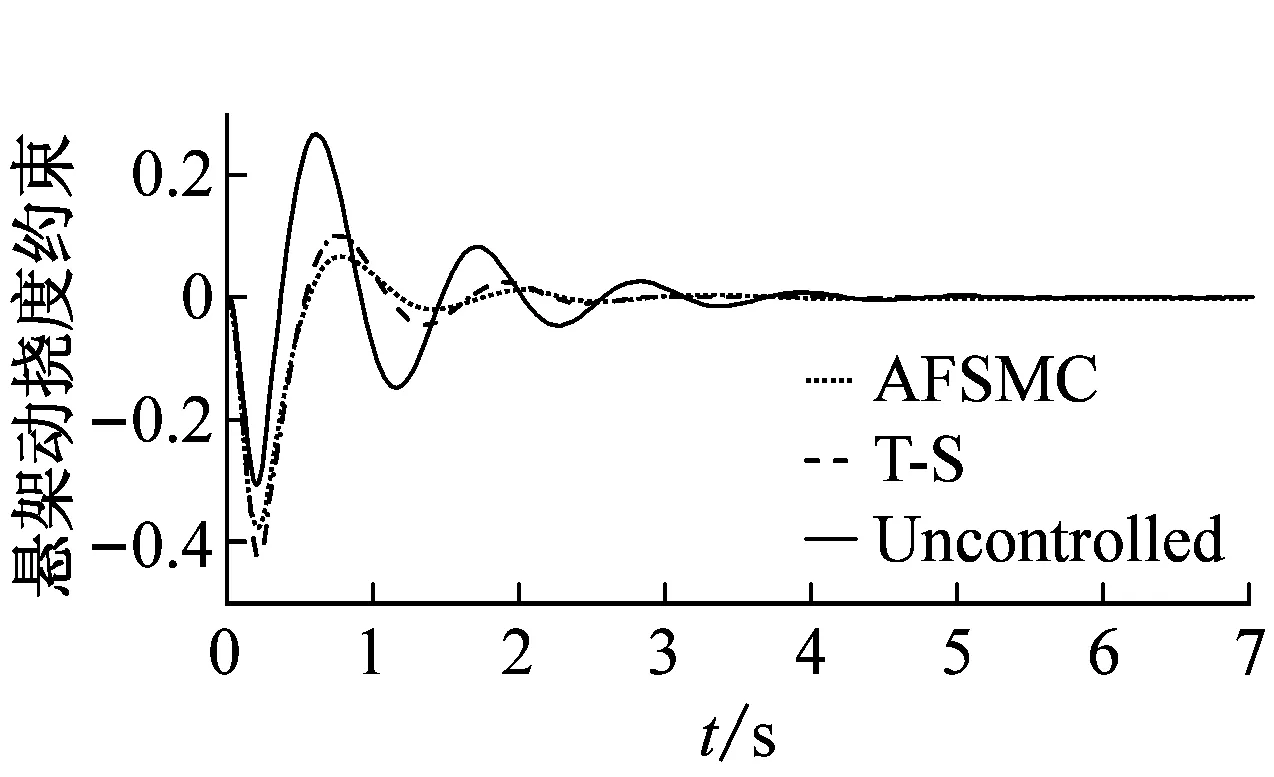
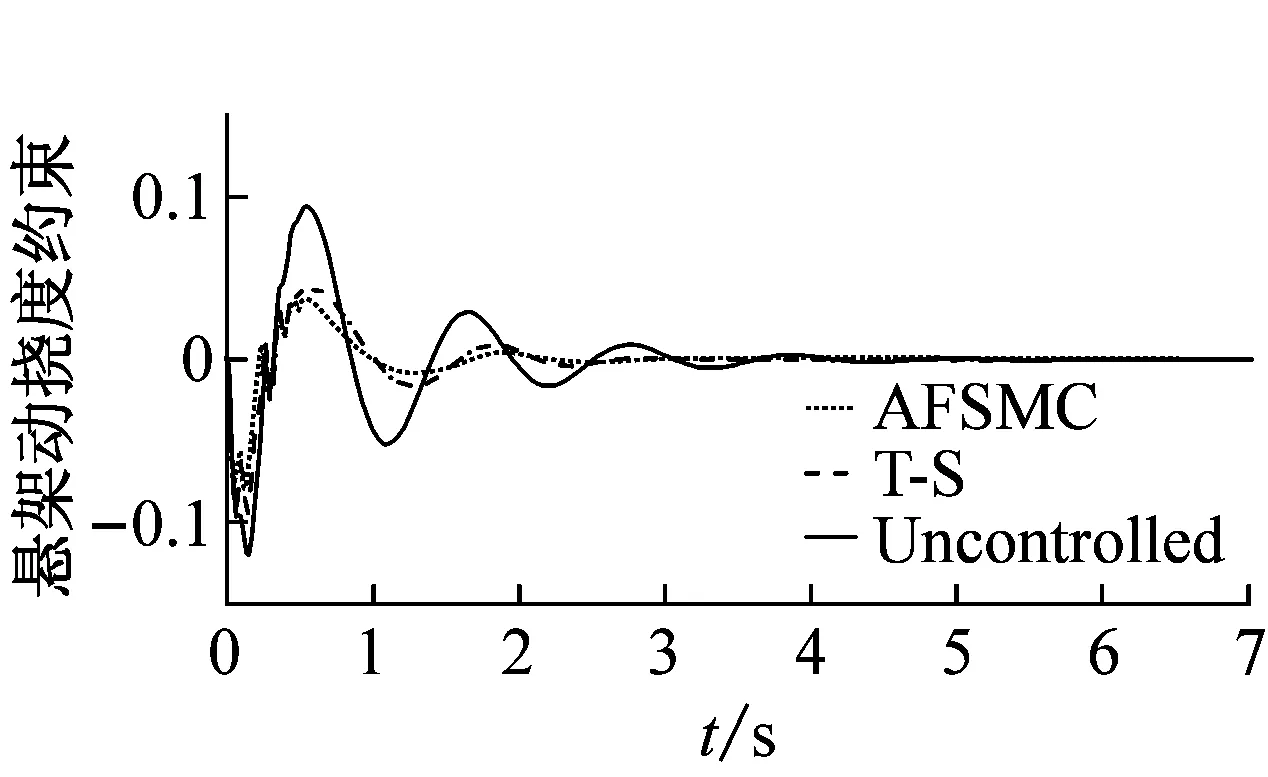
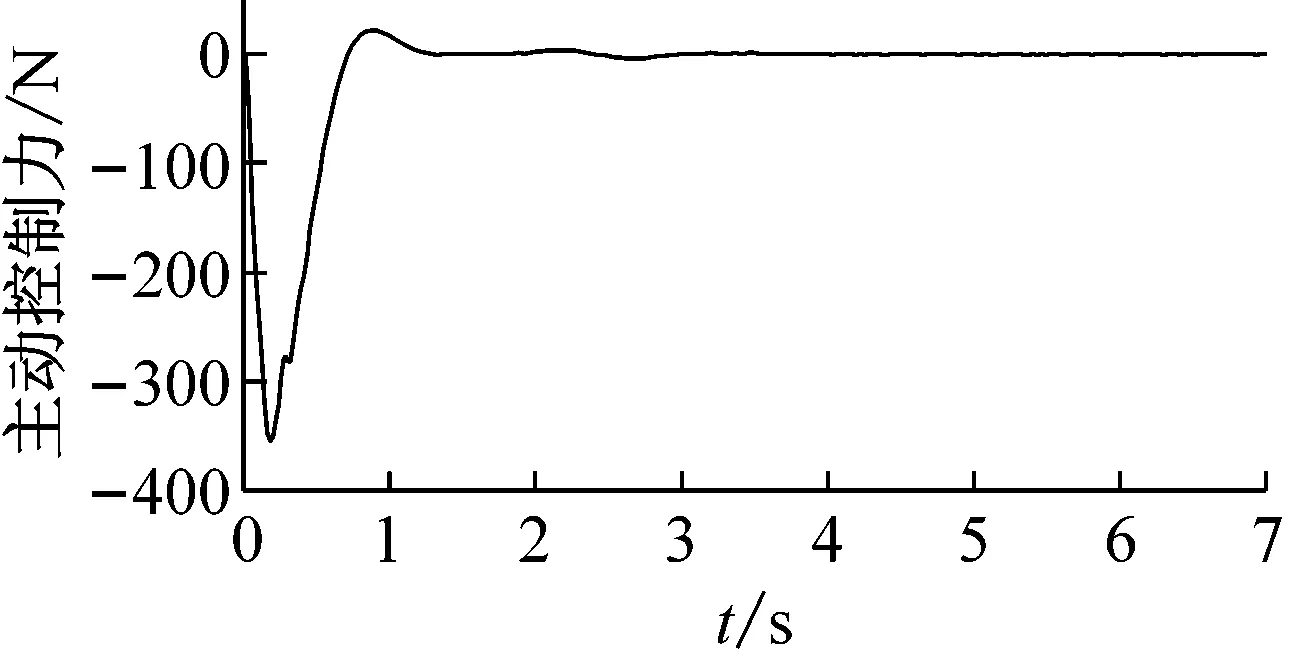
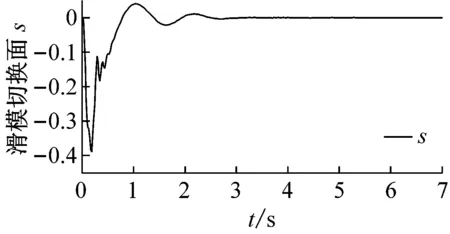
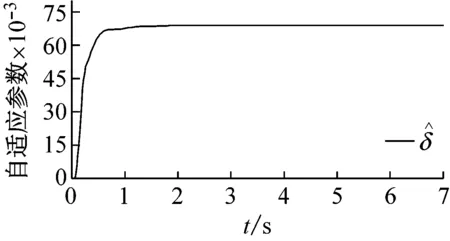
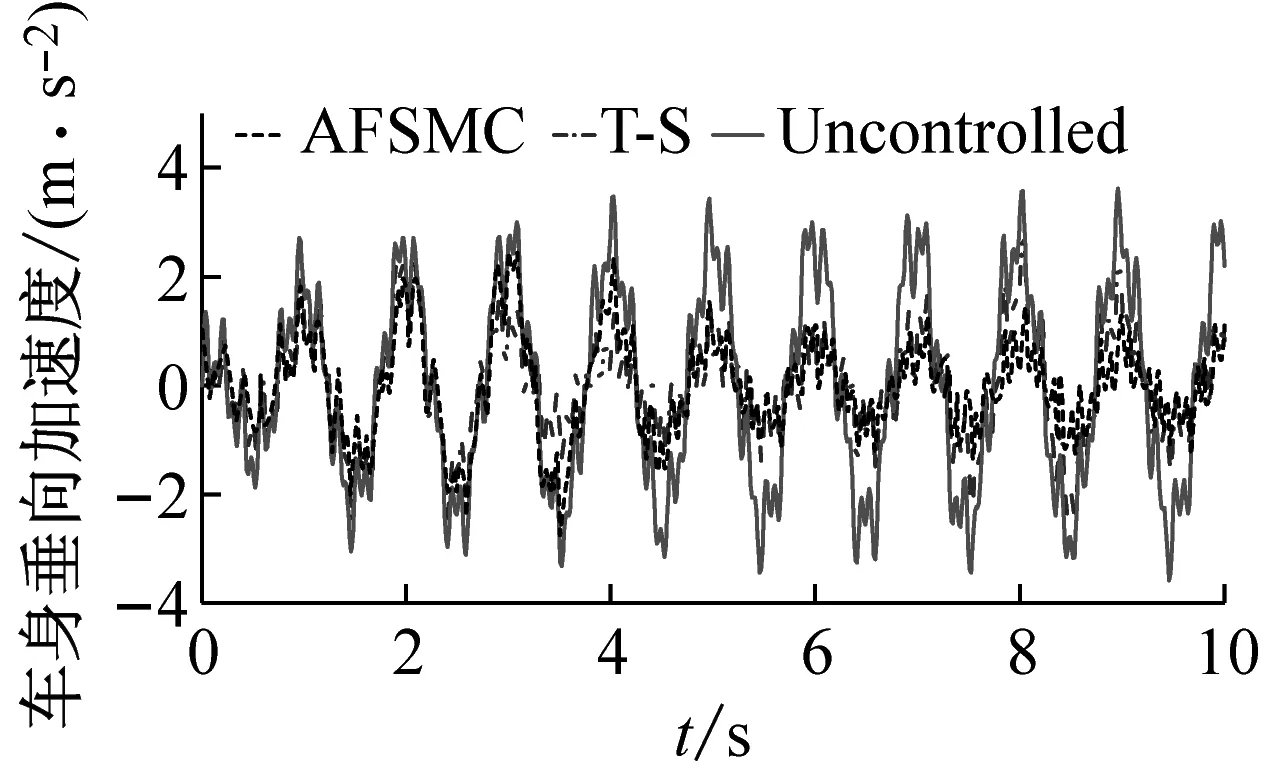
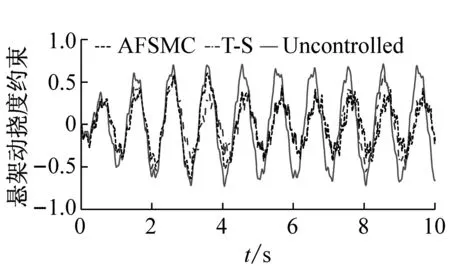
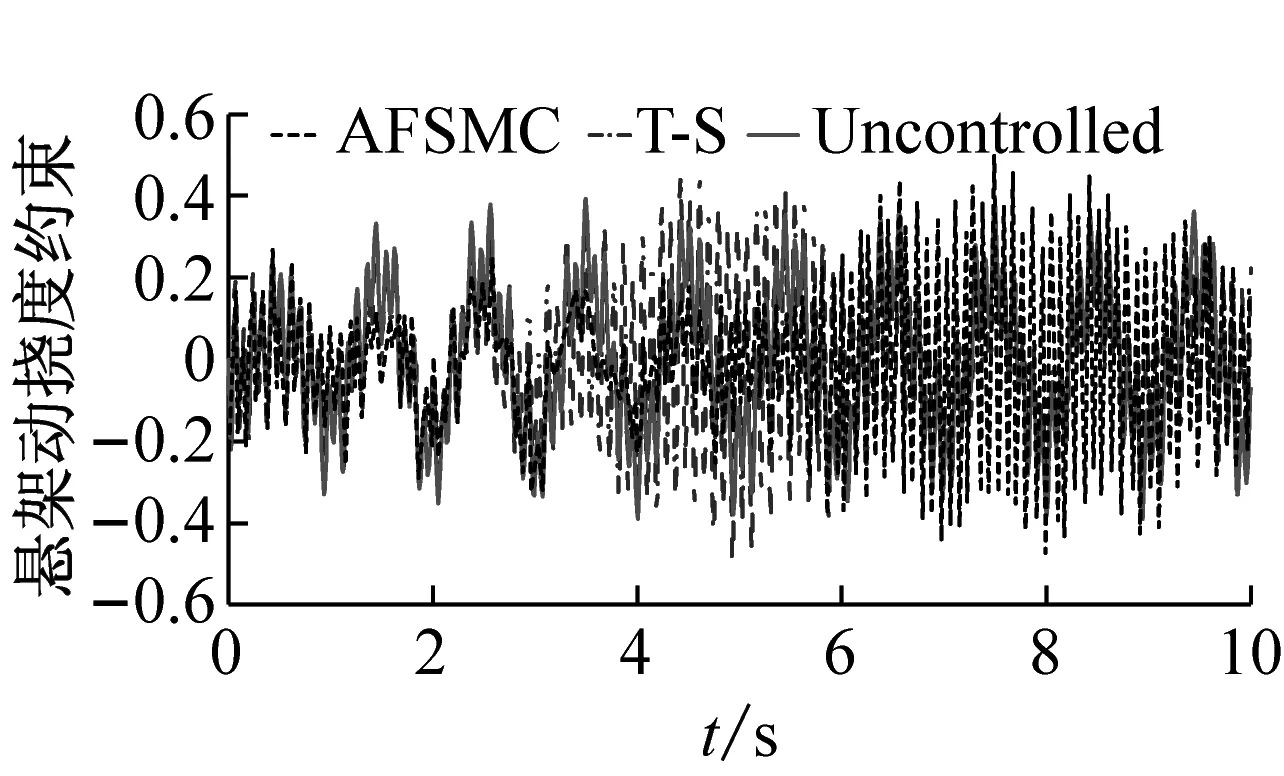
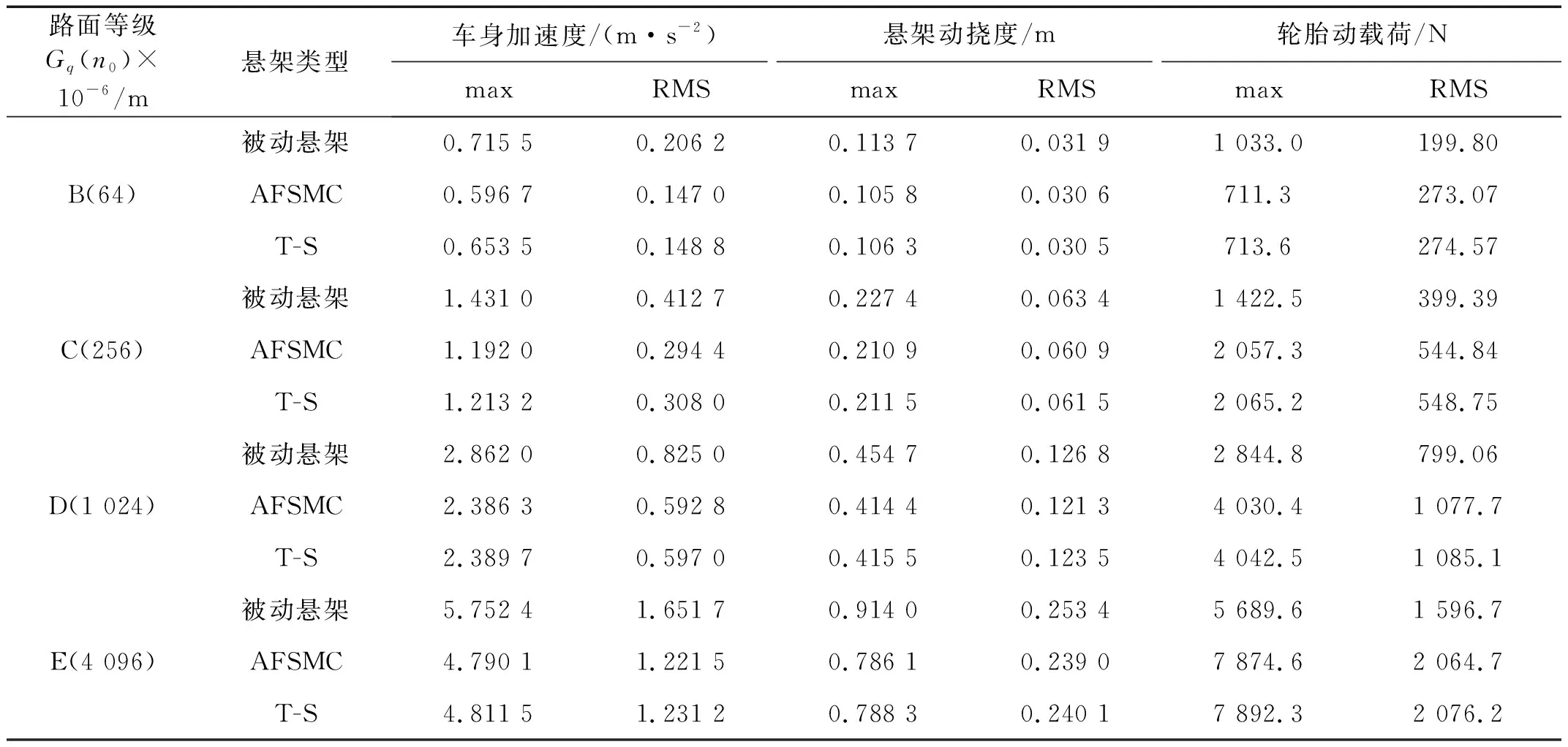
Ξij+Ξji<0,i (22) (23) 式中:i,j=1, 2, 3, 4且r=1, 2; 则控制系统式(10)存在一个状态反馈控制器式(17),使得:① 在没有扰动的情况下,闭环系统(16)是渐近稳定的;② 在零初始状态下,闭环系统式(16)在外界扰动能量小于wmax=(ρ-V(0))/γ2的情况下相应的闭环控制系统性能指标满足|Twz|∞<γ,且闭环系统输出约束式(12)在整个时间域内可以得到保证。 证明:定义如下Lyapunov函数 V=xTPx (24) 且PT=P>0,则 (25) 其中, (26) 对于任意能量有限的外界扰动w={w(t)}∈L2[0,∞),利用Schur补性质可将式(27)等价转化为 (27) 当外界扰动w(t) = 0时,则式(16)所描述系统的Lyapunov函数导数可表示为 (28) 综上可知,该控制系统在任意能量有限的外界扰动下是渐近稳定的。接下来证明零初始条件下,闭环系统输出式(11)式(12)的充分必要条件。 (29) 根据Lyapunov函数V(t)的定义可得xT(t)Px(t)<ρ且ρ=γ2wmax+V(0),为了满足式(12)的约束条件,则应保证 式中:r=1,2;θmax(·)表示·最大特征值。 (30) 根据Schur补性质可将矩阵不等式的可行性问题等价转化为 (31) 为验证本文所提出控制策略的有效性和适用性,假定车辆载荷在行驶过程中发生最剧烈的变化(即悬挂质量变化函数式为ms(t)=432+20sin(t) (kg),非悬挂质量变化函数式为mu(t)=45+0.45sin(t) (kg),基于Matlab/Simulink建立1/4车辆主动悬架系统控制仿真模型。根据表1中模糊规则,可得该主动悬架线性子系统权重系数hi(ξ(t))如图4所示。本文研究所 图4 权重系数hi 采用的某型号轿车的悬架参数见表2。 表2 四分之一车辆悬架参数 为保证所设计的自适应模糊滑模控制器在指定滑模面是渐近稳定的,同时其状态轨迹可在有限时间内到达滑模面并满足悬架系统硬约束条件式(11)、式(12),选择 G=[0 0 1 1] (32) K1=103×[1.960 6 -1.360 0 -1.975 9 1.013 6] K2=103×[1.949 2 -1.351 5 -1.961 3 1.040 2] K3=103×[1.959 2 -1.359 0 -1.935 2 0.437 1] K4=103×[1.965 3 -1.363 5 -1.942 7 0.508 5] (33) P= (34) 凸块路面输入可看作来自路面的突变或冲击,它通常是短时间、高强度的离散事件,例如横过道路的水沟、减速带、与公路交叉的铁轨等,这种振动路面输入也是验证悬架系统设计性能经常采取的扰动输入形式,根据国际标准ISO2361,其数学描述可写为 (35) 式中:A和L分别为凸块输入的高度和长度,假定其值分别为A=50 (mm),L=5 (m),并且车辆以36 (km/h)车速匀速行驶。图5~图7为被动悬架、T-S控制和自适应模糊滑模被控悬架的车身加速度z1响应曲线、悬架动挠度输出约束曲线和轮胎动载荷输出约束曲线。 从图5可知,相比于被动悬架系统,自适应模糊滑模控制的车身垂向加速度具有更小的峰值,能够快速抑制车身振动;从图6、图7可以看出,悬架动挠度远小于zmax,约束式(2)得到保证,可以有效地减少车轮的冲击而使悬架与限位块碰撞的次数,降低悬架被“击穿”的概率,改善汽车的操作稳定性;相较于T-S模糊控制,自适应滑模控制具有更低的车身加速度峰值,更短的稳定时间,对提升乘坐舒适性有较大帮助;此外,自适应模糊滑模控制悬架轮胎动态负载与静轮胎载荷最大比值远小于1,悬架具有可靠地承载能力,能够确保汽车行驶过程中车轮不间断的接地性,具有更好的抓地能力。 图5 车身加速度响应曲线 图6 悬架动挠度输出约束 图7 轮胎动载荷输出约束 图8为自适应模糊滑模控制的主动控制力变化曲线,当车辆受到瞬态冲击时,主动悬架可做出快速响应;同时,从图9和图10可以看出,控制系统状态轨迹能在有限时间内进入到滑模面,保证滑模面为滑动模态区,滑模运动渐近稳定且具有良好的动态品质。 图8 主动控制力u 图9 滑模面s 图10 自适应参数 为验证自适应模糊滑模控制器在车体共振频率(1 Hz)输入扰动下的控制效果,以车体共振频率与高频干扰叠加的粗糙路面作为路面输入,粗糙路面实际上是具有一定波长和微小沟槽的搓板路,其数学描述如式(36)所示[23] zr=0.025 4sin(2πt)+0.005sin(10.5πt)+ 0.001sin(21.5πt) (36) 在粗糙路面输入扰动下,图11为被动悬架、T-S控制和自适应模糊滑模被控悬架的车身加速度z1响应曲线,图12和图13分别为悬架动挠度和轮胎动载荷的输出约束曲线。 从图11可知,在整个粗糙路面上自适应模糊滑模控制较被动悬架的车身垂向加速度降低了46.6%,很好改善了汽车行驶平顺性;从图12可以看出,悬架动挠度满足机械结构限制约束;从图13可以看出,由于三种性能指标之间相互矛盾,自适应模糊滑模控制轮胎动载荷峰值较被动悬架有所增大,但轮胎动态载荷与静轮胎载荷比值小于1,依然能够确保汽车具有一定的安全行驶性能;相较于T-S模糊控制,自适应滑模控制策略三种性能指标均有较小幅度的改善,具有更好的悬架动态性能。 为进一步评估自适应模糊滑模控制器性能,假定路面输入为随机路面,随机路面是指持续长时间的小不平整路面,路况相对较好,如一般的沥青路面、砂石路面等。其输入可用下式来表示[24] 图11 车身加速度响应曲线 图12 悬架动挠度输出约束 图13 轮胎动载荷输出约束 (37) 式中:n0为空间频率(n0= 0.1(1/m));Gq(n0)为路面不平度系数(10-6(m3));u为车辆行驶速度,取u=20(m/s);fc为路面时间截止频率(取值fc=0.01(Hz));W(t)表示均值为0,强度为1的均匀分布白噪声。 车身加速度的均方根值(RMS)与汽车乘坐舒适性是严格相关的,其值常被看为传递到车体上的加速度的量。车身加速度、悬架动挠度和轮胎动载荷的均方根值通常用来评估所提出的控制设计方法的有效性。在本文中,选择时间T= 100 s来计算的车身加速度、悬架动挠度和轮胎动载荷在不同路面平整度系数下B级路面(Gq(n0)=64×10-6(m3))、C级路面(Gq(n0)=256×10-6(m3))、D级路面(Gq(n0)=1 024×10-6(m3))、E级路面(Gq(n0)=4 096×10-6(m3))的均方根值和最大值(max),计算结果见表3。其中,变量x(t)的均方根值的计算公式为[25] 表3 悬架系统性能值 (38) 观察表3可知,在不同等级的随机路面下,与被动悬架相比,自适应模糊滑模控制策略的车身垂向加速度均方根值降低了16.7%;悬架动挠度均方根值随路面等级变差而改善幅度增大,有效降低了汽车行进间的路面激励对车身产生的冲击,减少了车轮的冲击而使悬架与限位块碰撞的次数,降低悬架被“击穿”的概率,很好的改善了汽车行驶平顺性和操作稳定性,由于三种性能指标之间相互矛盾,轮胎动载荷峰值较被动悬架有所增大。与T-S模糊控制相比,自适应模糊滑模控制能够很好地抑制车身加速度的幅值,减小了车轮的动载荷和车轮跳动量,改善了车辆的乘坐舒适性和操作稳定性,车辆悬架综合性能得到了较好的提高。 (1) 对于主动悬架系统,车辆悬架系统的性能会受到车辆有效载荷的影响。为了解决车辆主动悬架因系统质量参数不确定性所引起的控制稳定问题,建立了基于T-S模糊方法的悬架系统非线性控制模型,通过T-S模糊模型来描述由于悬挂和非悬挂质量变化、控制器输入不确定等因素所引起的不确定性,提出一种自适应模糊滑模控制策略,并利用Lyapunov理论推证了自适应滑模控制系统的稳定性和滑模面的可达性。 (2) 通过在三种不同路面激励下的仿真实验发现,相比于被动悬架和模糊控制,在凸块路面扰动下,自适应滑模控制具有更低的车身加速度峰值,更短的稳定时间,对提升乘坐舒适性有较大帮助;在车体共振频率(1 Hz)与高频干扰叠加的粗糙路面和随机路面扰动下,车辆悬架综合性能得到了较好的提高。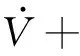
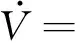
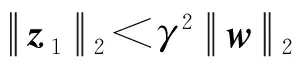
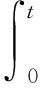
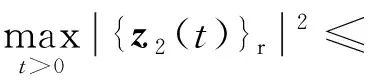
3 仿真分析
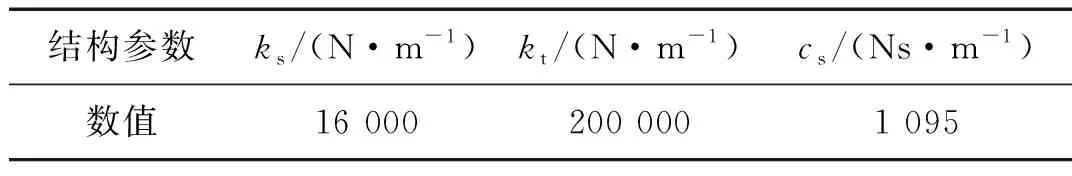
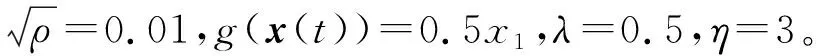

3.1 凸块路面响应
3.2 粗糙路面响应
3.3 随机路面响应
4 结 论
