基于实测相电流的永磁同步电机转矩波动阶次来源分析及幅值预测

毛 钰, 左曙光, 邓文哲, 曹佳楠

(同济大学 新能源汽车工程中心， 上海 201804)

轮毂电机驱动电动汽车因其结构布置简化，驱动效率高，底盘动力学控制方便等优势成为电动汽车方向的重点研究对象之一[1-3]。永磁同步电机具有功率转矩密度高、效率高等优点，因此成为轮毂电机的最优选择[4]。由于转子磁场非正弦分布、定子开槽及电流谐波等因素影响，永磁同步电机输出转矩中不可避免地存在波动[5]，驱动电机转矩波动作用于传动系统将会给电动汽车带来振动噪声问题[6-7]，如引起动力总成的电磁振动等[8]。因此关于轮毂电机转矩波动的研究引起了学者广泛的关注。

在转矩波动解析建模方面，Zarko等[9]通过线圈磁场叠加求解电枢反应磁场并在气隙磁场精确求解的基础上解析计算了电磁转矩，但模型复杂不便于分析转矩波动阶次特征及来源。左曙光等[10]从电枢反应磁场和永磁体磁场相互作用的角度建立了电动车用永磁同步电机转矩计算和波动特性分析的解析模型，并分析了转矩波动阶次特征及其来源，但由于气隙磁场分布特征难以解析求解并且不易通过试验获得，模型中分布参数无法确定，该模型不适用于转矩波动定量计算。李景灿等[11]考虑饱和以及转子磁场谐波的影响建立了永磁同步电机非线性dq轴模型，采用三相电机一般化dq轴建模方法能够有效地通过有限元或试验识别模型参数，为转矩波动的准确计算及分析提供了基础，但论文没有考虑变频器供电下三相电流谐波的影响。马琮淦等[12]在此基础上建立了考虑转子磁场谐波、定子开槽和时间谐波电流等因素的统一转矩波动解析模型，完善了转矩波动的解析建模，但该模型并未明确永磁体磁链等参数的获取方法，而且关于时间谐波电流的相序关系也没有根据实际情况进行区分。在转矩波动分析方面，文献大多侧重于针对频率和阶次特性从理论角度揭示转矩阶次波动现象并解释其阶次来源[13-15]，并未定量关注各阶次幅值大小进而确定转矩波动主要贡献因素及其影响机理。

针对上述情况，本文基于实测空载反电动势和负载相电流分析了轮毂永磁同步电机转矩波动阶次特征及其来源，并对各阶次幅值进行了预测，确定了该轮毂电机转矩波动主要贡献因素及其影响机理，从而为转矩波动的有效抑制和电动轮振动特性的改善提供了参考。论文首先介绍了轮毂电机台架试验设置及测试工况，然后分别基于实测的电机空载反电动势和负载相电流确定了转子磁通系数和电流谐波信息，最后考虑转子磁通和相电流谐波解析推导了电磁转矩表达式，分析了转矩波动阶次来源并根据电流谐波幅值和相位规律预测了各阶次幅值大小，进而确定了各因素对转矩波动的贡献并通过实测的振动加速度信号间接验证了转矩波动阶次分析及幅值预测的准确性。

1 轮毂电机台架试验设置

为真实反映轮毂电机工作及输出特性，本文基于某分布式驱动电动汽车前轮驱动系统进行试验，该前驱系统采用轮毂电机驱动，包括轮毂电机、轮胎/车轮和双横臂悬架，并配合前期开发的可调试验台架[16]以及转鼓系统模拟实车运行工况下轮毂电机的工作情况。试验布置如图1所示，轮毂电机为轴向磁通永磁同步电机，电机控制器为永磁同步电机通用控制器，控制算法采用id=0的矢量控制，由上位机通过串口通信输入控制指令，电机及控制器相关参数如表1所示。

图1 轮毂电机台架试验布置

物理量/单位数值极对数15槽数27额定功率/kW2.8直流母线电压/V80开关频率/Hz10 000

试验中测量的信号包括电机相电压、相电流及轮心处振动加速度信号。由于轮毂电机安装条件的限制，无法布置转矩传感器，因此本文通过轮心处振动加速度信号间接反映轮毂电机转矩波动。

试验测试工况主要包括两类：① 空载倒拖试验，由转鼓拖动电机到某一恒定的转速，此时电机三相开路，测量电机空载相电压；② 负载驱动试验，控制器给电机供电并控制电机输出转矩，驱动转鼓转速稳定在固定值，转鼓根据该转速下车辆行驶阻力对电机施加某一恒定负载，测量电机相电流和轮心振动信号。通过空载倒拖试验测得的反电动势能够反映转子磁场分布情况，进而从结构的角度分析转子磁通谐波对转矩波动的影响。通过负载驱动试验能够反映供电电流特征，进而从控制器的角度分析电流谐波对转矩波动的影响。

2 轮毂电机转子磁通谐波分析

永磁同步电机理想模型假定转子磁场在气隙中呈现正弦分布，但实际上由于永磁体磁极在制造及工艺上的限制，气隙中转子磁场在空间并不是理想正弦分布而是包含(2n-1)次谐波，进而导致三相绕组中转子磁通随转子位置非正弦变化，可表示为

(1)

式中：ψma为A相磁链；ψ2i-1为空间(2i-1)p阶磁场产生的定子磁链幅值；p为电机极对数；θ为转子d轴超前A相轴线的空间角度。式(1)对时间求导可确定相感应电动势为

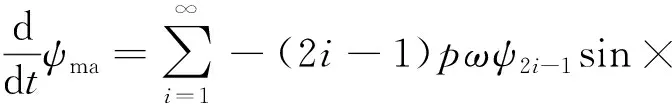
[(2i-1)pθ]

(2)

式中：Vma为A相反电动势；ω=dθ/dt为转子旋转角速度。

图2为空载倒拖工况下电机转速为200 r/min时A相反电动势，图3为经过快速傅里叶变换得到的空载反电动势频谱图，与理论分析一致，感应电动势中除基波外还存在奇数阶谐波，其幅值随谐波阶数增加而降低，其中3及3的倍数次谐波为零相序，通过坐标变换到dq轴时将不复存在，对转矩输出不会产生影响，因此反电动势及磁链谐波中5次和7次谐波影响最为显著。由实测反电动势谐波大小根据式(2)确定转子磁通主要谐波阶次的幅值如表2所示。

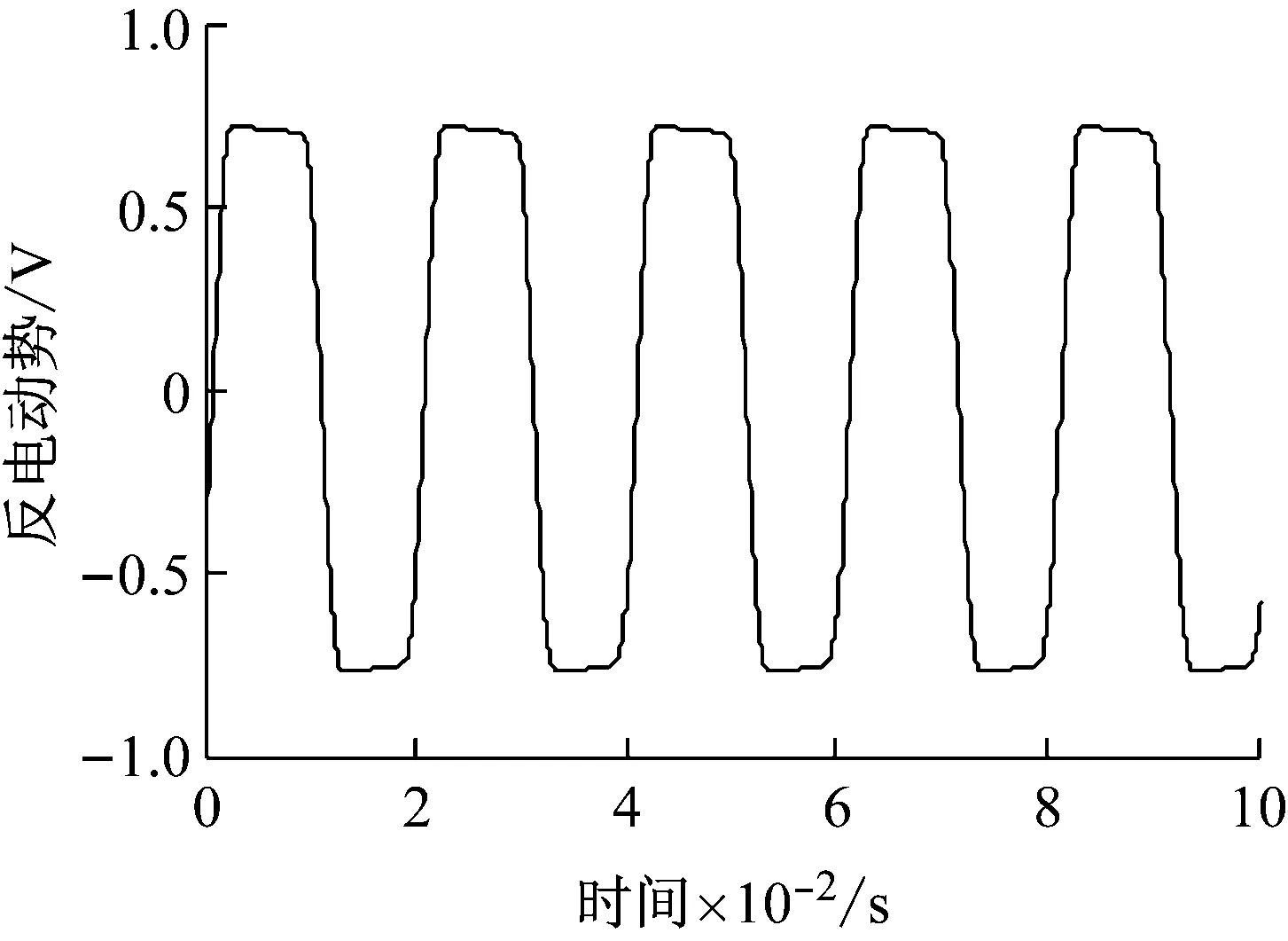
图2 200 r/min时电机A相空载反电动势

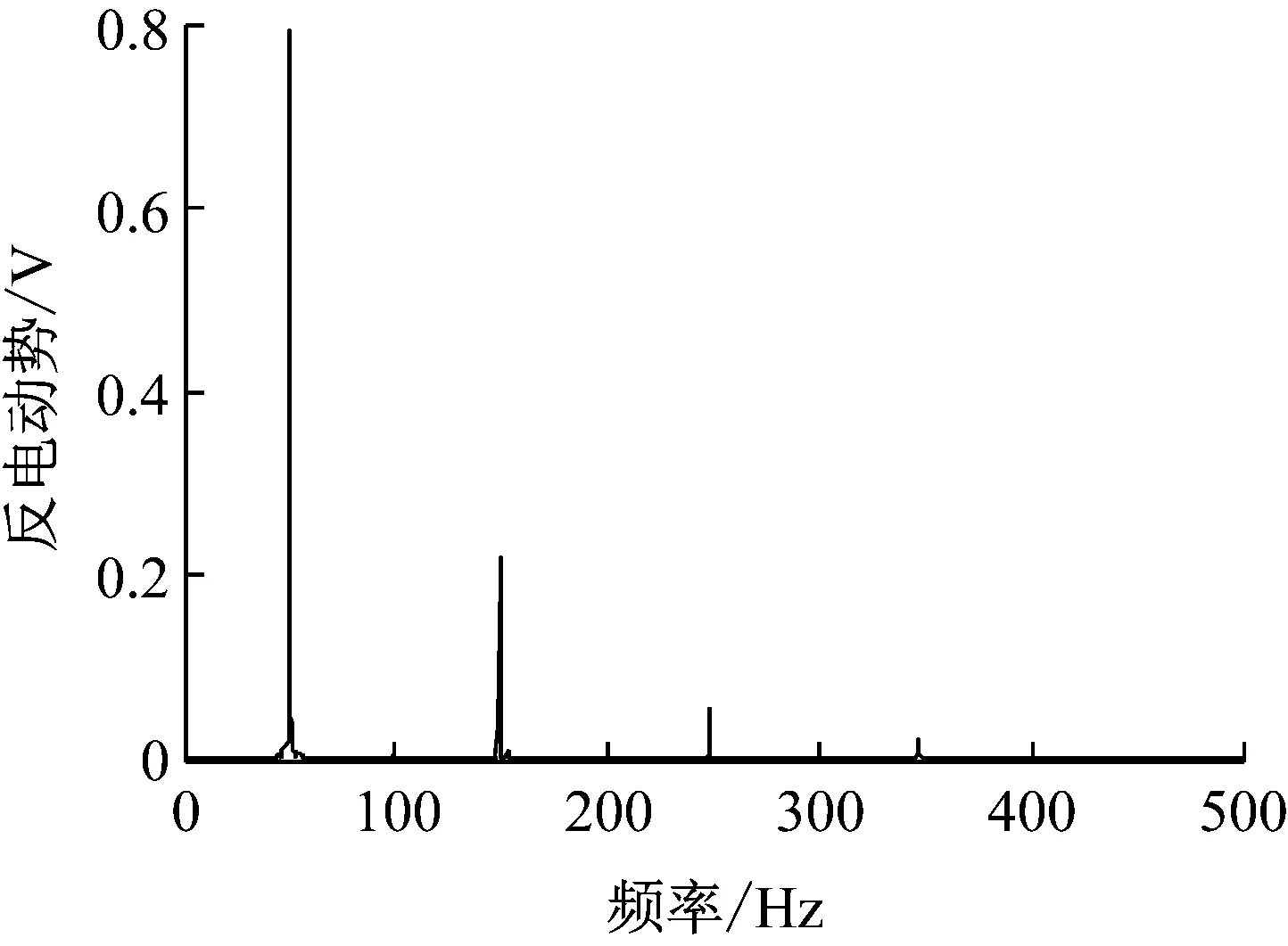
图3 200 r/min时电机A相空载反电动势频谱

参数数值磁通基波ψma/Wb0.038 145次磁通谐波ψ5/Wb1.065×10-37次磁通谐波ψ7/Wb2.966×10-4

3 轮毂电机定子相电流谐波分析

轮毂永磁同步电机采用控制器进行变频调速，由于空间矢量脉宽调制算法、转子位置及电流传感器误差和逆变器死区时间等的影响，变频器供电使得三相电流不是简单的正弦波形，而存在大量的时间谐波。因此电机三相电流可表示为

(3)

式中：iA，iB，iC分别为A，B，C三相电流；i1为基波电流幅值；φ1为基波电流相位；ih为h次谐波电流幅值；φh为h次谐波相位；sh=±1，当sh=1时，定子三相电流按ABC顺序依次滞后120°，h次谐波电流为顺相序电流；当sh=-1时，定子三相电流按ACB顺序依次滞后120°，h次谐波电流为逆相序电流。

图4为负载驱动工况下电机从10～100 r/min匀加速时A相电流时频图(由时域信号经短时傅里叶变换得到)，相电流表现出阶次特征，除幅值最大的p阶电流基波外，还存在0.6p，0.8p，1.2p和1.4p阶电流谐波。进行阶次切片得到电流基波及上述四阶电流谐波随转速变化规律如图5所示，由图可知，随着谐波阶次远离基波其幅值逐渐降低，即0.8p和1.2p阶谐波幅值明显大于0.6p和1.4p阶谐波幅值；另外在负载恒定的情况下电流谐波大小随转速变化不大，因此不失一般性，基于电机恒定转速运行工况下的实测相电流进行具体分析。

图4 电机加速工况下A相电流时频图

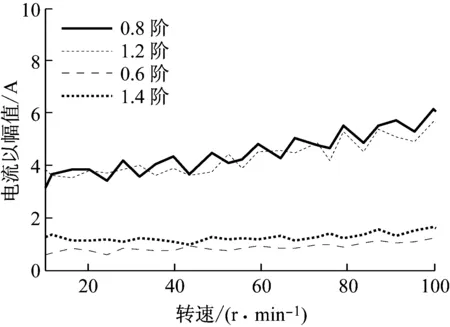
图5 各阶电流谐波随转速变化

图6为负载驱动工况下电机100 r/min时A相电流时间历程，为便于分析，选取电流基波相位为π/2的时刻为零时刻，由于该电机采用id=0的控制策略，此时θ=0 rad。由图可知，相电流存在一定的畸变，通过傅里叶变换得到其频谱曲线如图7所示，电流基波频率为25 Hz (100/60p)，主要谐波频率为15 Hz (100/60 0.6p)、20 Hz (100/60 0.8p)、30 Hz (100/60 1.2p)和35 Hz (100/60 1.4p)，以基波为中心谐波幅值呈现阶梯下降。同样地，对B和C相电流进行分析得到电机在100 r/min驱动负载工况下三相电流基波及主要谐波信息如表3所示，电机基波和谐波均为对称三相交流信号，即三相幅值相等，相位相差2π/3，而且谐波与基波一致均表现为顺相序，后续将基于各阶相电流幅值和相位信息预测和解释转矩波动规律。

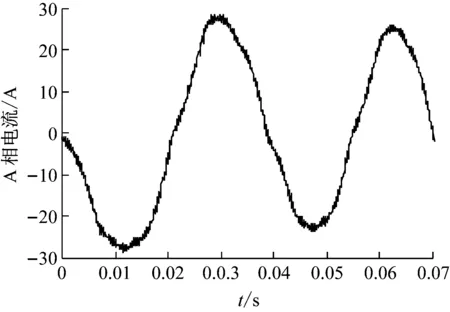
图6 电机100 r/min时A相电流

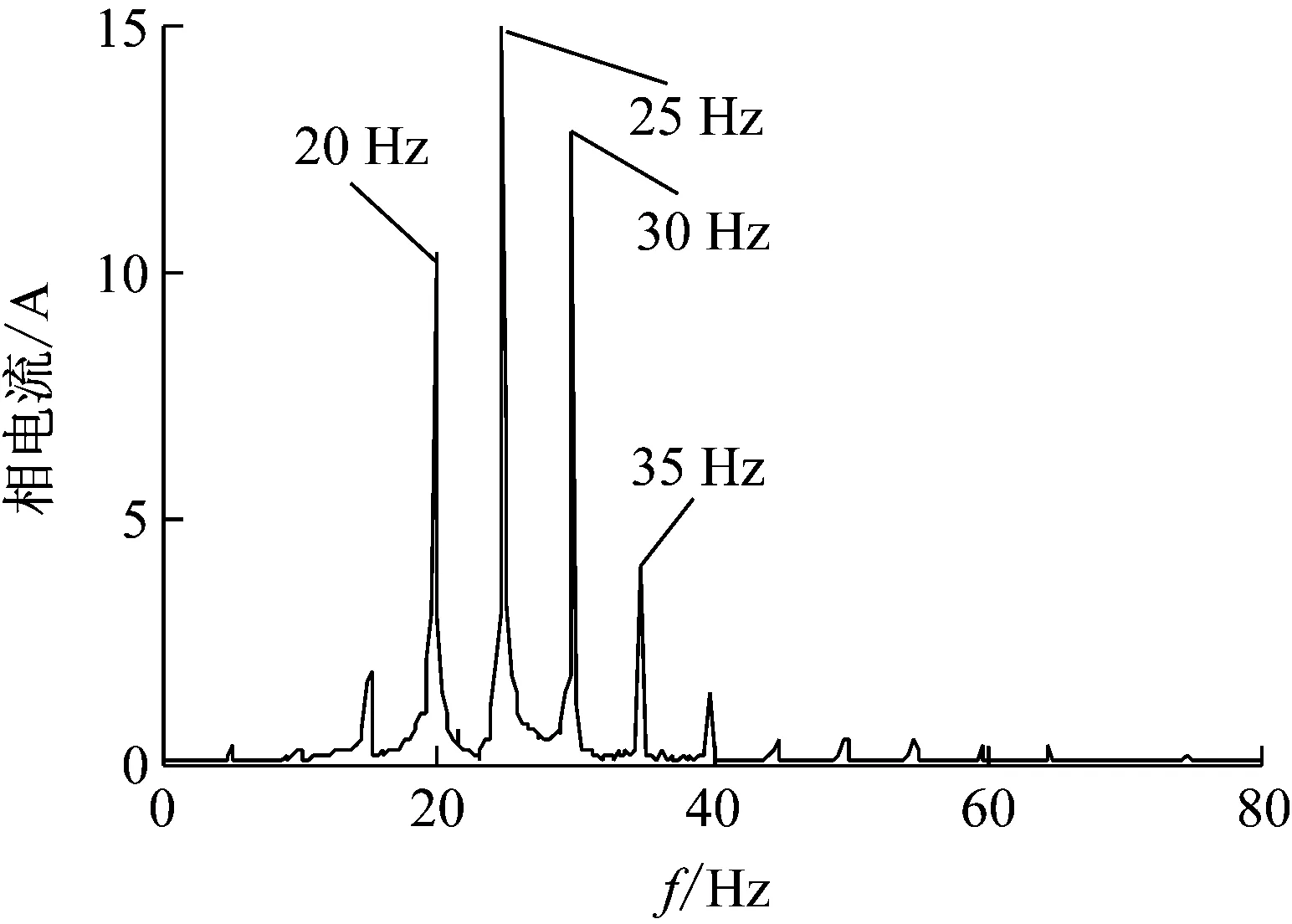
图7 电机100 r/min时A相电流频谱

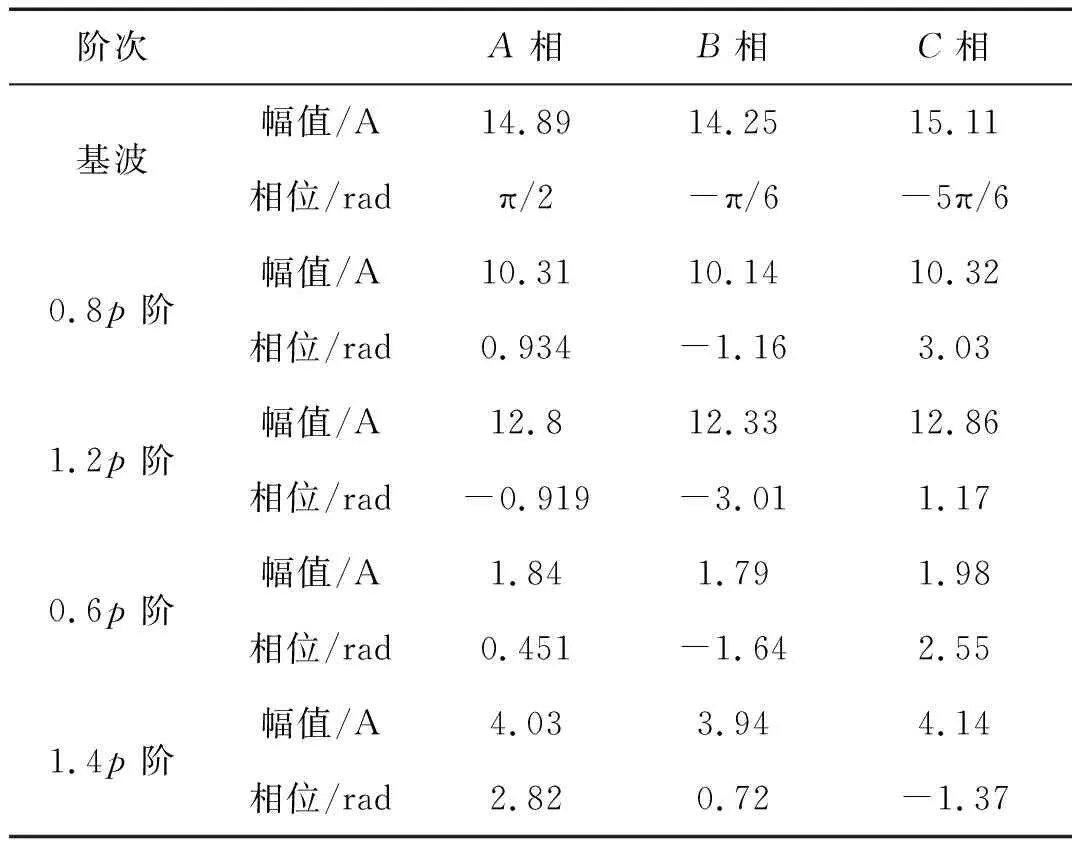
阶次A相B相C相基波0.8p阶1.2p阶0.6p阶1.4p阶幅值/A14.8914.2515.11相位/radπ/2-π/6-5π/6幅值/A10.3110.1410.32相位/rad0.934-1.163.03幅值/A12.812.3312.86相位/rad-0.919-3.011.17幅值/A1.841.791.98相位/rad0.451-1.642.55幅值/A4.033.944.14相位/rad2.820.72-1.37

4 转矩波动分析

4.1 考虑转子磁通谐波和电流谐波的转矩波动解析推导

由于转子磁场非正弦分布、定子开槽及电流谐波等因素影响，永磁同步电机输出转矩中不可避免地存在波动，本文研究的轴向永磁同步电机为30p/27s，由定子开槽引起的齿槽转矩对应阶次较高(转频270倍)而且幅值较小，对电动轮系统振动影响微弱，因此在对转矩波动进行分析时忽略定子开槽的影响。考虑转子磁场非正弦分布可得到dq轴坐标下电磁转矩解析表达式为

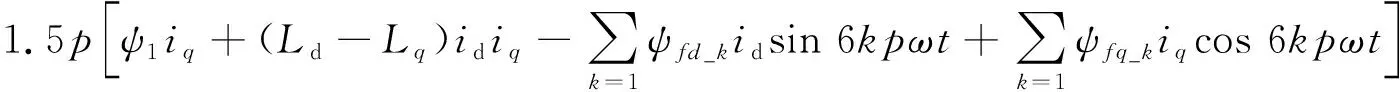
(4)

其中,

ψfd_k=(6k-1)ψ6k-1+(6k+1)ψ6k+1

ψfq_k=-(6k-1)ψ6k-1+(6k+1)ψ6k+1

(5)

式中:ψ1,ψ6k±1为转子磁通基波和谐波幅值，具体数值由试验获得见表2；Ld,Lq为电机d,q轴电感，对应转矩项为磁阻转矩，对于表贴式永磁同步电机可认为Ld=Lq，磁阻转矩为零，因此在后续分析中忽略该项；id,iq为d,q轴电流，由三相电流经dq/abc变化得到，对于式(3)所示的包含谐波的相电流信号，经过如下变换为

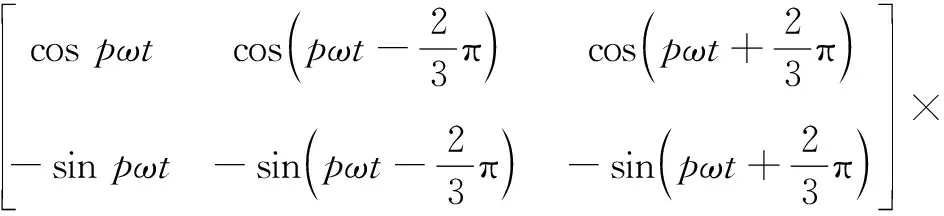
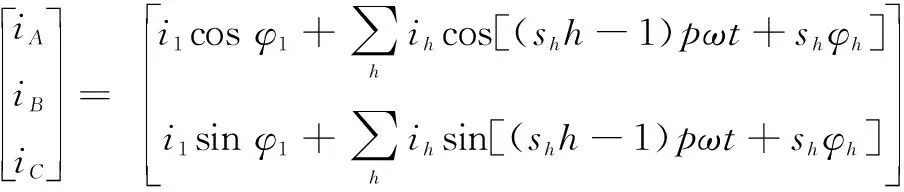
(6)

由于实测的各阶电流信号均为顺相序，因此sh=1。将式(6)代入式(4)可得考虑转子磁场非正弦分布和顺相序电流谐波的电磁转矩解析表达式为

Te=1.5p×

(7)

4.2 转矩波动阶次来源分析

由式(7)可知，转矩波动主要阶次有(h-1)p,6kp,(6k-h+1)p以及(6k+h-1)p阶，其中(h-1)p阶转矩波动由hp阶电流谐波和转子磁通基波相互作用产生；6kp阶转矩波动由电流基波和转子磁通谐波相互作用产生；(6k-h+1)p和(6k+h-1)p阶转矩波动由hp阶电流谐波和转子磁通谐波相互作用产生。根据实测的空载反电动势可知转子磁通中主要阶次为5p和7p阶，更高次谐波幅值较小可以忽略，因此在分析中只关注转子磁通引起转矩波动6p及其相关阶次(即令k=1)；根据实测的负载相电流可知电流信号中主要存在0.8p,1.2p,0.6p和1.4p电流谐波，因此令h=0.8,1.2,0.6和1.4可知该轴向磁通电机转矩波动阶次主要有0.2p,0.4p,5.8p,6p和6.2p，对阶次来源汇总如表4所示。

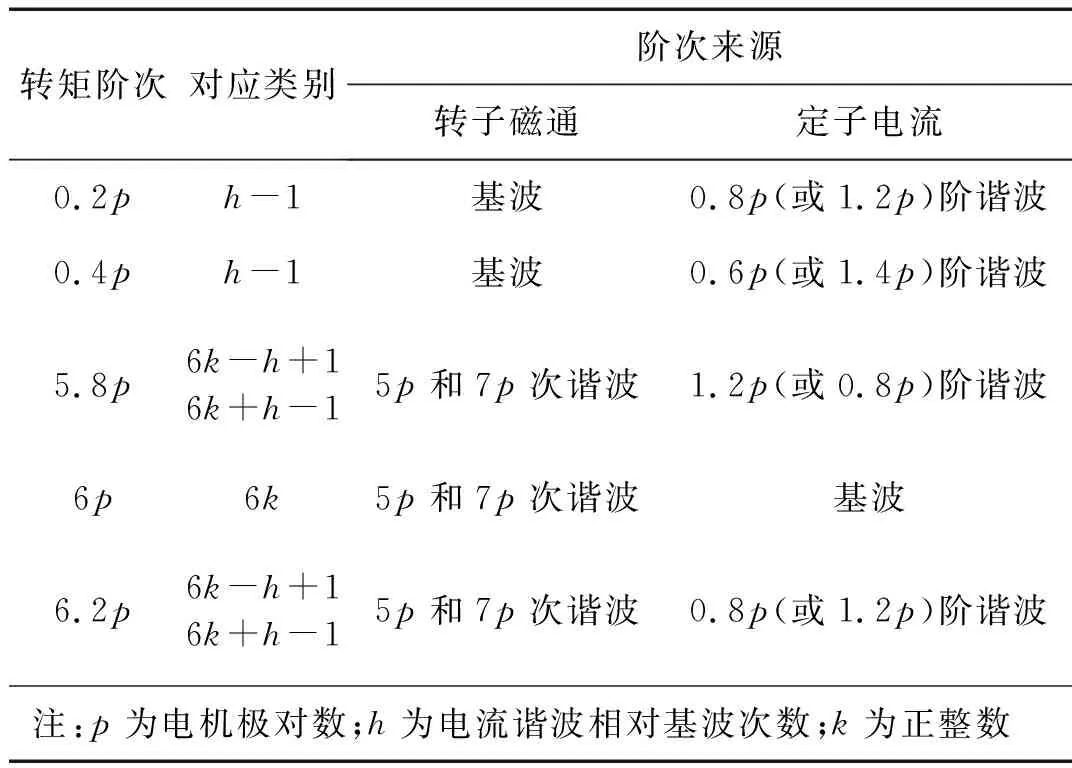
表4 转矩波动阶次来源分析

4.3 基于试验数据的转矩波动幅值预测

为能够有效优化由转矩波动引起的电动轮系统振动，有必要确定转矩波动的主要贡献因素，为此对转矩波动主要阶次幅值进行预测以定量分析转矩波动的全貌。

结合式(7)及表3中100 r/min下相电流幅值相位信息对各阶转矩波动进行计算：0.2p阶转矩波动对应频率为5 Hz，根据其来源可确定幅值为0.8p阶电流谐波和1.2p阶电流谐波与转子磁通基波产生的转矩波动矢量和，即

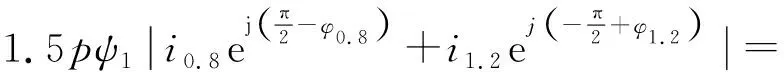
2.143 Nm

(8)

同理可确定0.4p阶转矩波动(10 Hz)幅值为

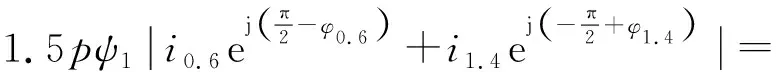
5.032 Nm

(9)

6p阶转矩波动对应频率为150 Hz，根据其来源确定幅值为d，q轴转子磁链谐波矢量叠加，即

(10)

5.8p阶转矩波动对应频率为145 Hz，根据其来源可确定幅值为0.8p阶电流谐波和1.2p阶电流谐波与转子磁通谐波产生的转矩波动矢量和，即

1.833 Nm

(11)

同理可确定6.2p阶转矩波动(155 Hz)幅值为

2.015 Nm

(12)

根据各阶次对应频率和幅值大小可确定电机在100 r/min驱动负载工况下转矩波动情况如图8所示，由图可知，由0.6p阶(或1.4p阶)电流谐波和转子基波磁通相互作用产生10 Hz转矩波动幅值最大，尽管0.8p和1.2p阶电流谐波幅值要明显大于0.6p和1.4p阶，但由于电流谐波相位的关系，0.6p和1.4p阶电流谐波引起的转矩波动相互叠加，而0.8p和1.2p阶电流谐波引起的转矩波动相互抵消，导致10 Hz(0.4p阶)转矩波动相较5 Hz(0.2p阶)显著；另外5.8p和6.2p阶转矩波动要大于6p阶，尽管6p阶转矩波动由转子磁通谐波和电流基波产生，而5.8p和6.2p阶由转子磁通谐波和电流谐波产生，但由于该电机具有丰富的分数阶谐波，谐波相互叠加使其影响较基波更为突出。

为直观分析电流谐波和转子磁通谐波对转矩波动的贡献，按各阶次来源进行分类如表5所示，对于该轮毂电机而言，电流谐波是影响转矩波动的主导因素，为有效降低转矩波动应该着重削弱电机供电电流谐波，特别地，为有效降低幅值最大的0.4p阶转矩波动应该调整0.6p和1.4p阶电流谐波相位关系使二者的影响相互抵消。

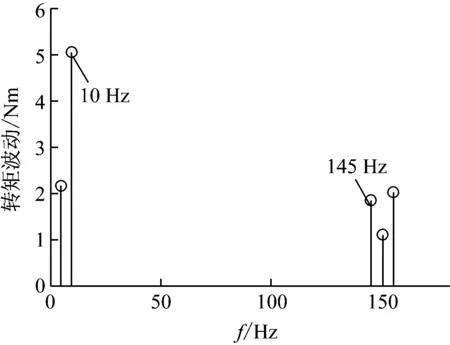
图8 电机100 r/min时转矩波动

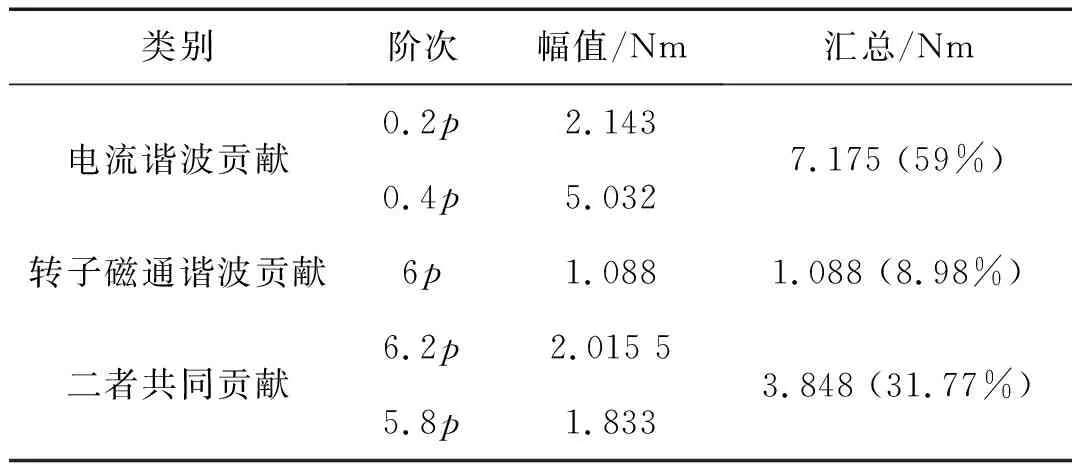
类别阶次幅值/Nm汇总/Nm电流谐波贡献0.2p0.4p2.1435.0327.175 (59%)转子磁通谐波贡献6p1.0881.088 (8.98%)二者共同贡献6.2p5.8p2.015 51.8333.848 (31.77%)

4.4 基于振动加速度信号的转矩波动试验验证

受轮毂电机安装条件和试验成本的限制无法布置转矩传感器以实时测量轮毂电机电磁转矩，由于电机转矩波动将通过轮胎/车轮系统引起电动轮纵向振动，因此本文通过在轮心处布置加速度传感器测量电动轮纵向振动信号以间接反映轮毂电机转矩波动。图9为电机在100 r/min驱动负载工况下轮心处振动加速度频谱，与图8中转矩波动频谱对比可知，电动轮振动存在丰富的振动峰值，两处主要的振动峰值频率为10 Hz和145 Hz，分别对应转矩波动0.4p和5.8p阶。0.4p阶转矩波动幅值最大，因此引起的振动也最大，5.8p阶在100 r/min工况下对应的频率与轮胎固有频率相接近，因此相较其他阶次引起的振动也比较突出。电机相电流中还存在大量除(1±0.2k)p阶的谐波成分会引起丰富的转矩波动阶次，进而在电动轮振动中有所体现，但由于这些谐波幅值相对较小，对振动影响较弱，因此在本文中没有进行分析。通过实测振动加速度信号与转矩波动主要峰值及频率的对比验证了转矩波动阶次分析和幅值预测的准确性，为转矩波动的抑制和电动轮振动的优化提供了参考。

根据永磁同步电机工作原理可知其转矩来源于永磁体产生的旋转磁场和交变相电流产生的电枢反应磁场的相互作用。本文分别通过空载和负载试验识别了与两部分磁场相关的参数，进而定量确定了转矩波动

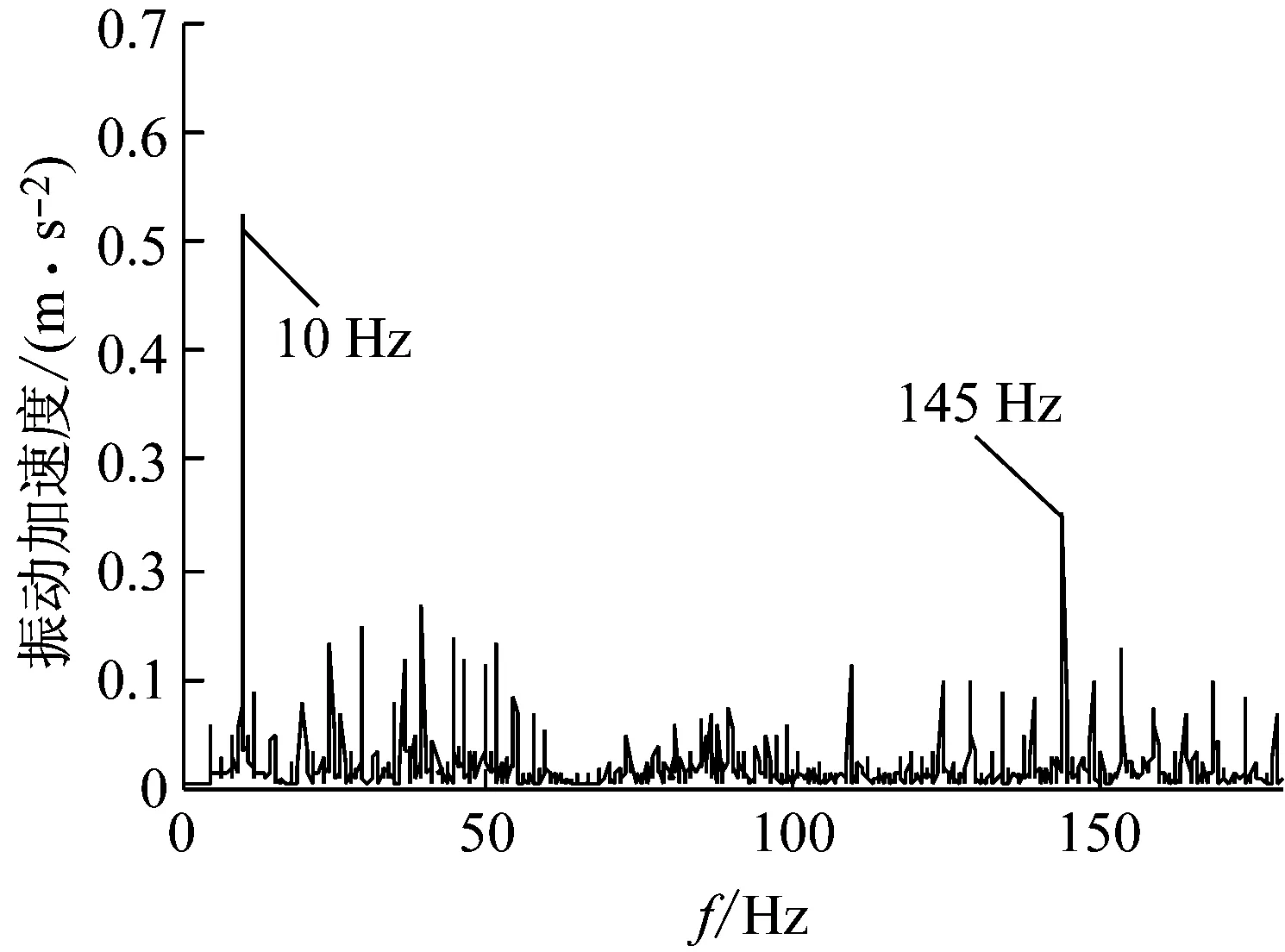
图9 电机100 r/min时电机振动加速度

来源及其大小。该方法不依赖于电机的具体结构和尺寸，也不受电机控制系统的影响。对于永磁同步电机具有一般性和通用性。通过本文试验所采用的轮毂电机实例验证了方法的有效性。

5 结 论

(1) 基于实测的电流谐波阶次能够对转矩波动阶次进行分析：控制器供电下的轮毂电机存在丰富的顺相序分数阶电流谐波，其中hp阶顺相序电流谐波和转子基波磁通相互作用会引起(1-h)p阶转矩波动；hp阶电流谐波和转子磁通谐波相互作用产生(6k-h+1)p和(6k+h-1)p阶转矩波动。(p为电机极对数，h为电流谐波次数，k∈N)

(2) 通过实测转鼓倒拖下的电机空载反电动势识别电机转子磁通基波及谐波成分，并结合实测的相电流谐波幅值和相位能够对主要阶次的转矩波动幅值进行预测，该方法避免了有限元计算的复杂性并且便于直观获得转矩波动全貌及主要因素的影响机理及规律，其有效性通过对比试验结果间接得到了验证。本文的分析方法为永磁同步电机的转矩波动抑制和电动轮系统振动特性的改善提供了优化方向。