基于车-桥随机振动模型的简支梁桥墩顶垂向动反力特征研究
2018-08-27朱志辉黄承志王力东余志武蔡成标
朱志辉, 黄承志, 王力东, 时 瑾, 余志武, 蔡成标
(1. 中南大学 土木工程学院, 长沙 410075; 2. 中南大学 高速铁路建造技术国家工程实验室, 长沙 410075;3. 北京交通大学 土木建筑工程学院, 北京 100044; 4. 西南交通大学 牵引动力国家重点实验室, 成都 610031)
随着高速铁路的快速发展以及城市规模的日益扩大,大量高架线路通过城市密集居民区、工业区等振动敏感点,高速列车带来的环境振动问题日益严重[1]。列车在高架线路上运行时,动载作用通过梁体、支座传递至桥墩,相邻桥墩墩顶垂向动反力以列阵点振源的方式引起环境振动,并进一步诱发附近地下结构以及周边建筑物的二次振动及噪声[2-3]。国内外的学者在开展高架轨道交通列车运行引起的环境振动问题时,通常采用两种计算模型。一种是列车-桥梁-墩-桩-土-临近建筑物整体耦合动力学模型,这种模型虽然从理论上更为接近实际,但由于自由度过于庞大,往往计算效率较低,制约了这种方法的广泛应用;第二种模型采用两步法开展研究[4],首先确定墩顶动反力,然后把墩顶动反力施加在桩基-土体模型上计算环境振动,这种方法由于简化了建模难度,提高了计算分析效率,但采用该方法最关键的问题是确定合理的墩顶动反力计算模型。
Cao等[5]采用半解析数值方法求解了列车通过连续梁时的墩顶反力,以此反力计算结果为输入量分析了列车引起的大地振动特征;Wu等[6]采用半解析方法推导了一系列移动荷载作用下简支梁桥墩顶反力;边学成采用动力子结构法,研究了高速列车运动荷载作用下高架桥-群桩基础-周围场地土振动问题;蒋通等[7]采用简化的车桥系统模型计算了墩顶动反力。以上学者的研究常采用简化的车桥动力分析模型或移动力来求解高架桥墩顶反力,较少考虑高速铁路列车、轨道和桥梁相互作用特征。
时瑾等[8]将钢轨模拟为离散点支撑欧拉梁,桥梁采用模态综合法建立运动方程,在考虑梁-轨和轮-轨关系基础上建立了车桥动力分析模型,并结合常用跨度简支箱梁特点,分析了轨道不平顺、速度和跨度对墩顶动反力的影响规律。但是,该文献以某一确定轨道不平顺样本作为轮轨激扰输入,没有考虑轨道不平顺随机性引起的墩顶动反力统计学特征。 Lu等[9]指出轨道不平顺是一个随里程变化的随机过程,由此引起的列车-结构耦合振动也是一个随机过程,应该采用随机振动的方法进行研究。王贵春等[10-11]研究表明,基于少量样本的时程分析结果,通过统计处理来判别列车、结构的动力性能缺乏可靠性。Zhu等[12]对比分析了Monte Carlo法和虚拟激励法(Pseudo-Excitation Method, PEM)的计算精度和效率,研究发现,PEM方法具有更高的计算效率和计算精度。
因此,本文基于PEM和有限元分析方法,建立列车-轨道-桥梁耦合时变系统竖向随机动力学模型。以CRH2列车通过五跨32 m预应力混凝土简支箱梁桥为例,分析了墩顶动反力随机特征,并研究了轨道不平顺谱种类和列车运行速度对墩顶动反力随机特征的影响。为以后进一步研究环境振动、墩顶动刚度以及支座参数提供前期研究积累。
1 列车-轨道-桥梁动力学模型
1.1 列车模型
由于墩顶动反力主要由列车垂向作用引起,故本文仅考虑列车竖向振动自由度,每节车共有10个自由度。列车的运动方程如式(1)所示
(1)
式中:Mv,Cv,Kv,Xv分别为列车子系统质量矩阵、阻尼矩阵、刚度矩阵和位移列向量;Fv为列车子系统的外荷载列向量。
1.2 轨道-桥梁模型
在车桥耦合系统相互作用研究中,为降低计算工作量,常采用模态叠加法建立桥梁动力方程[13]。考虑轨道结构时,通常在选取模态时难以全面考虑轨道结构局部高频振动模态,从而无法准确计算钢轨局部振动以及轮轨之间的相对位移。采用有限元直接刚度法组装整体刚度矩阵时,由于不存在人为设定分析截止频率问题,计算精度较高。因此,本文采用有限元直接刚度法建立如下所示的轨道-桥梁系统动力方程
(2)
式中:Mb,Cb,Kb,Xb分别为轨道-桥梁子系统的总体质量矩阵、阻尼矩阵、刚度矩阵和位移矩阵,可以直接从通用有限元软件ANSYS中直接导出[14]。其中阻尼矩阵Cb包括桥梁阻尼和轨下弹簧-阻尼器单元阻尼,采用Rayleigh阻尼来模拟桥梁结构的阻尼特性,阻尼比取2%[15]。Fb为轨道-桥梁子系统所受外力列向量。建立的车-轨-桥动力分析模型如图1所示。

图1 列车-轨道-桥梁耦合振动模型
1.3 轨道不平顺模型
为分析不同轨道不平顺条件对车致墩顶垂向动反力的影响,本文采用我国高速铁路无砟轨道不平顺谱(Chinese High-Speed Railways Ballastless Track Irregularity Spectrum, CHBI)、美国六级轨道谱(Federal Railroad Administration (FRA) Track Class 6, FAR6)、德国低干扰轨道谱(German Track Spectrum of Low Irregularity, GLI)和德国高干扰轨道谱(German Track Spectrum of High Irregularity, GHI)高低不平顺作为轮轨激励输入。其中,FAR6,GLI和GHI的具体表达式可参考文献[16]。CHBI则根据我国规范《高速铁路无砟轨道不平顺谱》(TB/T 3352—2014)的规定,采用分段拟合方式得到适用于我国线路速度300~350 km/h的高速铁路无砟轨道不平顺谱。
1.4 轮轨接触模型
列车子系统和轨道-桥梁子系统之间通过轮轨接触关系实现耦合作用。目前处理轮轨垂向接触关系主要存在两种方法[17]:一种是忽略轮轨相对变形的密贴模型;另一种是考虑轮轨相对变形的Hertz接触模型。
密贴模型虽然理论上较为简单,但由于其忽略了轮轨之间的相对变形而难以真实反映轮轨之间的动态相互作用。因此,本文采用线性Hertz接触模型模拟轮轨关系,其中轮轨接触刚度系数根据式(3)求解[18]
(3)
式中:G为轮轨接触常数,m/N2/3;P0为静轮重,N。
2 基于虚拟激励法的墩顶动反力计算
2.1 列车-轨道-桥梁耦合时变系统随机振动分析
将列车子系统和轨道-桥梁子系统通过轮轨接触关系组成整体耦合时变系统,可建立列车-轨道-桥梁耦合时变系统动力方程
(4)

列车-轨道-桥梁耦合系统所受外荷载F(t)包括列车自重引起的确定性荷载Fg和轨道不平顺引起的随机性荷载Fr(t),即
(5)
基于随机振动理论,可将随机激励Fr(t)表示为
Fr(t)=Γ(t)G(t)x(t)
(6)
G(t)=
diag[g(t-t1)] …g(t-tj) …g(t-tn)
(7)
x(t)=
[x(t-t1) …x(t-tj) …x(t-tn)]T
(8)
式中:Γ(t)为作用力指示向量;G(t)为慢变均匀调制函数矩阵;x(t)为轨道不平顺引起的多点异相位平稳随机激励向量;n为列车子系统轮对总数。

(9)
V(t)=diag[e-iωt1… e-iωtj… e-iωtn]
(10)
Q=[1 … 1 … 1]T
(11)
可快速获得系统随机响应的功率谱密度矩阵Suu(ω,t)
(12)
其中,
(13)
式中:h(t-τ,τ) 为脉冲响应函数;Sxx(ω)为x(t)的自谱密度矩阵。最后,根据随机响应的功率谱密度矩阵,可通过下式求得系统随机响应的均方根
(14)
式中:Δω为频率增量。
考虑由车轮间距所产生的轮轨间随机激励相位差,第j(j=1~n)轮对由轨道不平顺引起的虚拟轨道不平顺rj可以表示为
(15)

(16)
式中:ω为轨道不平顺的时间圆频率,rad/s;λ为轨道不平顺函数谐波分量的波长,m。
2.2 墩顶动反力
列车行驶过程中,桥墩墩顶垂向动反力F可写为
F=KZΔx+CzΔv
(17)
式中:KZ为墩顶弹簧阻尼器竖向刚度;Cz为阻尼系数;Δx和Δv分别为弹簧阻尼器顶端与底部位移之差和速度之差。高速铁路常用支座类型有盆式橡胶支座、球形钢支座及特殊要求支座等,支座系统本身力学行为复杂。文献[19]研究表明,不同的支座恢复力模型对动载竖向力传递影响不大;文献[20]指出实际弹性支座计算条件下,支座弹性对桥梁和车体的振动影响不明显,因此本文模型中支座采用了刚性支撑。根据2.1节可求得墩顶动反力F的随机响应均值μF与随机响应均方根σF。
工程设计中,随机响应最大值通常为重点关注对象。本文采用3σ法则(即μ±3σ)确定列车-轨道-桥梁耦合系统墩顶动反力随机特征的上、下限值。同时,根据上述列车-轨道-桥梁耦合时变系统随机分析方法,本文开发了相应的MATLAB计算程序,具体计算流程如图 2所示。

图2 基于虚拟激励法的车-桥耦合系统随机振动分析流程图
3 算例验证
3.1 轨道-桥梁整体有限元模型
以我国高速线路总里程中占比最大的32 m标准跨度双线单箱型截面预应力混凝土简支梁桥为研究对象,桥梁铺设双块式无砟轨道,双块式无砟轨道主要由钢轨、扣件、预制的双块式轨枕、混凝土道床板等组成。双块式无砟轨道中,轨道的弹性主要靠轨下胶垫来提供。由于轨枕和混凝土道床板完全联结在一起,轨下基础的质量很大,道床板与混凝土底座之间基本没有弹性,故双块式无砟轨道的振动主要体现在钢轨的振动,而轨枕和道床板的作用可通过参振质量的形式在桥梁动力学模型中加以考虑。因而将轨道板与桥梁考虑为整体进行模拟,钢轨和桥梁间通过等间距布置的扣件相连接,将轨下结构对钢轨的支撑作用采用轨下支撑弹簧模拟。
采用有限元方法建立如图 3所示的无砟轨道-桥梁模型,主梁和桥墩截面如图 4所示。在有限元模型中,钢轨、主梁和桥墩均采用空间梁单元模拟。为了考虑桥梁的高频振动,本文主梁单元长度为0.6 m,保持与扣件间距一致,轨道结构节点和桥梁节点在扣件位置处一一对应,按节点位移协调处理。线路偏心通过刚臂考虑,钢轨节点和刚臂节点之间采用弹簧-阻尼器联结,考虑轨下扣件和垫板的弹性支撑作用,垂向刚度和阻尼分别为4.76×107N/m和7.5×104N·s/m,横向刚度和阻尼分别为2.5×107N/m和6×104N·s/m,桥面二期恒载取160 kN/m。

图3 轨道-桥梁系统有限元模型
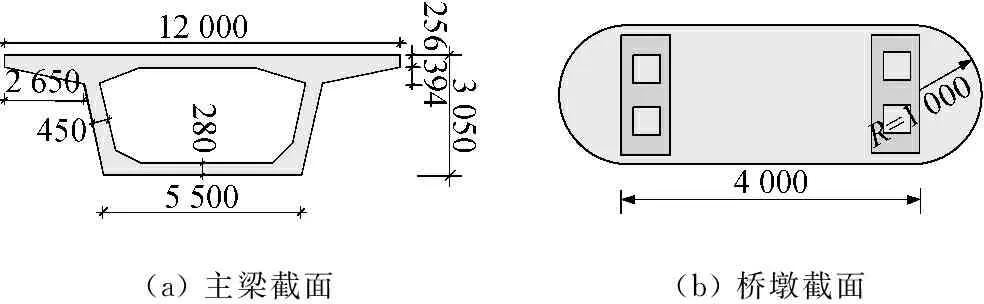
(a) 主梁截面(b) 桥墩截面
图4 桥梁截面示意图(单位:mm)
Fig.4 Schematic diagram of bridge section (unit: mm)
3.2 验 证
参考文献[21],采用自编程序开展ICE3高速列车通过该桥梁模型的车-桥耦合振动响应计算。列车编组模式为按8车编组(2M+6T),头车和尾车为轴重较大的动车,其余6辆均为轴重较小的拖车,列车详细参数见朱志辉等的研究,行车速度为250 km/h,轮轨间激扰采用由德国高速铁路低干扰谱变换出的轨道不平顺时域样本。将计算结果与文献[21]的结果进行对比来验证模型及程序的正确性。
图 5和图 6分别给出了图 3中③号桥墩墩顶垂向位移和垂向加速度的结果,从图中可以看出本文和文献[21]的结果在幅值和趋势上吻合良好。其中由于原文没有给出详细的列车、轨道、桥梁参数,本文算例中所选取车-线-桥模型相关参数与文献[21]存在差别,导致本文的墩顶垂向位移偏小。总体而言,本文计算方法能够较好的反映车-轨-桥耦合振动特性,满足工程应用要求。

图5 桥墩墩顶垂向位移

图6 桥墩墩顶垂向加速度
4 计算结果与分析
4.1 墩顶动反力随机特性分析
基于列车-轨道-桥梁耦合系统随机动力学模型,选取八车编组CRH2列车以300 km/h的速度单线通过简支梁的计算结果,对墩顶垂向动反力的随机特征进行研究。其中轨道不平顺为德国低干扰轨道不平顺谱,波长范围为1~100 m,相应的频率计算范围为0.833~83.3 Hz,频域积分步长为0.833 Hz。以图 3中的③号墩为例,桥墩顶部受到墩顶动反力F1,F2作用,如图 7所示。

图7 ③号墩墩顶动反力示意图
图 8给出了3号墩墩顶动反力F1,F2以及合力F的统计参数时程曲线。其中μ为不考虑轨道不平顺时车-桥耦合振动引起墩顶动反力均值,σ为轨道不平顺引起的墩顶动反力均方根,(μ±3σ)为基于3σ法则的墩顶动反力上、下限值。
从图 8可以看出
(1) 墩顶动反力受确定性激励(列车轴重)控制,其中随机激励引起的墩顶动反力均方根σ最大值约为确定性激励引起的墩顶动反力均值μ最大值的8%。
(2) 从图 8(c)中可知,根据3σ法则计算的墩顶动反力下限值(μ-3σ)F和上限值(μ±3σ)F的最大值分别为606.18 kN和875.37 kN,变化幅度为269.19 kN;相对于墩顶动反力均值μF最大值的变化在-17.76%~18.76%。
(3)F1和F2的动力响应指标(均值与均方根)差别很小,振动趋势类似,但是由于列车通过相邻两跨简支梁的时间先后不同,F1和F2的动力响应之间存在一定的相位差,因此合力F和分力F1,F2之间的统计参数不具有简单的倍数叠加关系。
为了节省篇幅,只选取第3跨简支梁对③号墩引起的墩顶动反力F1做频域分析。通过对图 8 (a)中的F1做快速傅里叶变换(Fast Fourier Transformation, FFT),可以得到F1均值(μF1)的功率谱密度(Power Spectral Density Function, PSD)曲线,如图 9所示;图 10中给出了基于虚拟激励法得到的随机激励下F1的时变PSD云图。
从图 9可知,当车速为300 km/h时,主频f1=0.208 Hz,(1/f1)与列车通过全桥的加载时间t一致;同时,列车车长加载频率fv=f2(fv=v/lv=3.27 Hz[22],

(a) μ

(b) σ

(c) μ±3σ
v和lv分别为车速和列车长度),说明列车车长的周期性激励对墩顶动反力影响较大。从图 10可知,随机荷载激励下墩顶动反力的主频大致分布在两个连续的宽频0.83~8 Hz和25~48 Hz内,分别与列车车长引起的周期性加载频率(fv=3.27Hz),列车轴距引起的周期性加载频率(ft=v/lt=3.3 Hz,lt为列车轴距)密切相关。
4.2 轨道不平顺对墩顶动反力的影响
由上一节分析可知,轨道不平顺对墩顶动反力影响显著,因此本节通过对比相同车速(300 km/h)条件下,不同轨道不平顺谱引起的墩顶动反力随机响应特征,研究轨道不平顺对墩顶动反力的影响规律。

图9 确定激励下F1的PSD
表 1给出了不同轨道不平顺下F1的统计参数最大值,图 11~图 13分别给出了不同轨道不平顺随机激励下F1的均方根(σ)和限值(μ+3σ)的时程曲线以及PSD云图,从表 1和图 11~图 13的结果中可知
(1) 我国高速铁路无砟轨道不平顺谱引起的墩顶动反力离散性最小,德国高干扰轨道谱引起的墩顶动反力离散性最大,二者均方根(σ)最大值相差40.79 kN,表明轨道不平顺等级越低,墩顶动反力离散性越大;二者墩顶动反力(μ+3σ)最大值相差26.68%。
(2) 不同轨道不平顺下墩顶动反力的均方根时程曲线波形相似,只是幅值大小不同,说明尽管轨道不平顺等级不同,但是列车经过桥梁时,对墩顶动反力造成的离散性随时间的变化规律是一致的。
(3) 比较不同轨道不平顺随机激励下F1的PSD
云图可知,4种轨道不平顺下的墩顶动反力主频分布类似,大致分布在两个连续的宽频范围内,说明同一行车条件下,不同轨道不平顺对墩顶动反力有影响的波长范围相似。

表1 不同轨道不平顺下统计参数最大值

图11 σF1

图12 (μ+3σ)F1
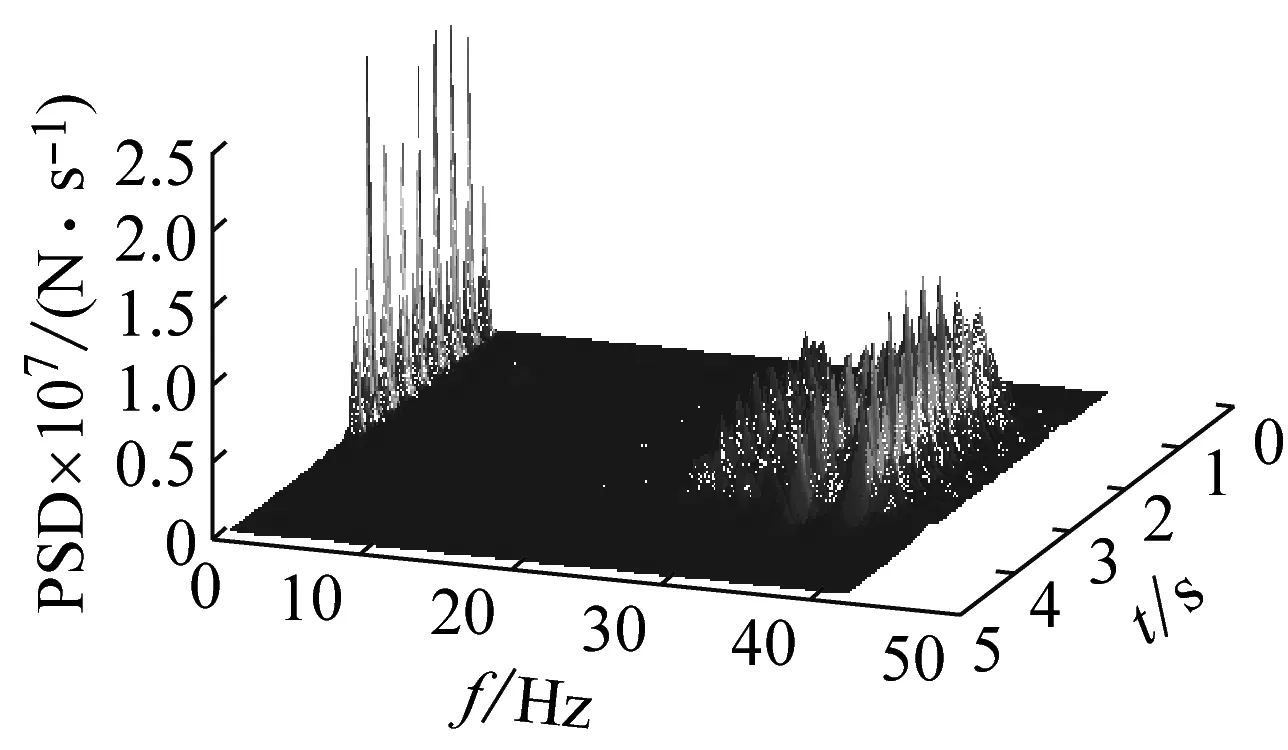
(a) CHBI
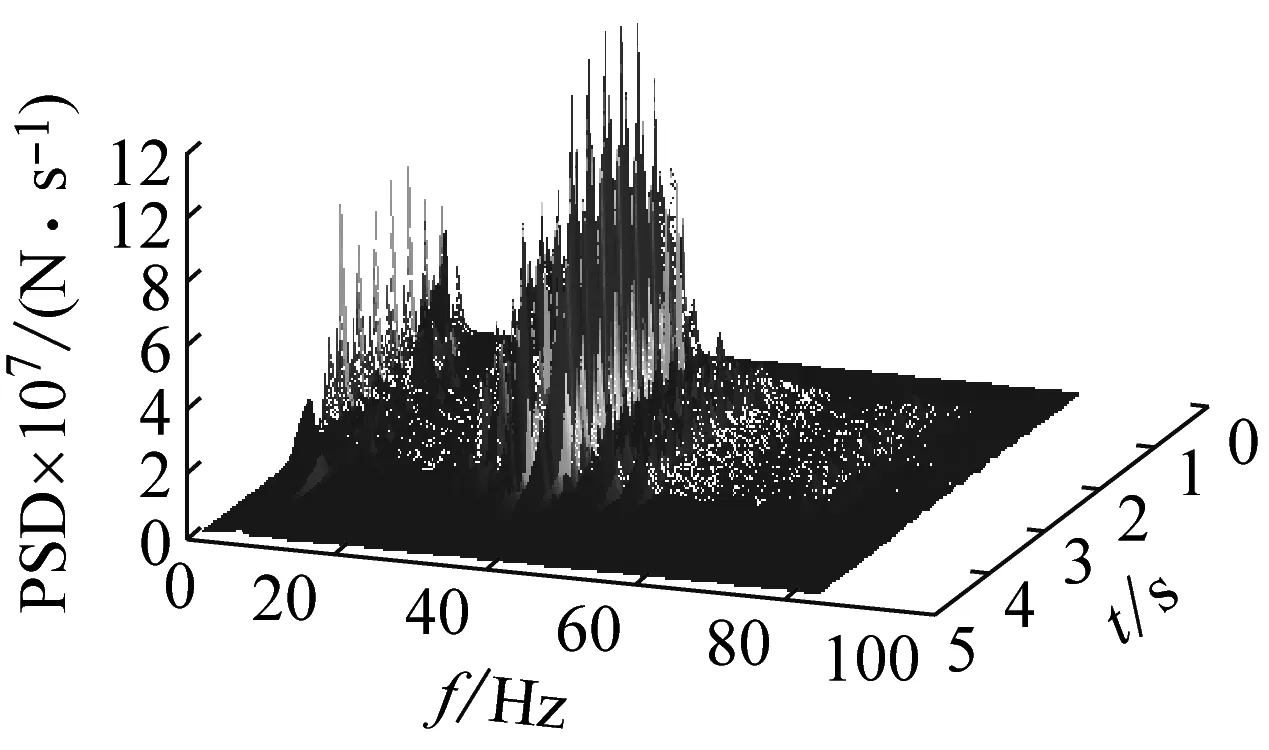
(b) GHI

(c) FAR6
4.3 列车运行速度对墩顶动反力的影响
列车运行速度对车桥耦合系统的动力响应影响显著,为研究墩顶动反力随机特征随车速的变化规律,选取轨道不平顺为德国低干扰,列车以100~500 km/h(按12.5 km/h递增)之间33种不同车速通过简支梁的计算工况来分析。图 14和图 15分别给出了F1的统计参数最大值随车速变化规律和不同车速轨道不平顺随机激励下F1的PSD云图;表 2则给出了不同车速下F1的统计参数最大值。
从图 14、图 15以及表 2的结果中可知
(1) 随着车速的增大,由车-桥耦合振动引起的共振和消振导致桥梁墩顶动反力均值(μ)的最大值被放大和缩小。墩顶动反力限值(μ+3σ)主要受确定性激励响应(μ)控制,所以其随车速的变化规律与均值(μ)类似。
(2) 墩顶动反力均方根(σ)随着车速的增大而显著增大,当车速从100 km/h增大到500 km/h,均方根从12.6 kN增大到100 kN,表明车速越大,轨道不平顺的影响越大,墩顶动反力的离散性越大。
(3) 车速为100 km/h时,轨道不平顺随机激励下F1的主频分布在0.28~1.39 Hz内,车速为400 km/h时,的主频则分布在1.11~70 Hz内。可以发现车速较小时,墩顶动反力主频主要集中分布在一个低频范围内,只有长波不平顺对其有影响;而随着车速的增大,墩顶动反力主频分布渐渐向高频扩展,趋向于在一个连续的宽频范围内均匀分布,短波不平顺的影响有所体现。

图14 F1的统计参数最大值随车速变化规律

(a) 100 km/h

(b) 200 km/h

(c) 400 km/h

速度/(km·h-1)100150200250300350400450500μ/kN522.4497.2463.4477.7478.9484.1430.1498.7641.0σ/kN12.621.821.732.040.443.355.063.7100.0μ+3σ/kN536.5 560.5521.2568.4593.7610.6577.9658.4930.7
5 结 论
本文基于虚拟激励法和有限元法,建立了列车-轨道-桥梁耦合系统竖向随机振动模型,并以CRH2列车通过我国高速线路占比最大的32 m预应力混凝土简支箱梁桥为算例,对墩顶垂向动反力随机特性以及轨道不平顺种类和车速对其影响规律进行了研究,得出了如下结论:
(1) 建立了列车-轨道-桥梁耦合系统竖向随机振动模型,可以全面考虑轨道不平顺引起的随机振动,得到墩顶动反力的均值、均方根和限值等统计指标;墩顶动反力受列车轴重确定性激励和轨道不平顺随机激励的双重影响,且受轨道不平顺的影响显著,任意时刻的墩顶动反力并非确定值,而是介于下限值(μ-3σ)和上限值(μ+3σ)之间。
(2) 不同轨道不平顺下,墩顶动反力的均方根(σ)大小不同,轨道不平顺等级越低,离散性越大;随机激励下的墩顶动反力PSD云图主频分布类似。
(3) 随着车速的增大,由车-桥耦合振动引起的共振和消振导致桥梁墩顶动反力均值(μ)的最大值被放大和缩小,特别是共振条件下,墩顶动反力峰值变化剧烈;墩顶动反力均方根(σ)受车速影响显著,车速越大,墩顶动反力离散性越大,从而导致根据3σ法则得到的墩顶动反力限值越大。
