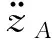基于改进多目标粒子群算法的商用车悬架系统优化
2018-08-27范政武王永红石晋宏
范政武, 王 铁, 王永红, 石晋宏
(1. 太原理工大学 车辆工程系, 太原 030024; 2. 山西大运汽车制造有限公司, 山西 运城 044000)
车辆的动态行为是决定车辆操纵性能和乘坐舒适性的决定性因素。 同时,它还影响施加到道路和车桥的动态载荷,这可能导致对路面的快速损坏和底盘部件的早期故障。 然而,车辆悬架系统参数的确定通常在主要目标之间冲突:乘坐舒适性,操纵性和低动态载荷。 人们在车辆悬架系统参数优化方面作了大量的研究。Els等[1]应用dynamic-Q算法优化车辆的操纵性和舒适性。Gonçalves 等[2]应用柔性多体动力学对公路车辆悬架系统优化,改善其舒适性。Yang等[3]基于多体系统动力学对车辆平顺性进行研究。以上文献通过加权等方式把多目标优化转化为单目标优化, 然后用数学规划的方法来求解, 每次只能得到一种权值情况下的最优解。
近年来,多目标优化算法在车辆悬架系统优化中得到广泛的应用。Nariman-Zadeh等[4]提出了多目标均衡多样性遗传算法(Multi-objective Uniform-diversity Genetic Algorithm,MUGA),对5自由度车辆振动模型进行多目标优化。Mahmoodabadi等[5]提出了粒子群算法和遗传算法的混合算法对5自由度车辆振动模型进行多目标优化。刘伟等[6]提出基于改进遗传算法NSGA-II的悬架系统多目标优化策略。近年来提出了多种改进的算法对悬架参数进行优化[7-9]。遗传算法作为一种高度并行随机全局搜索方法,能较好的找到全局最优,但是收敛速度慢,产生新的后代时间比较长。为了改进优化策略,一个基于群体进化的粒子群优化算法(Particle Swarm Optimization, PSO)提了出来。粒子群优化似乎特别适合于多目标优化,主要是因为算法收敛的高速度。Coello等[10]首次把单目标粒子群拓展应用到多目标问题优化。此后许多学者提出了多种改进多目标粒子群算法[11-16],改善算法的收敛性和解的多样性。
本文提出了一种基于点到直线最小距离的改进多目标粒子群优化算法(Minimum Distance of Point to Line Multi-object Particle Swamp Optimization,MDPL-MOPSO),以改善车辆的平顺性和轮胎动载为目标,对重型商用车悬架系统优化设计。
1 模型建立
若要准确地分析汽车的振动响应,首先应建立合理的动力学模型,模型建立时所考虑因素的多少与计算精度有很大关系,由于汽车各部件振动情况十分复杂,欲通过一个完整的模型全面反映汽车的振动特性是比较困难的。因此,在研究问题时,需根据问题的主次因素,对振动系统进行适当的简化。通过对汽车在行驶过程中能量分布的分析,将6×4牵引列车振动系统简化为1/2汽车12自由度动力学模型,其整车参数表见表1,某6×4牵引车列车12自由度振动力学模型如图1所示。
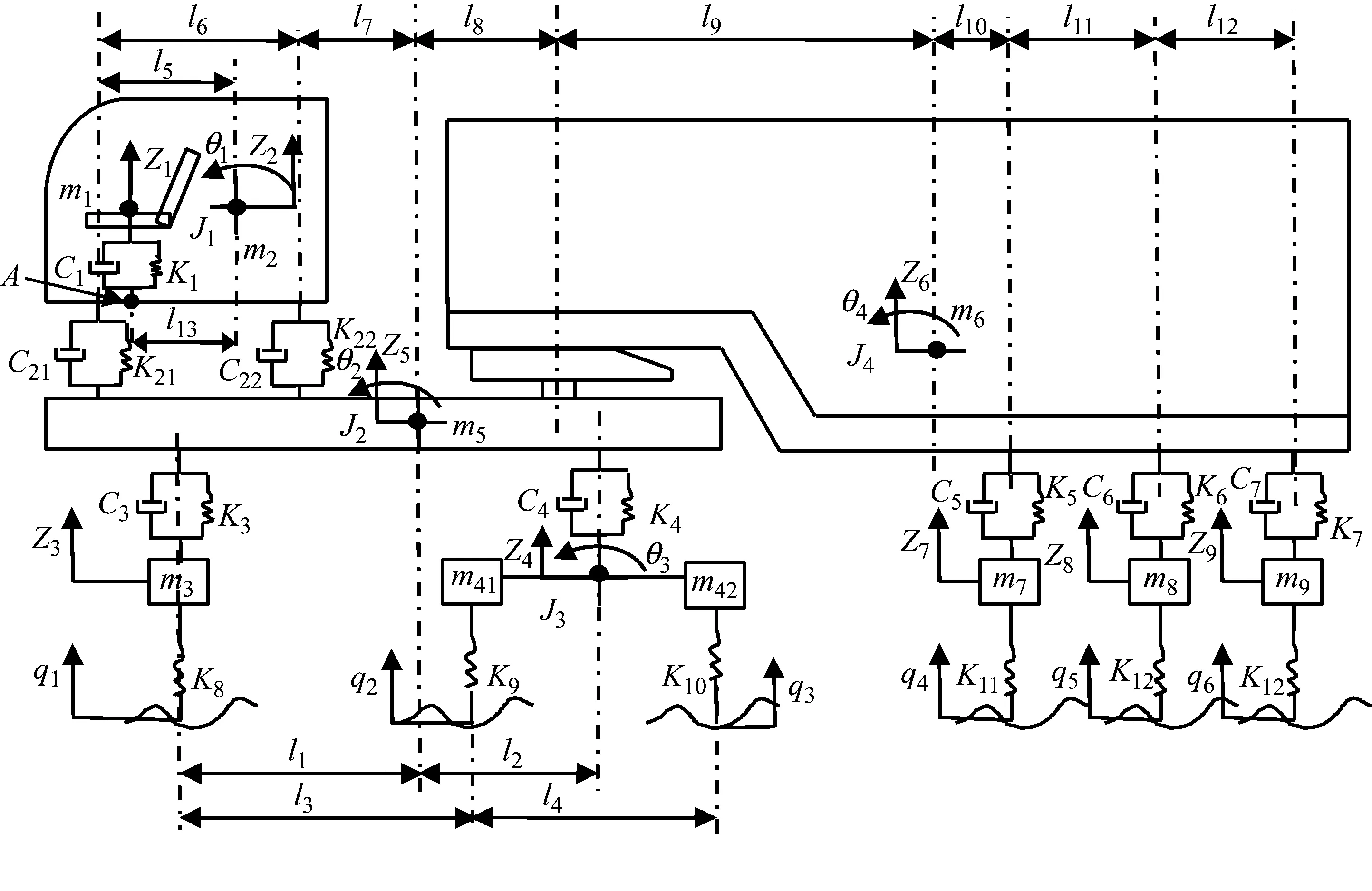
图1 某6×4牵引车列车12自由度振动力学模型
针对本文12自由度振动力学微分方程,系统的动能T、势能U和耗散能D分别如下[17]
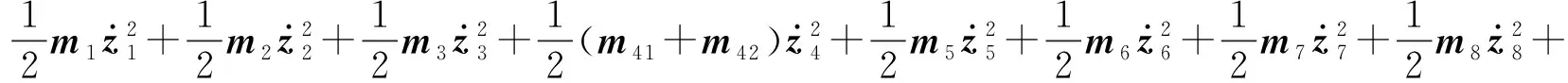
(1)
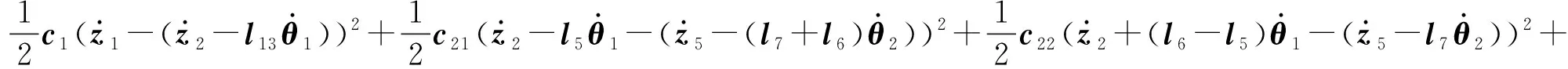
(2)
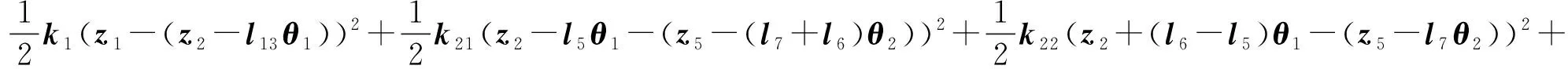
(3)
有阻尼振动系统的自由振动拉格朗日微分方程
(4)
式中:qi为第i个自由度。
把式(1)~式(3)代入式(4)可得
(5)
左右轮辙的不平度相同,汽车对称于其纵轴线,运行时仅考虑垂直振动及俯仰振动,设后面的车轮行驶在前轮的轮辙上。关于路面不平度的模拟可参考文献[18]。
前轴第一轮路面不平度的微分方程为
(6)
式中:n00为路面空间截止频率,n00=0.01 m-1;v为车速,m/s;n0为标准空间频率,n0=0.1 m-1;Sq(n0)为路面不平度系数,Sq(n0)=256×10-6m3(C级路面)[19];W(t)为白噪声。
第i轴的车轮路面输入可写成
qi(t)=q1(t-L1i/v),i=2,3,…,6
(7)
式中:qi(t)为第i轴车轮路面驶入,i=2,3,…,6;L1i为第i轴与第一轴的距离,m。
采用二阶Pade近似计算可求出qi(t)和q1(t)的传递函数,将其转化为状态方程和输出方程
qi=CXi+q1
(8)
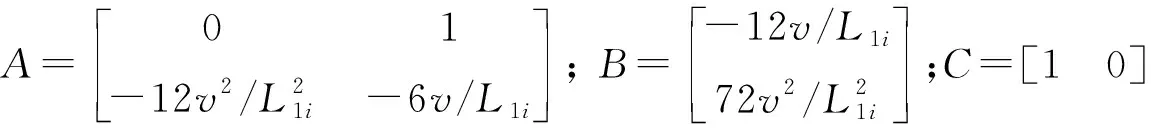
车速40 km/h,牵引车和半挂车车轮的路面激励时域仿真如图2和图3。从图中可以看出,变化波形基本相同,只是时间上滞后。
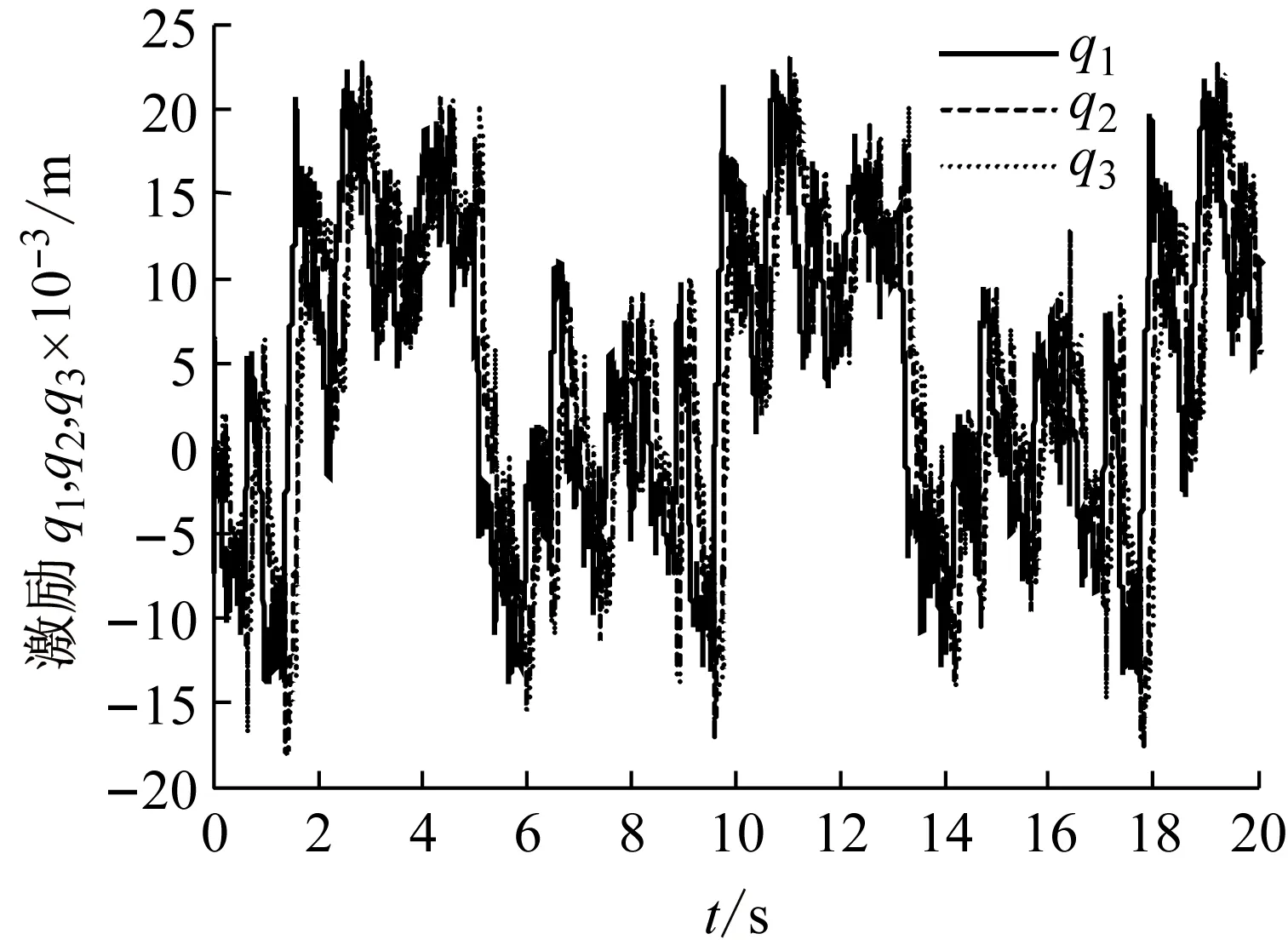
图2 牵引车激励时域模型仿真
2 模型分析
2.1 仿真分析
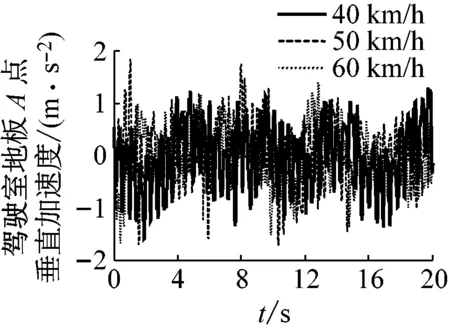
选取B级公路,车速为40 km/h,50 km/h,60 km/h三种车速,仿真不同速度驾驶室底地板A点处垂直加速度,仿真结果如图4和图5所示。
图3 半挂车激励时域模型仿真
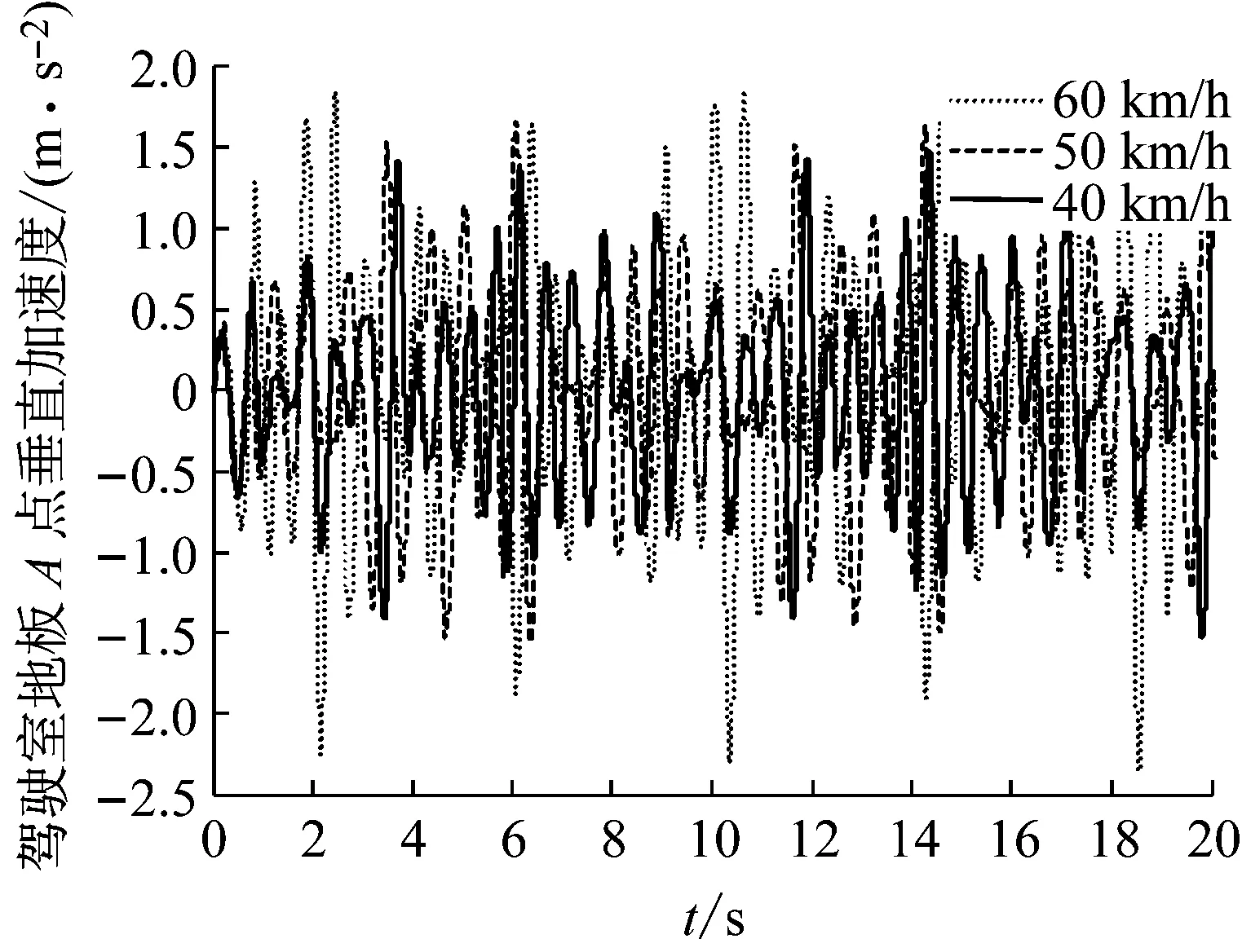
图4 驾驶室地板加速度时域仿真
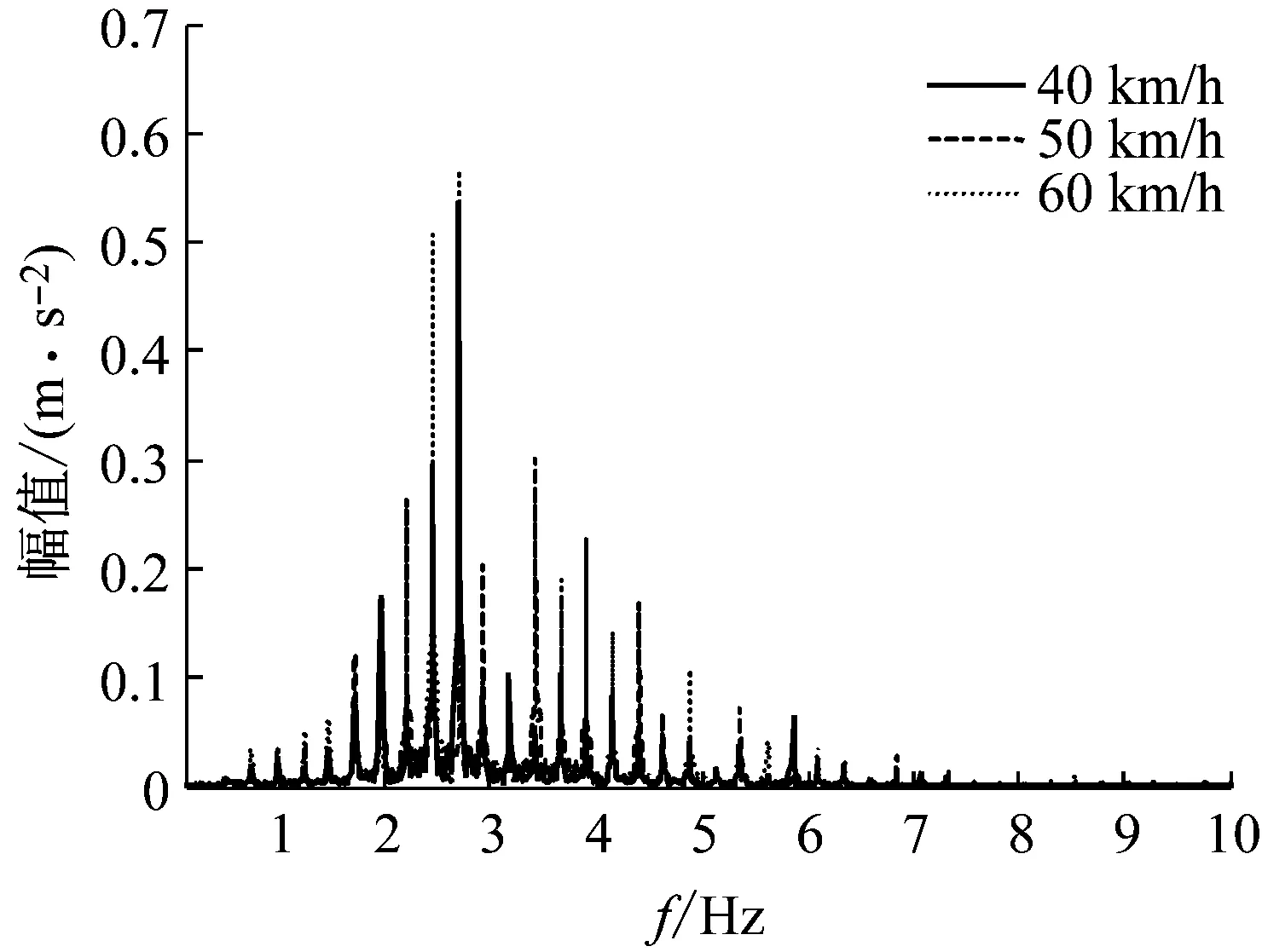
图5 驾驶室地板加速度频域仿真
驾驶室地板A点处垂直加速度表达式为
(9)
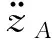
图4为驾驶室地板加速度时域分析,其均方根值 (Root Mean Square, RMS)分别为0.61 m/s2,0.51m/s2,0.53 m/s2,可以看出,在50 km/h时加速度均方根值最小。而根据人体对振动环境的舒适反应[20],在0.315~0.63 m/s2内人体会感到有点不舒服,而0.5~1 m/s2内人体会相当不舒服,三种车速下驾驶室地板加速度均方根值大于0.50 m/s2,接近于0.315~0.63 m/s2内的上限。图5是频域分析,人体在垂直方向最为敏感的频率范围为4~8 Hz,从图中可以看出在4~8 Hz内振动幅值相对较小,在2~4 Hz内振动幅值较大。不同车速下其频率以及对应的幅值如表2。
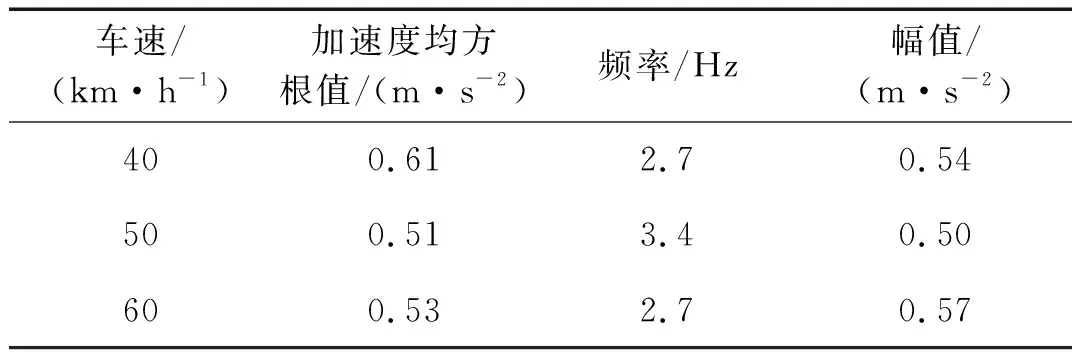
表2 驾驶室地板加速度时域及频域仿真结果
2.2 试验测试
为了获得牵引列车在典型作业状态下的振动响应特征,进行了6×4牵引车带三轴半挂列车实车试验。
试验路面为高速公路,其路面状况如图6所示。全车布置17个测试点,信号测点布置如图6(b)所示。使用北京东方振动噪声研究所研发的DASP系统进行振动数据的数字采样,信号获取使用配套的INV9821传感器,灵敏度为50 mv/g。
试验车辆装载30 t土石方,试验车速为40 km/h,50 km/h,60 km/h。采样频率为25 000 Hz,采样时长为200 s,对试验重复进行了10次。完成数据采集后,根据数据对比结果,由于路面的时变特性,各次数据表现有差异性,但总体趋势一致,选择第三次采样数据为分析样本。

(a) 采集仪
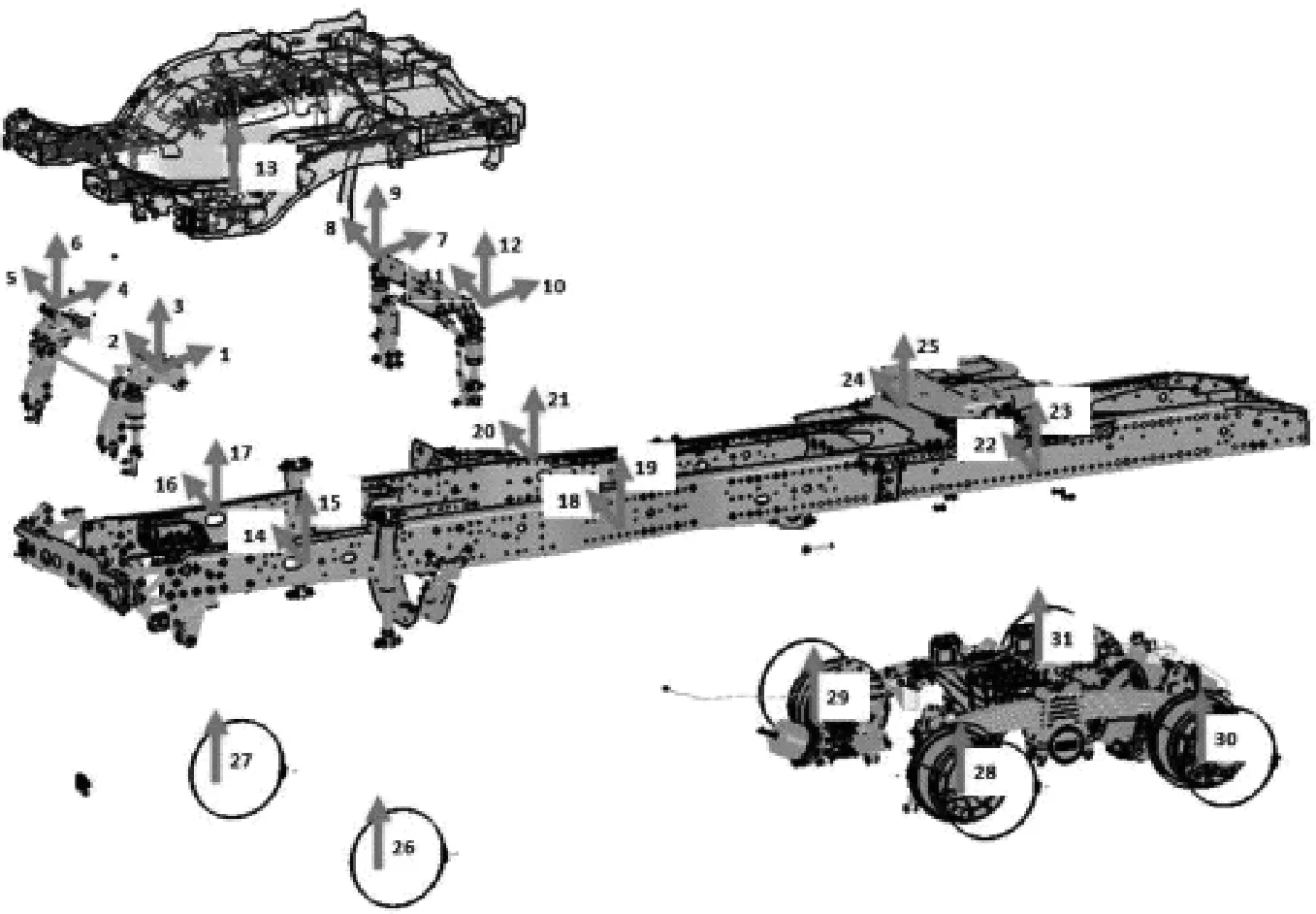
(b) 传感器布置

(c) 试验路况
图7是驾驶室地板加速度在40 km/h,50 km/h,60 km/h三种速度下的试验结果。图7(b)~图7(d) 显示了试验和仿真结果的对比。从对比结果可以看出,试验和仿真的时域信号基本吻合。表3为加速度的均方根值对比,仿真的误差分别是8.9%,1.9%和3.6%。误差较小,其精度可以满足动态分析要求。
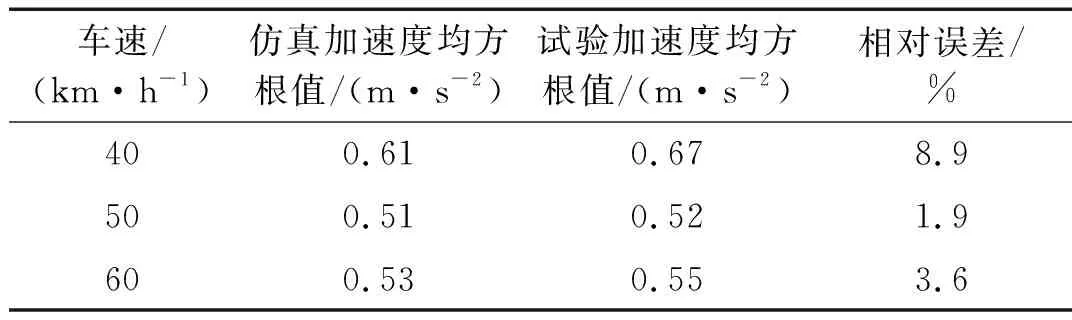
表3 试验与仿真时域分析对比
(a) 车速40 km/h,50 km/h,60 km/h
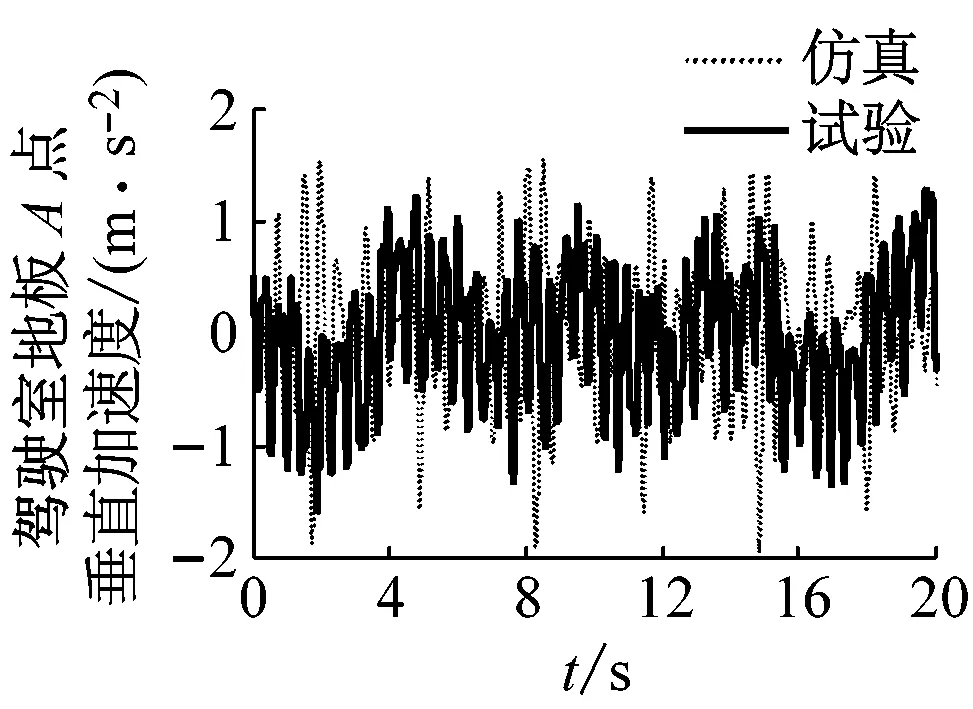
(b) 车速40 km/h试验与仿真对比
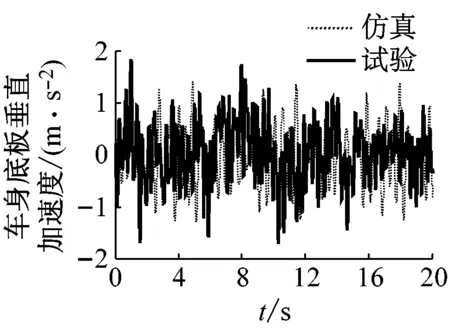
(c) 车速50 km/h试验与仿真对比
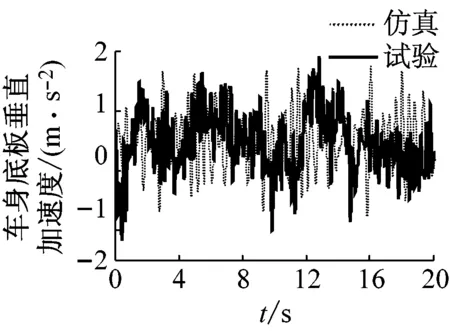
(d) 车速60 km/h试验与仿真对比
图7 驾驶室地板加速度试验与仿真对比
Fig.7 Acceleration test and simulation comparison
3 悬架系统参数多目标优化
3.1 点到直线最小距离多目标粒子群优化算法
在科学研究和工程技术的实践活动中,优化是重要的研究工具。所优化研究的对象多数为多目标优化问题(Multi-objective Optimization Problem,MOP),多目标优化问题可以用下面的公式来表示
MinimizeF(x)=(f1(x),f2(x),…,fm(x))T
x∈Ω
(10)
式中:Ω为变量空间;x为变量矢量。F(x) 包含m个目标函数fi:Ω→R,i=1,…,m,Rm为目标空间。
本文提出了一种点到直线最小距离多目标粒子群优化算法(Minimum Distance of Point to Line Muti-Object Particle Swarm Optimization,MDPL-MOPSO),是一种新的寻找全局最优指导方法。
如前所述,已经存在几种重要的MOPSO方法。在每一种方法中,有不同的寻找全局最优指导的方法。这些方法有一个共同的特点,就是随机选择。在本节中我们介绍一种新的方法来寻找全局最优指导。
下面以两目标空间为例来说明这种方法的机理。
在两目标空间中帕累托前端的某个点H坐标(f1j,f2j)被赋予对应的直线L,L定义如下
(11)
直线外一点P,坐标(f1i,f2i)到直线L距离d定义如下
(12)
当f1j=0,直线L就是轴f2,dij=f1i,当f2j=0,则直线L就是轴f1,dij=f2i,见图8所示。
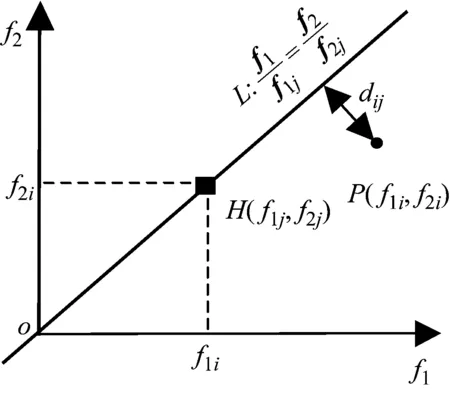
图8 两目标空间点到直线距离
应用点到直线最小距离的方法,按照下面的步骤,在外部存档中为粒子群中每个粒子寻找全局最优指导。首先在目标空间中,给外部存档中每个粒子j定义直线Lj;第二步计算粒子群中粒子i在目标空间中距直线Lj的距离dij。如果外部存档中粒子k的直线与粒子群中粒子i的距离dik最小,则选择外部存档中粒子k作为粒子i的全局最优指导。如图9所示,假设外部存档有3个粒子A,B,C,粒子P选择全局最优指导。粒子P距三条直线的距离d分别是0.97,3.53,7.03,可以看出粒子P距过A点的直线距离最小,因此选着粒子A为全局最优指导。通过这种方法,粒子群中的粒子能够直接飞向外部存档中的粒子,具有很好的收敛性。
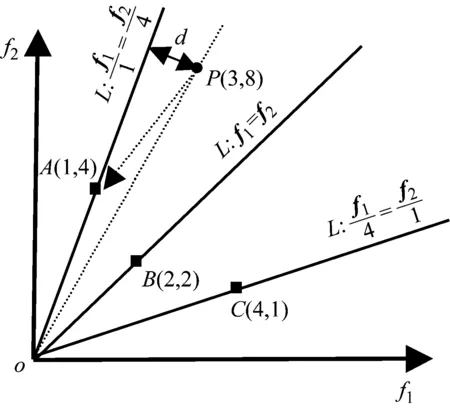
图9 寻找全局最优指导的示例
我们知道,在两条直线形成的夹角区域中,夹角的中分线上的点到这两条直线的距离相等。如图10所示,外部存档中粒子A在目标空间中的直线为L1,粒子B在目标空间中的直线为L2,而直线L是直线L1和直线L2形成的夹角区域的中分线,在直线L上的粒子距直线L1和直线L2的距离d1=d2。直线L把它分成两个区域,M区域和Q区域,在M区域内的粒子选择A为全局最优指导,在区域Q内的粒子选择B为全局最优指导,在直线L上的粒子可随机选择A或B作为全局最优指导。同理,外部存档的其它粒子也是相同的状态。也就是说,应用点到直线最小距离的方法,可以把目标空间分成许多不同的区域,区域内的粒子选择最接近自己的外部存档粒子作为全局最优指导,从而提高帕累托优化前端解的多样性和分布性。
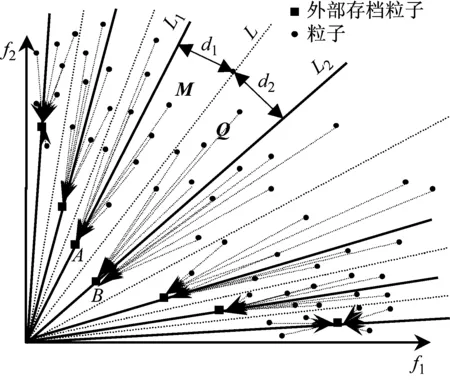
图10 应用点到直线最小距离方法寻找全局最优指导
算法流程图如图11所示。
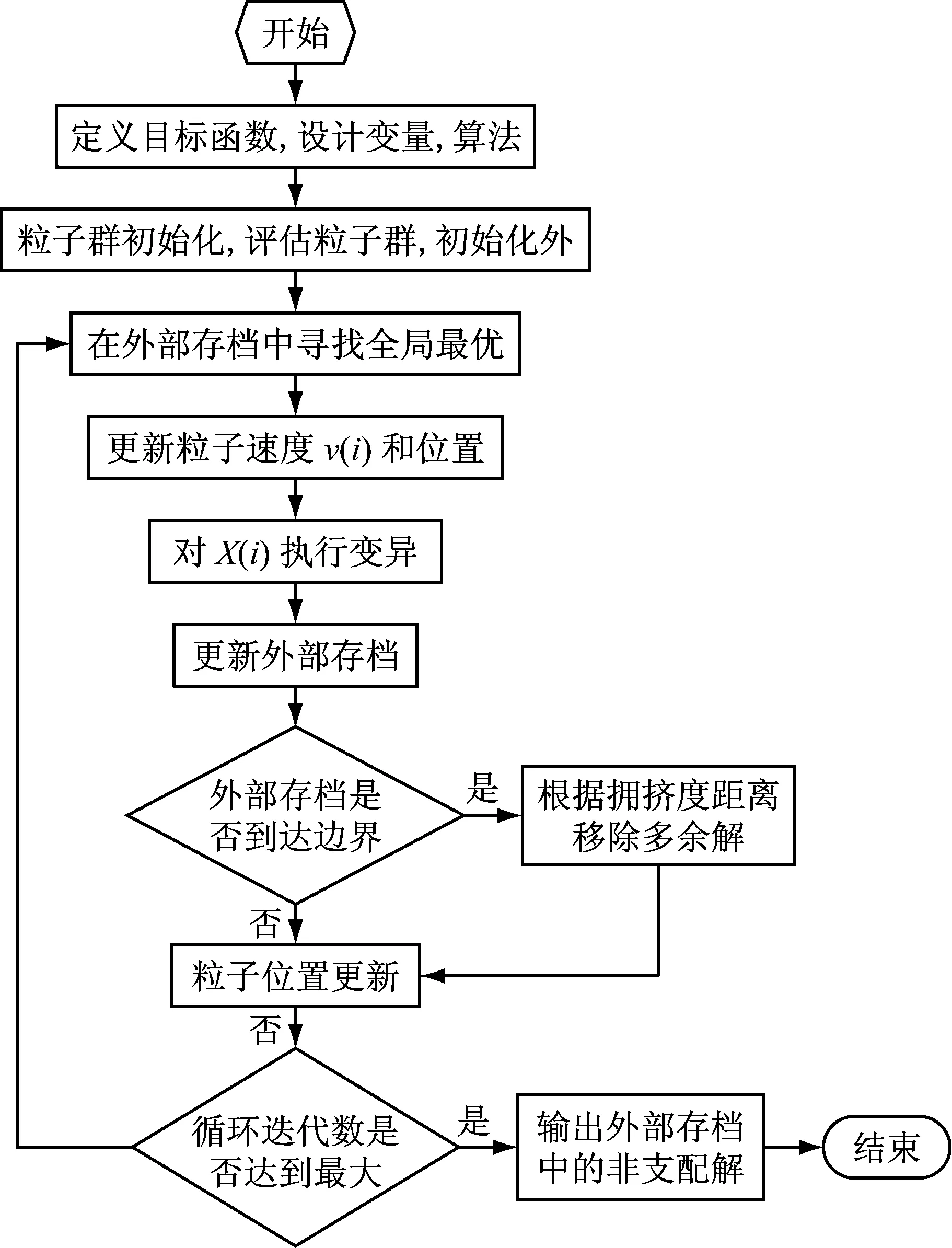
图11 算法流程图
3.2 多目标优化
基于改进的多目标粒子群算法(MDPL-MOPSO),对图1中12自由度振动力学模型进行多目标优化。
(1) 设计变量
设计变量定义为X=[x1,x2,x3,x4] =[K3,K4,C3,C4] 。
(2) 两目标函数
每一组两目标的帕累托优化前端如图12(篇幅限制只列出40 km/h在B级路面的多目标优化的仿真结果)。从图中可以看出,一个目标的改善,造成另一个目标性能变差。图12(a) 是驾驶室地板垂直加速度和前轮动载优化帕累托前端。图中A1点是驾驶室地板加速度最小点,B1点是前轮动载最小点。设计人员可以选择其中一个折中点作为设计优化解,如图中的C1点。其它几组两目标优化的帕累托前端如图12(b)~图12(d) 。
(3) 多目标优化
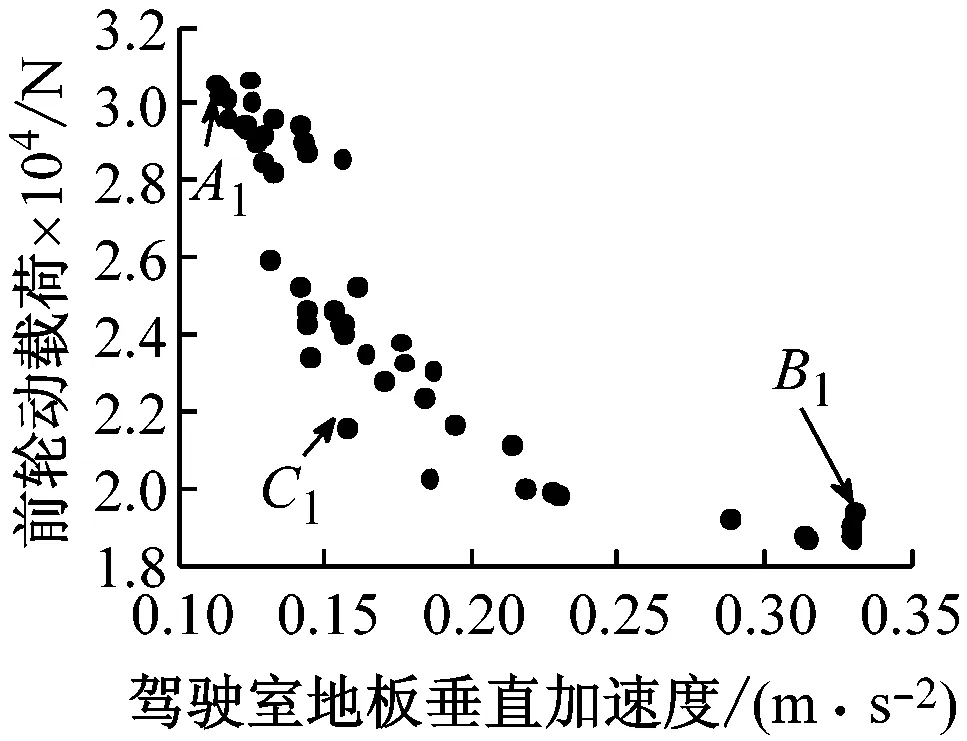
(a) 驾驶室地板加速度和前轮动载帕累托前端
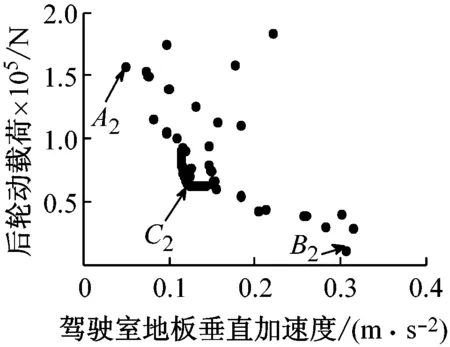
(b) 驾驶室地板加速度和后轮动载帕累托前端
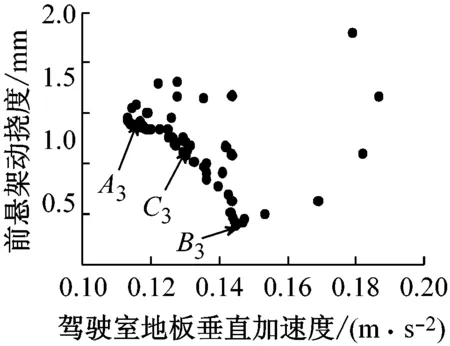
(c) 驾驶室地板加速度和前悬架动挠度帕累托前端
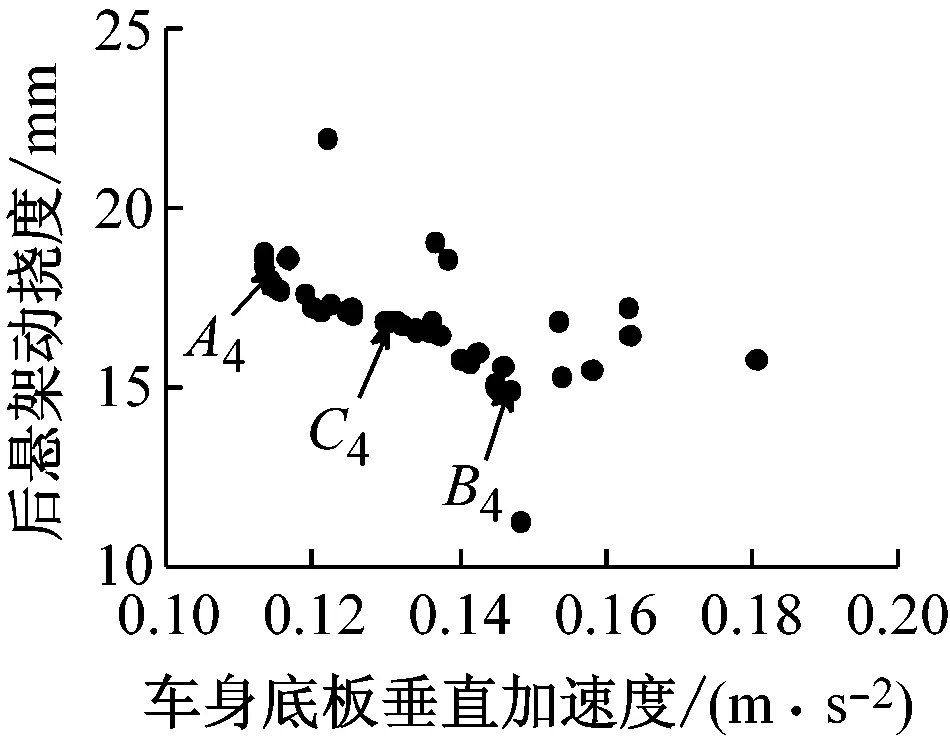
(d) 驾驶室地板加速度和后悬架动挠度帕累托前端
图12 两目标函数优化帕累托前端
Fig.12 Pareto front end of two objective functions optimize
图13为三目标的优化结果。与两目标优化结果比较具有相同的性质,即一个目标的改善,造成另两个个目标性能变差,而优化效果更好。从图13(a)可看出,随着驾驶室地板加速度的改善,前轮动载加大,后轮动载则变化不大。图13(b)显示,随着驾驶室地板加速度的改善,前悬架动挠度加大,后悬架动挠度则变化不大。同样可以选出一组折中的帕累托优化解,见图13中的P1和P2点。
表4是优化前后悬架参数的对比,针对不同的目标函数,优化后的悬架参数不同,设计人员可以根据具体的设计目标做出选择。图14为优化前后驾驶室地板加速度频域分析结果对比,在选择的两组帕累托优化设计参数,其驾驶室地板加速度都有明显的改善,加速度均方根值降幅达到30%,达到了平顺性的优化目的,其他目标都有不同程度的改善。

表4 优化前后悬架参数结果对比
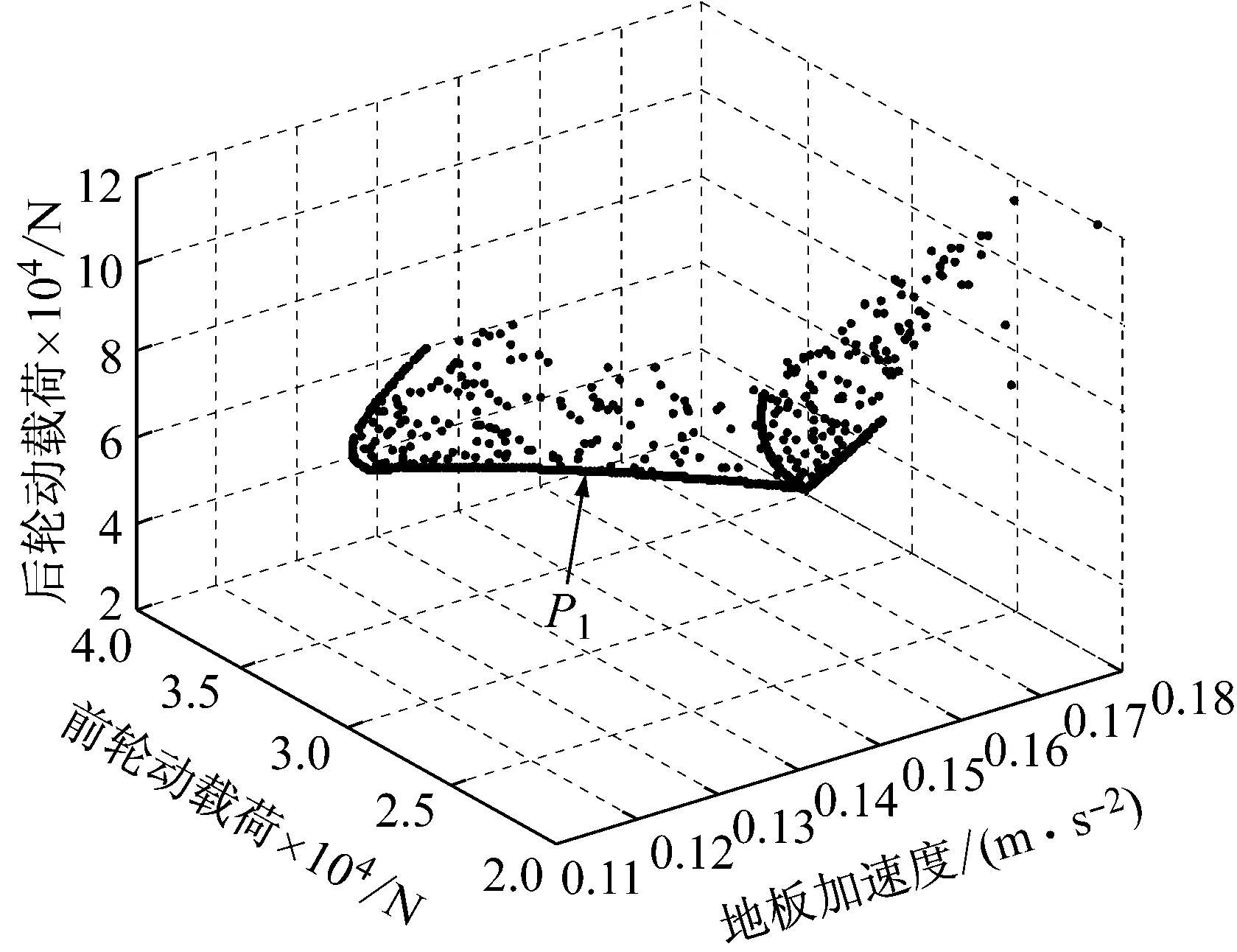
(a) 驾驶室地板加速度、前轮动载和后轮动载帕累托前端
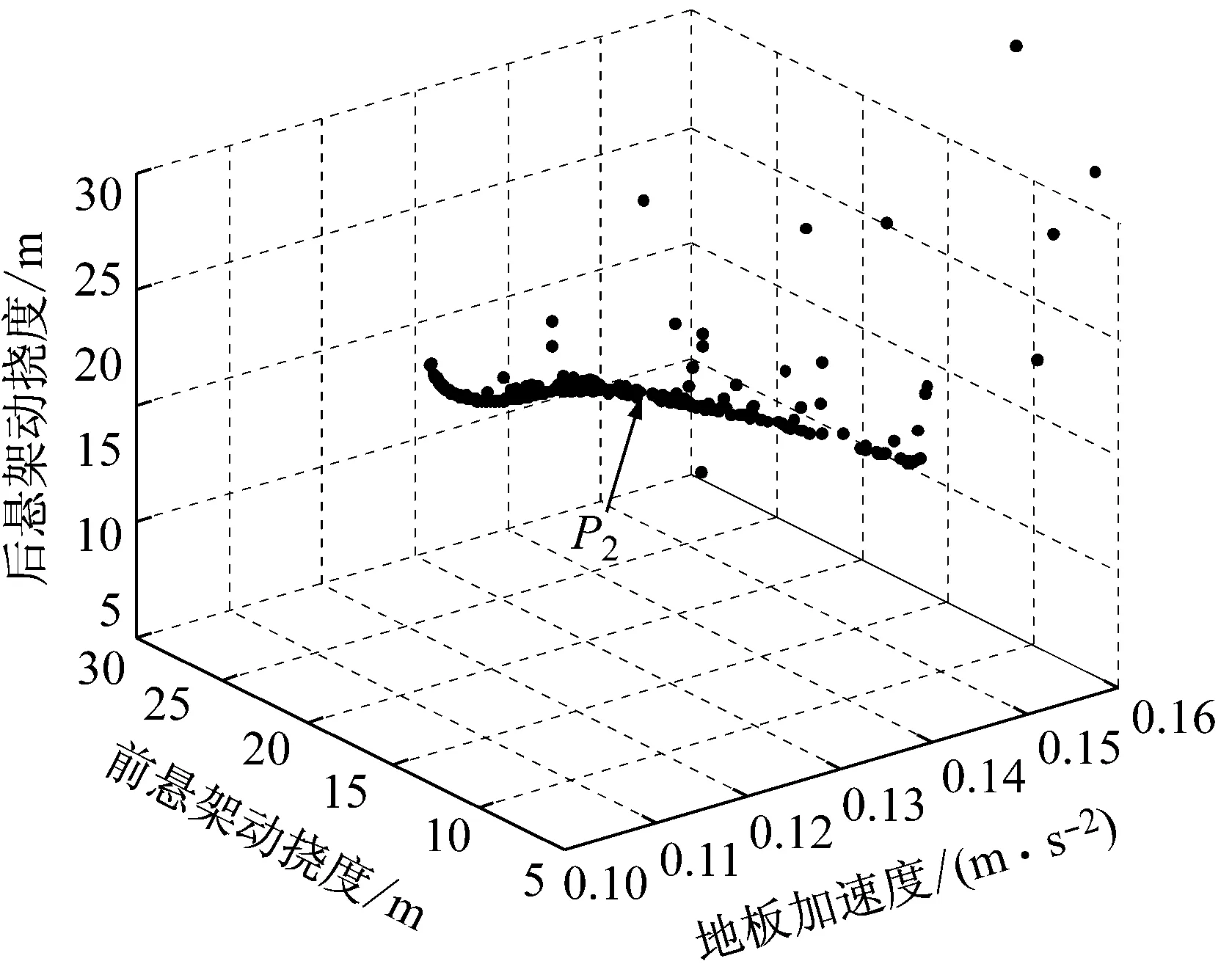
(b) 地板加速度、前悬架动挠度和后悬架动挠度帕累托前端
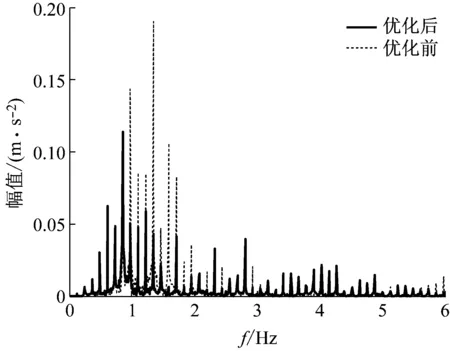
(a) P1点优化前后驾驶室地板加速度频域对比
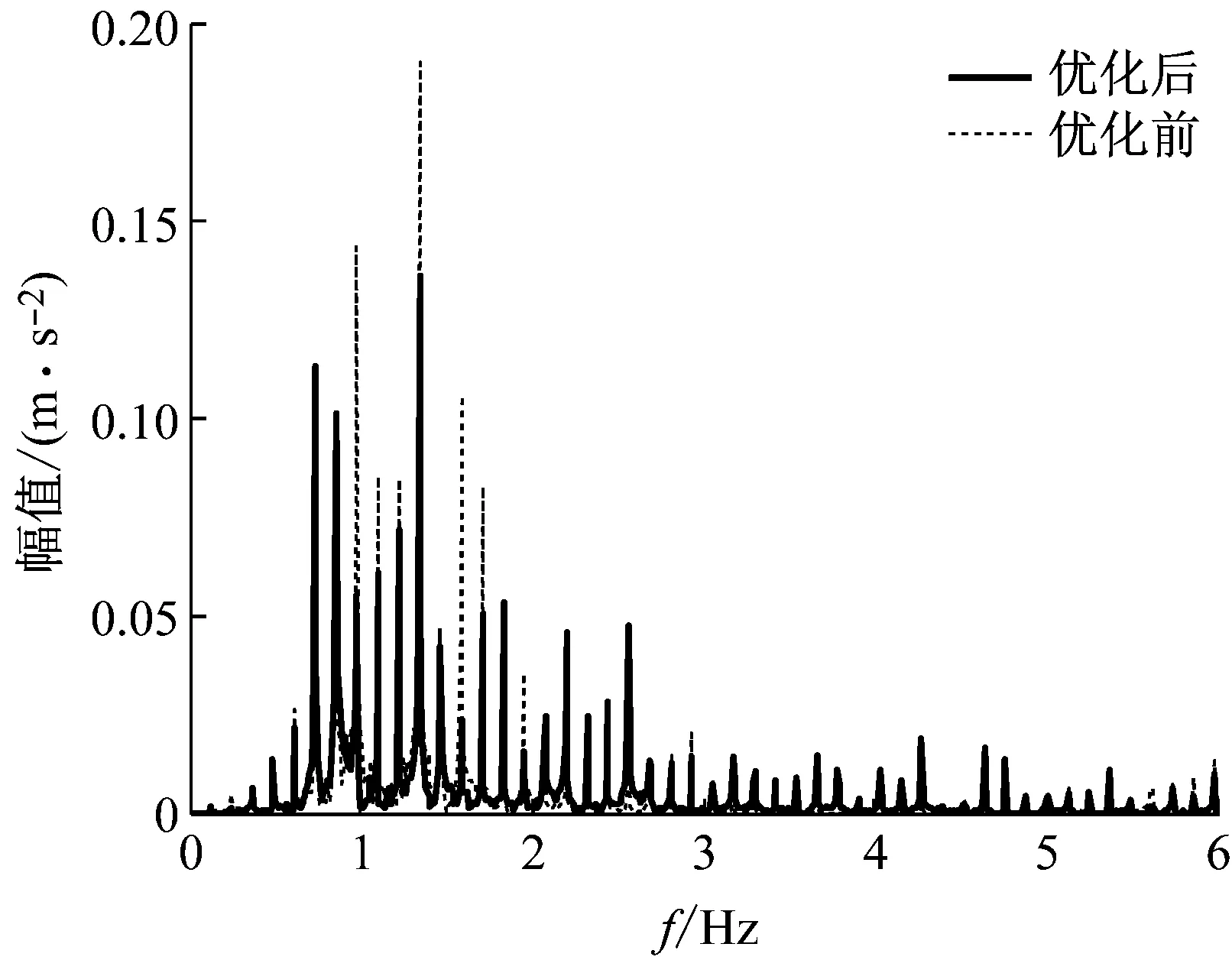
(b) P2点优化前后驾驶室地板加速度频域对比
4 结 论
(1) 建立了某6×4牵引车列车12自由度振动力学模型,并对仿真运算结果和试验结果进行对比分析,验证了模型的精度满足设计要求。
(2) 提出一种改进的多目标粒子群优化算法,点到直线最小距离的改进多目标粒子群优化算法 (MDPL-MOPSO) ,改进寻找粒子全局最优指导的方法,提升算法的收敛性和多样性。