低幅值应力波在岩石三维节理面的折反射规律理论研究
2018-08-27刘传正张建经
刘传正, 张建经, 崔 鹏
(1.中国科学院 山地灾害与地表过程重点实验室 成都山地灾害与环境研究所,成都 610041;2.中国科学院大学 工程科学学院,北京 100049;3.西南交通大学 土木工程学院,成都 610031)
岩体中的结构面很大程度上影响了岩体的力学性质。近些年来,由于地震事故频发,并引发了大量的崩塌、滑坡灾害,地震作用下岩土体失稳机理成为当前十分迫切的研究任务之一。而岩石节理对应力波传播的影响规律对于研究地震岩质边坡动力响应与失稳机理具有重要意义。
岩石节理力学性质的研究始终贯穿于岩石力学中的研究中,是岩石工程常常所面对的不可忽视的客观存在。岩石节理力学研究早期是对二维粗糙节理力学进行研究,而对于三维粗糙节理的研究则相对较为有限,但是仍有大量的研究发现,如Belem等[1]通过对节理面几何统计分析发现,对于自然形成节理,岩石节理面凸起的倾角和曲率以及节理的粗糙度与曲折度,都会表现出一定的各向异性性质。孙辅庭等[2]运用分形数学理论,提出了一种基于三维均方根抵抗角的节理面粗糙度分析方法,分形参数在方位角上表现出明显的各向异性性质。Jing等[3]通过岩石节理面剪切实验发现,在各方向上节理起伏角并不是均匀分布的,且节理的剪切变形刚度系数在各个方向上也不相等;进一步研究发现岩石节理起伏角的各向分布与剪切刚度在方向上分布呈正相关,且具有中心对称的两个优势方向,可用椭圆描述。Jing等[4]在岩石节理表面形态各向异性研究的基础上,给出了岩石节理三维本构模型。类似的,王光纶等[5]给出了具有非线性弹性变形的岩石节理三维本构方程。而Misra[6]则基于三维弹塑性接触理论、节理面形态的几何参数分布函数给出了积分形式的岩石节理三维本构力学模型。以上研究均表明中皆从岩石三维节理面的形态作为主要出发点,有些给出三维节理本构方程,然后都过去研究中可以发现三维节理变形本构方程的刚度矩阵中交叉耦合项非零;由于节理变形方程中交叉耦合刚度系数是描述岩石节理力学性质重要参数,如描述了节理的剪胀、减缩现象,而且节理本构方程中交叉耦合刚度系数不仅仅描述这两种现象,其对应力波在节理上折反射规律的影响相关研究也十分缺乏。
相比岩石节理力学性质的研究,过去在研究岩石节理应力波传播规律中对节理本构模型则做出了较大简化,其很大原因是由于问题求解的复杂性。Schoenberg[7]基于位移非连续模型,给出应力波在线刚度非连续面上的折反射解析解,随后很多学者对此方法进行了研究和补充,如Myer等[8-15]通过理论、实验对线刚度DDM(Displacement Discontinue Method)模型进行大量研究,证明了该理论的可靠性和实用性。Zhao等[16]给出了纵波垂直入射非线性变形节理面的解析解;俞缙等[17-18]对非线性节理面的应力波传播模型进行了改进。Daehnke等[19]给出考虑交叉耦合项的二维节理面DDM模型解析解。Misra等[20]在给出的三维节理本构模型的基础上,分析了应力波的折反射行为,但是其理论框架仍是在传统的认识范围内。综上述,以往研究没有对三维粗糙节理的应力波折反射行为进行探讨,没有全面的分析三维节理本构方程中的交叉耦合刚度系数项对三种简谐波传播的影响。
本文基于岩石节理的细观接触模型,讨论了岩石节理一般形式的三维应力-应变本构方程,并以此为基础分析了简谐波在节理面上的相互转化机理,并据此推导了三维节理上应力波折反射的理论解,最后重点讨论了节理本构方程中的交叉耦合项对应力波折反射系数的影响。
1 岩石节理的形变刚度讨论
1.1 三维粗糙节理接触变形机理
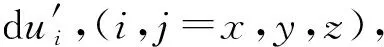
(1)
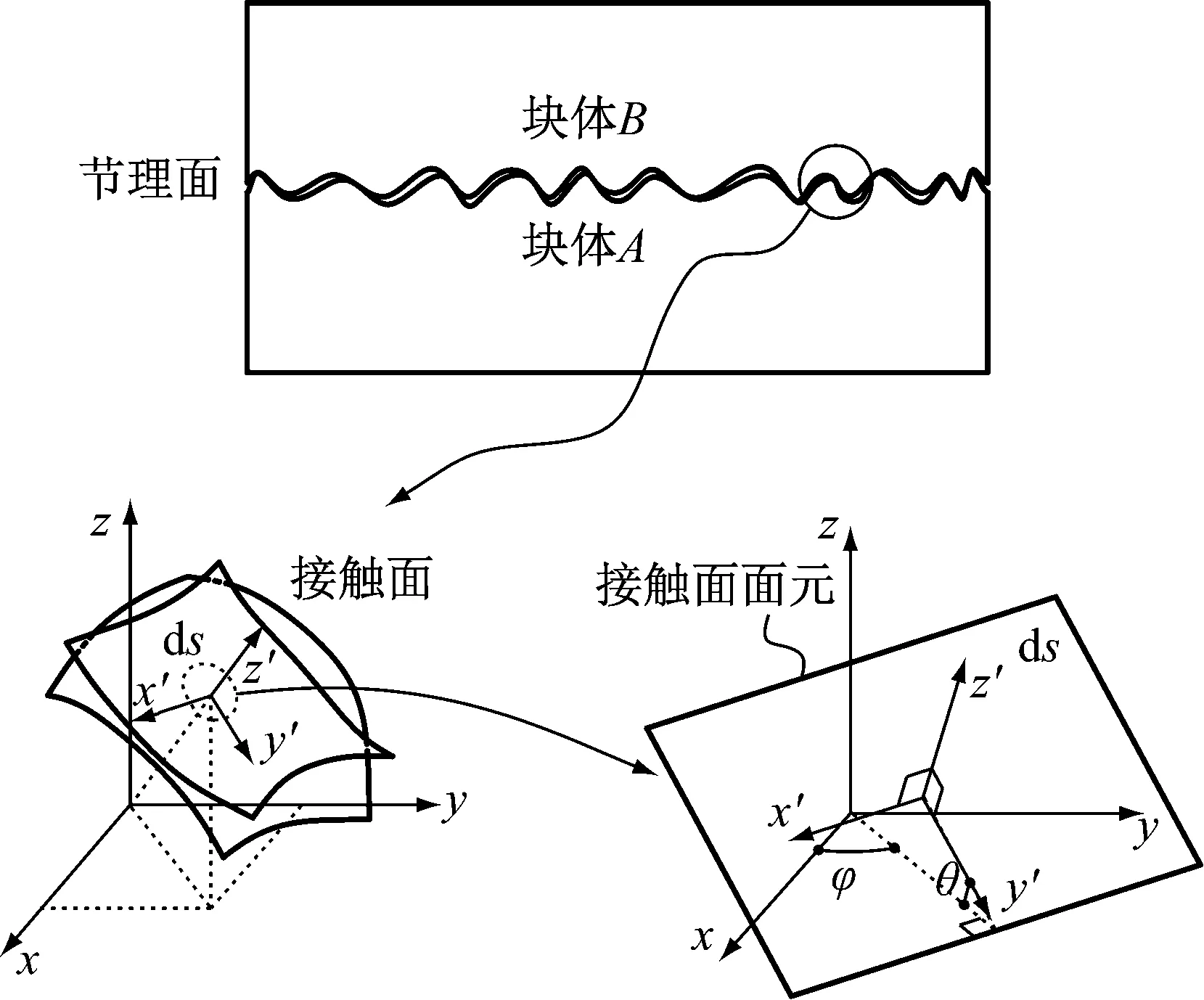
图1 节理凸起接触示意图
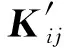
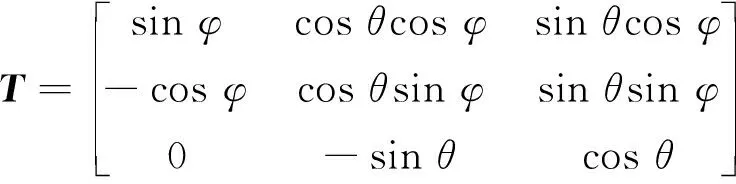
(2)
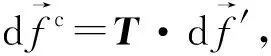
(3)
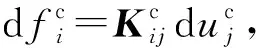
(4)
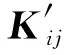
1.2 三维节理的本构方程
由接触面的本构方程,即可以得出节理的整体本构方程,但是需知节理上接触点在空间的分布情况。如图2所示,设节理单位面积内的接触点的分布密度为ρc(与节理上下壁面形态、应力水平有关),而接触点在高程上的分布密度函数为H(z),则ρcH(z)dz则是指单位面积节理上的高程z~z+dz的所有接触点数目。由此可以得出,此时单位面积节理上接触点的数目为
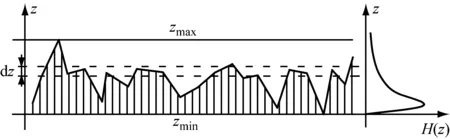
图2 节理表面高程分布
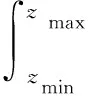
(5)
而对于节理上接触点的分布,应根据具体的情况选用适当的分布函数来描述,例如:卡方分布χ2、伽马分布Γ(α,β),F分布等。
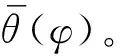
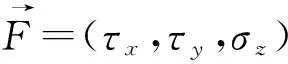
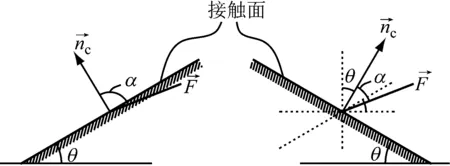
图3 接触面与作用力
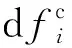
(6)
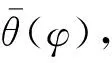
(7)
式中:Δz=[zmin,zmax]。将节理凸起的接触变形方程式(3)代入式(7),得
(8)
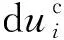
(9)
这里刚度系数Kij为此时节理变形的刚度系数。由式(9)可以看出节理的变形刚度系数Kij与节理的形态特征、应力状态密切关。由于在岩石节理的变形过程中,节理上下两壁之间的接触面的分布、形态等是动态变化的,因此变形刚度矩阵Kij是动态变化的。三维节理的变形刚度矩阵为3×3的矩阵,非对角线上的刚度系数一般非零-由式(9)可知,在节理为平直节理时,非对角线上的刚度系数为零;或者对于倾角在倾向上为对称分布,且当节理当前应力状态为0时,或仅法向应力存在时节理变形矩阵中的非对角线上的刚度系数为零;对于其他情形,需要根据节理面的形态进行具体的分析。然而,这里并不给直接给出节理本构方程的具体形式,且对于动力问题,应力波在三维非线性本构节理上折反射求解异常复杂,不利于理论解析。然而对于低幅值应力波入射时,应力波动幅值相对节理的强度较小时,可以认为此时节理的变形为线刚度模型,因此这里对岩石节理本构方程为三维线刚度模型时的应力波折反射规律进行分析。
2 三维节理的应力波折反射理论分析
令节理的平均面为XOZ坐标平面,法向为Y轴;设应力波入射线所在平面为XOY平面,则P波、SV波的偏振方向在XOY平面内,而SH波的偏振方向为Z轴方向。节理上下两壁岩石块体A,B为线弹性介质。由前面的讨论可知,当低幅值应力波入射时,节理本构方程可以采用的三维线刚度本构方程dFi=Kijduj来表示。由线性问题的可叠加性可知,此时在应力波入射与折、反射过程中,节理本构方程可以改写为
(10)
式中:[δσy,δτyx,δτyz]T为节理上的应力变化分量,Pa;[δuy,δux,δuz]T为节理上下壁面的相对位移变化分量,m;kij,i,j=x,y,z为节理的变形刚度系数,Pa/m。且在本文中将处于矩阵K对角线上的kxx,kyy,kzz称为主刚度系数,而位于对角线之外刚度系数称为交叉耦合刚度系数。根据热力学第二定律可以证明,节理刚度系数矩阵Kij必为实对称阵,即kij=kji。由波动理论可知,沿同一方向传播的应力波,P波、SV波与SH波之间的偏振方向是相互正交的,如图4所示当P波垂直入射时,节理面会产生扰动δuy,δσy;SV波垂直入射时,会产生扰动δux,δτxy;而P波、SV波倾斜入射时,都会在节理面产生扰动δuy,δσy和δux,δτxy。而SH波无论是垂直入射还是倾斜入射仅会产生扰动δuz,δτyz。垂直方向的扰动δuy,δσy会因为节理刚度系数kyy产生垂直方向的变形和应力反馈δuy,δσy;再由波动原理可知,一个平面上无数质点作为振源辐射出垂直扰动会形成平面波阵面,从而形成反射和透射的P波。类似的原理,垂直扰动δuy,δσy会因节理刚度系数kxy反射和透射SV波,因刚度系数kyz反射和透射SH波。同理,剪切扰动δux,δτxy和δuz,δτyz也能够分别产生P波、SV波与SH波。
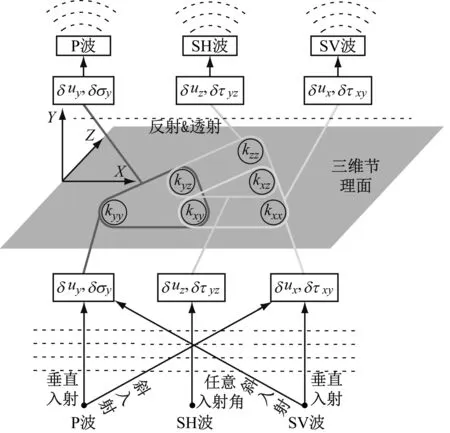
图4 应力波在三维节理上转化机理示意图
Fig.4 Mutual transformation mechanism of stress wave on 3D rock joint
因此对三维岩石节理,当交叉耦合刚度系数不为零时,如图5所示,P波、SV波或SH波会因刚度系数kxy,kyz,kxy而能够相互转化。
这里采用DDM(位移不连续方法)来研究应力波折反射问题,且节理的变形本构方程式(10)与应力连续条件作为求解的边界条件,入射波、反射波与透射波的波动方程与符号约定如表1所示。
节理的变形[δuy,δux,δuz]T可以表示为
(11)
式中:[δuAy,δuAx,δuAz]T为岩石块体A上节理的位移
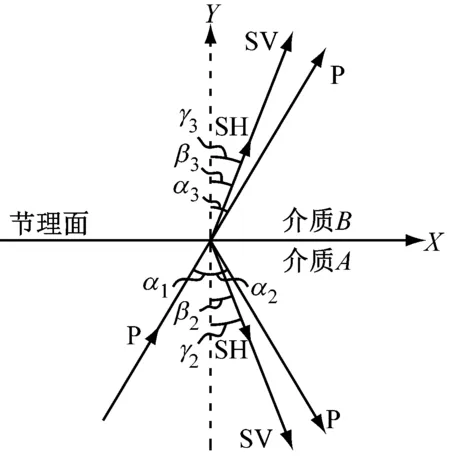
(a) P波入射
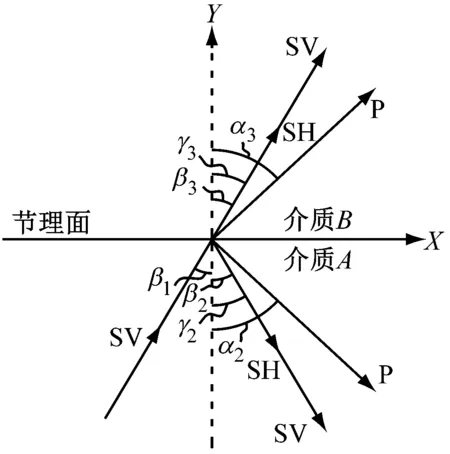
(b) SV波入射
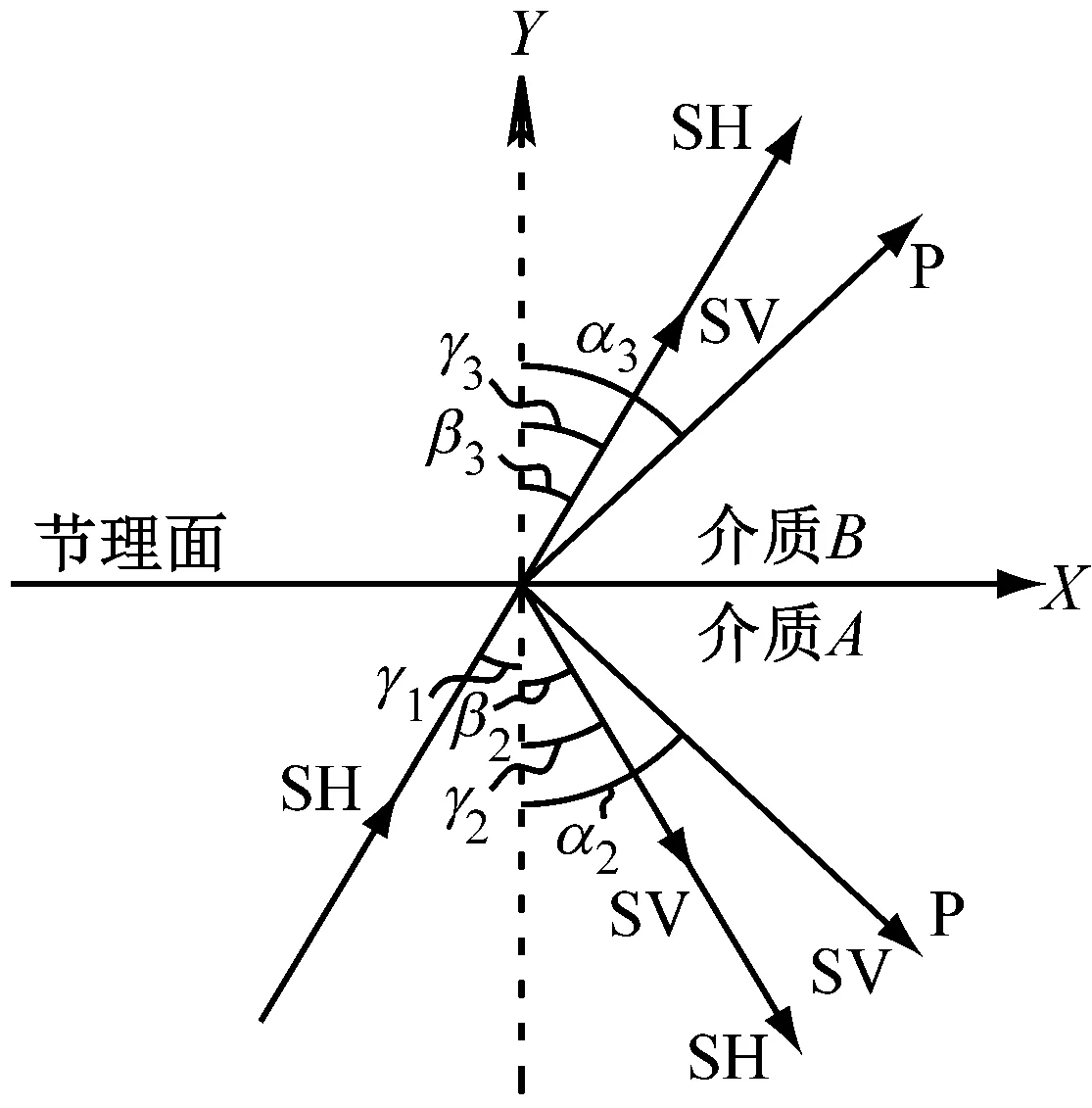
(c) SH波入射
变化量;[δuBy,δuBx,δuBz]T为岩石块体B上节理的位移变化量。而由应力波的传播方向和质点的偏振方向,可以得出岩石块体A与块体B的位移分量为
(12)
(13)
再由几何变形方程,可以得出块体A与块体B中的应变分量εAij与εBij。使用广义胡克定律,即可以得出块体A、块体B中的应力分量σAij与σBij。由DDM模型的假设:节理面上的应力连续条件σAij|y=0=σBij|y=0和变形方程式(10),并令应力波的反射系数与透射系数为未知量,可以得出求解方程
X·E·C=ein·B
(14)
式中:X为求解方程的系数矩阵,与节理变形本构方程和入射波的频率、角度有关,具体形式为
(15)
式中:λA,μA为岩石块体A的拉梅常数;λB,μB为岩石块体B的拉梅常数。E为指数矩阵
(16)
式中:C为反射应力波与透射应力波的幅值系数,具体形式与入射应力波的类型有关,当入射波为P波时,C为
(17)
式中:简写为C=[RP→P,RP→SV,RP→SH,TP→P,TP→SV,TP→SH]T,类似的当入射波为SV波时,折反射系数可以写为C=[RSV→P,RSV→SV,RSV→SH,TSV→P,TSV→SV,TSV→SH]T;当入射波SH波时,折反射系数可以写为C=[RSH→P,RSH→SV,RSH→SH,TSH→P,TSH→SV,TSH→SH]T。

表1 波动方程与符号约定
ein·B为式(14)的非齐次项,具体形式与入射波类型有关,当入射波为P波时,ein·B可以写为
einBP=eiκAd(xsin α1-CAdt)×
(18)
当入射波为SV波时
(19)
当入射波为SH波时
(20)
由稳态应力波场可知,应力波在非连续面上传播时应该满足Snell定律。对于三维节理面而言,Snell定律这里可以表示为
ω=κAdCAd=κAsCAs=κBdCBd=κBsCBs
(21)
因此,由以上分析和推导可知,对于三维粗糙节理面,由于刚度系数矩阵中交叉耦合项存在,简谐P波、SV波与SH波同时相互作用,之间能够发生能量相互转换,且SV波与SH波具有相同的反射角β2=γ2与透射角β3=γ3。将式(21)代入式(14),即可以求出节理上的折反射系数C。
3 三维节理应力波折反射规律分析
三维岩石节理对应力波传播的影响,与以往研究相比最大的不同点在于:三种类型的简谐波在节理上可以相互转化,且本构方程中刚度矩阵中交叉耦合项起到重要的作用。基于上节给出的应力波在三维粗糙节理折反射的理论解,这里针对交叉耦合刚度系数对节理折反射应力波的幅值系数影响进行分析。
3.1 入射角对应力波折反射系数的影响
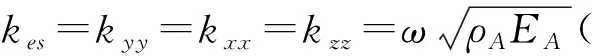
图6为P波入射时,折反射系数RP→P,TP→P,RP→SV,TP→SV,RP→SH和TP→SH随入射角α1的变化规律。应力波的幅值系数随入射角的变化曲线与过去DDM(无交叉耦合刚度项)所得的幅值系数类似,但是交叉耦合刚度系数的存在使得曲线有所变化,随着节理中交叉耦合项的增大,与入射波同型的反射波的反射系数RP→P增大,且与入射波同型的透射波的幅值系数TP→P减小。若无交叉耦合刚度系数存在,则不会生成转换波SH波;对于转换波SV波,交叉耦合刚度系数的存在一定程度上改变了SV波折反射系数RP→SV,TP→SV的变化规律。但是总体上来说,随着交叉耦合刚度系数的增加,转换波的幅值系数是增大的。类似的规律在SV波入射时同样成立,见图7所示。SH波入射时,若无交叉耦合刚度系数存在,则转换波P波与SV波则不会产生,如图8所示;随着交叉耦合刚度系数的增大,同型波反射系数RSH→SH增大,同型波透射系数TSH→SH减小,且转换波折反射系数增大。
3.2 节理刚度系数对应力折反射系数的影响
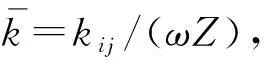
如图9所示,P波垂直入射仅会导致节理面上的质点在y轴方向运动,因此刚度系数kzx对应力波传播没有影响,见图9(c)。随着刚度系数kxy的增大,与入射波同型波的反射系数RP→P和转换SV波RP→SV,TP→SV的增大,与入射波同型波的透射系数TP→P减小,此时没有SH波产生,见图9(a)。类似的,当变量为刚度系数kyz时,同型波的反射系数RP→P和转换SH波RP→SH,TP→SH随着kyz的增大而增加,同型入射波TP→P减小,且没有SV波形成,见图9(b)。相似的规律在SV波与SH波垂直入射时同样存在,见图10与图11,这里不再赘述。
4 结 论
本文在讨论三维岩石节理本构方程的基础上,通过合理的简化,分析了平面谐波在节理面上的作用机理,并给出了平面谐波在三维节理上的折反射理论解。并通过参数分析初步探讨了P波、SV波和SH波入射时,反射波与透射波的幅值系数随入射角以及交叉耦合刚度系数的变化规律。本研究得出以下有意义结论:
(1) 简谐波P波,SV波或SH波在三维节理上可以相互转化,由于节理的交叉耦合变形刚度系数的存在,使得P波、SV波与SH波在节理面上可以发生波动能量的相互传递和转化。
(2) 三维粗糙节理本构方程中的交叉耦合刚度系数越大,则越多的入射波能量转化为转换波能量;且同型反射波幅值随交叉耦合刚度系数增大而增大,同型透射波幅值随之减小。
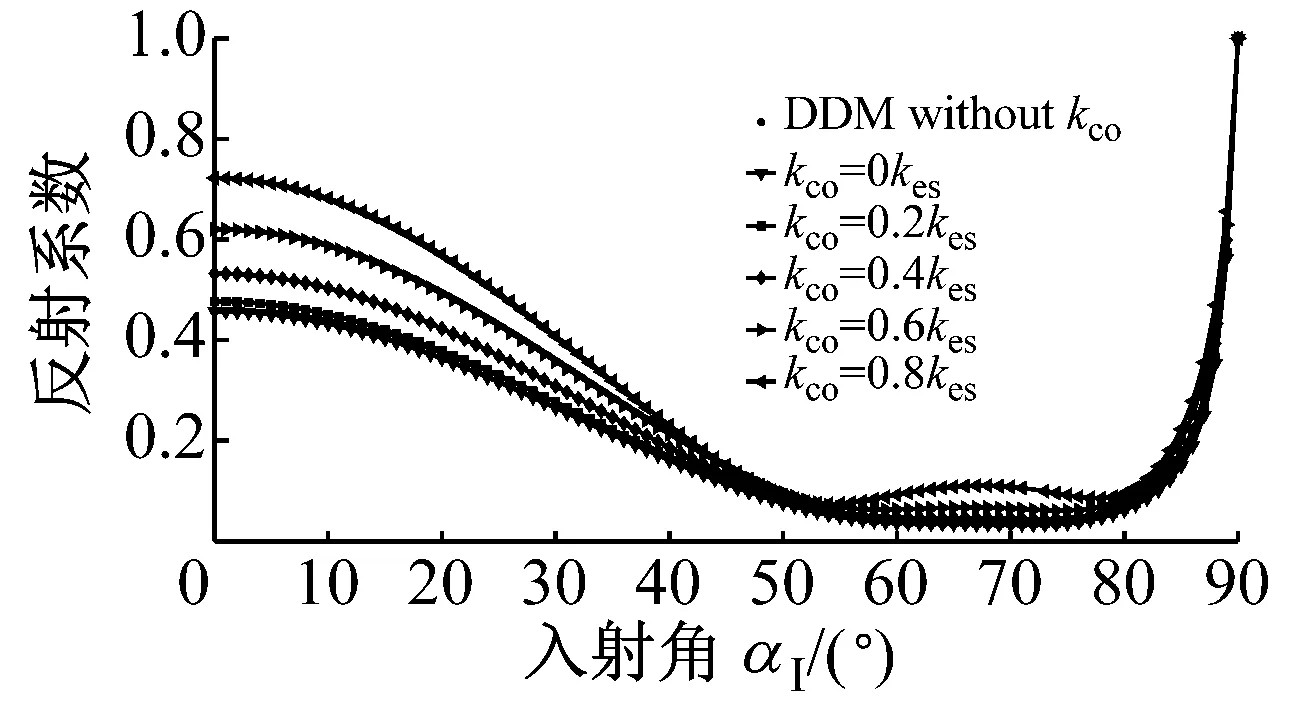
(a) RP→P
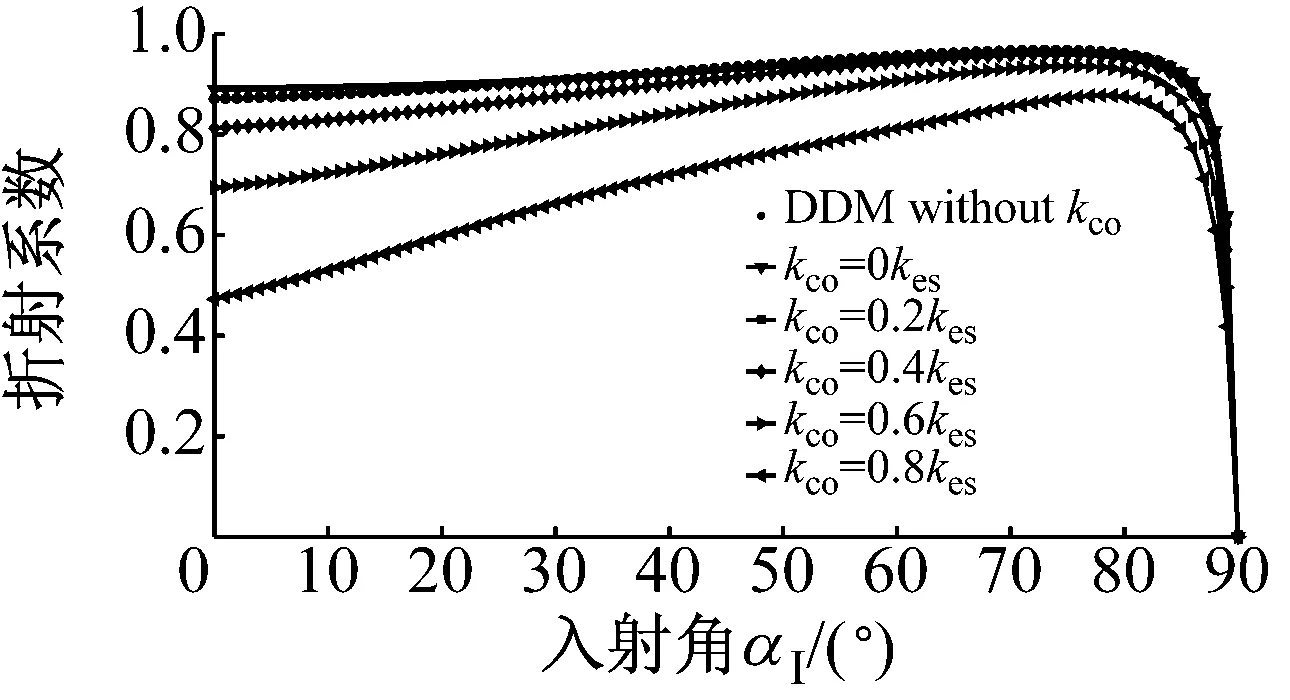
(b) TP→P
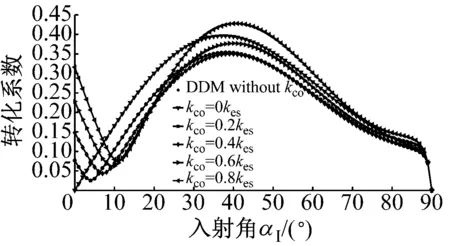
(c) RP→SV
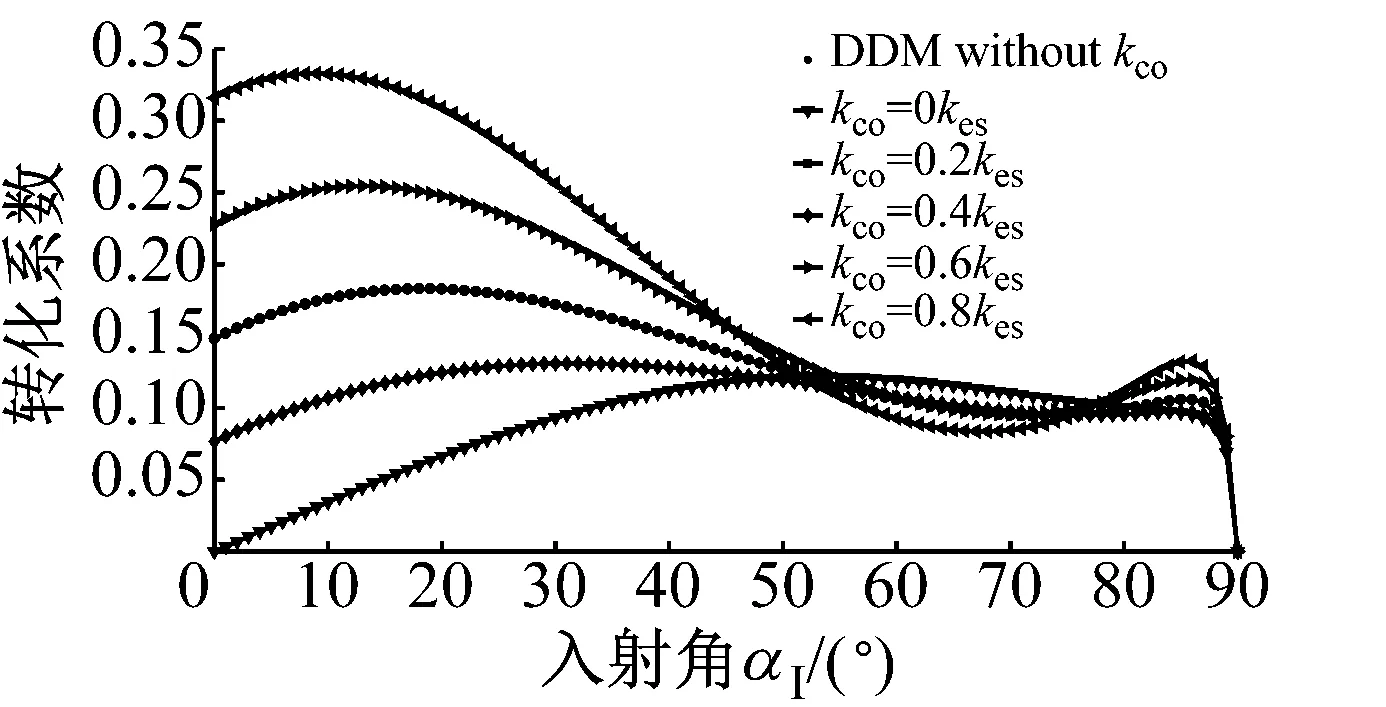
(d) TP→SV
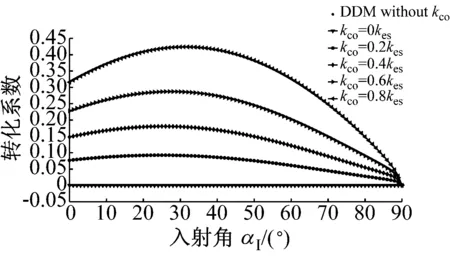
(e) RP→SH,TP→SH
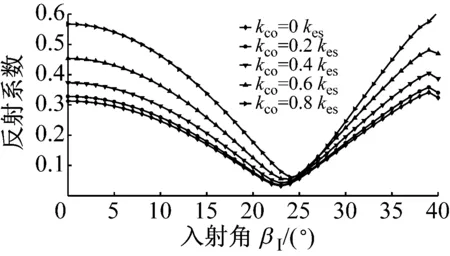
(a) RSV→SV
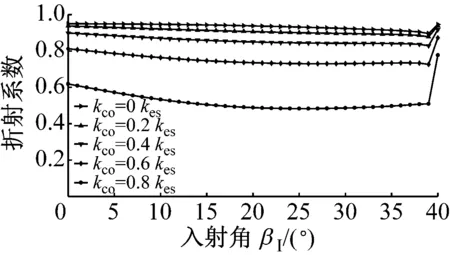
(b) TSV→SV
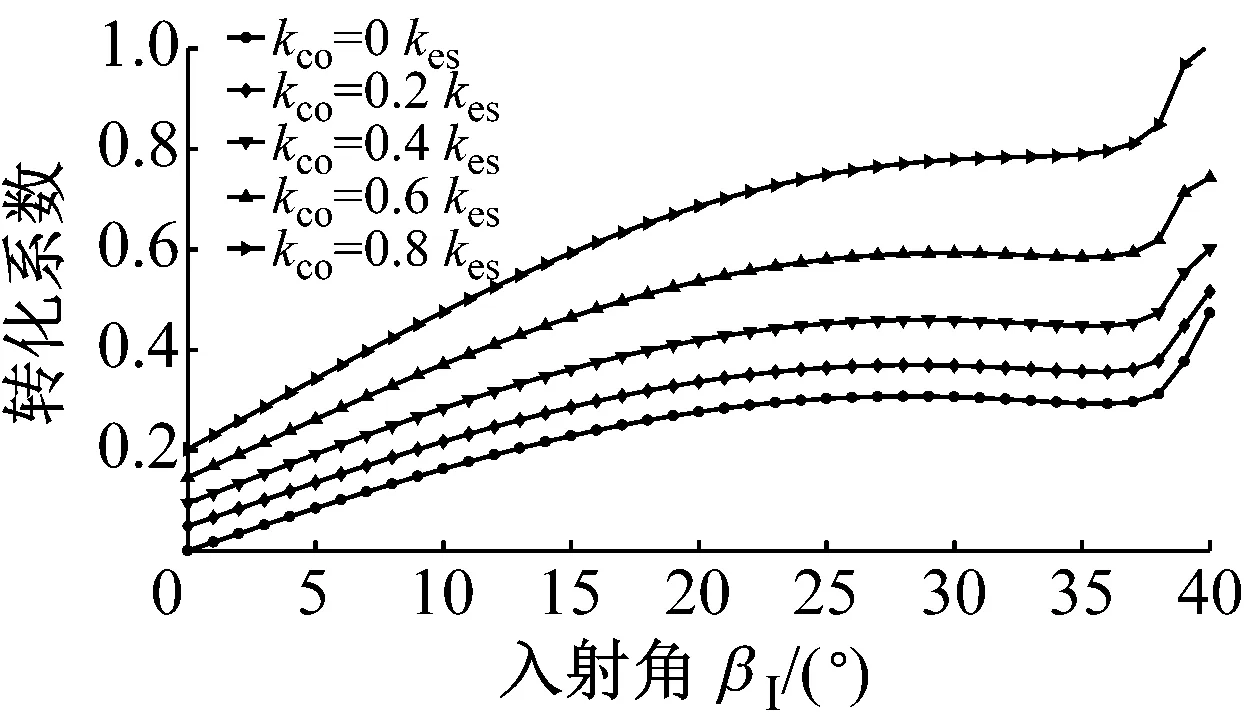
(c) RSV→P
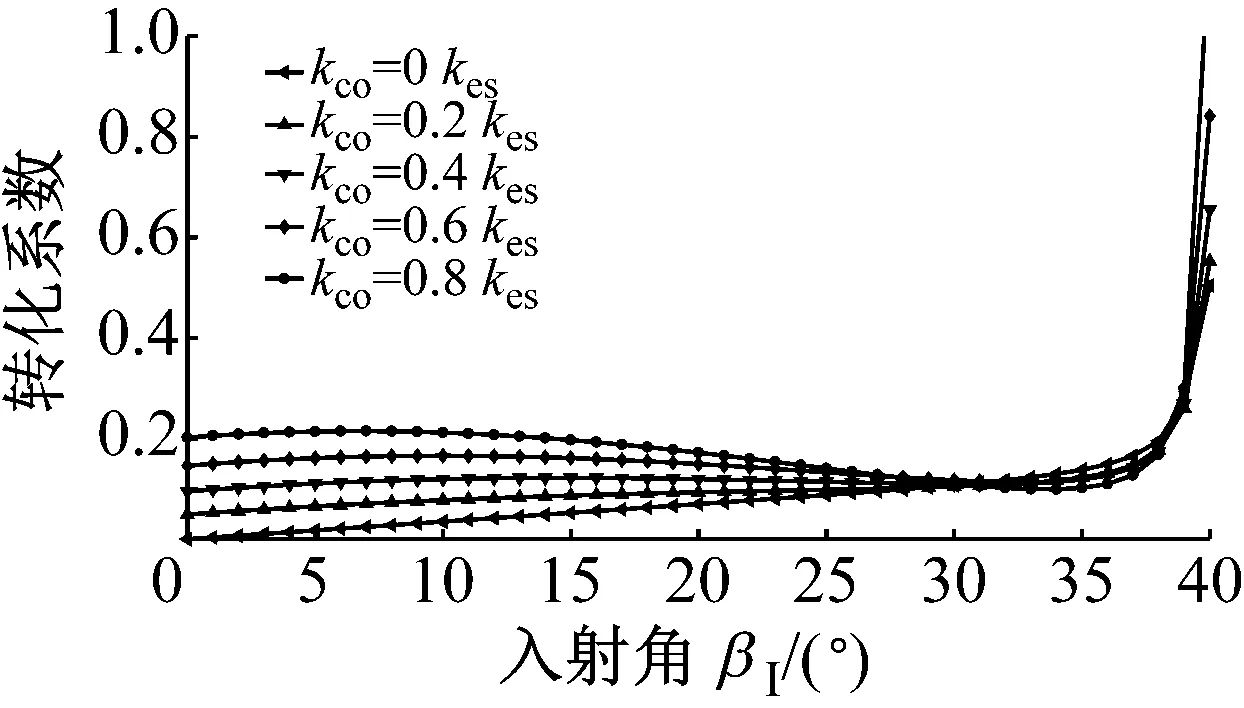
(d) TSV→P
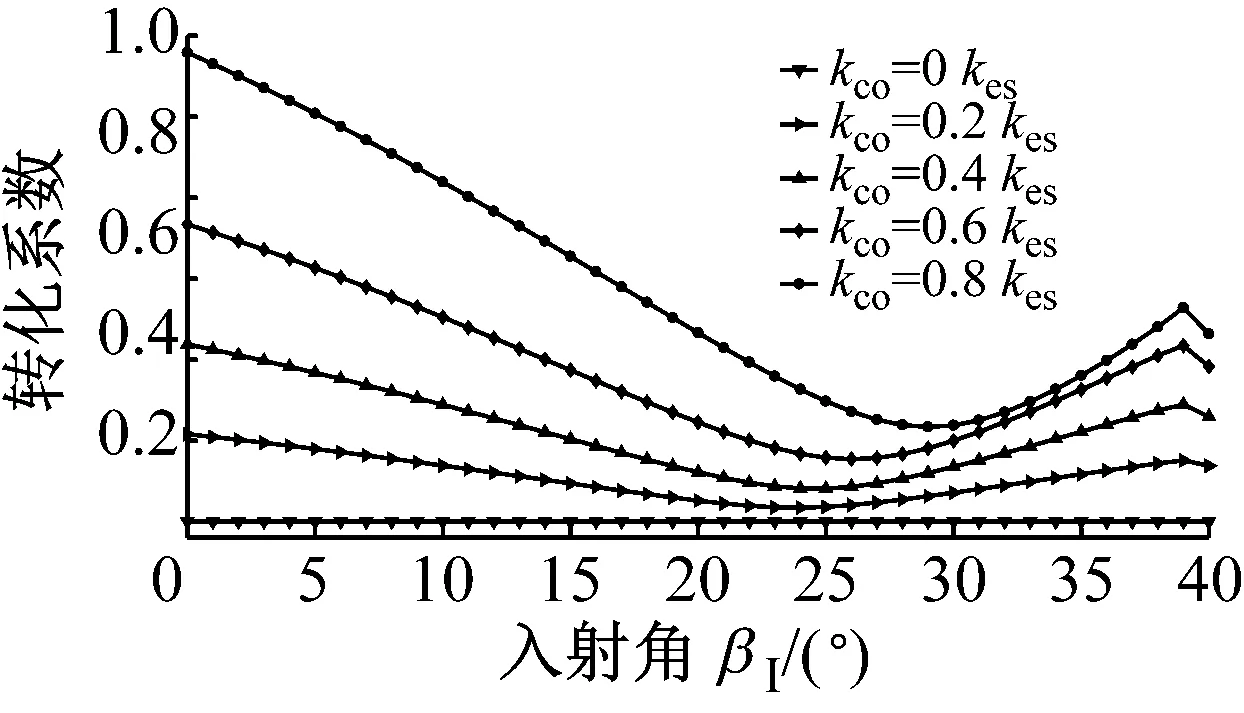
(e) RSV→SH,TSV→SH
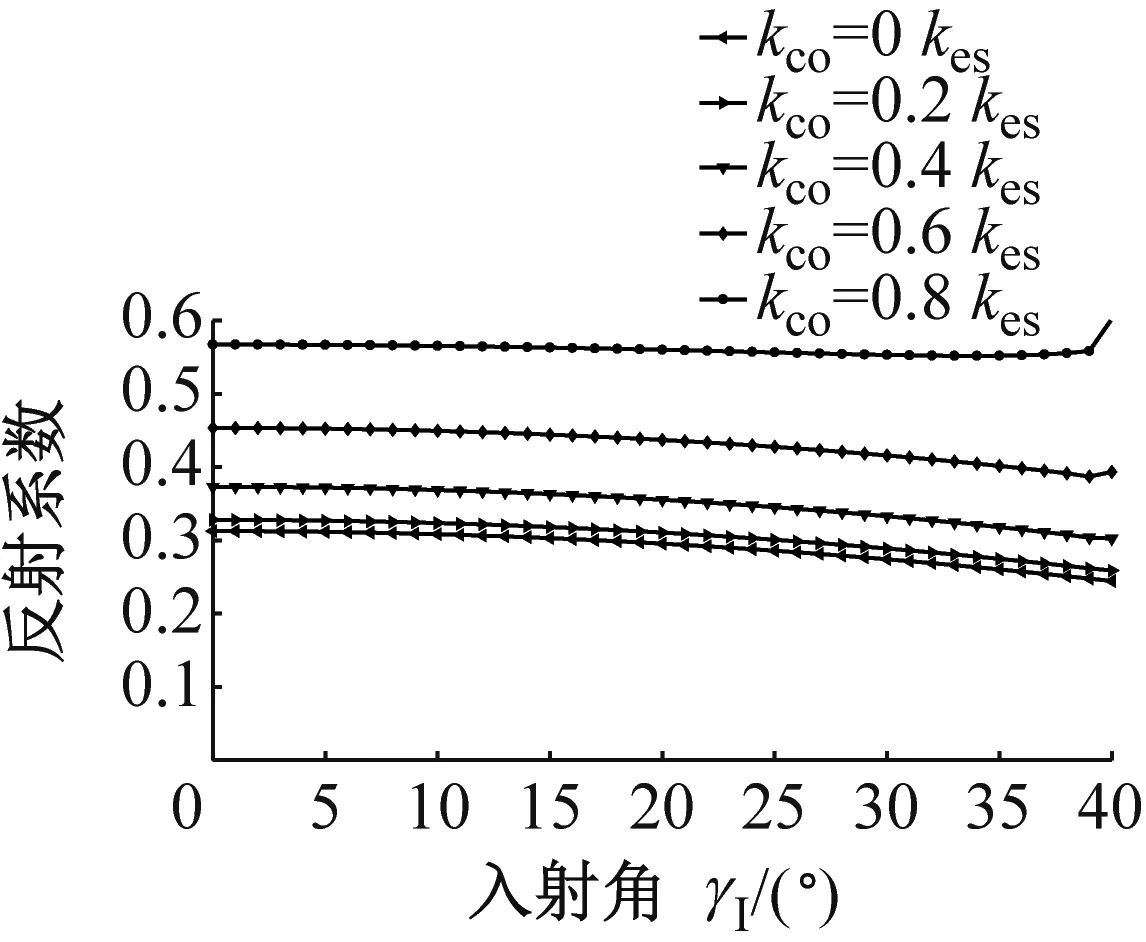
(a) RSH→SH
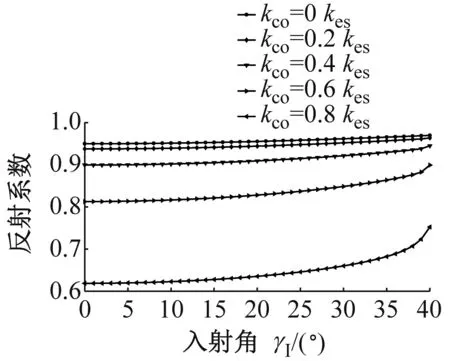
(b) TSH→SH
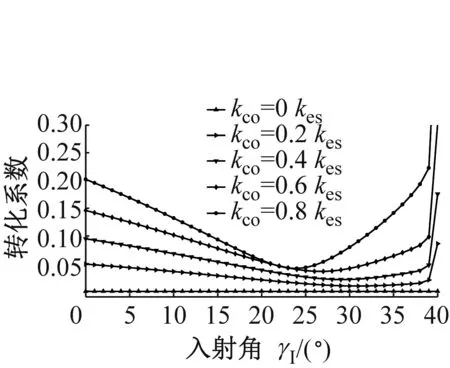
(c) RSH→P
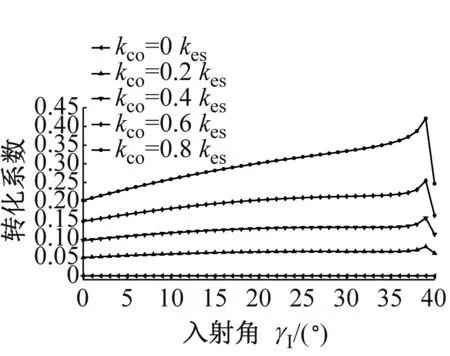
(d) TSH→P
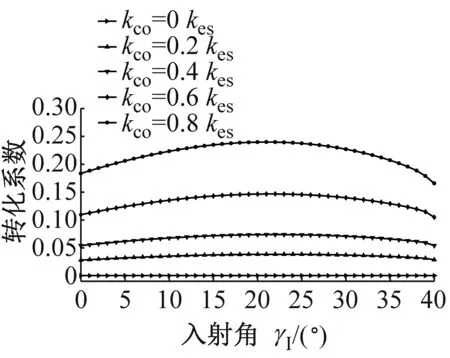
(e) RSH→SV
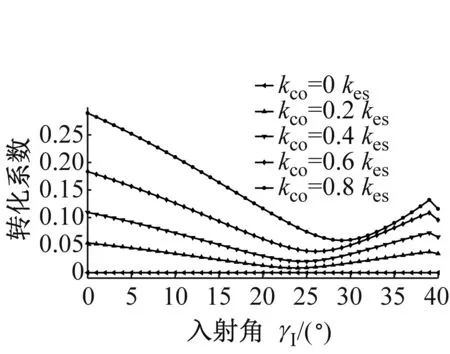
(f) TSH→SV
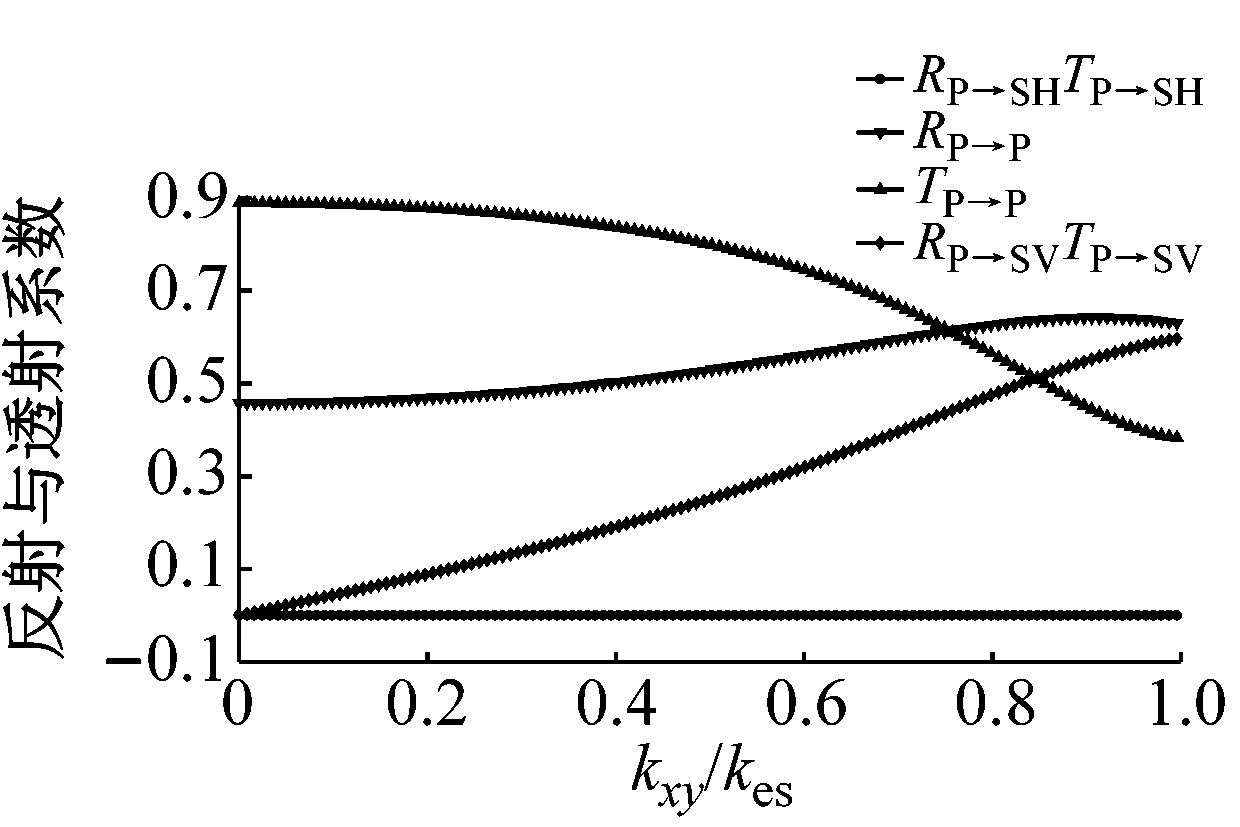
(a) 变量为kxy,且此时kzy=kzx=0
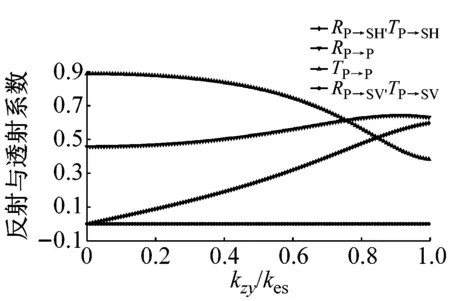
(b) 变量为kzy,且此时kxy=kzx=0
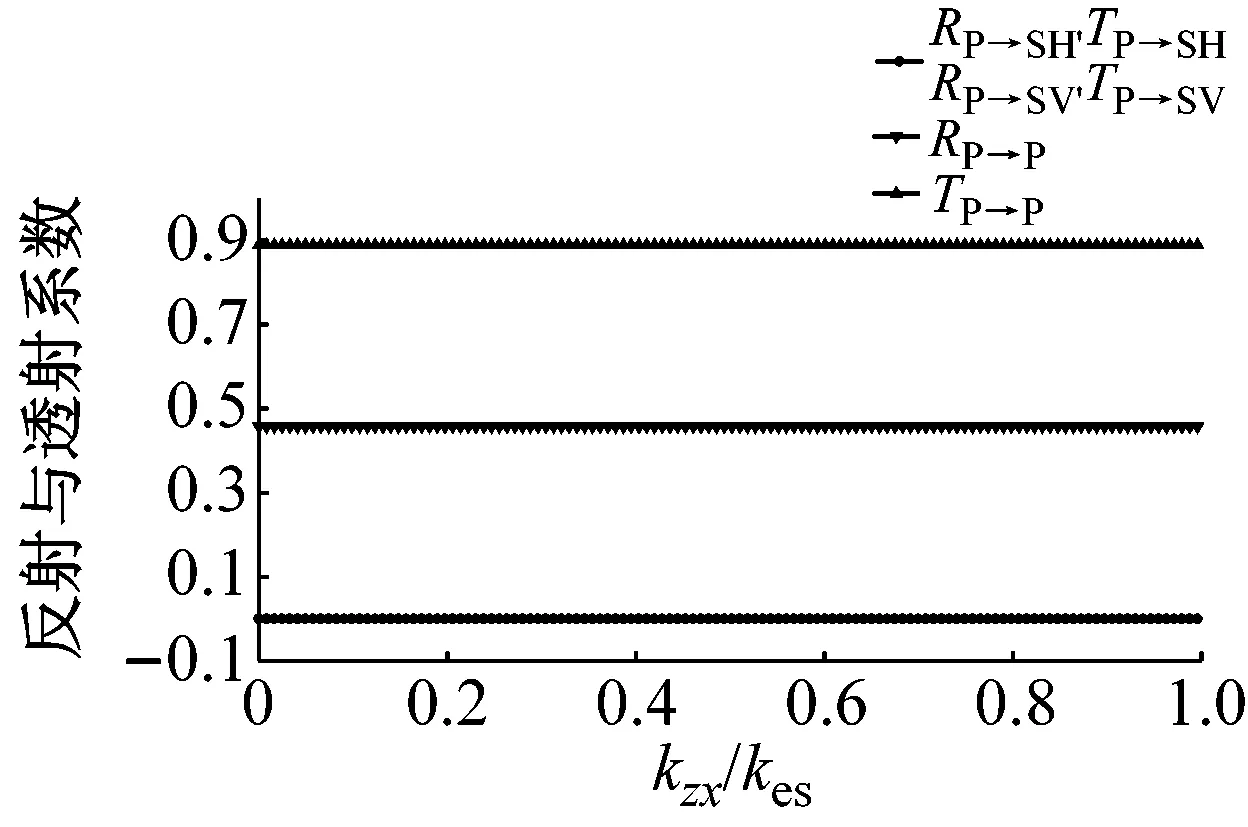
(c) 变量为kzx,且此时kzy=kxy=0

(a) 变量为kxy,且此时kzy=kzx=0
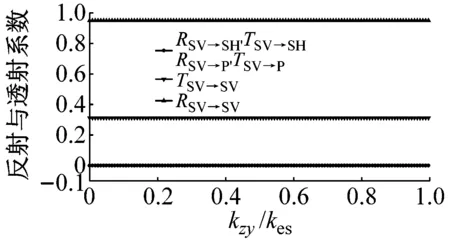
(b) 变量为kzy,且此时kxy=kzx=0
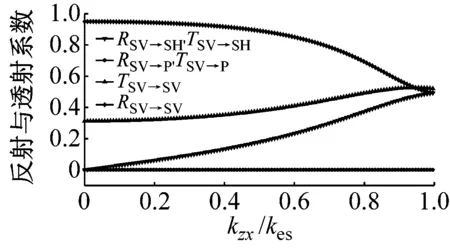
(c) 变量为kzx,且此时kzy=kxy=0

(a) 变量为kxy,且此时kzy=kzx=0
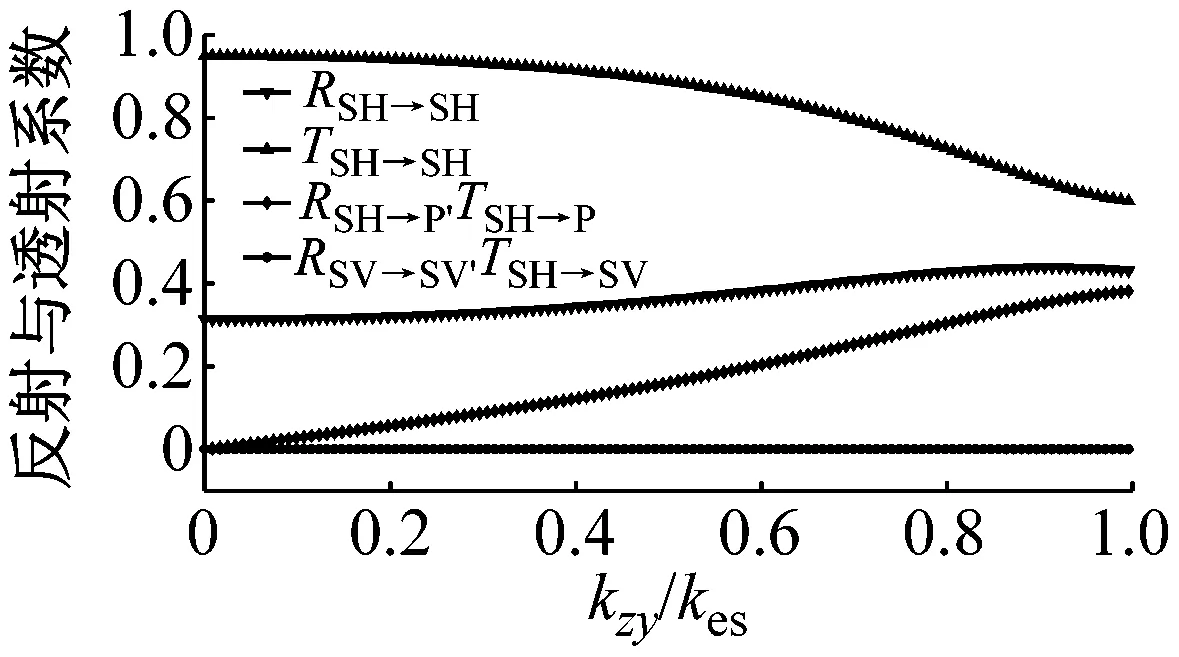
(b) 变量为kzy,且此时kxy=kzx=0
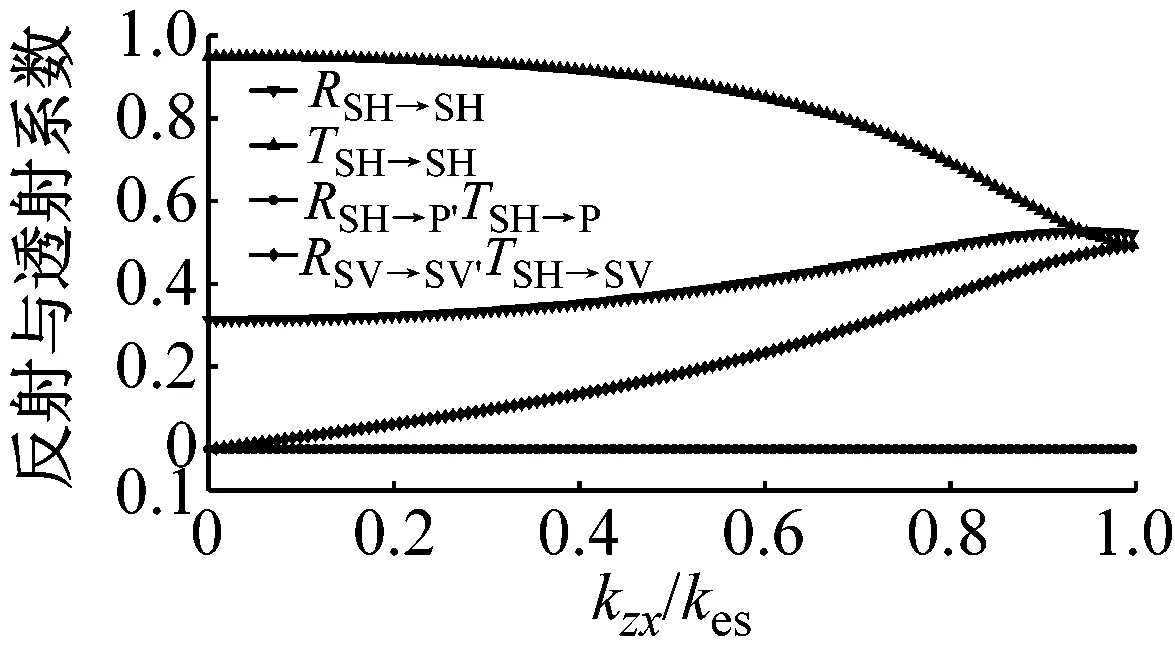
(c) 变量为kzx,且此时kzy=kxy=0
(3) 相对于以往采用仅存在主刚度系数节理描述应力波折反射规律的研究,节理中交叉耦合刚度系数的存在相当于是对原模型的扩展,交叉耦合刚度系数控制了应力波能量流向。
本文对三维岩石节理应力波传播规律初步探讨和分析,通过变形刚度系数考虑了由于复杂节理表面形态对应力波折反射规律的影响。本研究有利于加深对岩体动力学的理解,对于岩土地震工程和工程物探具有一定的积极意义。然而本文由于采用线刚度模型描述低幅值应力波入射时的力-变形行为,忽略由于较大变形节理面嵌合度变化等现象带来的非线性力学变化规律,因此不适用于高幅值应力波入射的情形。因此下一步工作应该结合数值计算与实验工作对高应力幅值应力波入射三维节理的传播行为进行研究。
