一维热传导过程的计算模拟
2018-08-27陈大伟斯小琴
陈大伟, 斯小琴
(安徽建筑大学城市建设学院 a. 教育处; b. 基础部, 安徽 合肥 238076)
如果物体内各点的温度不同,就有热量从温度较高地方流向温度较低的地方.在不少生产实际问题中,经常需要考察物体上各点的温度随时间分布状态,这就要求解各种定解条件下的热传导方程.一维热传导方程是热传导方程的最简单形式,但是求解和对结果的理解说明并不简单,这也使得此问题成为该领域的一个热点问题.当前有通过分离变量法与其他方法相结合获得解析解,该类方法避免不了繁琐的积分微分运算,并且对复杂的结果很难做易理解的说明[1-3];也有很多通过差分法和其他一些延伸方法可给出较高精度的数值解,但都涉及到高级计算机程序或较复杂的数学计算,这就使得在工程实际中直接运用比较困难,并且对所获得结果未能作出较全面和直观的解释[4-12].本文通过办公软件Microsoft Excel,可不用进行语言编程即可快速获得一维热传导方程高精度数值解,并通过OriginPro 8.0将巨大量的数值解数据模拟成温度的时空分布曲面图,方法简单实用,结果形象直观[13].
1 模型与方法
考察一个简单模型,如均匀细杆内热量传播过程.设细杆侧面绝热,热量只能沿轴向传导.又设细杆横截面面积为常数A且很小,以致在任何时刻,都可以把横截面上的温度视作相同,因此,是一个一维情形.图1是密度为ρ、比热为c、热传导系数为k的均匀细杆.

图1 传热细杆模型Fig.1 The model of heat transfer rod
取x轴与细杆重合,以u(x,t)表示x点t时刻温度,则有
ut=a2uxx+f(x,t).
(1)
现将温度u(x,t)在(x0,t0)点沿x向前、向后h展开为泰勒级数,有
由式(2)和式(3),可得
(4)
将温度u(x,t)在(x0,t0)点沿t向前τ展开为泰勒级数,有
将式(5)整理,得
(6)
联立式(1)、式(4)和式(6),有
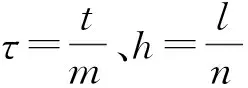
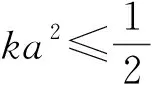
2 数值模拟结果及分析
考虑一实际问题,一根长为0.5 m的匀质传热枢轴,热扩散系数a2=4.5×10-5,它的初温为常数100 ℃,其两端的温度保持为0 ℃,考察该枢轴上温度的分布情况.
首先,该问题为一混合问题,即为:
(9)
取τ=1 s、h=0.01 m,其热传导方程的差分方程为
0.5 m的空间长度和3 000 s的时间长度组成的时空平面被分割成15 000个时空节点.在Excel中编写计算公式,并利用其下拉迭代计算功能迅速得到各节点的温度值.从细杆端点0 m处开始每隔0.1 m取一个特征位置点,一直取到终点,共取6个特征位置点.将所有特征位置点各时刻的温度值通过OriginPro 8.0模拟成温度-时间曲线(如图2所示);从0 s开始每隔100 s取一个特征时间点,一直取到400 s,共取5个特征时间点.将各特征时间点各位置点的温度值通过OriginPro 8.0模拟成温度-位置曲线(如图3所示).

图2 各特征位置对应的温度-时间曲线
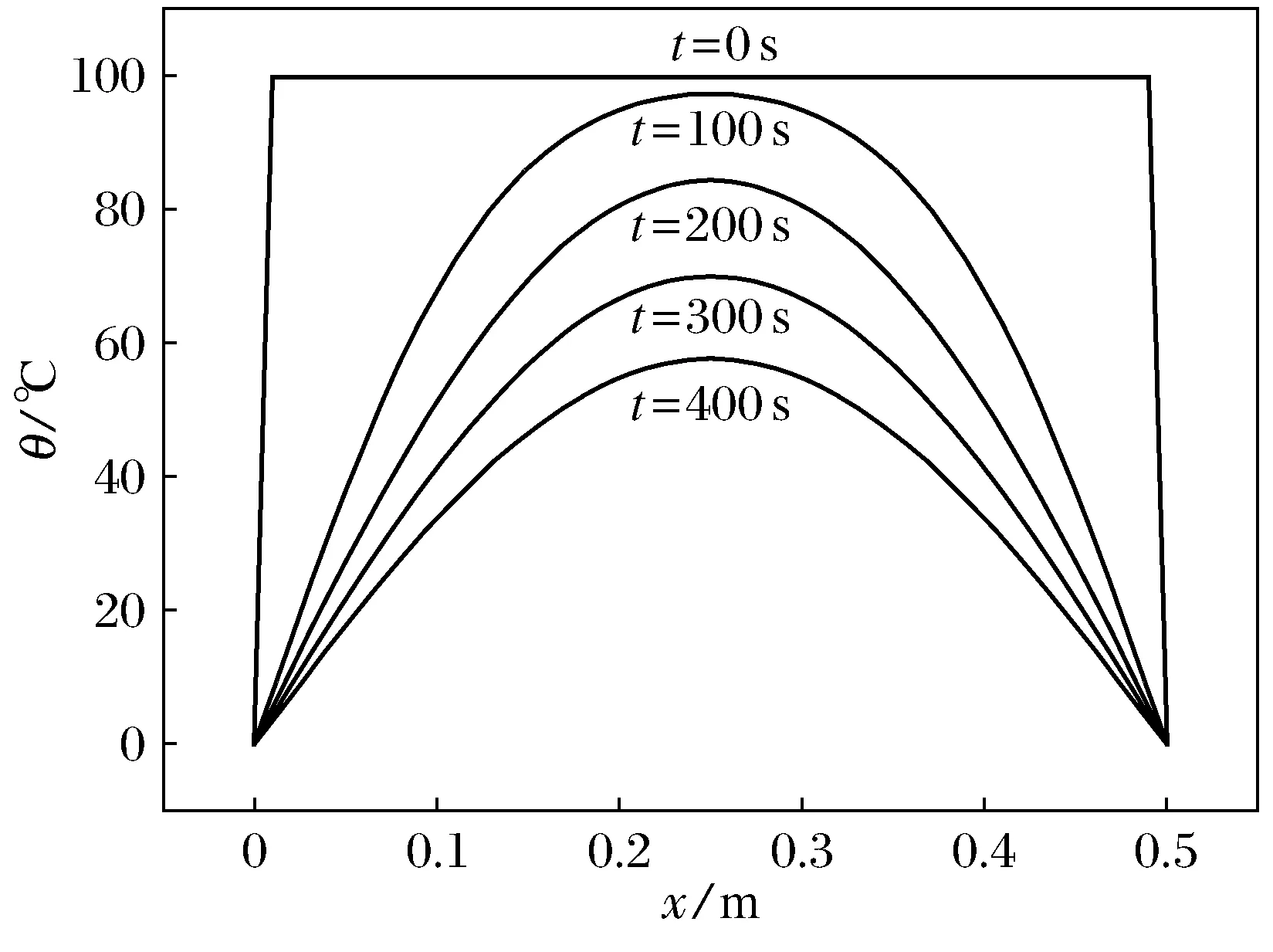
图3 各特征时间对应的温度-位置曲线
图2中0 m和0.5 m分别为端点位置.从图中可以明显看出,除两个端点位置温度恒定外,其他各考察点的温度都随着时间推移而降低,靠近端点处温度降低更快,而从时间角度考察,起初一段较短时间温度下降较“剧烈”,后期逐渐平缓;另外0和0.5、0.1和0.4、0.3和0.2 m位置处的时间-温度曲线重合,反映出两端点边界条件相同、传热枢轴匀质,各点温度变化也对称的性质.而从图3中可以发现,0 s之后各时刻传热枢轴温度呈现出两端低中间高,而且随着时间推移,各点(两端点除外)温度都在越来越“平缓”的降低;另外,各特征时刻位置-温度曲线左右对称形状与图2两条对应曲线重合相互验证.
图2、图3所反映出的传热枢轴各点温度随时间推移而降低且左右对称,与热量从高温的中部向低温的两端对称流失的实际完全相符.为将温度随时间、空间变化反映在一个图上,通过OriginPro 8.0将数据转化成矩阵,并通过该软件的Plot 3D Surface功能模拟三维图像.
由于温度在前期变化较快,为突出温度变化的影响因素,取前400 s所有数据绘制三维图像,如图4所示.为考察热传导后期特点每隔200 s取数据直至3 000 s,并将其模拟三维图像,如图5所示.

图4 前400 s温度时空分布曲面
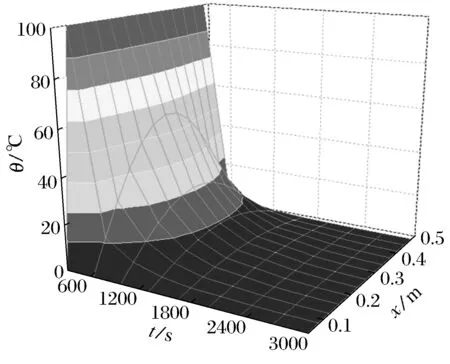
图5 前3 000 s温度时空分布曲面
在图4中,沿时间轴向前看,传热枢轴温度整体降低,且表现“前急后缓”的整体特征;沿位置轴向前看,传热枢轴温度两端低中间高,且表现“左右对称”的整体特征.这些特征与图2、图3所反映出的特征是一致的,但图4对特征信息的反映更整体、全面、集成,且通过不同灰度对比,更直观形象.
图5是图4在时间上的继续延伸,从图中可以发现温度“越来越平缓”地下降,以至于到1 800 s后整个枢轴上各点温度相差无几,各位置点温度随时间变化也几乎为零,温度的时空分布近似为平面,此时接近于“稳态”,这一特征与工程实际相吻合.
3 结 论
(1) 只要满足稳定条件,且时间、空间步距足够小,利用热传导方程的差分格式就可以获得一定精度要求的热传导方程数值解.
(2) 步距取值小,将时空平面分成的网格节点数量大,计算量就很大(本文计算15 000个时空节点).但是利用基本办公软件EXCEL的下拉迭代计算功能可以快速、简便地完成大量节点的温度计算.
(3) 利用Origin将产生的大量数据绘制成三维曲面图,能直观地得到热传导媒质上的温度时空分布,该方法所得到的结论与工程实际相符.
(4) 对于传热媒质中有热源即热传导方程中有非齐次项f(x,t)时,此方法同样适用.
(5) 本文利用最简单办公软件获得一维热传导数值解,并通过Origin将数值解数值模拟成相应 图像.该方法获得与其他方法同样的结果[15-16],但过程简单、快捷、方便,在解决此类工程实际问题中有一定的参考和使用价值.
