钢铁生产中具有不干涉约束的双吊机调度问题

谢 谢, 周 莉, 郑勇跃

(1. 沈阳大学 装备制造综合自动化重点实验室, 辽宁 沈阳 110044; 2. 中国标准化研究院, 北京 100191; 3. 辽宁省标准化研究院, 辽宁 沈阳 110004)

钢铁工业是世界经济中的核心工业,是工业化、现代化、经济发展的有力象征, 引领着建筑业、造船业、机器制造、家电和汽车业等其他工业的发展.钢铁生产是包括炼铁、炼钢、连铸、精炼等多阶段的生产模式,有关钢铁生产不同阶段的详细描述见文献[1],其中精炼阶段是生产中最基本的模式.在精炼阶段,钢包内融化的钢水首先由台车运输,再经由共享同一空中轨道的,平行的吊机将钢包装载到精炼炉上(见图1).这个过程对于吊机来说可以看做装载移动.装载移动结束后,吊机空载移动到台车上实施下一个装载移动.一旦钢包内钢水精炼结束,吊机将钢包从精炼炉卸载到台车上.

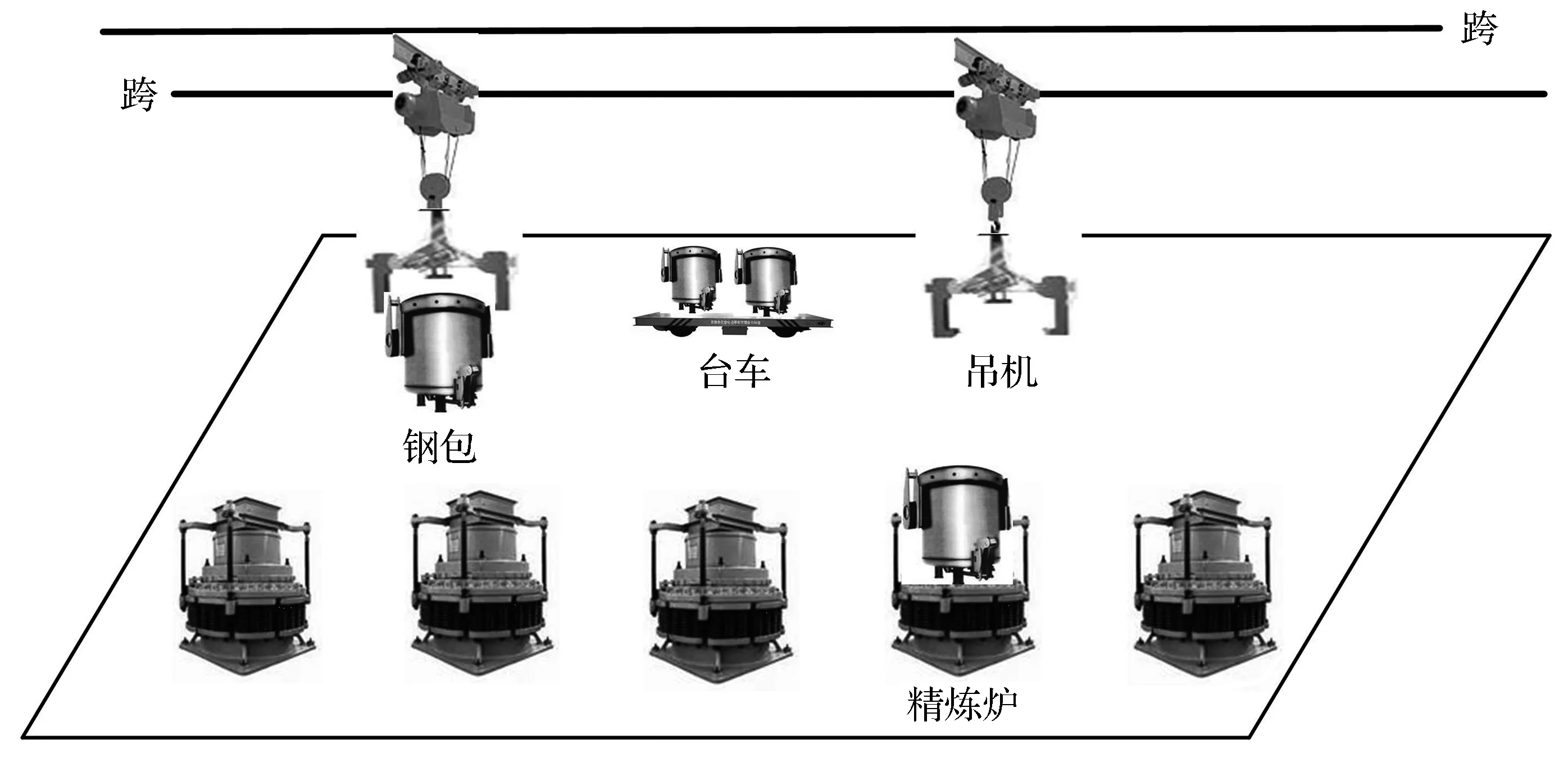
图1 精炼车间中两台吊机的布局示意图Fig.1 Layout with two cranes in a refining shop

吊机是钢铁企业实际生产中的稀缺资源,通常精炼区域上方有2台吊机共享同一跨.吊机移动时它的抓取设备(吊钩)不但沿跨方向移动,同时可以在跨间移动,这种方式可以使吊机移动到区域的各个位置.吊机间的工作是同步的,每次最多对1个钢包进行操作.精炼过程不允许任意两吊机的交叉或碰撞(吊机间的不干涉要求).图1以5台精炼炉为例,当1台吊机对1个精炼炉实施操作时,另1台吊机不能跨越当前的这台吊机,也就是吊机调度服从不干涉约束.2台吊机的调度影响着炼钢过程的完工时间.因此,该过程的主要目的就是确定吊机的装载移动顺序,以最小化需要精炼钢水的结束时间,也就是最小化最后1个钢包精炼结束的时间.

迄今为止,受到多数关注的吊机调度问题的文献主要集中在装箱港口码头终端的背景,该类问题首先由Daganzo[2]提出,即使是优化吊机调度以最小化1艘船只的最大完工时间,问题已经被Zhu等[3],Lim等[4],Lee等[5]证明为NP完备的.当考虑多吊机同时调度时,吊机在同一跨上彼此不能交叉的约束首先由Kim和Park[6]提出,对于跨上具有任意数目的吊机,Lee等[7],Lim等[8]提出并证明了一些最坏性能比为2的算法.Zhang等[9]改进了所提出算法的界,并证明了对于任意m个吊机,算法的最坏性能比为2-2/m+1<2.

不同于以上的吊机调度及经典的生产调度问题,本文考虑的吊机调度问题需要满足钢铁企业实际生产的具体要求,问题集中在钢铁企业的精炼环节,而精炼过程伴随着大量的物耗和能耗,尤其是吊机间为避免相互干涉或碰撞,或经常出现不必要的等待,或延长了等待时间,或额外增加了空载移动时间,一台吊机调度不好往往造成资源、能源的消耗和环境的污染.此外,大多数文献只是考虑了吊机的装载、卸载,忽略了吊机的移动时间.虽然谢谢等[10-11]考虑了吊机的移动时间,但与本文研究的问题不同,文献[10-11]只考虑了吊机作为生产过程的唯一运输工具,并没有考虑与台车等工具的协调.由于吊机是稀缺资源,一般精炼车间内通常有2～3台吊机,本文主要研究2台吊机的调度,考虑吊机间的干涉时没有忽略吊机移动时间.此外,从吊机运作角度考虑适合钢铁实际生产的简单易行的方法.

1 问题定义和描述

本文定义最大完工时间为需要精炼的钢水最大完工时间,为精炼结束后,最后1个钢包从精炼炉卸载到台车上的时间.本文考虑的问题是调度2台吊机,且避免交叉最小化需求精炼钢包的最大完工时间.

给定L个钢包在台车上等待精炼.为了方便表达,文中余下的部分定义台车的位置就是钢包的初始位置及最终位置.由于该位置固定,可以预先计算出吊机在任意两位置间的距离.

给定从左至右沿跨方向有F个精炼炉, 由于炉子和钢包的位置预先已知, 吊机在任意两点的距离和时间都是可以计算的.每个吊机每次只能吊起1个钢包, 每个炉子1次只能加工1个钢包.

由于所研究的问题是NP-难的,所以不可能在可以接受的时间内求得大规模问题的最优解.因此,提出求解问题的启发式算法,并对算法进行最坏性能分析.

2 启发式算法及最坏性能分析

算法首先从左至右将L钢包平均分成F个子集.计算每台吊机当前位置空载移动到台车提起钢包、装载移动到精炼炉后再放下的时间.

第1步 从左至右将F个子集形成列表,将该列表按照每台吊机的总操作时间平均分成2部分.

将具有相同钢包数的2部分共享处于列表中间位置的精炼炉,也就是一些共享精炼炉的钢包分配给1台吊机,剩下的钢包分配给另1台吊机.下文将这些共享的精炼炉称为交叉精炼炉.

第2步 对于可交叉部分的精炼炉,将钢包分配给最早可能空闲的吊机,一旦2台吊机可同时操作,则将精炼炉分配给另1台吊机.

第3步 分配每一个部分给对应的吊机.

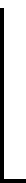
(1)

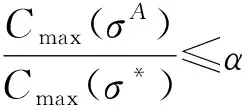
性质1 对于2台吊机的问题,启发式算法的最坏性能比为4/3.

证明 讨论以下2种情况.

情况1 交叉精炼炉属于第1部分.

根据算法第2步,则有

即

(2)

(3)

结合式(1)、式(2)得:

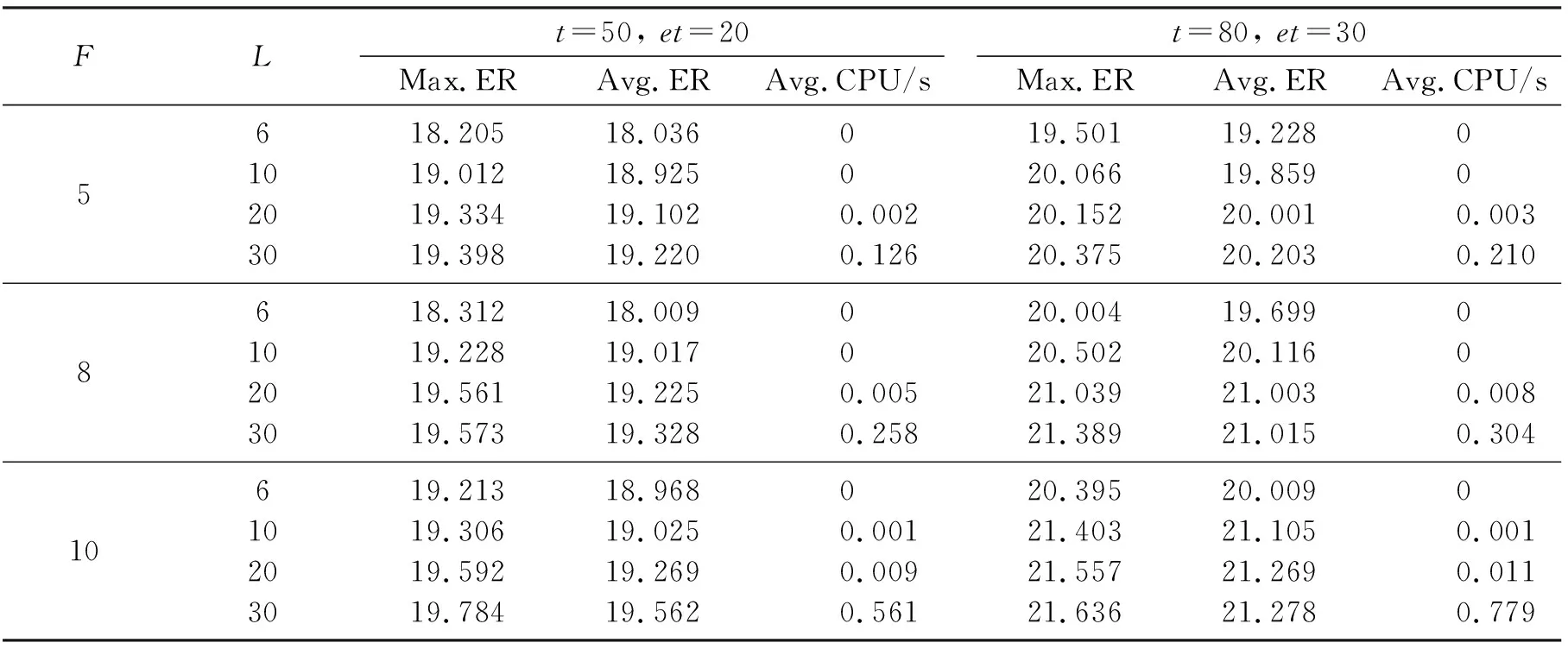
a

(4)

(5)

情况2 交叉精炼炉属于第2部分.

根据算法第2步,有:

因此有:

结合式(1)和式(6),得

a≥b.

(8)

在这种情况下,根据式(8)及不交叉约束,则有

(9)

结合式(1)和式(8),有

根据式(7)和式(9),

3 计算结果

利用数值计算实验验证算法的有效性,表1证明了对于小规模实例算法的最优间隙.算法采用C# 5.0语言编程,并且根据钢铁企业生产实际的数据求解了一系列问题的实例.此算法在内存为8 192 MB RAM和i7-3770 3.4 GHz的x64位计算机上用Visual C++语言编码进行了测试.每个实例考虑的参数如下:

(1) 装载移动时间t在[30, 100]之间离散平均分布随机生成;

(2) 空载移动时间et在[10, 50]之间离散平均分布随机生成;

(3) 钢包和精炼炉的数目分别在[6, 30]和[5, 10]之间离散平均分布随机生成.

算法的质量由跟下界LB的相对偏差(Cmax(σA)-LB)/LB*100%来度量,算法的平均误差比(Avg.ER)、最大误差比(Max.ER),以及算法的平均计算时间(Avg. CPU)用来度量测试实例的性能.由表1可以看出,随着问题规模、精炼炉、钢包数目的增加,所提出的启发式算法的质量平均偏差低于22%.对于一组最小规模的问题,相比加工时间,吊机的移动时间很短,可以忽略.因此,该算法可以产生最优解.当精炼炉的数目与钢包数目不接近时,解的质量保持稳定.对于小规模实例,算法可以迅速获得问题的解.对于较大规模问题,算法的计算时间也不超过1 s.

表1 启发式算法与下界比的平均最优间隙Table 1 Average optimality gaps of the lower bounds with respect to the heuristic algorithm

4 结 论

本文研究钢铁企业精炼车间的双吊机调度问题,考虑吊机间的不交叉约束,目标函数为最小化给定钢包的最大完工时间.探究了问题的最优性质,并提出1个启发式算法,进一步证明了该算法的最坏性能比为4/3.数值计算结果表明所提出的算法可以产生问题的近优解,最大偏差不超过22%,求解的时间不超过1s.未来的研究考虑扩展到更多吊机同时移动的问题.