基于短时滑移模糊熵和LPP的轴承故障诊断
2018-08-25童水光张依东从飞云
童水光, 张依东, 徐 剑, 从飞云
(浙江大学工学部 杭州,310027)
引 言
振动信号是旋转机械设备动力学特征的表现形式,具有非线性、非平稳的特性[1-2]。信号处理与分析是机械设备健康状态监测的重要依据。近年来,不同的特征提取及诊断方法不断涌现,短时傅里叶变换、小波分析及经验模态分解等时频分析方法被广泛应用于非线性、非平稳信号分析领域,并取得了一定成果。但这些方法存在一些不足,短时傅里叶变换由于选用固定的时间窗函数,无法分析时频分辨率有变化的非平稳信号。小波变换是一种采用有限长度小波基函数的分析方法,易产生能量泄露,从而影响时频能量分布的定量分析和结果精度。经验模态分解对多分量信号易产生模态混叠现象,从而导致错误的固有模态分量(intrinsic mode functions,简称IMF)分量,失去了具体的物理意义。
熵能实现对信息的量化度量,有效表征时间序列复杂性,被广泛应用在机械设备故障诊断领域。Pincus[3]首次提出近似熵的概念。Chen等[4-5]用模糊理论的汇总隶属度函数代替硬阈值判据,提出了模糊熵(fuzzy entropy, 简称FEn)并取得了较好的测试效果。但样本熵和模糊熵都只从单一尺度衡量时间序列的复杂性[6],文献[7]提出了多尺度模糊熵(multiscale fuzzy entropy,简称MFEn)方法,通过引入尺度因子实现从不同时间尺度上描述序列的无规则化程度[8]。对于冲击特征相近的不同故障信号,多尺度模糊熵无法取得较好的分辨效果[9]。
作为一种非线性降维方法,流形学习用于解决非高斯高维数据本质特征的提取问题,并使得利用非线性低维特征等价表示高维数据成为可能[10]。典型的流形学习算法有等距映射、局部线性嵌入(locally linear embedding,简称LLE)及LPP等。其中,LPP是一种考虑样本局部流形信息、无监督的特征提取算法。对于非线性流形结构,LPP通过保持数据的局部信息来有效逼近数据的真实分布,具有一般算法没有的非线性流形学习能力。文献[11-12]在特征映射(laplacian eigenmaps,简称LE)算法线性化处理的基础上,提出了LPP算法,并将其应用于人脸识别。李国芳[13]结合二维主成分分析(two-dimentional PCA,简称2DPCA)与LPP算法,增强对人脸图像特征的提取能力。张晓涛等[14]提出一种多尺度正交主成分分析(principal component analysis,简称PCA)和LPP相结合的方法,消除投影分量间的冗余信息,提高了故障的辨识率。丁晓喜等[15]结合小波包分解和LPP算法,实现挖掘故障信号潜在的特征信息,并对轴承故障及故障不同的损伤程度进行了诊断。王广斌等[16]提出多尺度子带样本熵方法,并与LPP相结合对轴承故障特征进行提取,能有效诊断轴承故障。
笔者提出一种基于短时滑移模糊熵和LPP的故障特征提取方法。该方法利用多尺度复合模糊熵对时间序列的表征能力,通过对滑移截断短时序列的架构分析[17],获得信号在不同复合尺度下的特征信息和故障潜在特征,再结合LPP学习非线性流形结构的能力。仿真信号和实验数据分析表明,该方法的滤波效果优于其他传统滤波方法。
1 基于多尺度复合模糊熵和LPP的特征提取方法
1.1 多尺度复合模糊熵
文献[7]利用粗粒化序列获得多尺度时间序列,提出了多尺度模糊熵方法,有效克服了模糊熵只能反映单尺度时间序列信息的不足,但是无法对冲击特征较为相近的不同故障信号取得较好的分辨效果[9]。多尺度复合模糊熵具体算法如下。
1) 设定模式维数m、相似容限r和尺度因子τ(1≤τ≤scale),对时间序列X={x1,x2,,xN}进行粗粒化,建立新的粗粒时间序列。根据间隔因子将粗粒时间序列不断向后滑移,构造滑移粗粒时间序列为
(1≤j≤(N-k)/τ;1≤k≤τ/p)
(1)
其中:p为滑移间隔因子。
当τ=1,p=0时,yk,j(1,0)即为原始时间序列。对于非零的τ和p,原始时间序列{Xi}构造成[τ/p]维的滑移粗粒时间矩阵。其中,第k行滑移粗粒时间序列被分割成(N-k)/τ段、长度为N/τ的粗粒时间序列{yk,j(τ,p)}。

(2)
对于[τ/p]维的滑移粗粒时间矩阵为
(3)
3) 对于维数m+1,重复步骤1~2,得到Bm+1(r)。
4) 对尺度因子为τ时的滑移粗粒时间矩阵计算模糊熵
FEn(τ,p)=lnBm(r)-lnBm+1(r)
(4)
5) 得到多尺度复合模糊熵的表达式为
(5)
其中:scale为尺度因子;p为滑移间隔因子;m为模式维数;r为相似容限;N为数据长度。
从以上步骤可以看出,尺度因子scale和滑移间隔因子p的选取对多尺度复合模糊熵的影响紧密。模式维数和相似容限的选取也非常重要,一般m=1或m=2,0.1std≤r≤0.25std(std为标准差)。
1.2 LPP流形学习
局部保留投影是一种经典的线性技术,可以沿着最大方差的方向投影数据。当高维数据位于嵌入在外围空间的低维流形时,通过找到拉普劳斯算子在流形上本征函数的最优线性近似获得局部保留投影。因此,局部保留投影具有如拉普拉斯特征映射和局部线性嵌入等优点。
n个高维样本X={x1,x2,,xn}通过非线性变换矩阵W投影降维得到一组向量矩阵Y={y1,y2,,yn}(WTX=Y)。
其目标函数为
(6)
其中:Sij为权值矩阵。
Sij采用k近邻法定义为
(7)
其中:xj为xi的第j个临近点;λ为大于0的常量。
k值取决于分析数据,常用方法是利用交叉验证法选择最优值。在实际应用中,k值一般取较小值[18]。
给定约束函数YTDY=1即WTXDXTW=1,对式(7)代数变换,得到最后优化条件
(8)
求解式(8)最小值
(9)
则
WTXLXTW=λWTXDXTW=λ
(10)
1.3 基于滑移截断短时序列的多尺度复合模糊熵特征提取技术
离散时间序列X(k),k=1,2,,N,其中,N为时间序列长度。截断时间矩形窗函数为
(11)
通过窗函数短时截断时间序列,获得新时间序列
yi(k)=x(k)w(k-(i-1)s)
(12)
其中:yi为第i次截取后获得的短时序列;s为滑移参数。
分析长度Nw为短时序列yi的长度,选取Nw将离散时间序列分别滑移式截断成多个短时序列,提升为多维短时序列矩阵形式。其中,第i个短时序列为
Yi=[yi((i-1)sp+1),
yi((i-1)sp+2,,yi((i-1)s+Nw]
(13)
多维短时序列矩阵Y为
(14)
其中:m为截取短时序列的个数;Nw为分析长度。
定义滑移参数s的限定范围为
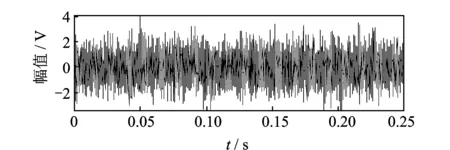
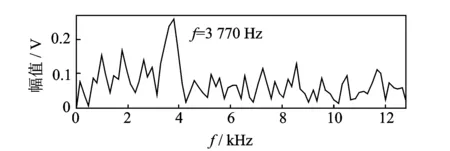
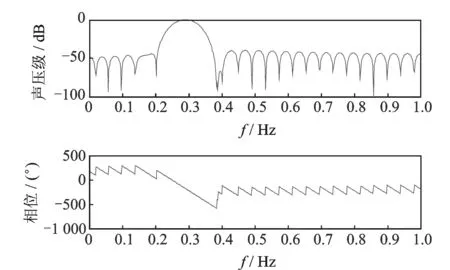
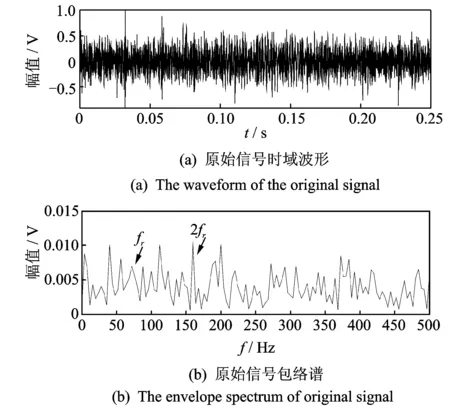
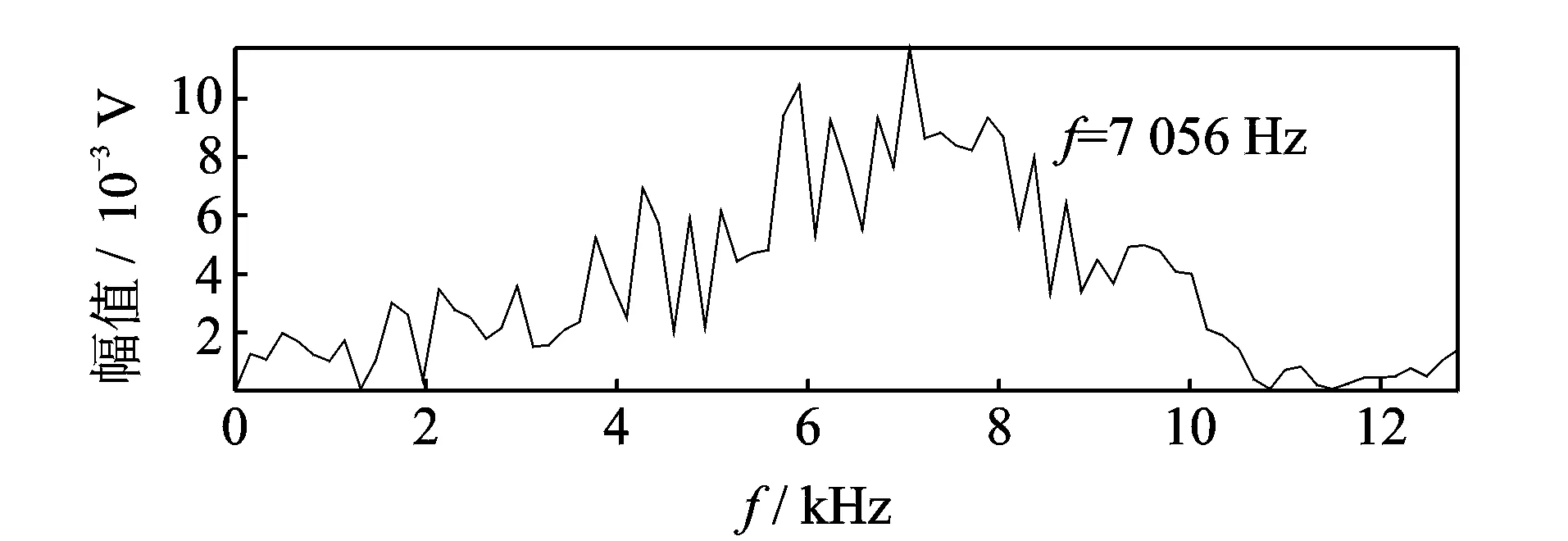
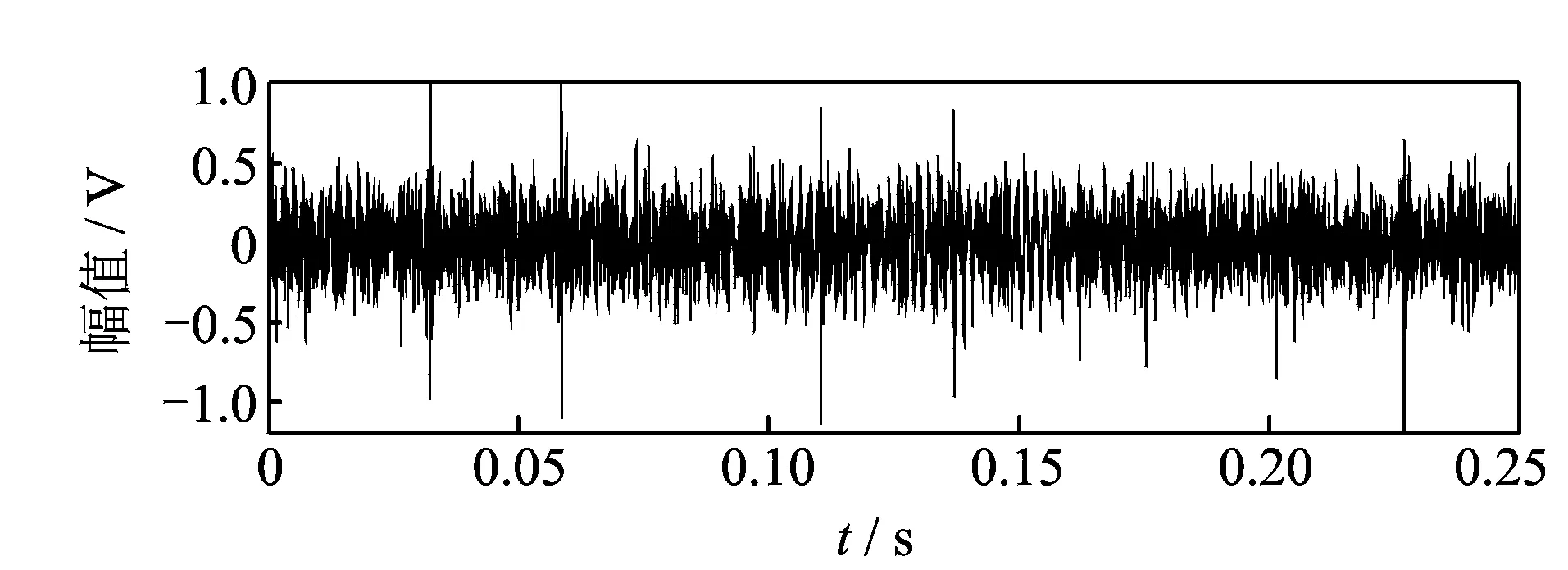
1 (15) 基于多尺度复合模糊熵和LPP的特征提取方法流程如图1所示。分别将多尺度复合模糊熵和LPP流行学习融入到多维短时序列矩阵Y,其中,第i个短时序列的多尺度复合模糊熵表达式为 RCMFEn(Yi)=FEni(1,2,,scale) (16) 利用LPP算法将多维短时序列的模糊熵矩阵降维压缩为一维向量,得到基于滑移截断序列的模糊熵特征向量En,其表达式为 En={RF1,RF2,,RFm} (17) 其中:RFi为第个短时序列的降维压缩多尺度复合模糊熵。 图1 基于多尺度复合模糊熵和LPP的特征提取方法流程Fig.1 The diagram of feature extraction based on refined composite multiscale fuzzy entropy and LPP En代表了对应短时序列时域信号段内的信息复杂度和模糊程度,用来描述信息的不确定性,获取最小模糊熵为 Y(z)=min|RF(i)| (i=1,2,,m) (18) 其中:z为最小模糊熵对应所在序列的编号。 根据轴承故障振动信号的冲击特性并结合短时序列滑移截断的架构思想,可知包含有丰富故障信息的短时序列的模糊性程度较低,对应着较小的模糊熵。因此,对包含有强故障冲击成分的短时序列进行重构 (19) 特征提取得到的包含最小模糊熵的短时时间序列,其衰减震荡是以其共振频率为主要周期的波形信号。根据冲击振动的产生机理,认为短时序列对应频域响应图中的主频带成分为原始时间序列的共振频带。 根据冲击震荡衰减模型原理,当滚动轴承发生故障,故障冲击信号为周期震荡衰减过程,其共振主频率包含有强故障冲击成分。结合滑移截断短时序列的特性和信息参数,设计出合理的最优带通滤波器来提取信号在共振频率处的信息,实现新的故障诊断识别技术。 最优滤波器的设计首先获得短时重构序列的频域响应图,其计算公式为 (20) 其中:y(n)为短时重构序列;Nw为短时序列的分析长度;Y(z)为短时序列对应的频域序列。 引入有限冲激响应(finite impulse response,简称FIR)数字滤波器,通过找到匹配的(fc,Δf)系数和滤波阶数来设计FIR滤波器G(f)。其中:fc为中心通过频率;Δf为G(f)的滤波带宽。FIR滤波器是通过对已知脉冲形状进行采样并用这些样本以相反的阶数作为滤波器系数,来设计匹配滤波器的脉冲响应。设计参数公式为 (21) 其中:fs为采样频率。 根据滚动轴承故障模型对滚动轴承外圈故障进行模拟,其表达式为 (22) 其中:τi为第i次冲击相对于平均轴T的微小波动。 图2 外圈故障仿真信号时域响应Fig.2 Time domain simulated fault siganl with outer race 设置对应采样频率fs=25 600 Hz,转频fr=12 Hz,外圈通过频率为fo=40 Hz,系统固有频率为fn=3 700 Hz。其中,信号包含信噪比为-12 dB的高斯白噪声。图 2为外圈故障仿真信号的时域响应,噪声几乎将故障特征淹没。 针对图 2所示的外圈故障仿真信号,利用笔者提出的方法进行故障信息的特征提取和诊断识别,设置滑移参数sp=6,分析长度Nw=156。图 3为短时重构序列的频域响应。得到系统共振频率fc=3 800 Hz,并设计最优带通滤波器,如图 4所示。滤波器滤波后的系统时域信号如图 5所示。可见,笔者提出的基于滑移截断短时序列的多尺度复合模糊熵方法,在滚动轴承的故障冲击特征识别方面具有很好的表现,能够在强噪声弱故障背景下有效提取故障的冲击成分,准确诊断出对应故障类型。 图3 仿真短时重构序列频域响应Fig.3 Frequency response of short-time reconstruction ser 图4 FIR滤波器幅值和相位频率响应Fig.4 Amplitude and phase response spectrum of FIR filter 图5 最优滤波器滤波后的时域信号Fig.5 The time series filtered by optimal filter 为验证基于短时滑移模糊熵和LPP的故障诊断方法的有效性,建立人工故障滚动轴承实验台并应用该诊断识别技术。实验台装置如图 6所示。该实验台主要由一级齿轮箱、伺服电机和磁粉制动器组成。该实验研究对象为30304和32207型的圆锥滚子轴承,通过电火花加工、人为制造不同尺度和类型的滚动轴承微小故障,如图 7所示,并在电机不同负载下模拟真实故障进行实验。实验选用NI9234数据采集卡,通过加速度传感器采集振动信号,设定采样频率为25.6 kHz,数据采样长度为6 400个数据点。 图8为采集的30304型轴承的振动信号和包络 图6 实验装置示意图Fig.6 The schematic diagram of experimental set 图7 轴承故障形式Fig.7 The fault types of rolling bearing 图8 30304型轴承信号及其包络谱Fig.8 The bearing signal of 30304 and its envelop spectrum 谱。该轴承故障类型是外圈宽为1 mm的横槽,输入转速为900 r/min,对应转频为15 Hz,根据理论公式计算外圈故障特征频率约为75.8 Hz。由于较强的背景噪声,无法从时域波形中观察出轴承故障周期性冲击特征,而包络谱由于受其他噪声频率干扰,无法辨识出外圈故障频率76 Hz。针对图 8的振动信号,利用本研究方法进行故障信息的特征提取和挖掘。参数设置如表 1所示,根据滚动轴承特性和比较分析,笔者选取截断分析长度为156,滑移参数为16。图 9为短时重构序列的频域响应,得出系统共振频率fc=7 056 Hz,并设计最优带通滤波器,得到滤波后时域波形及包络谱。 表1 参数设置 图9 短时重构序列频域波形Fig.9 Frequency response of short-time reconstruction series 图10 滤波信号的时域波形及其包络谱Fig.10 The waveform and envelope spectrum of the filtered singal 由图10所示,笔者提出的故障特征提取方法适用于滚动轴承冲击故障识别。从时域波形看,滤波后的时域响应具有明显的周期性冲击特性,整体背景噪声得到抑制。从包络谱看,故障特征频率76 Hz及其多倍频峰值非常清晰,可以诊断出轴承发生外圈故障。对振动信号进行自回归滤波器滤波处理与分析,并与图 10对比,图 11为经过自回归滤波器滤波后的时域波形。其故障冲击特征表现微弱,不能准确地观察出周期性的冲击故障特征,无法有效抑制背景噪声。 图11 自回归滤波器滤波后的时域波形Fig.11 The time series filtered by autoregressive filter prediction filter 通过分析结果可知,基于短时滑移模糊熵和LPP的故障诊断方法能够有效地从强背景噪声中提取出周期性调制信号,准确识别出故障冲击特征频率,从而验证了该方法对滚动轴承的故障特征提取和降噪抑制具有良好的效果。 提出一种基于短时滑移模糊熵和LPP的故障特征提取方法。通过滑移截断轴承振动信号,获得基于短时序列的多尺度复合模糊熵,并结合LPP流形学习,能够有效描述振动信号的复杂度和不确定性,实现对滚动轴承微弱故障的诊断。仿真信号分析和实验结果表明,该方法对滚动轴承具有良好的故障冲击特征提取和识别作用。与其他传统滤波方法相比,该方法能够有效抑制噪声,明显增强故障谱线,在微弱故障特征识别方面效果更好。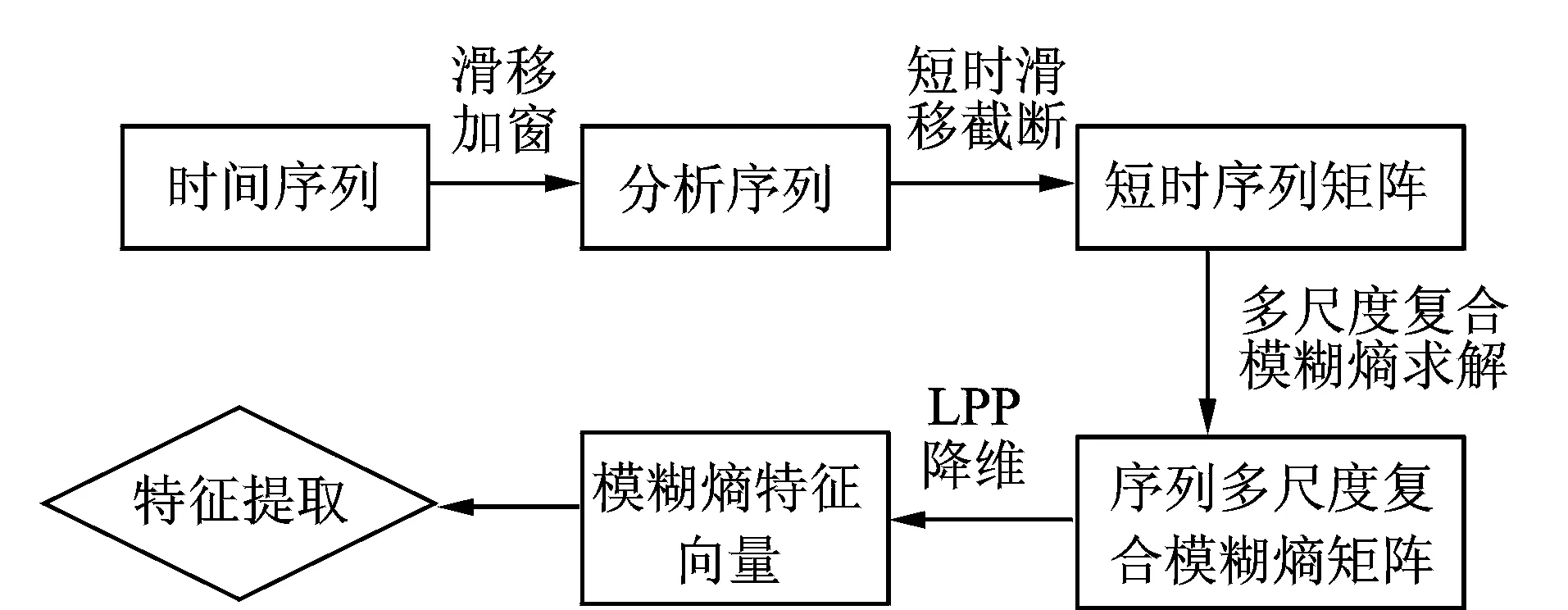
1.4 故障诊断识别技术
2 仿真与实验验证分析
2.1 仿真分析

2.2 实例分析




3 结束语
