温度载荷环境下LTCC基板的多目标结构优化
2018-08-24田文科王天石刘洋志仇原鹰
邓 超,田文科,王天石,刘洋志,仇原鹰
(1.中国电子科技集团公司 第二十九研究所,四川 成都,610036;2.西安电子科技大学 机电工程学院,陕西 西安,701071)
近年来,信息技术的发展要求高速数据和高电流密度传输,电子线路日益向微型化、集成化和高频化的方向发展。这就对电子元件提出了尺寸小、高频、高可靠性、价格低廉和高集成度的要求。LTCC(Low Temperature Co-fired Ceramic)是1982年诞生的新型材料技术,多层LTCC基板技术[1]能将部分无源元件集成到基板中,使得其具有高速、高频、高密度和高可靠性等优点,有利于系统的小型化,提高电路的组装密度,且有利于提高系统的可靠性[2-3]。该技术首先是将低温烧结陶瓷粉制成厚度精确而且致密的生瓷带,然后以生瓷带作为电路基板材料,在基板上利用激光打孔、微孔注浆、精密导体浆料印刷等工艺制出所需要的电路图形,并将多个无源元件 (如电容、电阻、滤波器、阻抗转换器、耦合器等)埋入其中,最后叠压在一起,在900℃烧结,制成三维电路网络的无源集成组件[4]。
LTCC基板 (以下简称基板)在使用中,由于温度场和结构场的共同作用,可能导致基板的某些部位因热应力过大而产生裂纹,进而导致基板上的电路发生断路失效。
针对因基板热应力过大产生裂纹而导致电路失效的情况,目前的分析方法有枚举法[5]、对比分析法[6]等。枚举法是通过给圆角附一个初始值R0,以ΔR为增量,逐一地增大圆角半径并计算各半径下基板的应力分布,最后选出合适的圆角半径R;对比分析法是通过改变热应力较大位置处的特征形状、结构尺寸等,并对不同的修改方案分别进行仿真计算,然后对仿真结果进行对比分析,最后根据变化趋势选取比较合理的结构形状和特征尺寸。但是对于特征较多的基板模型,其对应的设计变量也较多,采用上述方法比较复杂且工作量大、设计效率低,难以得到考虑全局应力降低的最优解。因此本文采用响应面分析法和多目标遗传算法,结合有限元分析软件,对基板进行多应力目标的优化问题研究。
1 基板的热应力仿真
1.1 基板的实体三维模型
使用三维建模软件Pro/E建立基板的三维实体模型。基板的实体模型由七层LTCC单板组成,层与层之间通过浆料叠压在一起,在900℃烧结成型。基板总体尺寸为61.40 mm×30.75 mm,总厚度为1.692 mm,如图1所示。
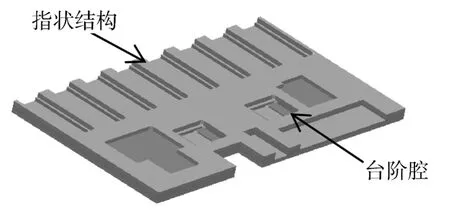
图1 基板模型图Fig.1 Model of the LTCC substrate
1.2 基板的有限元模型及边界条件
基板的弹性模量为82 GPa,泊松比为0.26,密度为2.45 g/cm3,热膨胀系数在25~300℃为7.0×10-6/℃。基板网格尺寸取为1 mm,在厚度方向采取扫掠划分,每层基板都划分3层网格,划分结果如图 2所示,其中节点数:170572,单元数:30525。
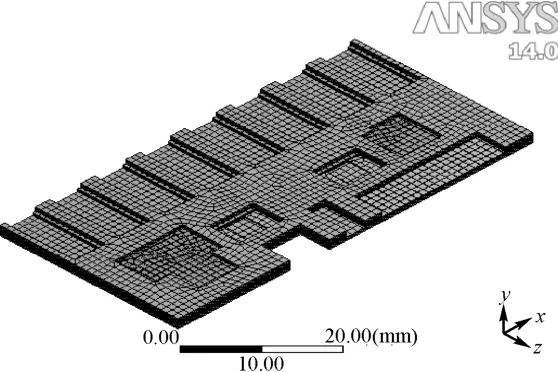
图2 基板的网格模型Fig.2 LTCC substrate grid model
基板底面通过焊料焊接在盒体上,因此将基板整体模型的底面设置为固定约束。同时对基板模型整体施加最高试验温度,即产生最大应力的125℃温度载荷。
1.3 应力分析结果
由有限元软件分析结果可得,应力较大的地方主要发生在指状结构倒圆角处和台阶腔体倒圆角处,如图3所示,应力单位为MPa。 (图中的目标1,2,3分别代表箭头所指处的圆角应力最大值,将其作为后续优化设计中的目标函数)。
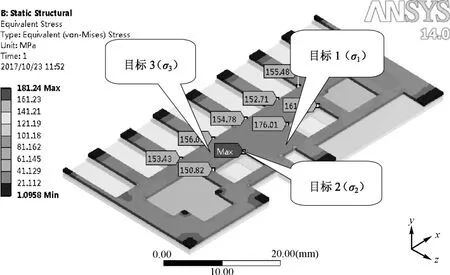
图3 基板应力云图Fig.3 Stress nephogram of the LTCC substrate
2 多目标优化设计
2.1 优化数学模型
影响基板结构应力的指状结构特征主要包括指状结构的宽度H和倒角R,如图4(a)所示;影响基板结构应力的台阶腔结构特征主要包括台阶腔边距L和V、倒角R,如图4(b)所示。
将影响基板应力的上述4个尺寸特征设置为设计变量,见表1;选取基板应力较大的3个部位的应力作为目标函数 (参见图3)。采用遗传算法进行多目标优化,对基板结构进行尺寸优化设计。
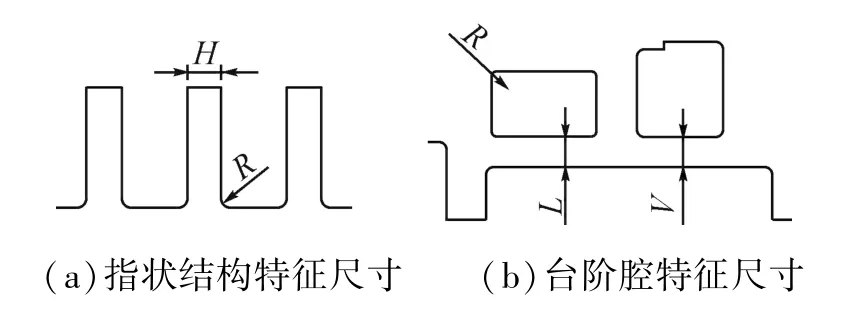
图4 影响基板应力的特征尺寸图Fig.4 Feature size graphs of affecting the stress of the LTCC substrate
(1)设计变量:
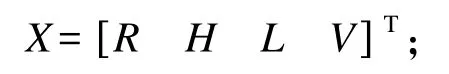
(2)约束条件:
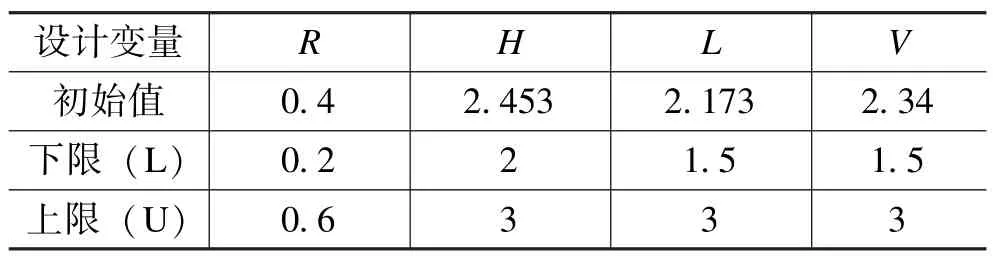
表1 设计变量的取值范围Tab.1 Range of the design variables mm
(3)目标函数:
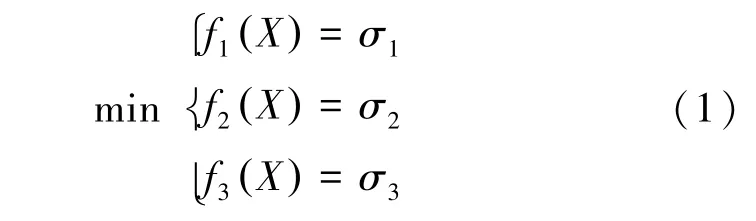
2.2 优化方法
(1)Pareto最优解
在多目标优化问题中,一个目标的改变往往会造成其他目标的变化,只有各分目标相互协调,才能求得比较接近的最优化方案。
多目标优化的求解过程中往往出现一些不能单纯地互相比较的解,即称为Pareto最优解或非支配解,它们的集合称作Pareto最优解集。
(2)多目标遗传算法
多目标遗传算法基于多目标优化设计,根据不同的权重分配条件,获得优化问题的全体最优解集。多目标遗传算法的基础特征是利用各代间包含潜在解的种群,进行多向性和全局性的搜索,因此是求解Pareto最优解集的一种有效手段[7]。
多目标遗传算法的基本流程是借助于适应值分配机制。本文采用的适应值分配机制方法为权重和方法,权重和方法是首先把权重分配给各个目标函数,之后通过加权求和把各个目标函数组合成为单一目标函数。优化过程结束后,需要进行归一化处理加权目标函数,从而完成对整体最优解的选取。单一目标函数表示如下:
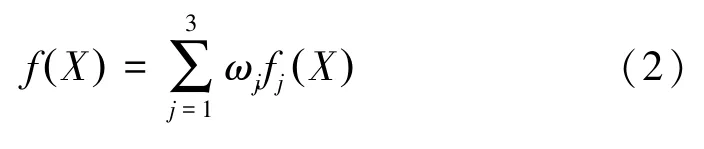
式中:f(X)是总目标函数;fj(X)表示第j个目标函数;ωj就是第j个目标函数在总目标函数中的权值,权值求和应满足公式:
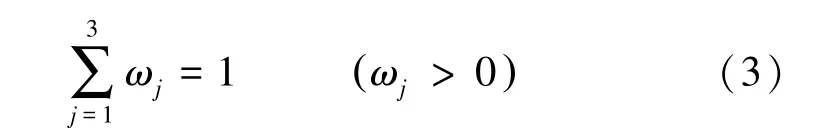
本文选取的3个目标函数 (基板3个倒角处的最大应力)在基板使用中的重要性是一致的,因此在权重分配上也是一致的,则各个目标函数的权值为:
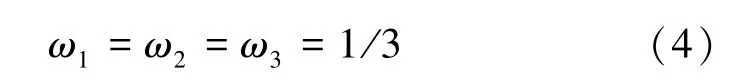
本文总目标的初始值为:
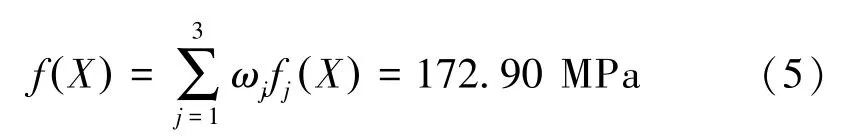
2.3 灵敏度分析
局部灵敏度图表能够观察输入参数对输出参数的影响程度。其中不同的颜色条表示相对应的输入参数。在结构优化中,当设计变量个数大于目标函数个数时,通过灵敏度分析可得到为实际应用各种迭代法实现最优化而需要的设计变量。基板优化结果的局部灵敏度如图5所示。
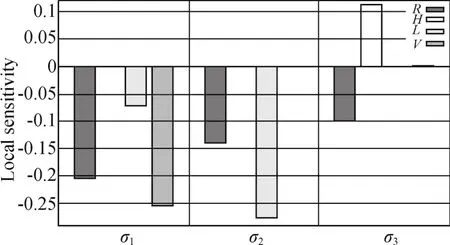
图5 基板优化结果的局部灵敏度示意图Fig.5 Local sensitivities graph of the optimization results of the LTCC substrate
由图5可得特征尺寸R、L和V对σ1的影响较大且均是递减关系,而特征尺寸H对σ1影响十分微弱;特征尺寸R和L对σ2的影响较大且均是递减关系,而特征尺寸H和V对σ2的影响十分微弱;特征尺寸R和H对σ3的影响较大,其中R对σ3为递减关系,H对σ3为递增关系,特征尺寸L和V对σ3的影响十分微弱。灵敏度示意图也完全符合腔体结构应力 (σ1,σ2)与结构特征尺寸 (R、L、V)、指状结构应力(σ3)与结构特征尺寸 (R、H)对应的关系。
2.4 尺寸优化分析
分别研究灵敏度大的单个设计变量与单个目标函数之间的关系,可以表示为图6所示的响应关系曲线。
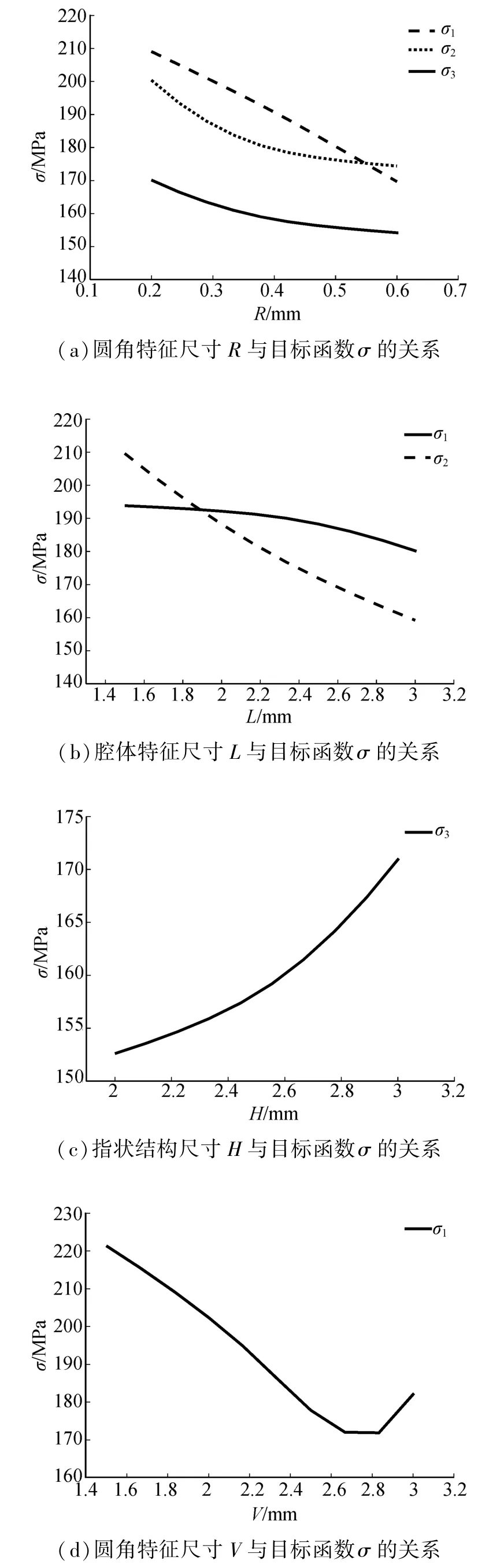
图6 单个设计变量与目标函数之间的影响曲线图Fig.6 Influence plats of a single design variable to the target function
从图6(a)可以看出,圆角特征尺寸R与σ1、σ2、σ3的关系均为单调递减,即随着圆角半径的增大,应力集中现象逐渐消失,应力逐渐减小;从图6(b)可以看出腔体特征尺寸L与σ1、σ2的关系均为单调递减,即随着L的增大,左腔体位置整体向基板中心偏移,应力逐渐减小;从图6(c)可以看出,指状特征尺寸H与σ3的关系为单调递增,即随着指状宽度的增加,导致两个指状之间的距离减小,指状间圆角的应力逐渐增大。从图6(c)可以看出腔体特征尺寸V与σ1为二次函数关系,且在 (2.7,2.8)之间存在一个V使得σ1最小,右腔体在向中心偏移,由于腔体比左腔体尺寸稍大,可能靠近上边界,因此存在一个转折点。
此外,设计变量的组合对目标函数的3D响应面[8]图也可以表示出来,图7(a)为结构特征尺寸R、V组合与σ1的3D响应曲面图,从图中可以看出,两个设计变量共同作用时σ1的最佳点;图7(b)为结构特征尺寸R和L与σ2的3D响应曲面图及最佳点;图7(c)为结构特征尺寸R和H与σ3的3D响应曲面图及最佳点。此外,其他设计变量的组合对目标函数的3D响应面云图也均可表示出来,本文在此不作列举。
2.5 结果与分析
综合灵敏度分析和尺寸优化分析,得到Pareto最优解。优化前后结构尺寸参数如表2所示,目标函数结果见表3所示。
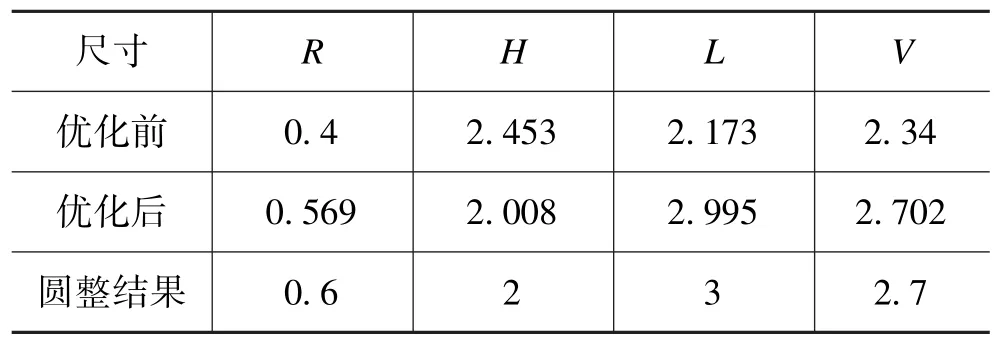
表2 优化前后结构尺寸参数Tab.2 Structure size parameters before and after optimization mm
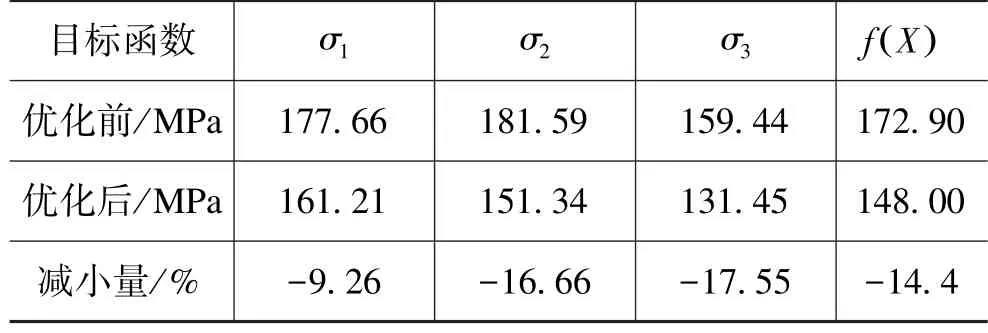
表3 优化前后目标函数结果对比Tab.3 Result contrasts of the target functions before and after optimization
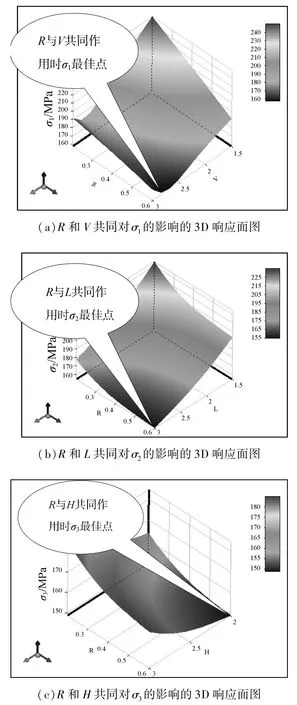
图7 设计变量与目标函数的3D响应曲面图Fig.7 3D response surfaces graphs of the design variables and the target function
从表3可以看出,总目标f X()减小了14.4%,其中σ1减小程度为9.26%,σ2减小程度为16.66%,σ3减小程度为17.55%。结果表明腔体处倒角和指状结构处的倒角应力都有比较明显的减小,使基板的电路质量有了显著的提高,有效降低了基板发生裂纹的可能性。
3 结论
本文通过应用有限元分析软件对基板模型进行热应力分析,可以获得基板的应力分布情况;然后综合采用响应面分析法和多目标遗传算法,通过灵敏度分析和尺寸优化设计,得到多应力目标函数的Pareto最优解。基板结构应力普遍减小,改善了基板的可靠性。同时对此类基板提供一种低应力的结构优化方法。
