基于ABAQUS-MATLAB联合仿真反演优化确定金属粉末成形本构模型参数

李璐璐，周 蕊，张建国，谢 东，吴孟丽



基于ABAQUS-MATLAB联合仿真反演优化确定金属粉末成形本构模型参数

李璐璐1，周 蕊2，张建国1，谢 东1，吴孟丽2

(1. 天津科技大学 机械工程学院，天津 300222；2. 中国民航大学 航空工程学院，天津 300300)

本构模型参数的准确性是粉末成形数值模拟成功的关键因素。采用修正的Drucker-Prager Cap模型对金属粉末压制成形过程进行模拟，基于ABAQUS-MATLAB联合仿真平台，利用复合形优化算法，结合普通模压实验验证，以数值模拟与实验压制力数据的差异性形成目标函数，对其进行最小化，获取本构模型参数。采用材料参数联合反演优化计算Ag57.6-Cu22.4-Sn10-In10混合金属粉末的本构模型参数。结果表明，采用反演优化方法计算得到的本构模型参数较实验测试结果非常接近，通过粉末成形压制力和相对密度模拟结果与文献实验结果对比，进一步验证联合反演优化方法的可行性。

修正Drucker-Prager Cap模型；反演优化；复合形法；材料参数

为了缩短设计周期、降低产品成本、提高粉末冶金制品的质量，将数值仿真技术引入工艺设计并对粉末成形过程中的缺陷进行预测分析是必然趋势[1]。粉末压制成形数值模拟需要准确的本构模型。目前，基于广义塑性力学建立的本构模型在粉末成形数值模拟方面具有更好的准确性，但由于模型复杂且参数较多，一般需要通过各种压坯强度实验、模压实验以及三轴实验来[2−5]确定本构中的各个参数。

为了快速准确地获取本构模型参数，国内外进行了相关研究，但多集中在岩土力学方向。陈峰[6]提出了一单纯形法与有限元结合的优化反分析程序，以观测点的实测值与计算值建立误差函数作为目标函数，实现围岩蠕变参数反演的全自动化操作。贾善坡等[7]采用单纯形法与有限元联合反演法，以实测点地应力值与计算应力值建立精确惩罚函数误差模型，实现对非线性岩体初始应力场的反演计算。此外，贾善坡[8]提出遗传算法与有限元联合反演法，以测点的实测值与计算值建立误差函数，实现岩土工程中复杂本构模型参数和多场耦合参数的反演。关于粉末成形本构方面的研究较少，HRAIRI等[9]提出反演建模程序，以数值模型预测和实验密度数据的差异性形成目标函数，通过Levenberg-Marquardt法对目标函数进行最小化，得到准确的金属本构模型参数。由于目标函数与密度相关，需要做粉末压坯密度测试，实验操作较为复杂。

本文作者基于ABAQUS与MATLAB联合仿真平台，结合普通模压实验验证，提出一种广义塑性力学模型，即修正的Drucker-Prager Cap模型参数反演优化方法，将实验压制力数据与数值模拟结果之差作为目标函数，采用复合形法进行优化计算。复合形法与单纯形法非常相似，与单纯形法相比，复合形法收敛速度快。最终实现以尽量少而简单的实验操作获取本构模型参数，完成金属粉末成形过程快速、准确模拟。

1 ABAQUS-MATLAB联合仿真优化方法

1.1 修正的Drucker-Prager Cap模型

本模拟中基于一种修正的Drucker-Prager Cap模型[10]对材料参数进行反演优化，如图1所示。该模型被假定为各向同性的，它的屈服面由剪切破坏面(s)、帽子曲面(c)和过渡曲面(t)三段组成。其中，为偏应力；为静水压力(平均应力)；为等效应力；为摩擦角；为内聚力；为偏心距(0.0001≤≤1000)；为形状参数，决定了过渡区的形状；b为压缩屈服平均应力，控制着帽子曲面的大小；a为演化参数，帽子曲面与过渡曲面交点的值。

图1 修正的Drucker-Prager Cap模型示意图

在−空间中，屈服面的表达式分别为

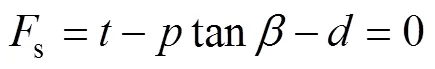
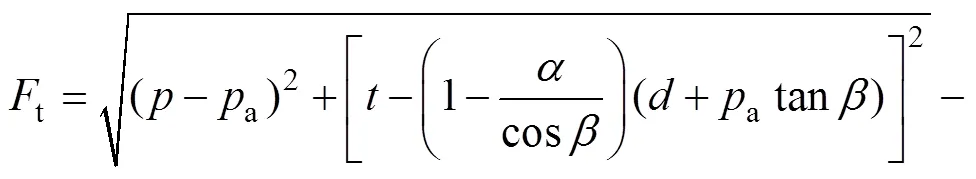
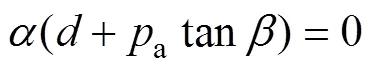
式中：、、、a、b都是与相对密度相关的函数，常用的金属粉末材料参数表达式如表1[11]所示。通常可采用单轴压缩实验和巴西圆盘实验测试压坯强度来确定参数和，且在单轴压缩实验过程中压坯高径比取值范围为2＞/＞2，巴西圆盘实验压坯高径比取值范围为/＜0.25[12]。而偏心距参数一般由三轴实验确定，再结合模压实验数据计算硬化参数a和b[13]。

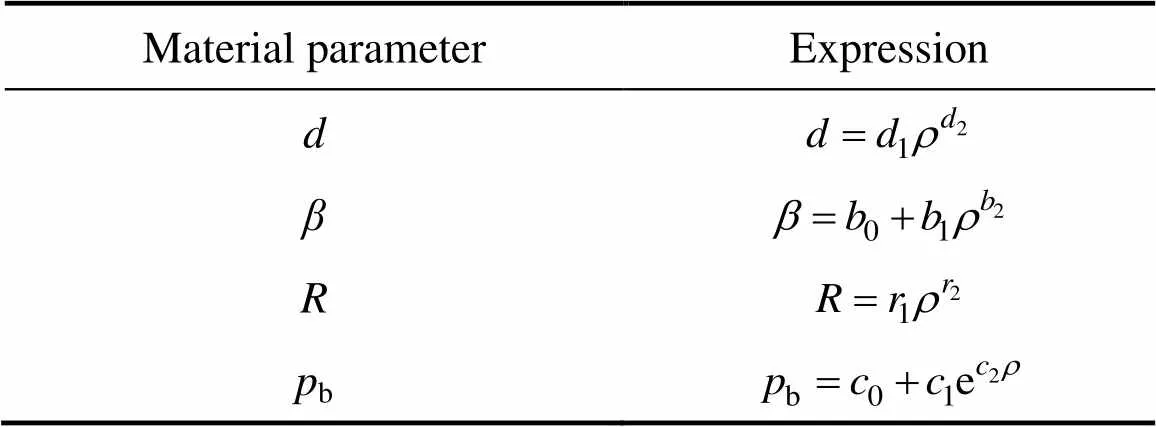
表1 材料参数的表达式

1.2 反演优化方法

不同金属粉末进行压制成形模拟时，至少需要3或4种实验来确定不同相对密度的模型参数。基于此，本文作者结合反演优化方法来确定修正的DPC本构模型参数，以减少大量、繁琐的实验操作。通过普通模压实验，如图2(a)所示，将压制力曲线作为实验验证对比依据，如图2(b)所示，以数值模拟的压制力曲线与实验曲线的差异性最小为优化目标。如式(4) 所示。

图2 模压实验和位移−压制力曲线

如图2(b)所示，冲头压力p采用式(4)编写：

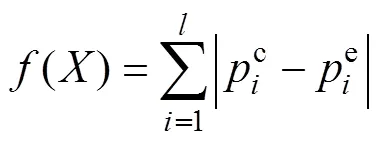
本模拟中主要对内聚力、摩擦角等描述本构模型非弹性行为的材料参数进行优化，需要优化的参数为=(，，，a，b)。由文献[13]中得出，参数a和b与参数、和是相关联的(见式(5)和式(6))。因此，只需要优化参数、和，并结合模压实验测得的轴向应力和位移来确定a和b的取值。参数是常数(0.01~0.05)，本模拟中直接选取参数为0.03。由于优化的参数都是与密度相关的函数，结合表1各参数的函数表达式，最终需要优化的向量为=(1，2，0，1，2，1，2)。

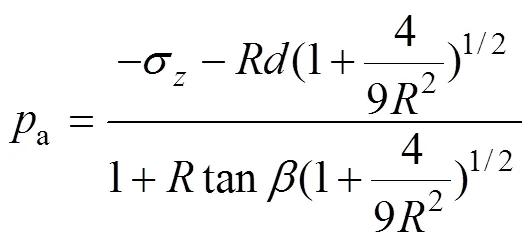
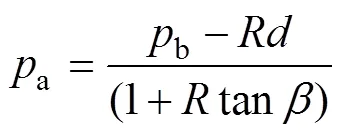
采用复合形法[14−16]对材料参数进行反演优化。使用该法仅需比较目标函数值即可决定搜索方向，算法较简单，对目标函数的要求不苛刻。基本思路为通过构造复合形来求得最优解，新的复合形通过替换旧的复合形中的坏点得到，替换方式为反射、压缩、扩展等几个基本方法，具体步骤如下。

1) 选择复合形的顶点数(+1≤≤2)，在可行域内构成具有个顶点的初始复合形。

2) 分别计算个复合顶点对应的目标函数值，找出最好点L、最坏点H及次坏点G。

3) 计算出去最坏点H以外的(−1)个顶点的中心c。若c为非可行点，则重新确定设计变量的下限和上限值，构造新的初始复合形。

4) 按R=c+(c−H)式来计算反射点R。必要时，改变反射系数直到反射成功。

a) 若(R)＜(c)，采用扩张方法，按E=R+(R−c)找到更好的新点E。若E为可行点且(E)＜(R)，则扩张成功，用E取代R构成新的复合形。否则扩张失败，用原反射点R取代H，构成新的复合形。

b) 若(R)＜(c)，在c以内，采用收缩的方法，按x=H+(c−H)式寻找较好的新点x。若(x)＜(H)，则收缩成功，用x取代H，构成新的复合形。

在应用ABAQUS及二次开发平台模拟金属粉末压制成形过程的基础上，结合MATLAB中的复合形调优算法，编制出一套材料参数反演优化程序。具体流程图如图3所示。

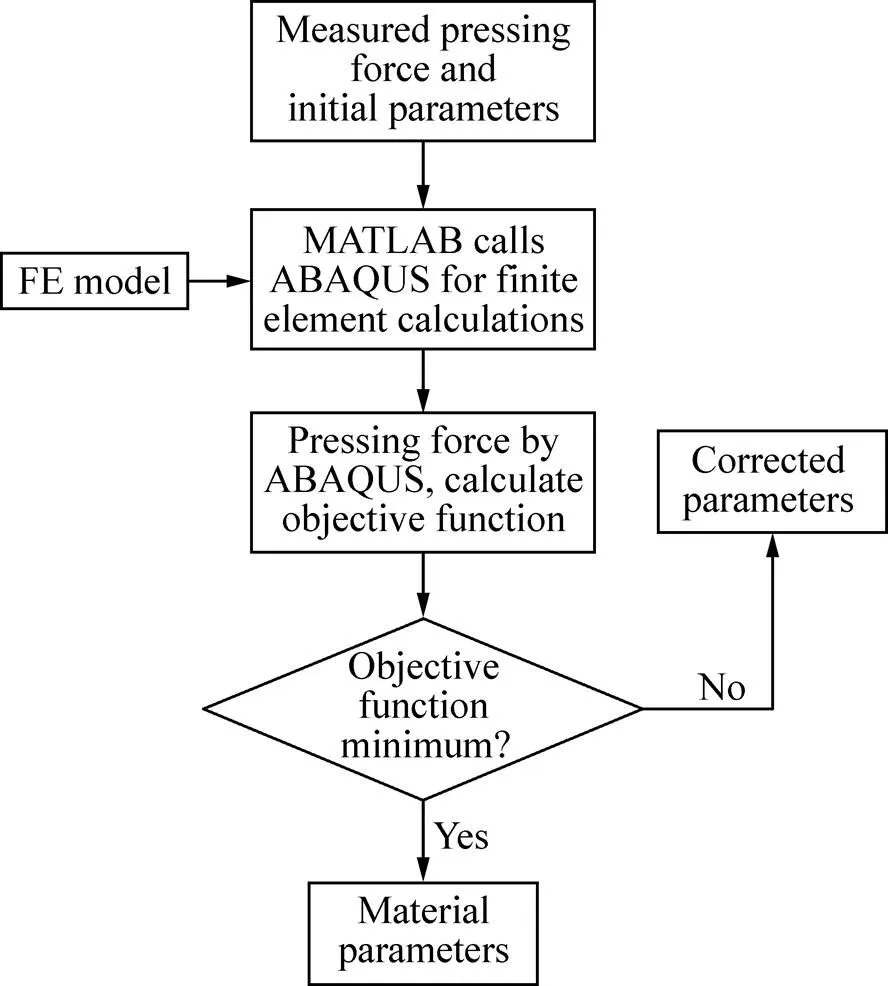
图3 材料参数反演优流程图

2 混合金属粉末本构模型参数反演计算

本模拟中对Ag57.6-Cu22.4-Sn10-In10混合金属粉末[17]的材料参数进行反演优化。模压实验采用单向压制方式，上模冲向下移动压制粉末，下模冲保持静止不动。粉末初始相对密度0=0.42，填粉高度0=15.82 mm，压坯直径为=10 mm，最终压坯高度=7.6 mm。为了提高计算效率，采用轴对称单元进行建模，有限元模型如图4所示，粉末设为变形连续体，阴模和上、下模冲设为刚体，由于实验中进行了模壁润滑，摩擦因数设为0.08。弹性参数中，弹性模量与泊松比的取值如表2所示。

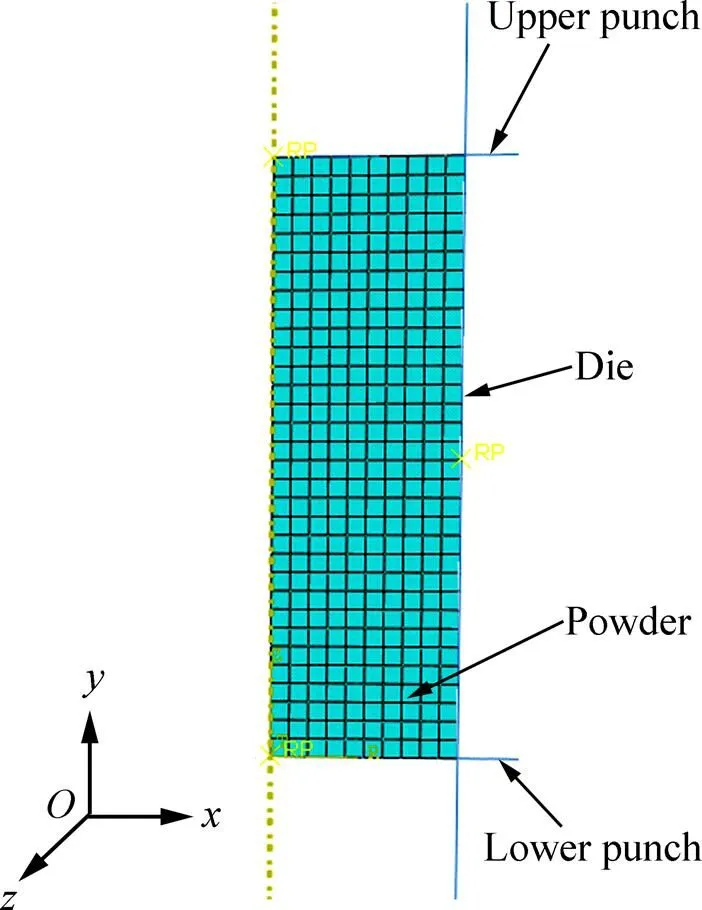
图4 轴对称有限元模型示意图

将铁基粉Distaloy AE的材料参数作为向量初始值，如表4所示，对Ag57.6-Cu22.4-Sn10-In10混合金属粉末的本构参数进行反演优化。目标函数如式(4)所示，约束条件：1＞0，2＞0，0＞0，1＜0，2＞0，1＞0，2＞0。

表2 弹性参数表达式

3 结果与讨论

通过MATLAB与ABAQUS联合反演优化，最终得出参数，和的反演优化结果，如表3所示。将优后的参数与实验获得的参数对比，如图5所示。由图5(a)、(b)、(c)可知，反演优化后的参数、和曲线与实验获得数据曲线基本吻合。图5(d)所示为反演优化参数、和后通过式(5)和(6)计算得出的参数b与实验获取参数b的对比，虽然在高密度区域反演优化数值略大，但变化趋势基本一致。由此说明，该反演优化方法获得的本构模型参数具有较高的准确性。进而将本构模型参数、和对于反演优化结果的灵敏度进行分析，计算式(7)所示：

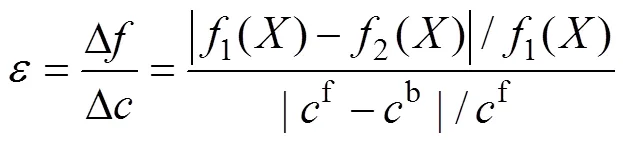
式中：1()表示参数为初始值时的制力与实验压制力之差；2()表示优化后的压制力与实验压制力之差；f表示参数的初始值；b表示参数的优化值。

计算结果如图6所示，其中参数、和灵敏度之和分别为2.19、9.85和2.67，说明其对反演优化结果的贡献率基本在同一水平，虽然参数的灵敏度较和要大些，但这与参数预设初始值和真实值接近有关，由于大部分金属粉末材料的摩擦角都在70°左右[11]。

图7所示为反演优化前后采用Ag57.6-Cu22.4- Sn10-In10混合金属粉末压制模拟得到的压制力曲线与实验曲线的对比关系，结果表明，优化后的曲线与实验曲线变化趋势基本一致。说明优化后的模型的材料参数对Ag57.6-Cu22.4-Sn10-In10混合金属粉的压制行为进行了准确描述。

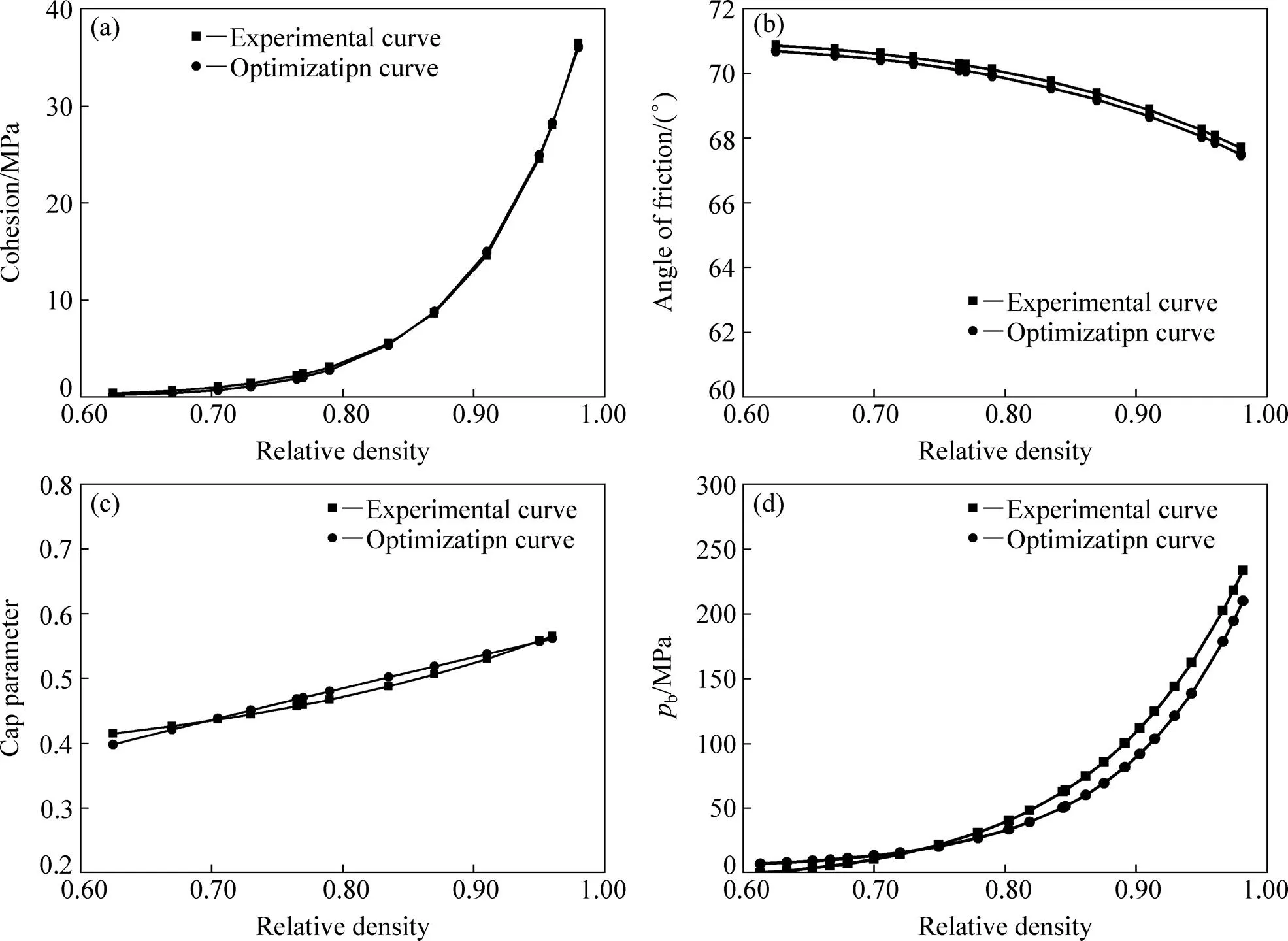
图5 优化后的参数与实验获取的参数对比

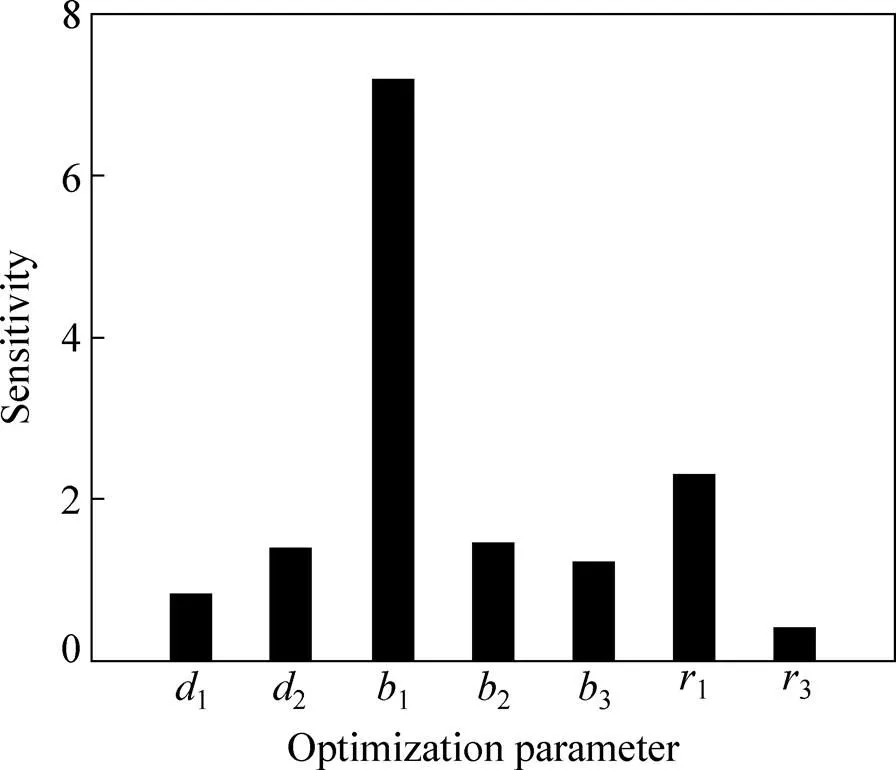
图6 优化参数关于压制力的灵敏度

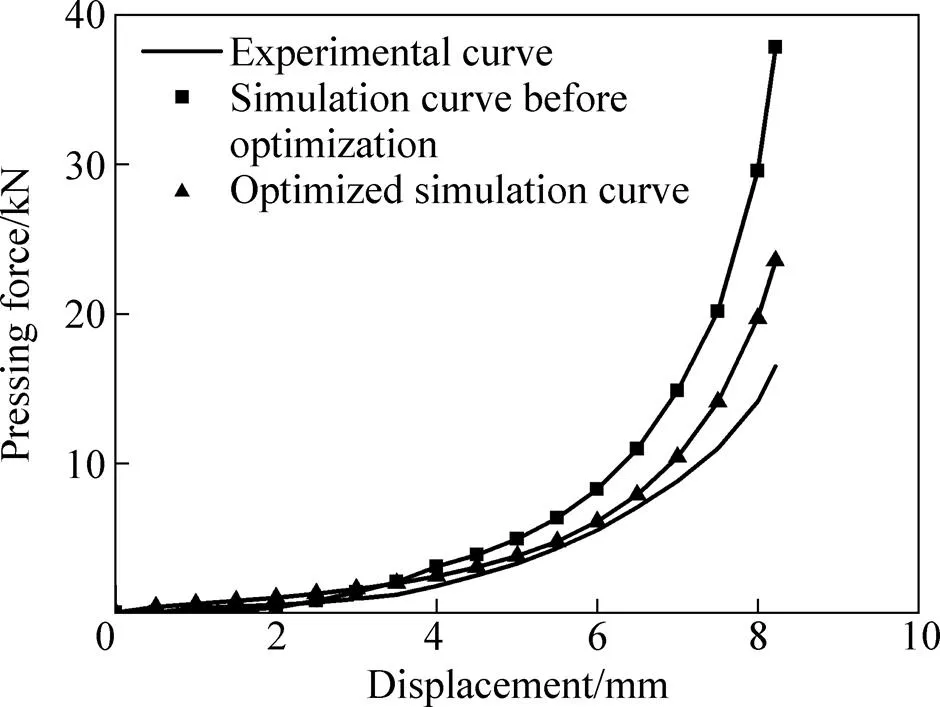
图7 优化前后的压制力与实验的压制力的对比

图8所示为反演优化后相对密度分布与文献模拟结果对比。由图8可以看出，在与模具接触的右上方区域相对密度较高，而与模具接触的右下方区域相对密度较低，造成这一现象的原因是模具和粉末之间的摩擦作用。从图8观察到，在粉末压坯中心的相对密度几乎是均匀分布的，其值为0.8732，这是与粉末压制实验的最终相对密度0.875是一致的。通过与文献压坯相对密度分布模拟结果对比，进一步验证了上述反演优化方法的可行性。

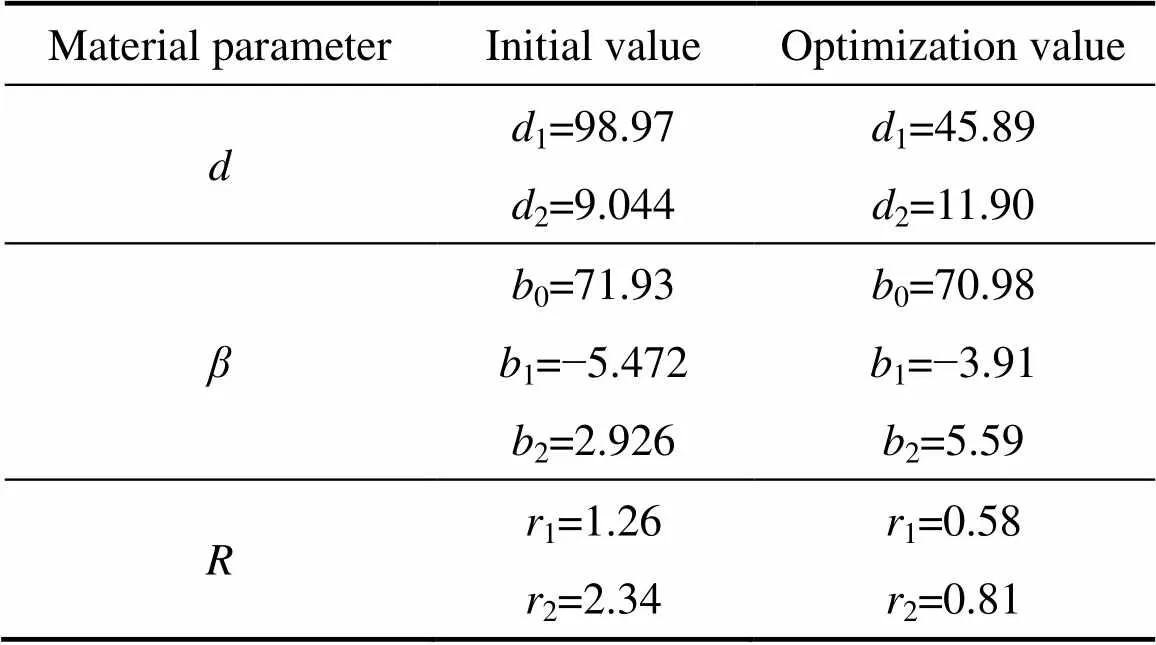
表3 反演模型参数初始值及反演结果

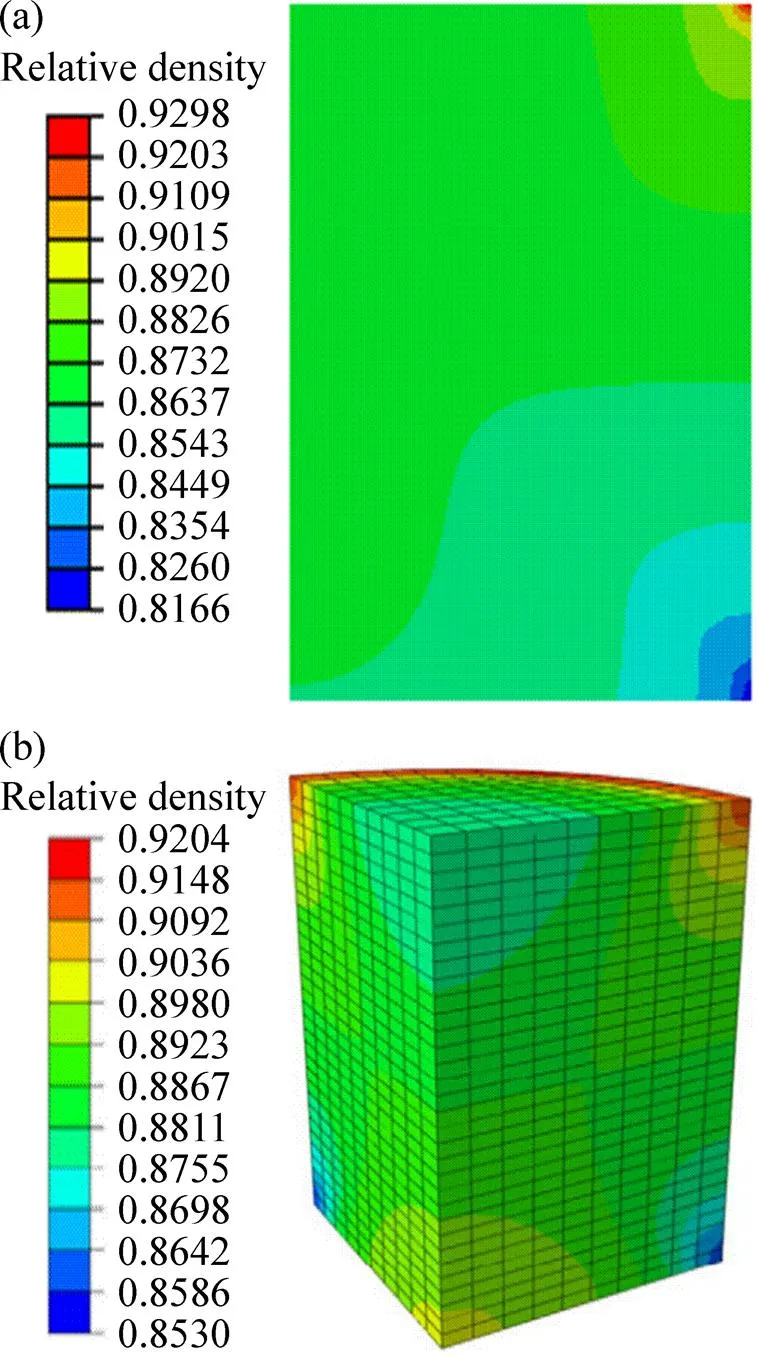
图8 优化后相对密度分布

4 结论

1) 该MATLAB与ABAQUS联合仿真反演优化方法是一种用于确定金属粉末成形本构模型参数的可行性方法。该方法基于ABAQUS与MATLAB联合仿真平台，结合普通模压实验验证，采用复合形法对修正的Drucker-Prager Cap模型进行本构参数反演优化计算，代替一些昂贵而复杂的实验，快速准确地获得本构参数、、和b。

2) 通过对Ag57.6-Cu22.4-Sn10-In10混合金属粉末材料参数的优化结果可以看出，反演优化后的参数、和曲线与实验获得的曲线基本吻合，且各个参数对优化结果的贡献率基本在同一水平。采用反演优化参数、和结合推导式计算得出的参数b与实验得到的b曲线亦基本吻合。且反演优化后模拟得到的压制力曲线与实验曲线变化趋势基本一致。此外，粉末成形相对密度分布与文献模拟结果基本相同，进一步表明该方法的可行性与准确性。

3) 对金属粉末成形本构模型参数反演优化方法的研究，可进一步推广到非金属材料的成形模拟参数的快速获取，对于实际生产中的工艺优化以及缺陷预测具有很强的实用性。

[1] 董林峰. 粉末金属成形过程计算机仿真与缺陷预测[M]. 北京: 冶金工业出版社, 2011: 1−2. DONG Lin-feng. Computer simulation and defect prediction of powder metal forming process[M]. Beijing: Metallurgical Industry Press, 2011: 1−2.

[2] HOFSTETTER G, SIMO J C, TAYLOR R L. A modified Cap model: Closest point solution algorithms[J]. Comput Struct, 1993, 46(2): 203−214.

[3] CHTOUROU H, GAKWAYA A, GUILLOT M. Modeling of the metal powder compaction process using the cap model. Part I: Experimental material characterization and validation[J]. Int J Solids Struct, 2002, 39(4): 1059−1075.

[4] PAVIER E, DOREMUS P. Mechanical behaviour of a lubricated iron powder[J]. Metal Powder Report, 1996, 52(10): 43.

[5] MOSBAH P. Modeling and experimental study of metal powders behaviour during compaction in closed die[D]. Grenoble: University Joseph Fourier-Grenoble I, 1995.

[6] 陈 峰. 基于单纯形—有限元耦合算法的隧道围岩蠕变参数反演[J]. 国防交通工程与技术, 2015, 13(2): 27−31. CHEN Feng. Inversion of creep parameters of tunnel surrounding rock based on simplex finite element coupling algorithm[J]. Traffic Engineering and Technology for National Defense, 2015, 13(2): 27−31.

[7] 贾善坡, 陈卫忠, 谭贤君, 吕森鹏. 大岗山水电站地下厂房区初始地应力场Nelder-Mead优化反演研究[J]. 岩土力学, 2008, 29(9): 2341−2349. JIA Shan-po, CHEN Wei-zhong, TAN Xian-jun, LÜ Sen-peng.Nelder-Mead algorithm for inversion analysis of in-situ stress field of underground powerhouse area of Dagangshan Hydropower Station[J]. Rock and Soil Mechanics, 2008, 29(9): 2341−2349.

[8] 贾善坡. 基于遗传算法的岩土力学参数反演及其在ABAQUS 中的实现[J]. 水文地质工程地质, 2012, 39(1): 31−35. JIA Shan-po.Inversion of geotechnical parameters based on genetic algorithm and its implementation in ABAQUS[J].Hydrogeology and Engineering Geology, 2012, 39(1): 31−35.

[9] HRAIRI M, CHTOUROU H, GAKWAYA A, GUILLOT M. Modeling the powder compaction process using the finite element method and inverse optimization[J]. Int J Adv Manuf Technol, 2011, 56(5): 631−647.

[10] SIMULIA Inc. Abaqus 6.9.1 theory manual [M]. Providence, USA: Software Corporation, 2009: 115−120.

[11] BREWIN P R, COUBE O, DOREMUS P, TWEED J H. Modelling of powder die compaction[M].Engineering Materials & Processes, 1998.

[12] DOREMUS P, TOUSSAINT F, ALVAIN O. Simple test standard procedure for the characterization of green compacted powder in recent developments in computer modeling of powder metallurgy processes[M]. Amsterdam: ISO Press, 2000: 5−8.

[13] ZHOU Rui, ZHANG Lian-hong, HE Bai-yan, LIU Yu-hong. Numerical simulation of residual stress field in green power metallurgy compacts by modified Drucker-Prager Cap model[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(8): 2374−2382.

[14] 王思仁. 复合形法及其应用[J]. 江西水利科技, 1995, 21(2): 93−96. WANG Si-ren.Complex method and its application[J]. Jiangxi Hydraulic Science & Technology, 1995, 21(2): 93−96.

[15] 陈永会, 李海虹, 李志谭. 复合形法解决多维非线性有约束优化问题[J]. 精密制造与自动化, 2002(3): 37−38. CHEN Yong-hui, LI Hai-hong, LI Zhi-tan. Multi dimensional nonlinear constrained optimization problem with complex method[J]. Precision Manufacturing and Automation, 2002(3): 37−38.

[16] 龚 纯, 王正林. 精通MATLAB最优化设计[M]. 北京: 电子工业出版社, 2011: 201−205. GONG Chun, WANG Zheng-lin. Proficient in MATLAB optimization design[M]. Beijing:Electronic Industry Press, 2011: 201−205.

[17] ZHOU Meng-cheng, HUANG Shang-yu, HU Jian-hua, LEI Yu, XIAO Yong, LI Bei, YAN Shi-wei, ZOU Fang-li. A density-dependent modified Drucker-Prager Cap model for die compaction of Ag57.6-Cu22.4-Sn10-In10 mixed metal powders[J]. Powder Technology, 2017, 305: 183−196.

Inversion optimization of constitutive model parameters of metal powder forming based on ABAQUS-MATLAB joint simulation

LI Lu-lu1, ZHOU Rui2, ZHANG Jian-guo1, XIE Dong1, WU Meng-li2

(1. School of Mechanical Engineering, Tianjin University of Science and Technology, Tianjin 300222, China; 2. School of Aeronautical Engineering, Civil Aviation University of China, Tianjin 300300, China)

The accuracy of the constitutive model parameters is a key factor in the numerical simulation of powder forming. The modified Drucker-Prager Cap model was used to simulate the forming process of metal powder. Based on the ABAQUS-MATLAB joint simulation platform, the compound optimization algorithm was combined with the common die compaction test. The objective function was formed based on the discrepancy in force-displacement data between the numerical model prediction and the experiment. The objective function was minimized to obtain the parameters of the constitutive model. The joint inversion of material parameters was used to optimize the parameter calculation of the constitutive model for Ag57.6-Cu22.4-Sn10-In10 mixed metal powder. The results show that the constitutive model parameters calculated by the inversion optimization method are very close to the experimental results. The feasibility of the joint inversion optimization method is further verified by comparing the simulation results of the powder forming compression force and the relative density with the experimental results.

modified Drucker-Prager Cap model; inversion optimization; complex method; material parameter

Project(51505483) supported by the National Natural Science Foundation for Young Scholar; Project (15JCQNJC42900) supported by the Tianjin Natural Science Foundation, China

2017-05-23;

2017-10-10

ZHOU Rui; Tel: +87-13821481662; E-mail: reaterbutter@163.com

10.19476/j.ysxb.1004.0609.2018.07.14

1004-0609(2018)-07-1387-07

TF124.31

A

国家青年科学基金资助项目(51505483)；天津市自然科学基金资助项目(15JCQNJC42900)

2017-05-23；

2017-10-10

周 蕊，讲师，博士；电话：13821481662；E-mail：reaterbutter@163.com

(编辑 龙怀中)