地震动基线漂移校正方法的比较研究

滕浩钧，尹训强，盛 超

（大连大学 土木工程技术研究与开发中心，辽宁 大连 116622）

0 引言

目前，地震反应分析所使用的地震动来源于真实地震动的数据采集和地震动的人工合成。地震动采集的数据大都是以加速度时程的形式给出，而速度和位移时程通常由加速度积分获得。如果不考虑地层断裂、裂缝等因素，在地震结束后，地面运动应该回归初始状态，即地面位移、速度、加速度应该归零。但是，由于地震动采集过程中存在低频仪器噪声、低频环境噪声、加速初始值和速度初始值及人为操作误差等诸多原因，可能导致由积分得到的速度和位移时程在终点时刻非零，即零线漂移。另一方面，在地震动的人工合成计算中，人们往往比较注重对加速度时程的研究，而速度和位移时程仅仅通过地震加速度时程简单的积分运算得到，这也导致速度和位移时程表现漂移现象。国内外学者提出很多校正方法来消除基线漂移，其中包括滤波及低阶多项式曲线拟合，均取得了较为明显的效果。本文将重点研究3种方法，即Jianbo li法、Boyce法和Trujillo法，通过对比研究，提出一种简便可靠的处理方法。

1 3种校正地震动基线漂移方法的原理

为了便于比较研究，首先介绍一下地震动基线漂移现象，然后概述校正地震动基线漂移的Jianbo li法、Boyce法和Trujillo法。由加速度、速度、位移的几何积分关系，在速度、位移初始值均为零的条件下，t时刻的三者关系可以表示为

假设加速度记录在时间段[0,t ]内有N个采样间隔的N + 1个采样值，则上式离散为

1.1 Jianboli法[1]

对比大量的积分位移时程的拟合均值线后，按照位移点在均值线两侧分布均匀和多项式阶数尽可能低的准则，以四阶多项式模拟较好。

假定速度、位移初始值均为零。以四阶多项式模拟位移均值线，如下式，

根据加速度、速度及位移间的积分关系，与上式(3)对应的速度和加速度时程分别为：

1.2 Boyce法[2]

该方法认为加速度纪录一般比实际情况延迟了0.1 s。

假定初始速度不为零，初始位移为零。加速度的均值线用二阶多项式拟合，校正后的加速度时程如下式（6）所示，

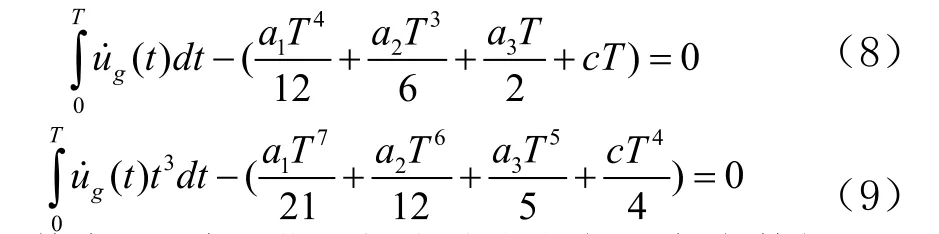
其中，T为周期，解上述方程得出各参数如下，

将参数代入（6）式中得速度时程，对校正后的速度时程积分就可得到位移时程。

1.3 Trujillo法[3]

Trujillo法对基线的校正原理是寻找一组与原加速度记录相近的数据，要求对校正后的加速度时程积分所得的速度时程的末端速度等于零或者接近于零。这一问题也可以用求最小值问题来表述，定义一般情况下的误差如下：

江阴水利信息化一期工程共建设电信和移动4～10 M光纤专线45条、100 M光纤专线7条，并实现与原有省、市防汛专网及江阴市政务网的安全融合。

Trujillo法的递推格式如下：

2 校正方法有效验证

采用3种方法对人工地震动A进行校正，地震动A的地震特性t=20 s，T/s=0.01 s，加速度峰值为，加速度时程与位移时程如图1、图2所示：

图1 加速度时程曲线图

图2 未校正位移曲线图

利用Trujillo法，由递推关系式可得校正后加速度、速度及位移，其中参数的选取。

图3 不同工况下地震动校正后位移时程曲线

经3种方法校正后，得到速度时程如图4所示，3种方法校正后，终点时刻速度为零，得到位移时程如图5所示，终点时刻位移为零，通过校正很好的消除了速度和位移的漂移[4]。3种方法对地震动A都有一个很好的校正。

图4 3种方法校正后的速度时程

图5 3种方法校正后的位移时程

频谱特性如图6和图7所示。图6表示阻尼比为5%的绝对加速度反应谱对比。从图可以得出，地震动A经过3种方法校正后的绝对加速度反应谱没有什么变化。图7为加速傅里叶幅值谱比较图，由于傅里叶幅值对称分布，因此选取一般进行对比，通过幅值谱比较图可看出傅里叶幅值谱s除了长周期略有偏差，其他几乎没有什么变化。由此可见，经过3种方法校正的地震动，依旧保持校正前地震加速度的特性。

图6 加速度反应谱比较图

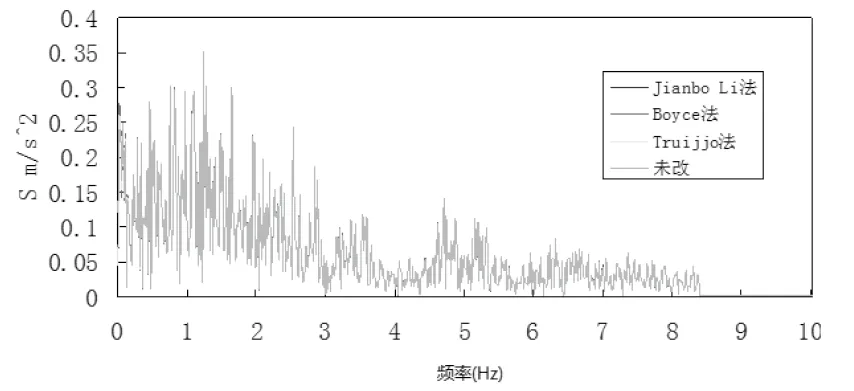
图7 加速度傅里叶幅值谱比较图

3 算例

本例取1940年的El Centro地震动，图8为原加速度时程，图9为未校正位移时程，用Jianbo li法、Boyce法和Trujillo法对El Centro地震动的校正如下：

利用Trujillo法，由递推关系式得校正后加速度、速度及位移，其中参数的选取为。通过3种方法校正后，得到速度时程和位移时程如图9、图10所示。

由图8、图9可看出El Centro地震动的未校正积分位移时程，漂移现象比较显著。对于校正后的速度、位移时程如图10、11所示，三种方法校正后终点时刻速度以及终点时刻位移都归零，但是Jianbo Li法和Boyce法校正效果显著，计算方便简捷，Trujillo法参数选取不明确，且过程较繁，不好确定。但3种校正方法均能较好的消除对原始加速度时程积分得到的位移时程中出现的漂移现象，改善加速度记录的积分特性，并且校正后加速度时程变动较小。工程应用建议使用Jianbo li法或Boyce法。

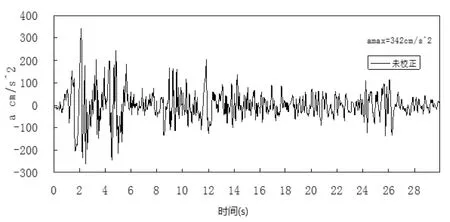
图8 El Centro地震动加速度时程

图9 未校正地震动位移时程

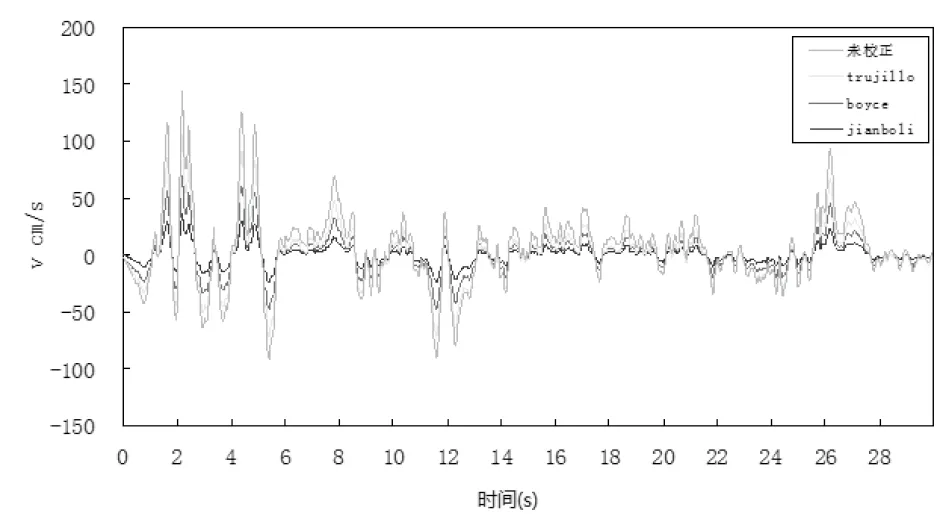
图10 校正后速度时程

图11 校正后位移时程

4 结论与展望

通过对3种校正方法的对比分析，可以得出:

（1）3种校正方法都能较好的消除对原始加速度时程积分得到的位移时程中出现的漂移现象，改善了加速度记录的积分特性，3种方法校正后的地震加速度时程的频谱特性几乎没有发生变化，同时也保证了地震加速度峰值几乎没有改变。

（2）Jianbo Li法和 Boyce法原理简单[5],较易实现。Trujillo法过程较繁，参数 的取值对结果的影响并不是最主要的，但要进行多次试算，同一取值并不适用于任何一条地震动，工程应用中建议使用Jianbo Li法和Boyce法，

（3）所有的校正方法都是基于不考虑地面永久变形的条件下，若能考虑地面永久变形条件下校正地震动将是科技的进步。