近红外光谱法测量喷气燃料防冰添加剂 含量的实验研究

王 烨，郭忠烈，王 立，孟凡芹

(1.空军勤务学院研究生大队，江苏 徐州 221000；2.空军勤务学院军需与燃料系，江苏 徐州 221000)

防冰添加剂是喷气燃料常用的添加剂之一，其作用是与燃料中因外界温度降低而析出的游离水生成低凝点的混合物，防止形成冰晶堵塞飞机燃油系统过滤器[1-3]。根据GB 6537—2006规定，我国使用的乙二醇甲醚防冰剂在加注量0.1%～0.15%(体积分数)范围之内可以有效降低飞机燃油系统结冰的风险[4-6]。因此，防冰添加剂的含量是喷气燃料的一项重要检测指标。

喷气燃料防冰添加剂含量的测定方法包括冰点法、折光计法和碘量法。其原理都是先利用水抽提试样中的防冰剂，然后分别根据防冰剂水溶液的低温性能、光谱响应或化学反应性能来测定防冰剂含量[7]。以上测试方法耗时久、操作过程复杂，且无法连续测量。因此，有必要开发一种快速、简便且测量结果准确的方法来检测喷气燃料中的防冰剂浓度。

当前，近红外光谱分析技术凭借其快速、精确、高效等优势已被人们认识和接受，在农业、医药、石油化工、生物科学等领域都有成功的应用。本研究基于近红外吸收光谱建立喷气燃料防冰添加剂含量的预测模型，以期找到一种快速、可靠、高灵敏度的检测方法。

1 实验部分

1.1 主要仪器和试剂

FN711M型傅里叶变换近红外光谱仪，杭州赛曼科技有限公司；手动移液器，大龙兴创实验仪器有限公司。

3号喷气燃料；乙二醇甲醚(浓度99%)，萨恩化学技术上海有限公司；石油醚、蒸馏水等。

1.2 实验方案

利用手动移液器配制出5个不同防冰添加剂浓度的喷气燃料试样，用FN711M型傅里叶变换近红外光谱仪对每个试样进行近红外光谱分析。具体试验参数设为：测量波长范围为1 250～2 500 nm，仪器扫描次数为10次，仪器分辨率为8 nm。根据GB 6537—2006规定，我国防冰添加剂加注量为0.1%～0.15%(体积分数)。考虑到现实测量的需要，实验所选取的5个防冰剂浓度为：0.051%、0.10%、0.159%、0.197%和0.243%。

1.3 数据预处理

为了减少偶然因素对结果的影响，对5个浓度的试样分别进行3次近红外光谱测量，采用Excel软件计算平均值并作为该浓度下的近红外吸收光谱。在MATLAB软件中绘出其图像，见图1～图3。

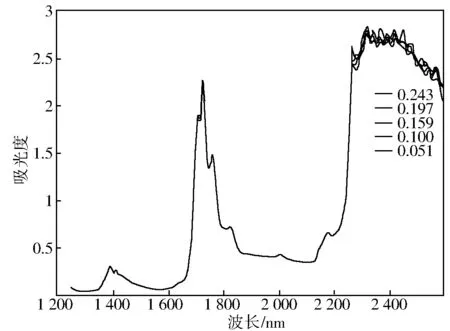
图1 不同防冰剂浓度的喷气燃料近红外吸收光谱

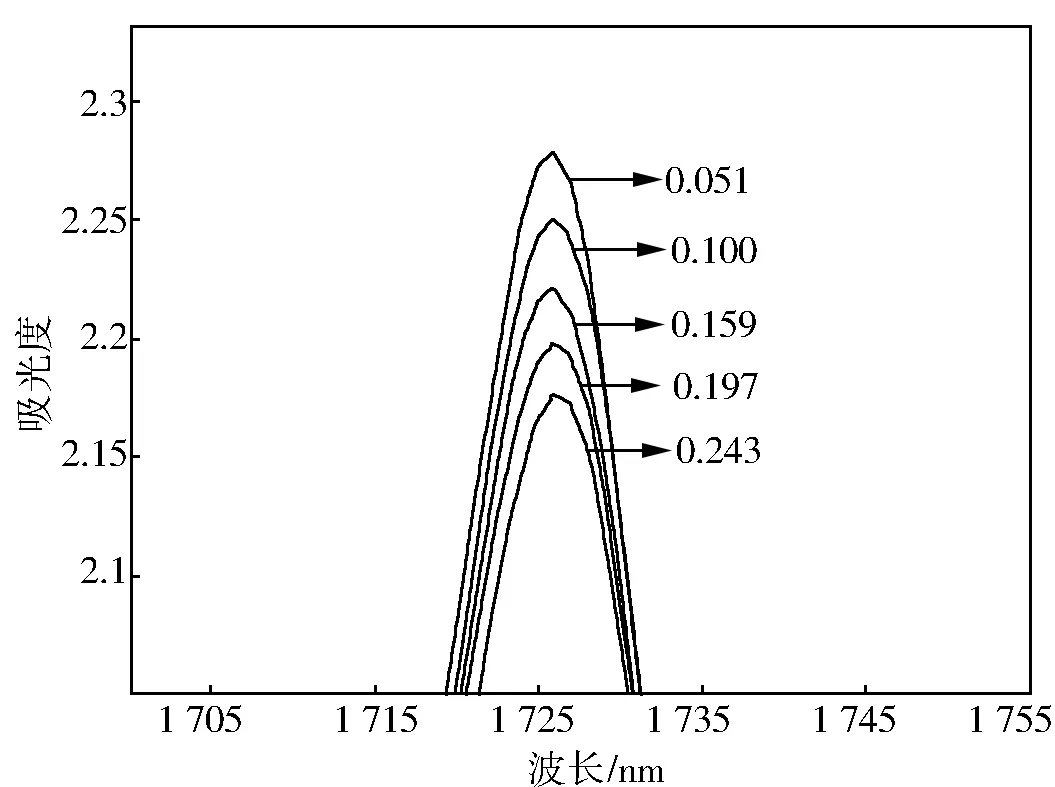
图2 1 726 nm处谱线

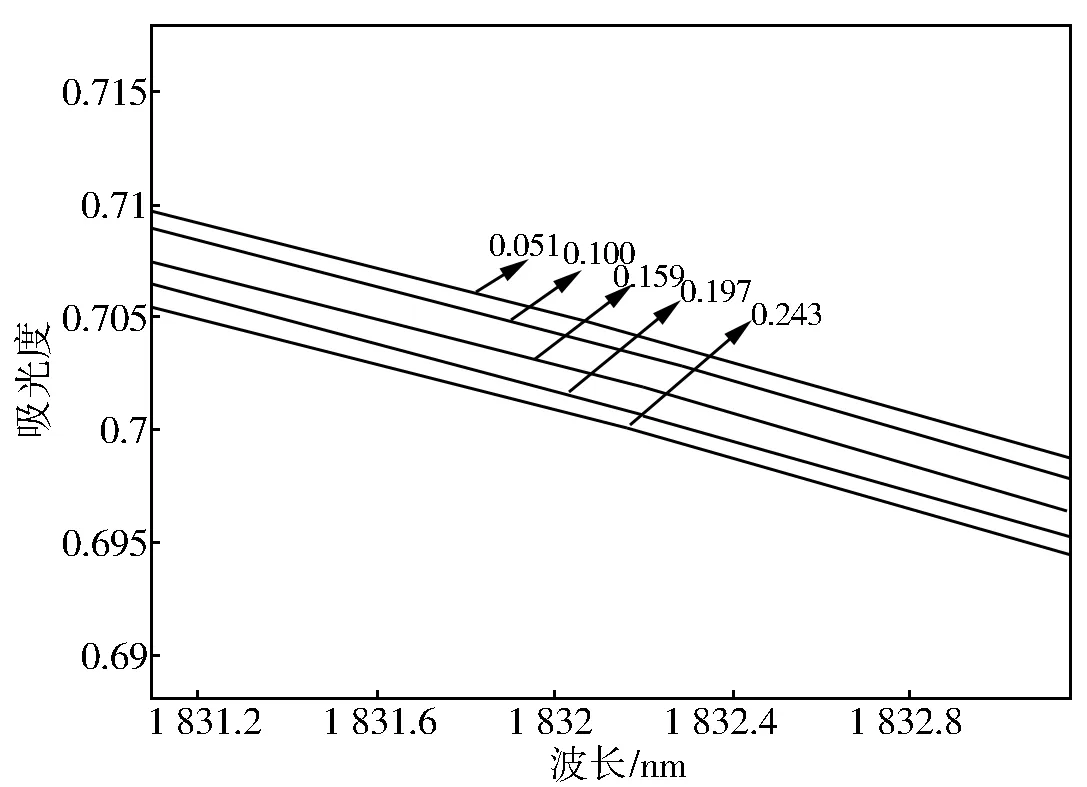
图3 1 832 nm处谱线

2 结果与讨论

2.1 一元线性回归模型的建立

根据实验所得的吸收光谱图，在波长为1 726 nm时，达到一个吸收峰，此时的吸光度如表1所示。

表1 1 726 nm吸收光谱数据

建立一元线性回归模型：

y=b0+b1x

式中，y为防冰剂浓度，x为试样在波长为1 726 nm处的吸光度。

利用数学建模软件MATLAB计算，其输出结果为：b0=4.263 8，b1=-1.852 8，因此，利用一元线性回归方法建立的模型为：

y=4.263 8-1.852 8x

该模型对实验的5个浓度预测结果与真实结果之间关系如表2、图4所示：

表2 一元线性回归模型预测值与实际值

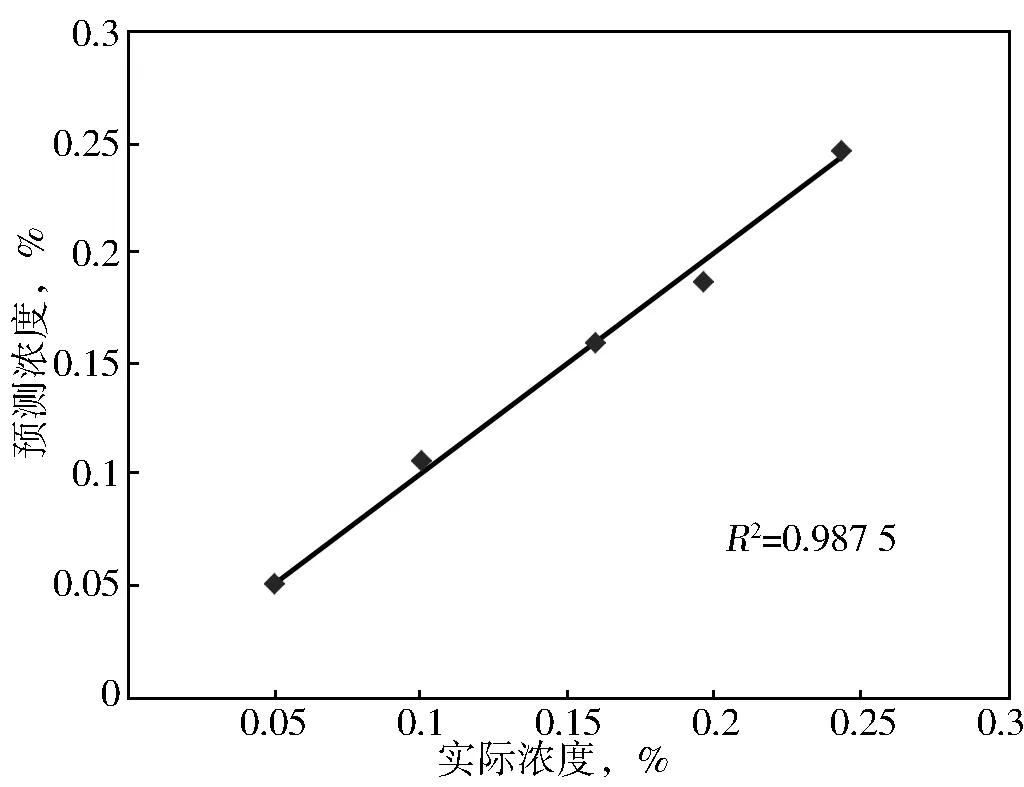
图4 预测浓度与实际浓度相关图Ⅰ

2.2 多元线性回归模型的建立

由于一元线性回归模型只选取了一个波长处的数据，容易产生误差，因此可以采用多元线性回归方法建立模型，增加模型的稳定性。

根据光谱图，选取3个吸收峰的最高点所对应的波长为1 338、1 726、1 830 nm处的吸光度，进行回归分析。其吸收值如表3所示：

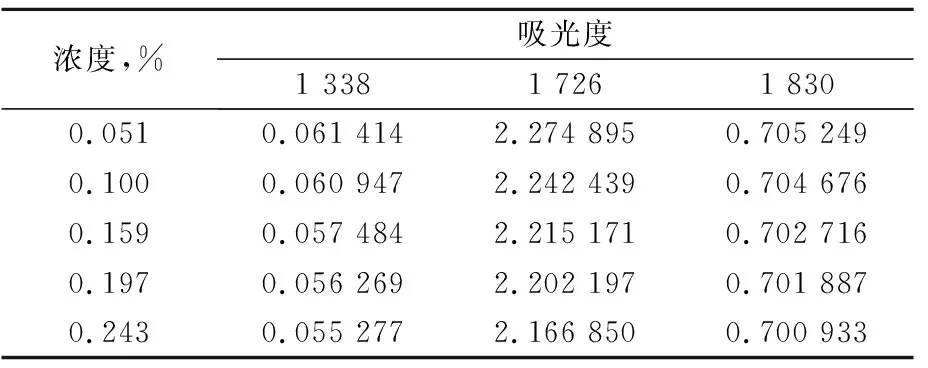
表3 1 338、1 726、1 830 nm吸收光谱数据

假设浓度与吸光度之间存在多元线性关系为：

y=b0+b1x1+b2x2+b3x3

式中，y为防冰剂浓度，x1为试样在波长1 338 nm处的吸光度，x2为试样在波长1 726 nm处的吸光度，x3为试样在波长1 830 nm处的吸光度。

利用MATLAB数学建模软件计算，其输出结果为：b0=18.941 2；b1=-0.958 4；b2=-23.892；b3=2.317 6，因此，得到多元线性回归模型为：

y=18.941 2+2.317 6x1-0.958 4x2-23.892x3

该模型对实验的5个浓度预测结果与真实结果之间关系如表4、图5所示：

表4 元线性回归模型预测值与实际值

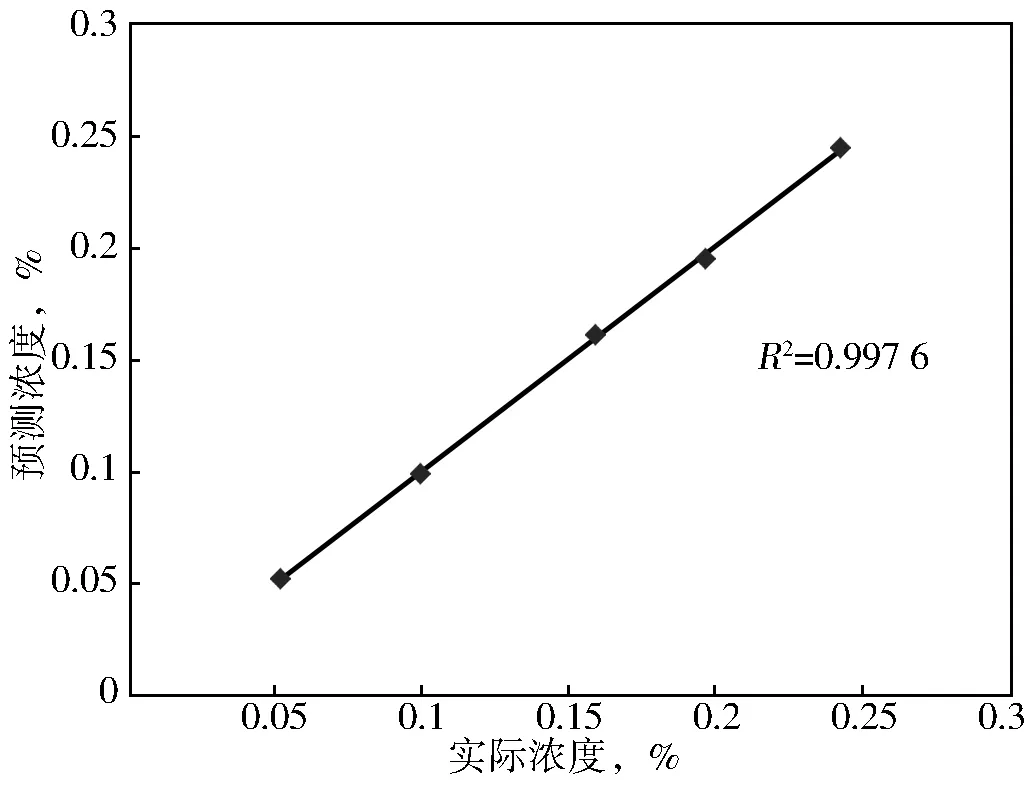
图5 预测浓度与实际浓度相关图Ⅱ

2.3 主成分回归模型的建立

多元线性回归法建立模型相比一元线性回归模型，其对光谱数据的利用率和模型的稳定性都有所提高，但受限于模型的维数，只是选取了少量几个光谱数据，而没有有效利用光谱中的其他数据信息。主成分回归模型可以利用全光谱数据，建立更为有效的模型。

根据光谱图，选取图谱中具有分辨度较高的80个波长处的光谱数据，得到光谱矩阵X5×80，利用MATLAB进行主成分分析。对光谱矩阵求其协方差矩阵

B=XTX

式中，XT为X的转置；对矩阵B求特征值与特征向量，调用函数：

[P，R]=eig(B)

得到特征值构成的对角矩阵R和对应的特征向量矩阵P；观察所有特征值，其中最大的特征值λ=668.4，其贡献率大于95%，其余特征值相对太小，因此选取该主成分作为建模的自变量，其所对应的特征向量为P80×1；

令：

v=X80×1P80×1

得到主成分列向量v，建立主成分与浓度之间的一元线性回归模型为

y=b0+b1v

式中，y为防冰剂浓度，v为主成分，X1×80为选取的80个波长处的吸光度组成的矩阵。计算得到的结果为：b0= 7.596 2，b1=-0.644 1，因此建立的主成分回归模型为：

y=7.596 2-0.644 1v

式中，v为已知的特征向量，因此模型也可表示为：

y=7.596 2-0.644 1X1×80P80×1

该模型对实验的5个浓度预测结果与真实结果之间关系如表5、图6所示:

表5 主成分回归模型预测值与实际值

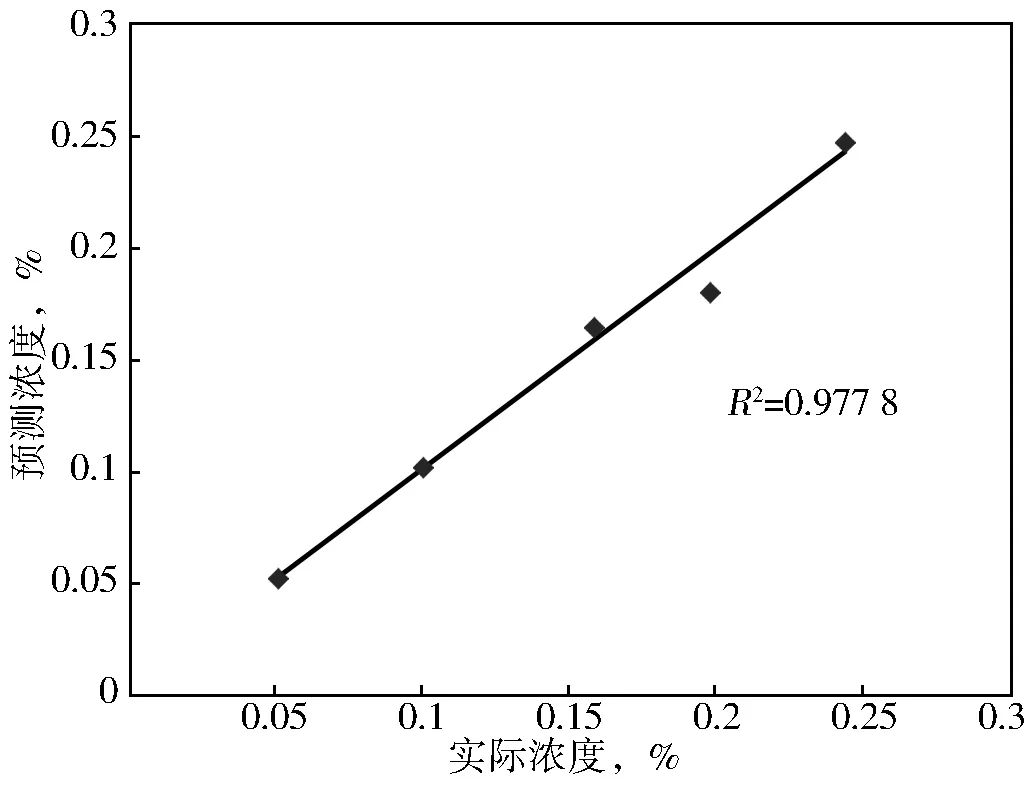
图6 预测浓度与实际浓度相关图Ⅲ

2.4 模型的验证与对比

为了验证模型的准确性，利用实验室材料，配制出3个不同防冰剂浓度的喷气燃料试样，用近红外光谱法对其浓度进行测量，将测量结果与实际结果进行对比。

具体步骤： 1)配制出3个不同浓度的防冰添加剂喷气燃料溶液；2)用光谱仪获取其近红外吸收光谱，并对光谱进行平滑预处理； 3)将光谱数据分别带入3个测量模型，得出测量值；4)将模型得出的结果与已知结果进行比较。

用近红外光谱法测得的浓度与实际浓度的对比如表6所示。

从实验结果可以看出，3个预测模型的绝对误差都小于体积分数0.03%，其中一元线性回归模型的结果较不稳定，最大的绝对误差达到了体积分数0.028%，平均绝对误差为体积分数0.015%，平均相对误差14.3%；多元线性回归模型的测量绝对误差小于0.02%，平均绝对误差为0.012%，平均相对误差为9.5%，相比较一元线性回归模型稳定性有了一定提高；主成分回归模型的测量绝对误差不大于0.01%，平均绝对误差为0.007%，平均相对误差为5.7%；主成分回归模型的预测值最可靠，重现性更好，准确度和灵敏度更高，能够较好地测量防冰剂浓度。

表6 模型测量结果 %

3 结 论

实验利用近红外光谱仪测量了喷气燃料在不同防冰添加剂浓度条件下的吸收光谱，分别建立了3种吸光度与防冰剂浓度之间相关关系的线性回归模型 ，并通过实验验证了模型的准确性。经过对比，发现主成分回归模型对光谱数据利用率高，模型较稳定，预测准确度较好。以上结果表明，利用近红外光谱分析技术对防冰剂浓度的预测是完全可行的。