CSAMT近场校正及全区视电阻率计算在找矿中的应用

周 安，张艳军，苏佳虎

（湖南省核工业地质调查院，湖南 长沙 410011）

可控源音频大地电磁法是在大地电磁法基础上通过引进人工源来提高信号强度，克服其信号微弱的缺点，但人工源的引入也带来了问题，大地电磁法的基础是以平面波为条件，如果人工源发出的电磁信号没有达到平面波条件时，就会出现视电阻率畸变现象，即近场效应。

这是因为CSAMT方法的视电阻率依然沿用大地电磁法中的卡尼亚视电阻率，而视电阻率的定义和适用范围在这两种方法中发生了变化从而导致出现近场效应。往往这种近场产生的非平面波效应可以通过传统的进场校正进行削弱，在一定程度上可以减轻这种非平面波效应，但是很多时候这种校正结果并不可靠，且缺乏灵活性和系统性[1]。

针对这个问题产生的背景和根源，国内外学者提出了全区视电阻率的概念，即针对人工源产生的电磁场重新定义视电阻率，它可以不受波区条件限制，同样适用于过渡区。

本文给出一种计算视电阻率的便利方法，解决方案是以全区视电阻率定义为基础，利用CSAMT的卡尼亚视电阻率作为近场校正的初始值，根据CSAMT所测量的电场分量的全区视电阻率公式进行校正。

本解决方案的优势在于利于卡尼亚视电阻率作为初始值能够快速的得到全区视电阻率值。因此本项目的关键点就是进行CSAMT近场校正，并计算出全区的的视电阻率1-3。

本文的最终目的就是根据理论推导出算法对近场效应进行校正，最后通过实际野外数据的的验证来检验算法的可行性。

1 背景

从原理上讲大地电磁法遵循无源形式的Maxwell方程（齐次方程），电磁波以平面波形式传播（式1所示）。

而引入人工电流源的可控源音频大地电磁法（CSAMT）所遵循有源形式的Maxwell方程（非次齐次方程），电磁波只大离源较远的地方（大于3到5倍趋深度的地方才以平面波形式传播。

从数学上来讲，非齐次方程的通解为齐次方程通解加上非齐次方程的特解。换句话说，我们通过可控源音频大地电磁法(CSAMT)法测得的电磁场可以表示为平面波场与非平面波场之和。我们通过研究非平面波电磁场的特征就可以得到CSAMT视电阻率（阻抗）产生畸变的原因和校正方法。

2 基本原理

平面电磁波条件下的电场和磁场分量为齐次方程的解，可以用阻抗形式来表示为：

其中上标p表示平面波。当有源情况下，电场分量可以表示为：

其中表示非平面波部分，阻抗和视电阻率的畸变主要由这部分引起。此外，由于电磁场不存在磁荷，电场分量和磁场分场可以通过法接第电磁感应定律转换，因此，可能单独研究电场或磁场分量来解决电磁场问题。

根据前人的研究，电磁场在收发距远大于趋肤深度（一般3到5倍的趋肤深度）时场源所产生的电磁波已按平面波形式传播。以柱坐标形式表示的电场分量的球面波和平面波表达式如式5所示：

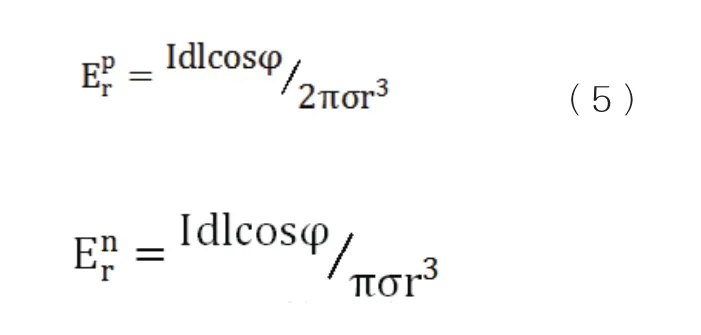
通常标量CSAMT的视电阻率是由观测一对正交的电场和磁场得到，因此，进行视电阻率近场校正时，我们首先，通过得到的视电阻率值计算得到对应的电场值，然后和观测到的电场值进行比较，确定视电阻率的校正参数，最后校正参数进行视电阻率校正[2]。

3 算法流程

本方法需要输入CSAMT法获得的视电阻率，电流归一化后的频率域电场（发送电流和观测到的电场），发送和接收点的位置信息。本算法主要流程如下：

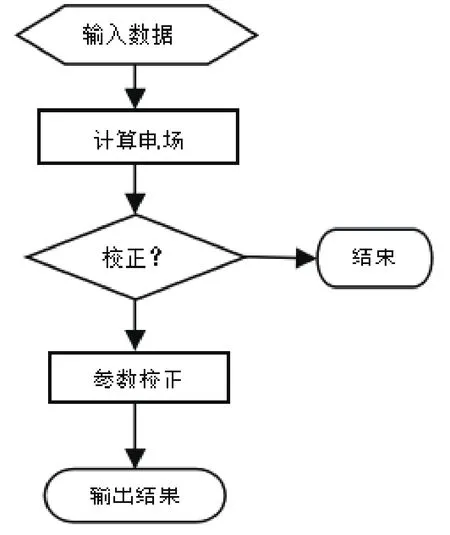
图1 算法流程图

4 算法验证

（1）根据层状大地模型计算真理论视电阻率值，这里可以认为是大地电磁法所测得的视电阻率值。

（2）根据层状大地模型计算CSAMT视电阻率值，认为是CSAMT法实测电阻率值。

（3）根据电场公式（5）计算电场。

（4）对比实测电场，如存在差异认为CSAMT视电阻率需校正。

（5）迭代校正。

（6）利用视电阻率求得相位。

这里我们使用三层模型来验证程序：

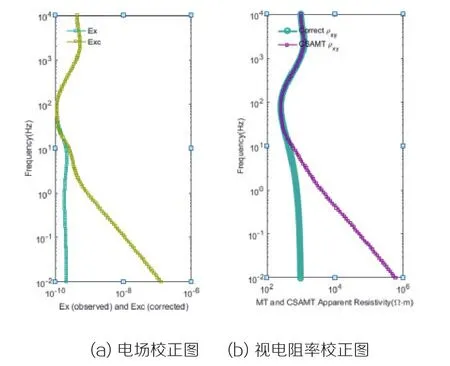
图2 电场及视电阻率校正

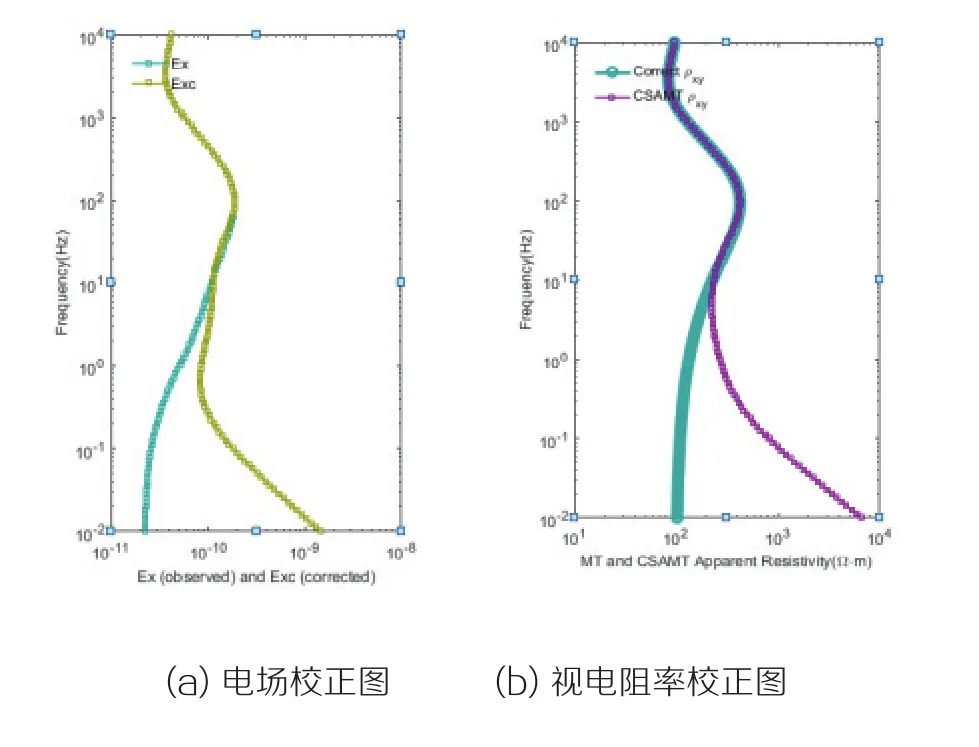
图3 电场及视电阻率校正

通过三层模型证明，该算法对近场效应具有较好的校正效果，利用原始卡尼亚视电阻率作为初始值能够快速的得到全区视电阻率值，对进场效应进行校正是本算法的一大优势。

5 野外数据应用

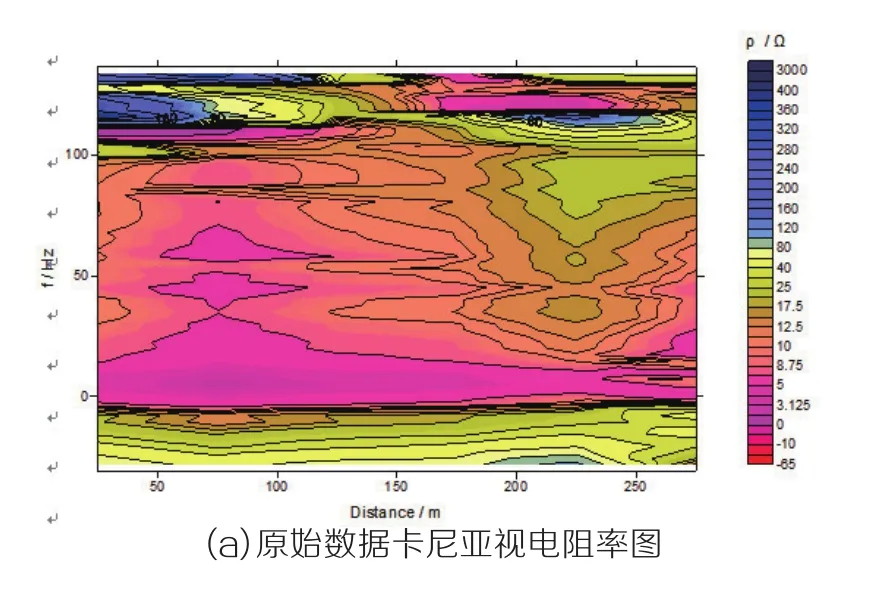
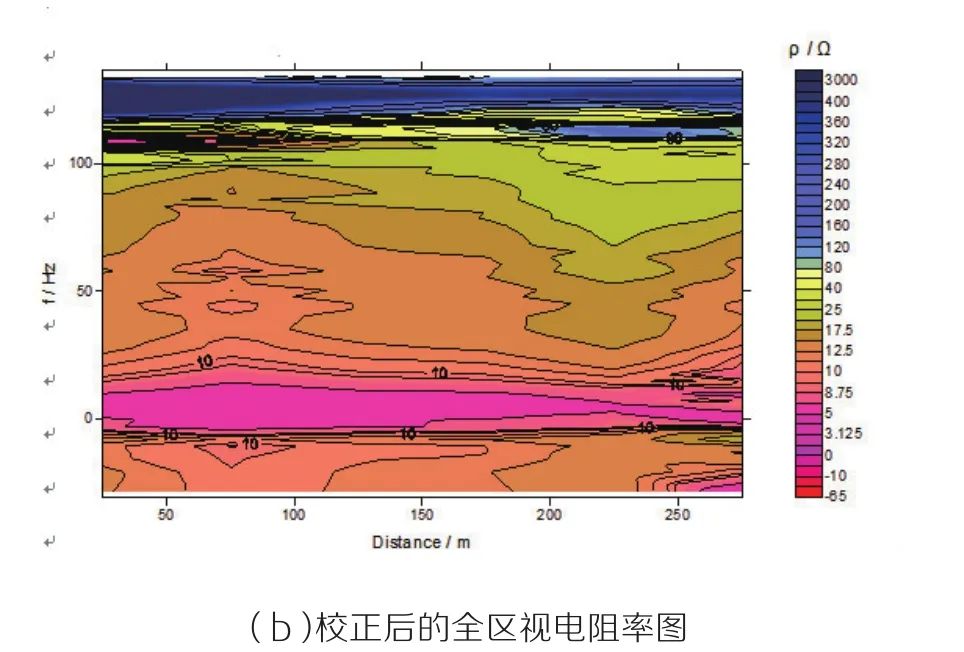
图4 野外数据校正

在湖南某地进行CSAMT勘查，收发距r=6000～8000m，AB=1500～2000m。对其中的一条线数据进行近场校正处理，如图4所示：其中纵坐标表示频率（对频率取1.07的对数），横坐标表示距离。图4（a）中的低频数据进入了近场范围，通过该算法处理进行校正后的效果如图4（b）所示，取得了较好的效果。

6 结论

实验和野外结果表明，采用该算法进行卡尼亚视电阻率近场校正，得到全区视电阻率。

通过比对卡尼亚视电阻率图和全区视电阻率图可以证明采用该算法可以对卡尼亚视电阻率的近场数据进行校正，取得了较好的效果，提高了该方法在找矿中的应用效果。