基于证据理论与多模型结合的模拟电路故障诊断*
2018-08-22宝石,许军
宝 石,许 军
(陆军装甲兵学院,北京 100072)
0 引言
随着电子技术的快速发展以及制造工艺的不断提高,电路系统的复杂程度也在逐渐增加。而模拟电路本身又具有非线性、容差等特点,因此,模拟电路的故障诊断一直都是一个突出的难题。信息融合技术在当前很多领域中都已成功应用,是信息处理的一种重要手段。其中,DS证据理论是由Dempster在1967年提出并在信息融合领域中常用的一种方法,具有很强的处理不确定信息的能力。但其基本概率分配(BPA)是一种人为的判断,盲目性较大,一直以来都是一个很难有效解决的问题。本文将神经网络与支持向量机的初步诊断结果构造成D-S证据理论的基本概率分配(BPA),作为最终决策级融合诊断的证据体。利用两种智能诊断模型的自组织、自学习能力,实现基本概率赋值的客观化,避免了人为操作的不确定性。
BP神经网络又称误差反向传播神经网络,其网络结构一般为三层或三层以上,包括输入层、隐藏层、输出层。传统BP神经网络有很多缺陷,如过饱和,局部最优解等,这些都会对诊断结果产生影响。本文提出一种保留精英个体的免疫遗传算法对BP神经网络进行优化,整合了遗传算法和免疫算法相叠加的部分。种群中个体为神经元之间的权值和隐藏层节点数构成的染色体。依据电压参数规模,一定数量的染色体构成群体。使用免疫算法对群体中个体的多样性进行评价,使用遗传算法对群体进行更新优化,并在优化过程中运用了精英保留策略。
支持向量机(SVM)是在统计学习理论基础上发展起来的基于机构风险最小化的新型学习机器。本文利用MATLAB中libsvm工具箱构建SVM诊断模型,核函数选用径向基函数,并利用一种改进的粒子群算法对其进行参数优化,找出全局最优值。在模拟电路故障诊断中,一般为多分类问题,而支持向量机为二分类硬判决输出。因此,构建“一对一”多分类支持向量机,利用投票法构造每种故障模式的概率输出,并以此作为证据理论的BPA[1]。通过仿真实验,验证了本文提出的综合诊断模型能有效提高故障诊断准确率,相比较与单一诊断模型,能明显降低诊断结果的不确定性。
1 BP神经网络模型构建及其优化
1.1 BP神经网络诊断模型
本文采用3层BP神经网络,输入层节点数对应于输入特征向量的维数,输出层节点数等于故障模式数。期望输出采用n中取1编码方式,隐藏层初始神经元个数根据下式得到,
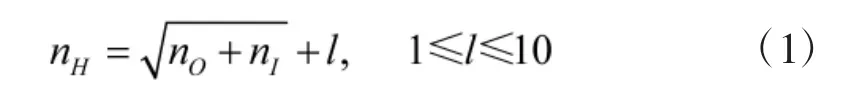
nI,nH,nO依次为输入层,隐藏层,输出层神经元数。
文中隐层与输出层激活函数选取sigmoid函数,神经网络每个节点的输出为[0,1]上的一个数,分别对应每一种故障发生的可能性(故障隶属度),以此输出值构建D-S证据理论的基本概率分配[2]。
1.2 免疫遗传算法优化BP神经网络
传统BP神经网络训练中很容易发生训练停滞、局部最优等问题。基于此本文利用免疫遗传算法对其进行优化,并在算法中设计了一个浓度指标,降低了浓度过高而亲和度较低抗体的繁殖概率,保留真正的精英个体。遗传算法中,神经网络中的权值和隐藏层神经元数被定义成种群的染色体,每个染色体代表一种解,而染色体的数量被定义为种群的数量,即解的数量。染色体则被定义为免疫算法中的抗体。将染色体适应度评价定义为神经网络诊断误差的倒数,并以此诊断误差作为免疫算法中的抗原。实际训练中,通过诊断误差的抗原作用,染色体不断选择、交叉、变异,本文采用轮盘赌选择机制筛选出适应度评价更高的抗体[3]。
染色体的编码主要为抗体chorm,针对问题的解,抗体的编码是以线性实数向量进行编码,以[w1,b1,w2,b2,hiddennum]这一线性形式实数编码整个待解的神经网络。向量元素依次为输入层与隐藏层连接矩阵、隐藏层权重矩阵、隐藏层与输出层连接矩阵、输出层权重矩阵、隐藏层神经元数量。在抗体群更新优化过程中,将神经网络按照输入数据a和输出数据b进行训练,将输入数据a带入到神经网络中,得到诊断数据c。通过诊断数据c和输出数据b进行比对可以得到该染色体对应神经网络的诊断误差,即抗原。

式中,e为诊断误差,i为诊断数据c与输出数据b对应的位数,n为总位数,ci为诊断数据c第i位数值,bi为输出数据b第i位数值。

式中,e'为单位诊断误差,l为输出数据b的总长度。取单位诊断误差的倒数,得到该染色体的适应度值即抗体亲和度。
2 SVM诊断模型构建及其优化
2.1 支持向量机(SVM)诊断模型
传统支持向量机解决的是“二分类问题”,而模拟电路的故障诊断一般都是多分类问题,因此,本文构建了“一对一”多分类支持向量机诊断模型[4],对n个故障类别共构建n(n-1)/2个SVM,每个SVM为一个决策函数。对第r类和第s类,决策函数如下:

故障分类时采用投票法,判断故障x属于r类,则r类票数加1,否则给第s类票数加1。当n(n-1)/2个SVM均分类完毕之后,得到每种故障的总票数V(FS),FS为各个故障模式。本文中,通过将每种故障的得票总数和总票数作比来获取证据理论的基本概率分配(BPA)。

2.2 粒子群算法(PSO)优化支持向量机
粒子群算法的基本思想是通过群体中个体之间的协作和信息共享寻找最优解[5]。系统初始化一组随机粒子(随机解),然后通过迭代找到最优解。在每次迭代中,粒子通过跟踪两个“极值”(pbest,gbest)更新自己,如式(6)和式(7)所示,直到迭代次数达到最大为止。支持向量机模型有很多参数,其中惩罚因子c及核参数滓需要自己取定。针对会有不同c和滓都对应最高准确率的难题,本文对算法进行了改进,选取准确率较高的3组中c最小的那组为最优解。因为过高的惩罚参数c会造成过学习状态,导致最终测试集的准确率不理想。

寻优中通过k-折交叉验证法来评估每一个粒子,随机将数据均分为K部分并计算k倍交叉验证后的平均分类精度作为适应度值,不断进行群体中粒子的更新迭代。优化过程如图1所示。

图1 粒子群优化过程
3 基于DS证据理论的综合诊断模型
D-S证据理论可以处理诊断决策中的不确定性问题,它采用不确定区间表示由于未知信息或信息不全造成的不确定性,已经成为信息融合领域的重要手段。证据理论的最终目的就是在已知辨识框架Θ中所有元素的前提下,判断其中的一个先验未定元素属于辨识框架中某个子集的程度。在模拟电路故障诊断中,即确定各诊断方法对各元件可能发生故障的基本概率分配[6]。
设m1,m2,…,mn是辨识框架Θ上不同证据的基本概率分配,Ai1,Ai2,…,Ain分别为对应的焦元。则本文中证据理论的判定规则如下[7-8]:
1)应当判定具有最大基本概率分配的故障模式为最终故障;
2)判定的故障模式与其他故障模式的BPA之差要大于一定阈值,文中取0.3。
D-S证据理论融合公式为:

综合诊断模型过程如图2所示。

图2 综合诊断模型
首先对待测电路板进行数据采集与预处理,将采集数据进行特征提取,并划分训练数据集与测试数据集。采用小波分解方法对信号进行特征提取,获取各频带内信号特征作为与电路状态对应的故障特征向量。经免疫遗传算法优化的神经网络模型和粒子群算法优化的SVM模型初步诊断后,利用诊断结果进行基本概率分配,最后按照式(8)的规则进行组合、推理及融合,得出最终的故障诊断结论。
4 仿真验证
以下页图3所示的四运放高通滤波器为研究对象,对本文提出的方法进行验证,各元件的标称值图中已标出,节点6和节点12分别为唯一输入、输出点。电阻和电容的元件容差分别为5%和10%。采用Multisim软件对电路进行仿真,利用Matlab进行算法编程与故障诊断。
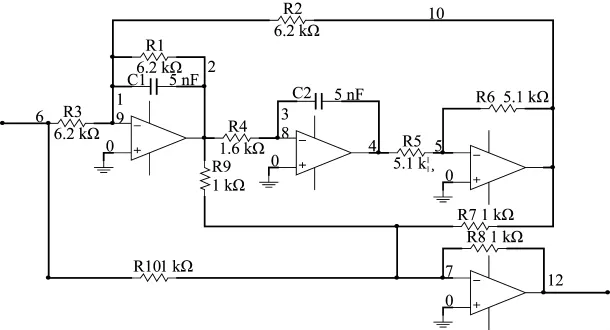
图3 四运放高通滤波器
对待测电路进行灵敏度分析,确定R1,R2,R3,R4,C1,C2对电路性能影响较大,故障设置为以及正常模式共7种。故障值设置为标称值的±50%。选择宽度10滋s,振幅5 V的单脉冲信号作为激励,对每种故障模式进行50次蒙特卡洛分析,其中30次用于训练,20次用于测试。将输出点得到的信号利用db3小波进行5层小波分解,提取各层小波系数的均方根作为特征向量,并对得到的特征向量按照式(9)进行归一化处理,最后送入两种诊断模型进行诊断。

cmax表示样本ci中最大值,cmin表示样本ci中最小值。
根据特征向量维数,神经网络隐藏层神经元个数为7-17,抗体最大长度为245。初步确定神经网络结构为 6-10-7。epochs设为 1 000,goal为 0.01,lr为0.1,trainFcn选为traingdm。免疫遗传算法基本参数如下:种群规模sizepop=20,记忆库容量overbest=5,迭代次数 maxgen=20,交叉概率 pcross=0.5,变异概率pmutation=0.4,多样性评价参数ps=0.95。
首先利用训练数据对神经网络模型进行参数寻优,免疫遗传算法的循环终止条件为最大迭代次数。通过输入训练数据,实现对抗原的识别并产生初始抗体群,同时计算抗体亲和度与浓度。将亲和度较优个体直接保留,剩余个体及浓度过高抗体组成父代群按照上述概率进行选择、交叉、变异之后产生子代群,重复循环直到迭代终止,得到最优参数。将得到的参数带入到BP神经网络中,构建优化后的神经网络模型。通过实验仿真可以发现,每次迭代后神经网络适应度值要远远高于未被优化的神经网络,即诊断误差较小。适应度变化曲线对比如图4所示。
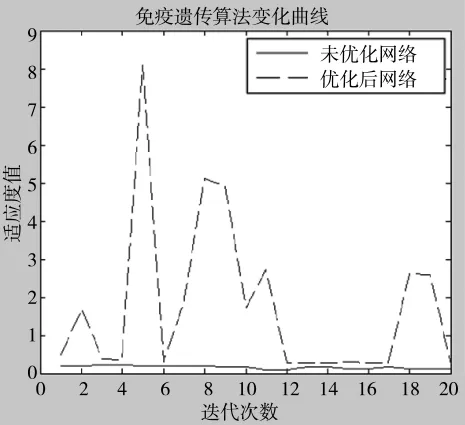
图4 适应度变化曲线
将测试数据分别带入优化的神经网络诊断模型和未优化的神经网络诊断模型,通过20次的迭代训练之后,两者诊断结果正确率如下页表1,可以发现优化后的神经网络对数据的识别能力要远远强于未优化的神经网络。

图5 标准BP神经网络误差曲线

图6 优化后神经网络误差曲线
图5和图6分别为未优化和优化后的BP神经网络误差曲线,未优化BP神经网络经过15次运算后连续6次运算不改变误差值,此时神经网络训练自动结束。验证样本误差为0.15>0.01,无法满足设定的神经网络诊断误差需求,不能准确地诊断出电路故障位置。而优化后的BP神经网络验证样本误差可以达到0.002 1附近,可以满足神经网络对电路板故障诊断的精度要求。
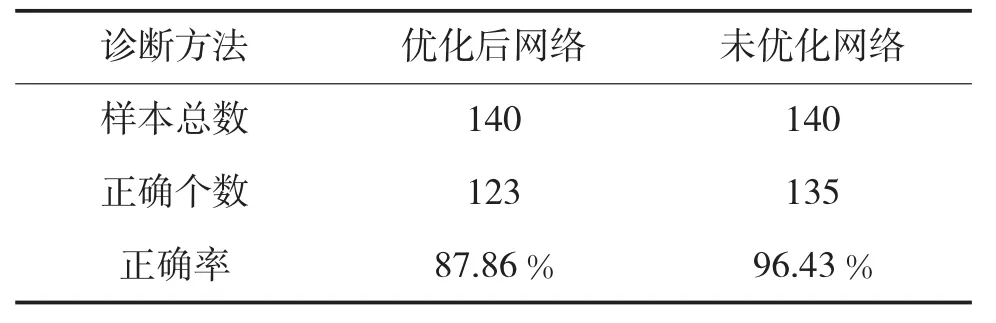
表1 诊断结果正确率对比
在测试样本中选取5组数据,并对其诊断结果进行基本可信度分配,得到证据体E1,如表2所示。

表2 神经网络诊断模型分配的BPA
本文中支持向量机模型选用径向基核函数,粒子群算法初始参数如下:加速度参数c1=1.5,c2=1.7,最大进化数量maxgen=100,种群规模sizepop=20,SVM交叉验证参数K取3。惩罚因子c∈(10-1,102),核函数参数 σ∈(10-2,103)。图7是粒子群算法进行参数寻优的适应度曲线,达到最大终止代数100时,平均适应度值为97.5%。根据改进的最小c原则,选取准确率较高且c较小的最优解组合,得到bestc=17.832 0,bestσ=23.449 3。

图7 粒子群优化适应度曲线

表3 故障编号与期望输出
图8和图9分别是标准SVM与粒子群算法优化后的SVM的测试集分类结果,其中标准SVM分类准确率为92.56%,而优化后SVM分类准确率为97.78%。
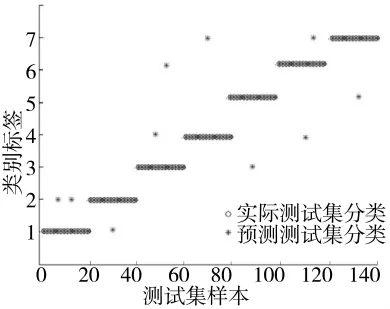
图8 标准SVM测试集分类结果图

图9 粒子群优化SVM测试集分类结果图
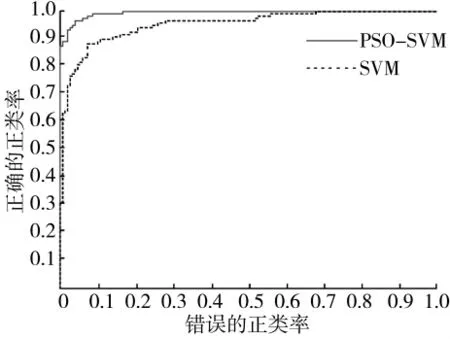
图10 ROC曲线对比图
图10是粒子群优化后的SVM与标准SVM的ROC曲线对比图,曲线越接近左上角,说明该分类模型具有更好的分类性能。从图中也可以看出分类效果明显高于标准。同样取5组测试数据,得到其证据理论基本概率分配如表4,即证据体E2。

表4 SVM诊断模型分配的BPA
按照式(8)对两种诊断模型分配的基本可信度(表2与表4)进行决策层融合诊断,得到最终的各故障的基本概率分配,如下页表5所示,根据判定规则,确定故障元件。
结果分析:因为两种诊断模型各自的诊断机理不同,所以对待每一种故障时敏感度不同,均会产生一定的不确定性和模糊性。如神经网络模型对第3、5组测试样本无法作出准确判断,而支持向量机模型则对第4组样本存在多个类别票数相同的情况,无法正确分类。但经过证据理论的决策层融合诊断后,充分利用了两种诊断模型的诊断信息,可以有效提高每种故障的诊断准确率与精度,避免了单一诊断模型不能全部正确分类的不足,能够准确地定位故障元件。

表5 D-S证据理论融合后的可信度分配结果
5 结论
本文结合DS证据理论、BP神经网络和支持向量机构建了一个综合诊断模型。该模型利用BP神经网络和支持向量机的初步诊断结果进行DS证据理论的基本概率分配(BPA),避免了人为操作带来的盲目性。通过对两种诊断模型的优化,有效解决了各自的缺陷,提高了局部诊断的准确率。经仿真验证,该综合诊断模型能够明显提高每种故障的诊断精度,解决单一诊断模型存在的诊断结果不确定性和模糊性问题,为模拟电路的故障诊断提供了一个新方法。
