网络化火控系统关键事件察觉的SVM方法

2018-08-22王虎跃武云鹏卢志刚

火力与指挥控制 2018年7期

王虎跃，武云鹏，卢志刚，朱锐，张岩

（北方自动控制技术研究所，太原 030006）

0 引言

在装甲车辆分队战斗过程中，对快速变化的态势及时地做出感知响应是装甲车辆网络化火控系统有效决策的必要条件之一。但是，由于装甲车辆网络化火控系统处理的火控信息多样复杂并且多变，在紧张的对抗战斗过程中装甲车辆作战人员面对火控态势图时，可能会出现“信息炫目”，从而迷失于火控信息的快速变化中。装甲车辆分队在战斗对抗过程中，为了降低网络化火控系统操作人员所要关注的焦点数量，减轻作战人员面临的作战压力，提高作战人员歼灭敌方目标的作战效率，需要在态势显控系统中对关键事件进行高优先级处理，即通过关键事件觉察，将最重要的战斗情况在态势显控界面中向作战人员直接醒目地推送和告警，使得作战人员能够快速响应战斗变化。

1 网络化火控系统中的事件

在装甲车辆网络化火控系统的态势显控技术研究中，事件是指装甲车辆分队在战斗对抗过程中动态发生的某种情况，包含两层含义：

1）敌我双方或战场环境的某种属性值突变，如装甲车辆的机动、行军路上的障碍、敌方目标出现等；

2）装甲车辆间相互关系的改变，如敌方装甲车辆进入我方装甲车辆射程等。

按照事件重要程度，事件可分为基本事件和关键事件两大类型。基本事件指作战车辆发生的基本动作，如装甲车辆出现、装甲车辆消失、装甲车辆机动（驶近、驶离、转弯…）等。关键事件指重要决策或重要目标的动态变化，以及敌方一定意图的序贯行动［1-5］。

2 关键事件察觉模型

关键事件觉察指对与敌方目标有关的关键事件进行判断与分析的过程。可分为关键事件感知和关键事件预测。关键事件感知就是将当前事件与历史事件模式类特征模板进行比较、分析、判断，从而提取出所关心的关键事件，如：发现高威胁等级目标。关键事件预测是对即将发生的敌方战术意图变化进行预测。以文献［1］提出的态势察觉模型为基础，得到关键事件觉察模型：

其中，IHL表示关键事件觉察过程；XIa表示敌方目标在各个时刻的属性信息及行为信息，一般由火控信息融合结果给出，XIa可表示为：

式（3）中，T表示采集到该批目标数据的时间；N表示目标批号，即目标的唯一标识符；E表示实体类型，如主战坦克、步兵战车等；L表示目标的空间位置；St表示目标状态，包括目标的速度和加速度矢量；W表示目标的武器载荷。

3 SVM察觉威胁等级方法

敌方高威胁等级目标或重要价值目标出现是网络化火控系统最常见的事件类型之一。一般而言，威胁度的计算会考虑敌方的位置、速度、航向、类型、射程等各因素，采用归一化方法进行归一化处理，并采用AHP模型计算各要素权值，最后进行累加得到一个0到1之间的小数，数值越大，则威胁度越大。这种方法突出的优点是计算简单，且能较好地反应敌方对我方的威胁程度。但在态势显控系统中，由于威胁度数值一直在快速变化，如果直接将威胁度的数值标识出来，可能会导致作战人员陷入大量的数据流中，无法获得真正有用的作战信息。采用支持向量机（Support Vector Machine，SVM）分类的方法将威胁等级分类，能直观地反映出目标的威胁程度，态势显控系统可以方便地将威胁等级转化为人能直观处理的事件信息，使得作战人员能够快速响应作战态势的变化［6-12］。

SVM是一种机器学习的分类模型，其基本思想是建立一个分类超平面作为决策曲面，使得正例和反例之间的隔离边缘最大化，广泛被应用与模式分类和非线性回归。

3.1 SVM原理

SVM是由线性可分模式的最优分类超平面发展而来的，对于一个线性可分的样本集，它满足：

满足式（4）且最小化权值向量w的欧几里得范数的平面成为最优分类超平面，这是一个二次约束优化问题，它的最优解由拉格朗日函数的鞍点决定：

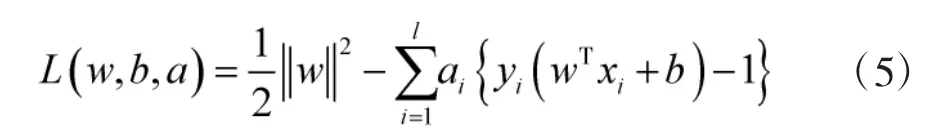
其中，辅助非负变量ai称为拉格朗日乘子，最优分类平面问题可以变形为下面的优化问题：

式（6）可以进一步变形为优化下面目标函数的拉格朗日乘子ai：

惩罚参数C是事先确定好的一个常量，用于控制目标函数中的两项，即“寻找margin最大的超平面”和“保证数据点偏差量最小”之间的权重。这个二次优化问题有唯一解，其中非零的拉格朗日乘子表示为符合的样本称为支持向量，最后得到最优分类函数f（x）：

在线性不可分的情况下，SVM采用核方法首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上不好分的非线性数据分开。引入核方法的式（7）变为：

k（x，xi）表示核函数，g表示核函数参数。常见的核函数如表1所示。

表1 常见核函数

图1 核函数功能示意图

对式（9）利用序列最小最优（Sequential Minimal Optimization，SMO）算法进行循环迭代求解，这个过程即SVM的训练过程。有上述推导过程可知，c和g是决定SVM分类效果的关键参数。SVM最初是为二分类问题设计的，当处理多分类问题时，需要构造合适的多分类器。一般采用组合多个二分类器实现多分类器的构造。使用SVM进行分类，首先需要从原始数据里把训练集和测试集提取出来，然后进行一定的预处理，之后用训练集对SVM进行训练，最后得到的模型来预测测试集的分类标签。过程如图2所示。

图2 SVM分类流程

3.2 目标威胁等级相关数据预处理

本文采用支持向量机方法进行目标威胁等级分类。首先需要对与目标威胁相关的变量数据进行数据预处理，包括：距离、相对速度、相对航向角、我方弹药消耗量、我方当前武器线与敌我平台连线夹角与敌方武器类型。下面给出各变量的归一化预处理方法。

1）目标与我方距离的归一化函数为：

其中，Sr为我方武器的最大射程，Sb为敌方武器的最大射程，Si为敌方与我方的相对距离，C为常数，且0＜C≤0.5。当敌方最大射程大于相对距离且大于我方最大射程时，距离的归一化值为1，当敌我双方均在对方射程内，距离的归一化值为0.5，当我方最大射程大于等于相对距离且大于等于敌方最大射程时，距离的归一化值随敌我双方相对距离增大而线性减小。

2）目标与我方相对速度的归一化函数为：

其中，Vr为敌方与我方相向运动的相对速度，驶向我方时为正，离开我方时为负，琢为常数，且0≤琢≤0.5，Vmax为相对速度的最大值。当小于琢Vmax时，视为相对静止，此时，相对运动速度的归一化值为 0.5，当大于琢Vmax时，视为有相对运动，相向运动的相对速度越快，相对速度的归一化值越接近1，同向运动的相对速度越快，相对速度的归一化值越接近0。琢=0.1时，该值的归一化曲线如图3所示。

图3 相向运动的相对速度的归一化函数曲线

3）目标航向相对我方航向的夹角归一化函数为：

其中，θ是目标航向相对于我方方向的夹角。相向而行时θ=π，同向而行时θ=0。越接近于相向运动，夹角的归一化值越接近1，越接近同向运动，夹角的归一化值越接近0。该值的归一化曲线如图4所示。

图4 航向夹角的归一化函数曲线

4）我方当前消耗弹药量的归一化函数为：

其中，B是当前消耗的弹药量，Bmax是最大携弹量，为正数。越接近满弹状态，消耗弹药量的归一化值越缓慢接近于0，越接近空弹状态，消耗弹药量的归一化值越快速接近于1。=2时，该值的归一化曲线如图5所示。

图5 当前消耗弹药量的归一化曲线

5）我方当前武器线与敌我平台连线夹角的归一化函数为：

考虑我方为装甲车辆，针对我方的特点，敌方武器威力u（W）归一化为：具有穿甲能力时为1，不具有穿甲能力时为0。

3.3 目标威胁等级分类规则

考虑以下的规则，将目标的威胁等级分为4等并打上标签［Treat Label］：非常危险［4］，危险［3］，较危险［2］、不危险［1］。当出现非常危险或者危险的目标时，需要操作人员立即干预并打击该目标。

超过我方射程，且在敌方射程内时，敌方武器威力越大越危险；超过敌方射程，且在我方射程内，不危险；双方均在对方射程内，敌方武器威力越大越危险；双方均在对方射程外，不危险；敌方相对于我方的相向速度分量越大越危险；双方航向越接近，越危险；我方的弹药量越满越安全；我方武器线越靠近射击时武器线越安全。

图6 我方当前武器线与敌我平台连线夹角的归一化函数曲线

3.4 仿真分析

采用LIBSVM工具箱在Matlab环境下，对分类模型进行测试。假设我方为中型坦克，射程4500m，敌方有4种类型，分别是重型坦克、轻型装甲运输车、反坦克武器1、反坦克武器2，射程分别为5 000 m、3 000 m、4 000 m、10 000 m，敌方威胁等级分别是非常危险［4］、危险［3］、较危险［2］、不危险［1］，在12*12 km的范围内随机生成250组*4类样本数据，对其预处理并按照分类规则，人工对其打上标签。

将每类的前200组数据作为训练集（共200*4组），后50组作为测试集（共50*4组），下页表2列出了训练集中的12组数据。令惩罚参数C=2，核函数参数g=1，选用高斯核，使用训练集对SVM进行训练，并用训练好的SVM对测试集进行预测，预测的正确率为96 %（192/200），如下页图7所示。

上面使用的C和g是任意给定的，下面使用交叉验证（Cross Validation，CV）的方法选择最优的SVM参数（惩罚参数c和核函数参数g），它的基本思想是当C和g在一定范围内，将训练集分成N等分，将其中的某一部分作为测试集进行预测，其余的N-1部分作为训练集对分类器进行训练，并寻找在训练集条件下达到最高准确度的C和g参数。N=3 时，C，g在［2-10，210］范围内进行查找，交叉验证的过程如图8所示。由图8可知，最优C=12.125 7，g=0.757 86，并使用最优参数作为惩罚参数和核函数参数训练SVM，并用训练后的SVM对目标的威胁程度进行分类。

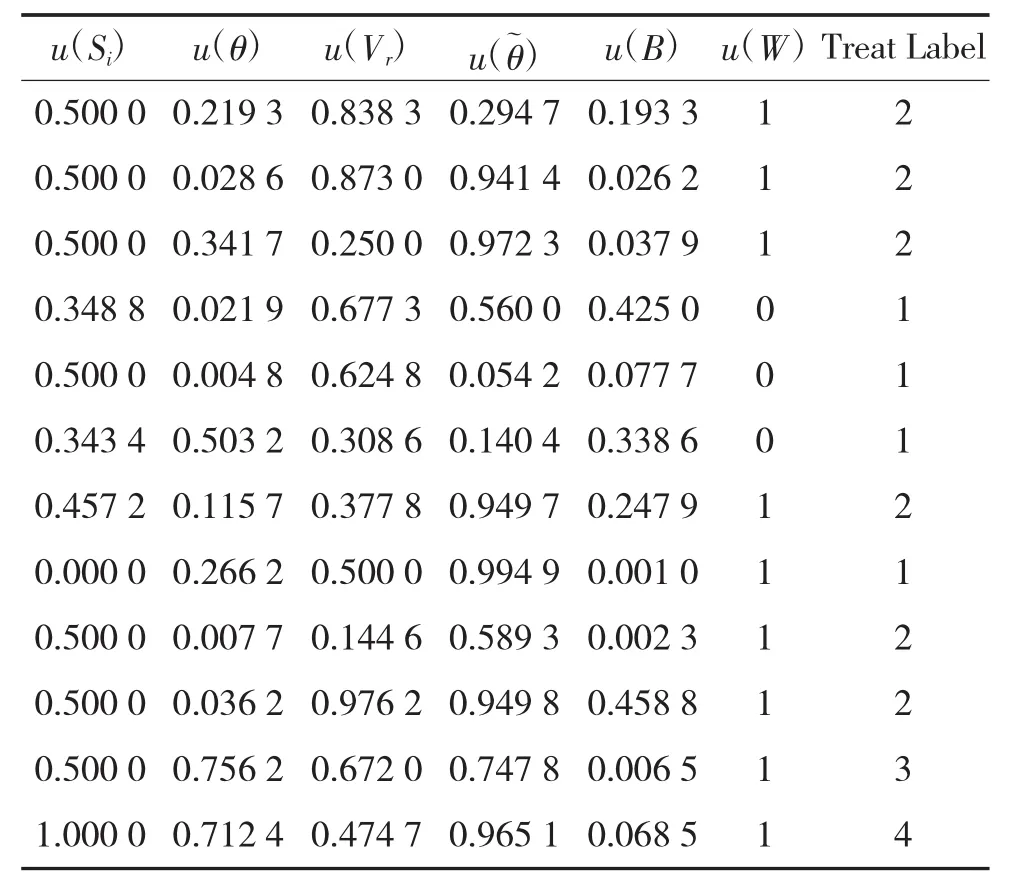
表2 参与训练的12组数据

图7 给定C=2，g=1时SVM分类结果

图8 采用交叉验证的方法寻找SVM的最优参数

仿真结果为，测试集测试SVM分类的准确率为97%（194/200）。仿真结果表明，在处理目标威胁等级分类问题时，通过对大量与目标威胁度相关的历史经验数据训练，SVM方法能够准确找到同等威胁等级数据之间的内在关系，并能够将同威胁等级的目标数据挖掘出来。因此，SVM方法是在关键事件觉察时进行目标威胁等级分类的一种有效方法，将有助坦克装甲车辆作战人员对高威胁等级的目标做出快速反应并进行打击决策。