基于任务的装甲装备器材需求预测*

王铁宁 ，杨 帆 ，吴龙涛 ，高 晟

（1.陆军装甲兵学院，北京 100072；2.解放军96163部队，江西 乐平 333300）

0 引言

传统基于任务的装甲装备器材保障中，对器材的消耗与需求规律缺乏系统、科学的掌握，因此，一般采用“尽可能多”的保障方式，即管理人员往往根据自身经验，会预先储备大量的装甲装备器材来预防短缺［1］。而实际上，过多的器材配置极容易导致库存积压，带来器材利用率低下等问题，进而导致经济效益的降低。反之，若对所需器材的数量供应不足，又会导致装备完好率降低，器材保障率不高等问题。因此，科学、准确地掌握基于任务的器材消耗规律，对装甲装备器材需求进行合理预测，是器材供应保障的核心问题，也是保证装甲装备战备完好率的重要前提。

器材需求预测作为装备保障中至关重要的一环，是器材供应与任务成功的基础。当前对器材需求预测的研究已较为成熟，但大多是基于平时训练的器材需求进行预测，因有一定的历史数据作支撑，所以常用基于统计的方法计算，例如采用时间序列法［2］、指数平滑法［3］、Croston 法［4］等，但是这些研究成果对历史数据的依赖性强，无法解决基本没有前例可循的基于任务的器材需求预测。因此，有许多专家学者针对无历史数据的器材需求进行预测，主要包括以可靠性为基础的需求预测和基于仿真的需求预测。文献［5］以可靠性为中心，按照器材一定时间内发生故障的概率，结合模糊推理机制，分别对战斗损伤和非战斗损伤引起的战时航空器材需求进行预测。文献［6］从器材故障角度考虑，分别对可修复和不可修复的航空设备器材建立需求强度的预测模型，并对由此估计的器材需求量与实际消耗量之间差值进行风险评估。文献［7］对复杂装备的相关器材建立全寿命离散仿真模型，并将仿真结果与传统需求预测模型结果进行对比，前者结果明显较优。文献［8］在分析影响器材消耗相关影响因素的前提下，对器材寿命过程进行仿真，建立器材消耗仿真模型。这些研究都为求解基于任务的装甲装备器材需求预测奠定了基础。但是另一方面，基于任务的器材需求预测，因有其自有的形式与特点，如发生时间、任务内容、任务环境等相较其他装备动用情形，都具有特殊性，因此，不能直接按照平时训练或基于战时的需求预测进行分析，必须充分考虑基于任务的特殊性，挖掘影响基于任务的器材需求预测相关因素，对装甲装备器材需求进行全面系统的研究。

本文以执行重大军事任务的装甲装备器材为研究对象，在对任务进行界定的基础上，结合影响任务器材消耗的相关因素，从器材保障成本、任务成功率与使用可用度等方面建立了基于任务的装甲装备器材需求预测模型，为任务前提下的装备保障和器材保障提供了决策支持。

1 任务及影响因素分析

1.1 任务界定

广义来讲，“任务”一般指交派的工作或承担的责任。本文中所研究的任务特指非常规训练，且非战时、非应急的重大军事行动，如抗日阅兵、出国参赛、跨区联合演习等并未在日常规划中列出，且有较充足准备时间的任务。

1.2 基于任务的器材需求影响因素分析

1）任务类型。任务的种类有许多，如出国参演、竞赛、阅兵、实战演习等。不同的任务对装备的动用要求也不尽相同，如基于阅兵任务下所动用的基本都是最新研发的、新列装部队的装备，而演习任务下所动用的往往各种类型的装备都会涵盖。动用不同类型的装备，所需的器材也会有所差别。

2）任务时长。任务时长既包括任务执行过程中从任务开始到任务结束的时间，也包括任务准备阶段，即从接到任务到任务开始的时间。任务时间越长，装备动用的摩托小时也越多，所需的器材数量也会随之增加。

3）动用装备数量。任务中动用装备数量的大小会直接影响装甲装备器材消耗的多少。其他条件一定的基础上，所动用装备数量越多，器材的需求量越大。

4）器材故障率。器材故障率是受器材本身材料、设计等影响，在其寿命过程中自然故障所发生的概率，是影响装甲装备器材需求的一个重要的内在因素。

5）环境应力。任务执行所在地域的湿度、温度、冲击、震动等均会对器材的寿命产生较大影响，尤其是长期处于高温、高腐蚀等环境下，装备及器材的可靠性会受到极大影响，从而对器材的需求产生影响。

由上述分析可知，影响基于任务的装甲装备器材需求预测的因素包括多个方面，每个因素的变化都可能引起器材消耗量变化。

2 基于任务的器材需求预测

2.1 问题假设

由上述对任务的剖析可知，在对装甲装备需求进行预测时，首先必须考虑其军事效益，即必须保证任务成功性，其次应在任务成功基础上，对所需器材进行合理配置，以达到降低成本，提高经济效益的目标。实际的任务过程中器材的消耗极其复杂，为了在不影响研究成果的基础上降低计算复杂度，本文作以下几点基本假设：

1）考虑任务实际，在任务下达初始阶段，即任务准备的开始时刻，装备为全新状态，或认为装备刚经过大修，这点在阅兵、参演等任务中尤其突出；

2）受任务的时效性与紧迫性等限制，在任务期间，当有器材出现故障时，统一采取换件修理的方式对装甲装备进行维修；

3）在任务过程中，同时存在修复性维修与预防性维修两种维修策略。其中预防性维修主要指固定时间间隔的定时维修，当检测出故障之后，即对器材进行更换，一般都在任务间隙或休息时间进行，而修复性维修则是在装备动用过程中器材出现故障影响装备的使用，则对该故障器材进行更换。

4）为了减少器材突然故障对任务的影响，一旦器材到达规定的寿命周期，即对其进行更换。

5）仅针对某一类型的器材进行研究，且忽略器材在不用装备之间的互换以及同一装备中器材的连接方式等。

2.2 问题分析

2.2.1 需求分析

通过上述分析可知，在任务期间，产生器材消耗的来源主要包括3个方面：一是器材到达规定的寿命时期而进行更换；二是器材在定期检测中检测出故障而进行更换；三是器材在任务期间发生故障而在定期检测中未及时发现。具体3种情形如图1所示，其中，0表示任务开始的时刻；T表示任务总时长，即任务的持续时间；TC为器材的平均寿命时间；t0为定期检测间隔时间，本文假设t0是根据TC长度所确定的一个固定值，可以被TC整除；TG表示器材从开始工作到被更换的时间。

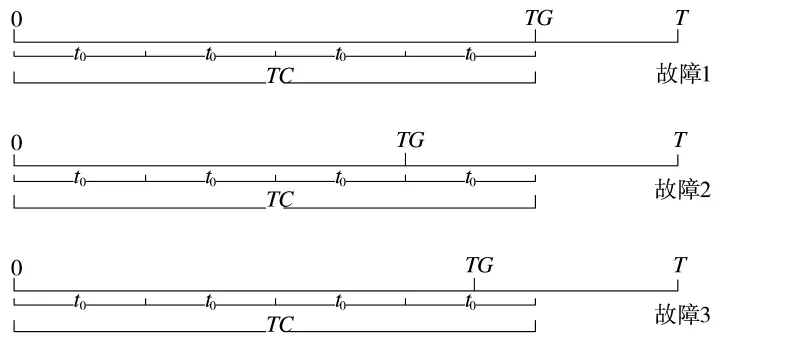
图1 3种故障情形图

下面分别对3种情况进行分析。

1）故障情形1，器材在平均寿命之前均未被检测出故障，也未发生故障，直到器材到达其平均寿命期限而被更换。可知，单次器材更换前的检测次数S1可表示为：

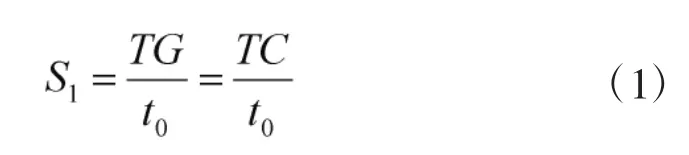
任务时间T内器材进行更换的次数G1可表示为：

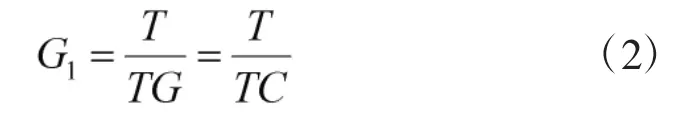
则任务期间由故障情形1产生的器材成本可表示为：

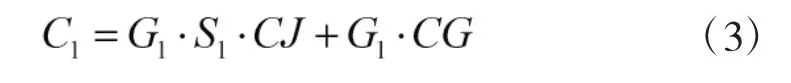
其中，C1表示故障情形1下任务期间产生的单个器材保障成本；CJ表示单次器材检测成本；CG表示单次器材更换成本。

2）故障情形2，器材未达到其平均使用寿命，但是在某次检测中发现故障而被更换。可知，单次器材更换前的检测次数S2可表示为：

任务时间T内器材进行更换的次数G2可表示为：

则任务期间由故障情形2产生的器材成本可表示为：

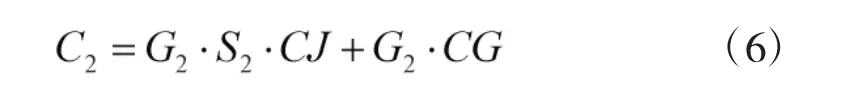
3）故障情形3，器材未达到其使用寿命，且在某两次检测间隔期发生故障而被更换。可知，单次器材更换前的检测次数S3可表示为：

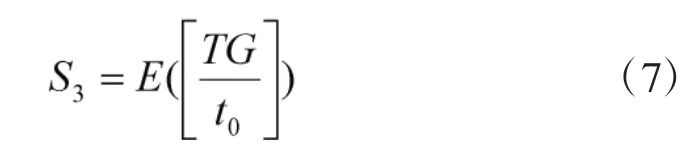
任务时间T内器材进行更换的次数G3可表示为：

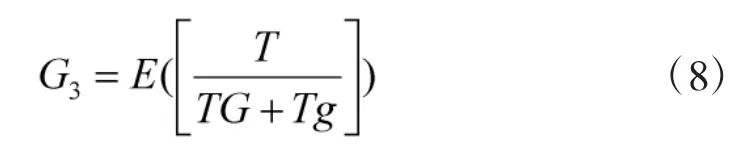
其中，Tg表示器材的故障后更换时间，认为其服从β分布，其均值与方差可分别为：

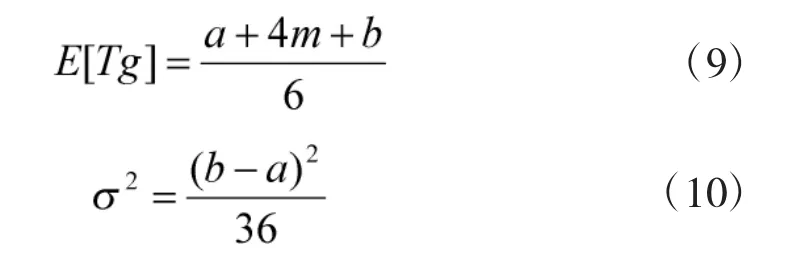
其中，a、m、b分别表示器材的维修时间最优值、最可能值与最差值。则任务期间由故障情形3产生的器材成本可表示为：

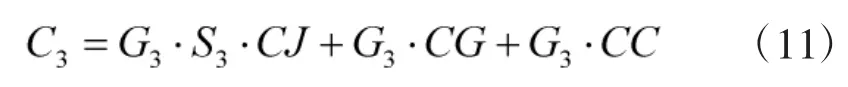
其中，［］表示取整；CC表示单次惩罚成本。因为此种故障情形一般发生在任务执行期间，往往会对任务的成功产生一定的负面影响，因此，需要引入惩罚成本。

2.2.2 参数分析

设器材的故障概率密度函数为f（t），表示在某个时间之前器材不会发生故障，而在某个时间段内发生故障的概率；可靠度函数为R（t），表示器材在规定时间内完成规定功能的概率，则器材的期望寿命可表示为：

情形2中故障在第i+1个检测点发生，可认为其在it0未发生故障，而在其后瞬时发生故障，可表示为如下条件概率［14］：

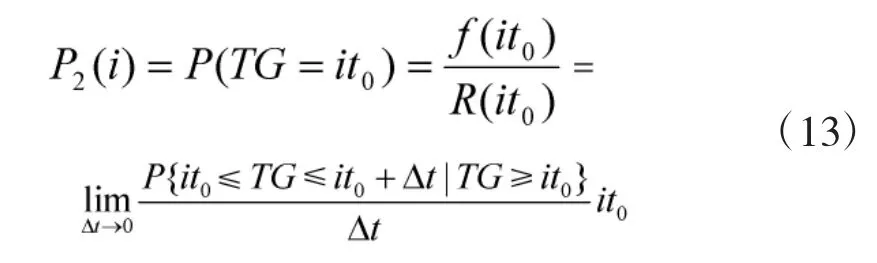
其中，f（it0）为 it0时刻的故障概率密度，R（it0）为其对应的器材可靠度函数。器材在第i个检测周期内发生故障的概率可表示为：

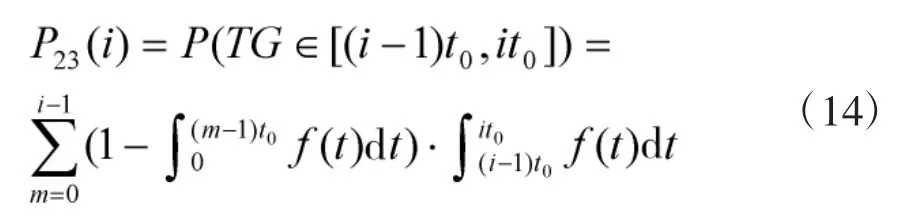
实际上，由式（14）所计算出的概率也已将式（13）情况包含在内，因此，故障情形3中器材故障概率为：

2.2 模型构建

1）目标函数。本文所分析的器材需求是基于任务成功的基础上进行的，同时兼顾其经济效益，引入任务环境影响，因此，目标函数为：

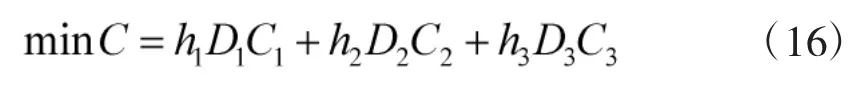
其中，h1、h2、h3为环境应力分别对3种情形的影响参数；D1、D2、D3分别表示所动用装甲装备3种情形对应装备台数，D表示任务期间装备动用总台数，则：。

2）任务成功率约束。任务成功性是衡量任务成功与否的重要指标，指从任务的开始时刻起，到任务终止过程中，装甲装备能够在规定时间内完成规定任务的能力［9，12-13］。任务成功性一般用任务成功率PC衡量。而任务可靠性［10］是指装甲装备在规定任务剖面内完成规定功能的能力，即任务期间不发生影响任务完成的故障概率。一般（0，t）时间范围内任务可靠性用任务可靠度RK（t）来衡量。则任务成功率PC与任务可靠度RK（t）的关系可表示为：

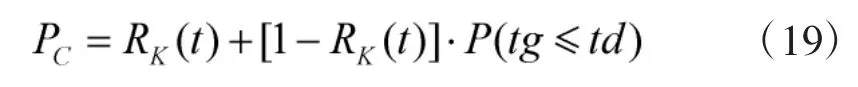
其中，tg表示装甲装备出现故障后进行修复的时间，需要注意的是表示允许装甲装备暂停动用进行修复的时间。则表示在允许时间内恢复装备执行任务能力的概率，该概率函数也称作装甲装备的维修度函数，记为，其对应概率密度函数为m（tg），表示单位时间内装甲装备在预期时间内完成维修的概率，其分布常为指数分布、正态分布等。由于本文研究对象仅考虑单种器材，因此，可认为，其中Rn（t）表示第n台装备中器材的可靠度函数。任务期间，要求任务成功率必须达到规定的目标，即PC≥PC，带入式（19）可得任务成功率约束为：

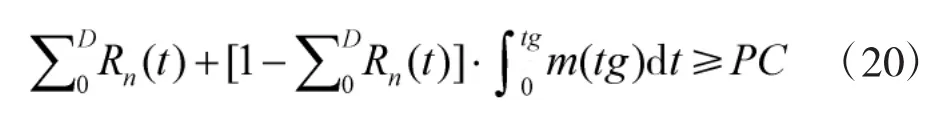
3）使用可用度约束。器材的使用可用度表示器材可工作时间与总任务时长的比值，可表示为：

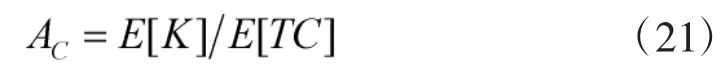
其中，E［K］表示器材工作时间的期望值，E［TC］表示器材的寿命期望值。由于本文中定期检测过程均在任务间隙完成，因此，对任务而言，器材检修时间可以忽略，则

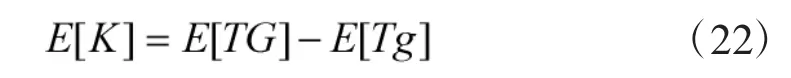
任务期间，要求器材使用可用度必须达到规定的目标，即AC≥AC，带入公式可得使用启用度约束为：

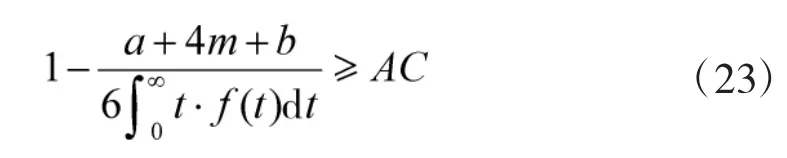
4）基于任务的装甲装备器材预测模型。综上可得如下所示的基于任务的装甲装备器材预测模型：

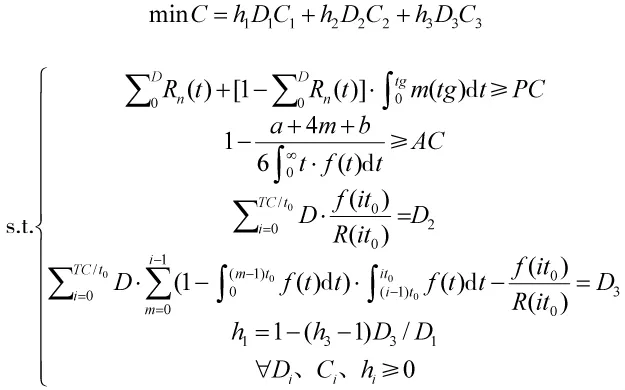
3 算例分析

本文以某次联合演习任务为研究对象，根据上述模型对其任务期间某种器材的消耗数量进行实例求解与分析。已知该次任务的总时长T=360天，装备动用总数D=50台，该种器材寿命服从参数为（4，1 000，0）的威布尔分布，其故障概率密度分布函数为［11］：

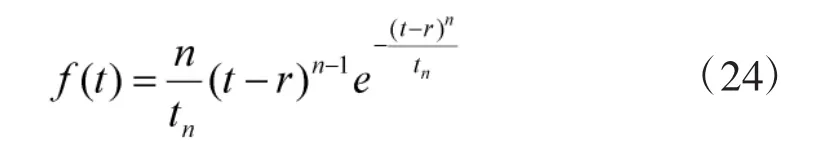
其中，n=4为威布尔分布的形状参数，tn为尺度参数，为真尺度参数，t=0为位置参数。可得到其可靠度函数，则可以求得其平均寿命：

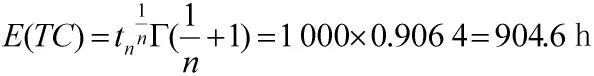
设t0为器材平均寿命的0.05倍，即t0=45.32 h。已知对于某型装甲装备的部件上该种器材发生故障的单次检测成本为80元，单次更换成本为500元，单次惩罚成本为6 000元，器材故障更换时间服从 a=20 h、m=30 h、b=40 h，则 E［Tg］=30 h。已知规定的任务成功率PC=0.95，规定器材使用可用度下限为AC=0.9。设当前环境为严寒地区，环境应力参数h2=1、h3=1.5，表示任务环境为正常环境严酷度的1.5倍，此时故障3发生概率相应增加1.5倍，为保证装备动用总数不变，h1要通过计算得出。对模型求解可得：

利用AnyLogic软件进行智能体仿真建模，对模型环境应力参数进行修正，其仿真试验如下图，其中图2表示以往任务中不同环境下器材需求量的变化，横坐标表示环境应力百分数值，纵坐标表示器材消耗数。图3表示仿真实验中的校准图，图4为历史数据与最优值的对比图。

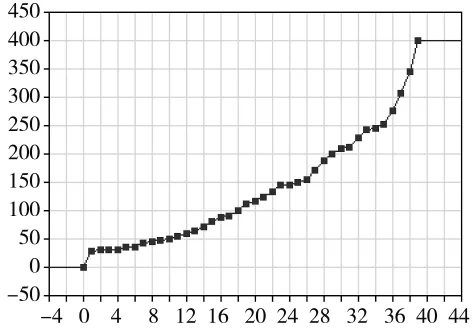
图2 环境影响历史数据

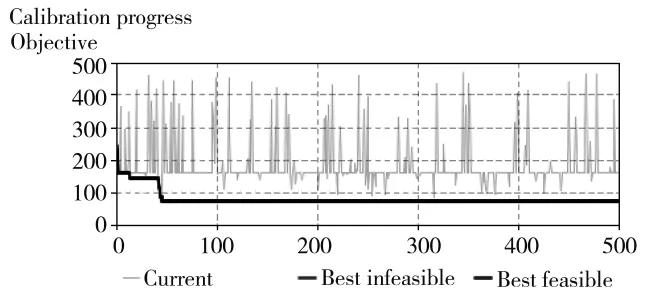
图3 仿真实验校准图

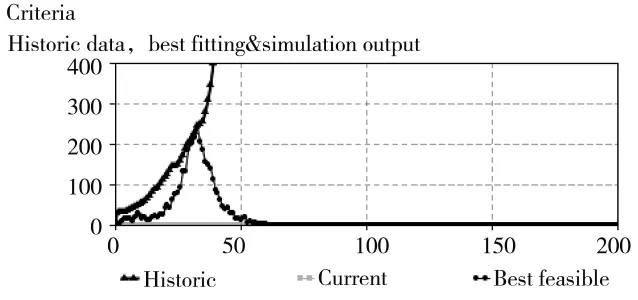
图4 仿真实验比较图

校正后参数h2=1、h3=1.59，表示其他条件固定情况下，任务环境为正常环境1.5倍时，故障发生概率为正常环境下1.59倍，h1=0.258。对动用装备数量及器材数量取整，D1=16，D2=13，D3=21，最终可得任务持续过程中该类器材消耗数Q=746个，器材保障总成本C=165 837.678元。

4 结论

本文在对任务进行剖析的基础上，分析影响任务期间器材消耗的影响因素，综合考虑各个方面，建立基于任务的器材消耗模型，并对其进行求解与仿真实验校正，为基于任务环境下的器材合理、科学配置奠定基础。实际中，对于不同类型的任务，其装备动用情况及器材消耗规律也不尽相同。而本文仅以演习任务为例进行研究，未对任务类型进行区别对待，下一步研究中，需要在本文基础上对器材需求模型进行进一步的拓展和深入。