节理岩体脆性破坏过程的有限元模拟

陈俊宇，佘成学

(武汉大学 水资源与水电工程科学国家重点实验室, 湖北 武汉 430072)

在复杂的地质条件下，天然岩体受到各种构造作用，其内部会产生大量的贯通节理。节理的存在会影响岩体的力学行为，同时降低岩体的强度[1-3]。当节理岩体的应力达到强度极限后，随着变形的增加，其强度会逐渐降低到一个较低的水平，此即节理岩体破坏后的应变软化现象[4]。其中一些节理岩体的软化速率非常大，其软化过程在应力-应变曲线中表现为一个很陡的峰后应力下降段。对于此类节理岩体，可将其破坏后的软化现象做近似处理，考虑为脆性破坏。

观察节理岩体破坏后的物理状态，发现其破坏模式并不唯一，可能因岩块破坏导致整体破碎；也可能仅仅沿着节理面变形破坏[5]。在以往的研究中，郑宏等[6]通过拓展经典塑性理论，提出了脆塑性的岩块和单结构面的应力跌落方式，但对于包含节理面的脆性岩体，并未在其变形破坏的模拟方法上展开研究。此外，朱泽奇等[7]建立了改进的层状岩体遍布节理模型。金华等[8]建立了含多组贯穿节理的扩展遍布节理岩体模型，这些模型是基于理想弹塑性理论提出，不能模拟节理岩体的软化破坏现象。朱道建等[9]引入软化参数来描述节理岩体的软化特性曲线，但在软化曲线的确定方式上缺乏理论依据。同时，上述的多种节理岩体模型对材料屈服后的应力修正方式也过于繁琐复杂，其理论有待进一步完善。

本文将节理岩体概化为一种复合材料[10]，分析节理岩体的变形破坏模式，基于弹塑性理论提出一种模拟其脆性破坏全过程的有限元方法，并利用ABAQUS编写计算子程序。利用该模型模拟青松电站引水隧洞的开挖，证明所建模型可以运用于实际工程，能较好反映脆性节理岩体的变形与破坏；用该方法可以正确模拟隧洞开挖后围岩的屈服破坏情况，验证了薄弱节理面对节理岩体的屈服破坏的重大影响。

1 节理岩体的脆性破坏模型

1.1 对节理岩体复合材料的基本假定

节理岩体由岩块和无厚度的节理面组成。岩块为各向同性体，应力-应变关系在各个坐标系中都相同；节理有对应的局部坐标系n-r-s，n为节理面外法线方向，r、s在面内相互正交，分别沿节理的走向和倾向。面上有垂直于面的法向应力σn，和在面内相互正交的两个剪切应力τnr、τns。以层状节理岩体为例，岩体与节理面的关系见图1。

图1节理岩体与节理面的关系

假定岩块和节理面为串联关系，则二者在整体坐标系中承担的荷载{σ}相等，节理岩体的总应变{ε}等于岩块与节理面的应变之和[11]，即

{σ}={σR}={σJ}

(1)

{ε}={εR}={εJ}

(2)

式中：{σR}、{εR}分别为岩块在整体坐标系下的应力和应变；{σJ}、{εJ}分别为节理在整体坐标系下的应力和应变。上标R表示岩块，上标J表示节理，大写表示整体坐标系。

节理面局部坐标系下的应力{σj}和应变{εj}可由整体坐标系转换得到，根据整体坐标系与局部坐标系的关系[12]，有

{σj}=[Tσ]{σJ}

(3)

{εj}=[Tε]{εJ}

(4)

式中：[Tσ]、[Tε]分别为应力转换矩阵和为应变转换矩阵，小写的上标j表示在局部坐标系下的节理。

1.2 节理岩体的变形破坏模式及过程分析

1.2.1 岩块与节理的变形破坏概化模型分析

脆性节理岩体包含岩块和节理两种材料，二者都可能发生破坏，其变形破坏过程对应的应力-应变曲线如图2所示。

根据图2可将岩块和节理的变形破坏过程概化为：材料由弹性状态加载到峰值强度后，发生脆性破坏并产生塑性变形，应力迅速跌落至残余强度。

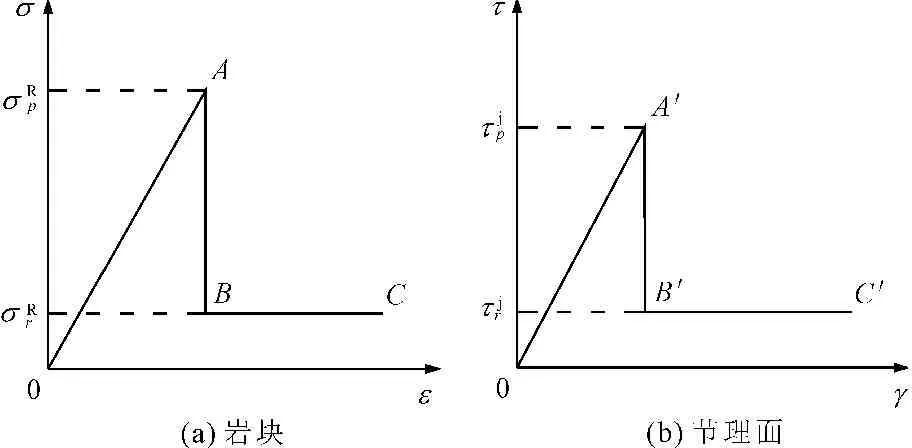
图2脆性体变形破坏应力-应变曲线简图

其中岩块采用D-P屈服准则进行描述：

(5)

节理面采用去张拉强度的M-C屈服准则进行描述：

(6)

式中：σt为节理的法向抗拉强度；α、K、φ、c为材料的力学参数。

1.2.2 节理岩体的破坏模式分析

从上述岩块和节理的变形破坏概化模型可以看出，岩块和节理的峰值强度并不一致，所以在节理岩体中，两者不一定同步破坏，由此节理岩体会呈现下列几种破坏模式：

(1) 岩块破坏而节理未破坏。由于岩块破坏后，节理不可能仍以原来的完整状态存在，必然受到岩块的影响，因此本文假定岩块破坏后节理也相应破坏。即岩块破坏后，节理随着岩块一起进入残余强度阶段。

(2) 节理破坏而岩块未破坏。节理破坏后，若岩块仍保持完好，则岩块的力学性能不受节理影响。即节理破坏而岩块未破坏时，仅节理进入残余强度阶段。

(3) 岩块与节理同时破坏。同理，受岩块破坏的影响，节理不可能以原来的完整状态存在。岩块与节理都进入残余强度阶段。

1.2.3 节理岩体的变形破坏过程分析

由于在节理岩体中岩块与节理面不一定同时破坏，且两者的弹塑性状态相互独立，所以其中一种材料还处于弹性状态时，另一种材料的应力可能已达到峰值强度而发生脆性破坏[13]。

现将节理岩体的变形破坏过程划为破坏前—应力跌落—残余强度三个阶段：

(1) 节理岩体破坏前，岩块与节理都处于弹性状态；

(2) 若岩块或节理发生脆性破坏，或两者同时破坏，称该阶段为节理岩体的应力跌落阶段；

(3) 应力跌落阶段结束后，称之为节理岩体的残余强度阶段。

1.3 节理岩体变形破坏全过程的本构关系

1.3.1 破坏前的节理岩体本构关系

{ΔσR}和{ΔεR}分别为岩块在整体坐标系下的应力、应变增量，{ΔσJ}和{ΔεJ}分别为节理在整体坐标系下的应力、应变增量，有

(7)

(8)

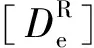
节理岩体在整体坐标系下的应力、应变增量分别为{Δσ}和{Δε}，根据上文对节理岩体复合材料的基本假定，得到

(9)

综上，记[De]为节理岩体的总体弹性矩阵，得到节理岩体在破坏前的本构关系可统一表示为

{Δσ}=[De]{Δε}

(10)

(11)

1.3.2 应力跌落阶段的节理岩体本构关系

应力跌落计算引用郑宏等[6]提出的方法：采用关联流动法则，岩块或节理在跌落过程中总应变保持不变，势函数的非连续变化导致产生非微分量的塑性应变增量，其与弹性应变增量之和为0。

对应三种破坏模式，在应力跌落阶段，节理岩体的本构关系如下：

(1) 岩块破坏而节理未破坏。跌落时的应力增量由岩块产生，节理岩体的本构关系为

(12)

式中：ΔλR为岩块的塑性跌落因子，其计算方法参见郑宏等[6]的文献。

(2) 节理破坏而岩块未破坏。跌落时的应力增量由节理产生，先在局部坐标系中计算，再转换到整体坐标系中，得到节理岩体的本构关系为

(13)

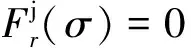
若节理压剪破坏，有

(14)

若节理张拉破坏，有

Δλj=σt/(Knd)

(15)

式中：φp和φr分别是节理的峰值内摩擦角和残余内摩擦角；Ks、Kn分别是节理的切向刚度和法向刚度；σt为节理法向抗拉强度；d为节理间距。

(3) 岩块与节理同时破坏。此时岩块和节理都会应力跌落，将跌落时的应力增量叠加，得到节理岩体的本构关系为

(16)

1.3.3 残余强度阶段的节理岩体本构关系

岩块或节理面破坏后，采用理想弹塑性屈服准则进行描述。若岩块发生破坏，则岩块改用其残余强度对应的力学参数。节理若发生压剪破坏，则改用其残余强度对应的切向力学参数；若发生张拉破坏，则改用其残余强度对应的法向力学参数。

根据上文对节理岩体复合材料的基本假定，若岩块或节理产生塑性变形，则将对应的弹性矩阵改为弹塑性矩阵，显然式(9)与式(10)、式(11)仍然成立。

记节理岩体的总体弹塑性矩阵为[Dep]，则在残余强度阶段，节理岩体的本构关系可统一表示为：

{Δσ}=[Dep]{Δε}

(17)

(18)

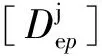
2 节理岩体脆性破坏全过程的有限元模拟

本文针对所建立的节理岩体概化模型，利用有限元软件ABAQUS进行二次开发，采用FORTRAN语言编写UMAT计算子程序，实现对节理岩体变形破坏全过程的模拟。子程序计算流程如下：

分别计算岩块和节理的试探应力，代入各自的屈服条件式判定弹塑性状态。若两种材料都处于弹性状态，则应力无需调整。若某种材料的应力已达到峰值强度，则进行应力跌落计算，再结合残余强度参数判断其弹塑性状态，进行应力修正并计算弹塑性矩阵，进而求出总体弹塑性矩阵并更新应力。最后将总体弹塑性矩阵作为雅可比矩阵，与整体应力一起返回给主程序，子程序退出。

3 工程实例

青松引水隧洞[15]通过地区属于凉山中高山区，隧洞全长近14 km。本文选取桩号4+900的断面为代表性断面进行三维有限元计算。该断面所对应洞段围岩为砂岩，属于硬岩，完整性较好；局部节理发育，一组节理与洞线大角度相交，交角取53°，倾角为41°。洞段最大埋深约1 000 m，存在较高的地应力场，垂直应力最大为26.5 MPa。

隧洞设计断面为圆形，直径5.08 m，计算时一次开挖。隧洞模型的上下左右各取50 m围岩，沿隧洞线路方向取10 m长度。围岩的左、右侧边界和沿隧洞线路方向采用水平向单链杆约束，模型底面施加垂直向约束，顶部则视为自由边界，但需考虑其上部岩体的压力作用。

有限元网格采用8节点等参单元，共计18 780个单元，22 854个节点，具体的模型网格见图3。在整体坐标系中，Y轴正向为从上游向下游沿隧洞方向，Z轴正向为垂直向上方向，X轴正向以右手法则确定。令岩块和节理的内摩擦角在硬化过程中保持不变，节理岩体的力学参数见表1和表2。

图3 隧洞模型有限元网格

表2 隧洞模型节理力学参数

开挖前先计算初始地应力场，并进行地应力平衡。隧洞开挖后，围岩受到地应力释放荷载作用，向洞内变形。

由于硬岩岩块的强度较高，开挖完成后围岩中的完整岩块基本没有屈服。但由于岩体中存在大量的薄弱节理面，因而在隧洞顶部和底部仍然有部分岩体发生屈服破坏，其破坏模式以沿节理倾向的滑移为主。围岩的屈服区分布见图4，由于节理走向与洞线斜交，屈服区左右分布不对称。

图4围岩屈服区分布

图5给出隧洞开挖后围岩的合位移增量等值线图和位移矢量图。从图5中可看到，隧洞开挖后围岩向洞内变形，洞顶及洞底的位移增量最大，最大值为2.95 cm。同样由于节理走向与洞线斜交，位移增量的左右分布不对称。由于隧洞开挖后围岩中岩块仍处于弹性状态，岩体变形不大，能保持稳定。

图5围岩的位移分布

计算中以拉应力为正，压应力为负，隧洞开挖后围岩中的应力以压力为主，图6给出围岩的最小主应力等值线分布图。从图6中可看出，受薄弱节理面的影响，隧洞开挖后，洞顶及洞底周围部分岩体发生屈服破坏，导致这两处围岩的主应力值较小。围岩的最大压应力数值约63.93 MPa，位于隧洞洞腰处中。同样由于节理走向与洞线斜交，应力的左右分布不对称。

图6围岩的最小主应力分布

综合上述计算结果，表明对于强度很高的硬岩，若其中有薄弱节理面存在，则隧洞开挖时围岩的变形破坏主要由节理所控制。围岩容易沿节理发生剪切错动，导致围岩变形不断增大，最终发生屈服破坏[16]。实际工程中，考虑脆性破坏的节理岩体能很好反映自身的变形破坏情况。

4 结 论

(1) 将节理岩体概化为连续复合材料，分析脆性节理岩体的三种破坏模式。根据各破坏模式分别建立对应的节理岩体变形破坏本构关系。基于弹塑性理论得到节理岩体的应力修正方法，提高了计算效率。基于ABAQUS编写UMAT计算子程序，实现对节理岩体变形破坏全过程的模拟。

(2) 对青松引水隧洞的开挖过程进行数值模拟，证明了本文的理论模型可运用于实际工程，用该方法能较好地模拟脆性节理岩体的变形与破坏，正确反映隧洞开挖后围岩的屈服破坏情况。

(3) 通过计算结果得出，在强度较高的硬岩中，围岩的破坏主要是由节理破坏所导致，同时表明薄弱节理面对节理岩体的位移、应力，和屈服破坏都有重大影响。